Open Journal of Inorganic Chemistry
Vol.3 No.2(2013), Article ID:30857,7 pages DOI:10.4236/ojic.2013.32007
Thermally induced gelation of alumina shaping-neutron scattering and rheological measurements
![]()
1Centre for Ceramic Processing, International Advanced Research Centre for Powder Metallurgy and New Materials, Hyderabad, India
2Solid State Physics Division, Bhabha Atomic Research Centre, Trombay, India
Email: *royjohnson@arci.res.in
Copyright © 2013 Papiya Biswas et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 15 February 2013; revised 18 March 2013; accepted 29 March 2013
Keywords: Ceramics; Polymers; Heat Treatment; Molecular Dynamics
ABSTRACT
Thermally induced gelation forming based on methylcellulose is recently being explored as a simple and environmentally benign process. Alumina slurry containing 0.1 wt% methylcellulose is subjected to Quasi Elastic Neutron Scattering (QENS) and rheological measurements in gelation temperature regimes to evolve a possible mechanism of the forming process. A reduction in diffusivity of water in the slurry from 2.16 to 1.92 × 10−5 cm2∙s−1 after exposure to 55˚C is observed with QENS. This is found to be well correlated with a steep increase in viscosity from 1.2 Pa.s till 50˚C to 50,000 Pa.s at 55˚C. QENS studies revealed the diffusion of water occurs by jump diffusion with the jump lengths distributed randomly. Further, for the entire sample much longer residence time is found as compared to bulk water, which is due to hydrophilic interaction of water molecules with the methylcellulose in the slurry. Reduction in diffusivity of water along with the steep increase in viscosity could be understood as the strong, cross-linked polymer-solvent irreversible gel formation in presence of alumina which is responsible for the retention of a consolidated shape of the ceramic green body. Samples maintained the integrity while heat treatments achieving close to theoretical density values of 3.98 g∙cm−3 at 1550˚C.
1. INTRODUCTION
Methylcellulose is a water soluble organic compound with very good compatibility and solubility characteristics that makes it a choice of binder for various ceramic processing [1,2]. Methylcellulose is presently used widely for ceramic shaping by viscous plastic processing such as extrusion and injection molding [3,4]. Methylcellulose is also broadly used for the coating purpose in pharmaceutical, textile and in paper industry. Methylcellulose is composed of two components such as naturally occurring cellulose and methyl (-CH3) side groups. Cellulose itself is water insoluble, due to the intra and intermolecular hydrogen bonds. However, when a certain number of the hydroxyl groups are substituted by methoxyl groups, some of the hydrogen bonds are broken and methylcellulose becomes water soluble. The solubility is also a strong function of the degree of substitution and generally the commercial products have an intermediate degree of substitution [5]. Though methylcellulose is water soluble at lower temperatures, at elevated temperatures beyond 50˚C, hydrophobic effects manifest into gelation. Recently, this unique gelation property of methylcellulose is employed for aqueous gel casting process for slurry leading to the shaping of simple and complex shapes [6,7]. The process is proven to have advantages of defect free processing and improved densification [8]. So it is of interest to study the change in viscosity with respect to temperature and correlate with diffusion of water in alumina slurry containing the methylcellulose and after exposing the same to the gelation temperature.
Sarkar et al. [9] has studied the gelation of aqueous methylcellulose. An initial drop in viscosity observed during the study was primarily attributed to the gradual loss of water of hydration from methylcellulose. It was observed that as the temperature is increased beyond 50˚C the dehydration also increases leading to polymerpolymer interactions resulting in a network structure leading to the drastic increase in viscosity as have been observed in the viscosity versus temperature plot. The authors thus ascribed complex viscosity as a function of temperature to study the manifestation of gelation.
The effect of gelation may influence the dynamics of water in alumina slurry. Therefore, it is of interest to study the diffusion of water molecules inside alumina slurry exposed under different conditions. Diffusion of water can be studied using several experimental techniques including PFG-NMR [10] and QENS [11]. QENS, in particular, has been employed widely due to its ability to give spatial as well as temporal information on a wide range of time (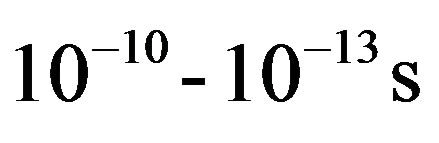 ) and length (few angstroms) scales. It is very well suited to study the diffusion in hydrogenous material such as water confined in porous media [12-18], hydrocarbons adsorbed in zeolites [19], micellar system [20] and so forth due to its large scattering cross section with hydrogen. This technique provides quantitative as well as qualitative information about the dynamics. The broadening of peaks observed over the instrumental resolution limit can be correlated to the dynamics of the system under evaluation. The quantitative information obtained from the analysis of the data entails the information about the correlation time, length scale and activation energy while qualitative information pertains to the geometrical mechanism of the motion. In a QENS experiment, information on molecular dynamics is obtained by considering the dynamical structure factor, S(Q,w), which is a measure of the probability that an incident neutron undergoes a scattering process with an atom by exchanging energy ħw and momentum ħQ. Characteristic times and the spatial extent of the molecular dynamics can be obtained by analyzing the w and Q dependence of S(Q,w) respectively.
) and length (few angstroms) scales. It is very well suited to study the diffusion in hydrogenous material such as water confined in porous media [12-18], hydrocarbons adsorbed in zeolites [19], micellar system [20] and so forth due to its large scattering cross section with hydrogen. This technique provides quantitative as well as qualitative information about the dynamics. The broadening of peaks observed over the instrumental resolution limit can be correlated to the dynamics of the system under evaluation. The quantitative information obtained from the analysis of the data entails the information about the correlation time, length scale and activation energy while qualitative information pertains to the geometrical mechanism of the motion. In a QENS experiment, information on molecular dynamics is obtained by considering the dynamical structure factor, S(Q,w), which is a measure of the probability that an incident neutron undergoes a scattering process with an atom by exchanging energy ħw and momentum ħQ. Characteristic times and the spatial extent of the molecular dynamics can be obtained by analyzing the w and Q dependence of S(Q,w) respectively.
Hence, the objective of the current work is therefore to correlate the gelation process occurring in alumina slurry by complex viscosity measurements with a function of temperature and corresponding diffusion of water by QENS. Further the gelation process was also successfully employed for colloidal shaping of alumina ceramics as a simple and environmentally benign process.
2. EXPERIMENTAL PROCEDURE
2.1. Preparation of the Slurry
High purity alumina powder (AHPA 0.5, Sasol, USA) with specifications of 99.96% purity with a BET surface area of 8 m2/g and average particle size (D50) of 0.5 μm is used in the present study. Aqueous slurry is exposed in distilled water using Darvan 821A (R. T. Vanderbilt Co., Inc., Norwalk, CT, USA) as a dispersant and milled for 4 - 5 hrs in polypropylene bottles in a pot jar mill. Thus obtained alumina slurry with >75 wt% of solid loading was further mixed with 0.1 wt% of methylcellulose (Dow Chemical Company).
2.2. Rheological Measurements
Rheological behaviour of the slurries was measured at varying shear rates (MCR 51, Anton Paar, Austria) to determine the flow properties. The variation in viscosity as a function of temperature was also studied at low shear rates of 10 s−1 in the temperature range of 25˚C - 70˚C at the heating rate of 1˚C/min.
2.3. Neutron Scattering Experiment
Neutron scattering measurements were carried out by using the QENS spectrometer at Dhruva reactor, Trombay [21] on alumina slurry samples. The alumina slurry samples, containing 0.1 wt% methylcellulose, were exposed at different temperatures of 45˚C (designated as sample #1), 50˚C (designated as sample #2) and 55˚C (designated as sample #3). In addition sample #2 is re-heated and equilibrated to 60˚C for 4 hrs and subsequent QENS data recorded at room temperature. The spectrometer is used in multi angle reflecting crystal (MARX) mode, which uses a combination of a large analyser crystal for energy analysis and a position sensitive detector for detecting the scattered neutrons. In the present configuration, this instrument has an energy resolution of 200 μeV with incident neutron energy of 5 meV as obtained from standard vanadium sample. The quasielastic data were recorded on all samples in the wave vector transfer (Q) range of 0.67 Å−1 - 1.8 Å−1 at 27˚C.
2.4. Shaping of Alumina Components
Alumina slurry containing the 0.1 wt% of methylcellulose was casted into molds as per the gelation procedure described elsewhere [8]. The samples of uniform geometry were cut from various configurations after and the green density was measured using dimensional method. The samples were heat treated without cracks at the rate of 3˚C/min during the binder burn out regime and could be sintered close to theoretical densities on sintering the samples at a peak temperature of 1550˚C.
3. RESULTS AND DISCUSSIONS
3.1. Viscosity Measurements
The plot of apparent viscosity with shear rate for alumina slurry containing the 0.1 wt% of methylcellulose is shown in Figure 1(a). It is evident that the as received slurries are pseudo plastic at lower shear rates and as the shear rate is increased beyond 200 s−1 the slurries exhibit close to Newtonian behavior. The change in the complex viscosity with respect to temperature is shown in Figure 1(b). In the case of alumina slurry with 0.1 wt% concentration of methylcellulose the slurry had an initial viscosity of 1.2 Pa.s at room temperature. The viscosity remains
 (a)
(a) (b)
(b)
Figure 1. Plots of (a) viscosity with shear rates for the alumina slurry and (b) complex viscosity versus temperature for alumina slurry.
unchanged or with marginal decrease till the slurry reaches a temperature of 50˚C which demonstrated a very prominent increase (Figure 1(b)) in viscosity to 50,000 Pa.s revealing the gelation.
3.2. Quasi elastic Neutron Scattering Measurements
In a neutron scattering experiment the scattered intensity is analyzed as a function of both energy and momentum transfer. The quantity measured is the double differential scattering cross section representing the probability that a neutron is scattered with energy change dE = ħdω into the solid angle dW [12],
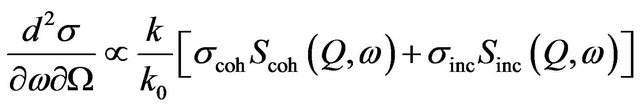 (1)
(1)
where σ is the scattering cross-section, subscripts coh and inc denote the coherent and incoherent components and S(Q,w) is the scattering law. k and k0 are the final and initial wave vectors. Q = k − k0 is the wave vector transfer [Q = 4p sinq/l, where 2q is the scattering angle in case of elastic scattering] and ћω = E − E0 is the energy transfer. For systems containing hydrogen atoms as σcoh (any element) << σinc (hydrogen), one can write,
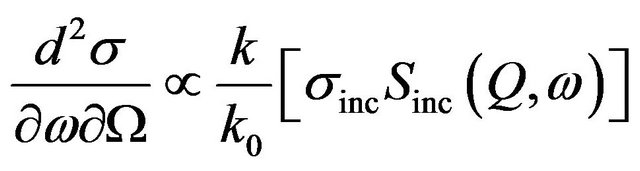 (2)
(2)
Therefore, in a neutron scattering experiment from the alumina slurry the observed dynamics mainly corresponds to the self-correlation function of the protons . In general, this scattering law can be written as [12]
. In general, this scattering law can be written as [12]
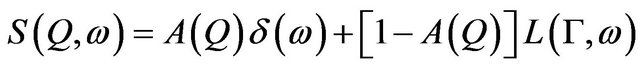 (3)
(3)
where the first term is the elastic part and the second is the quasielastic one. L(G,w) is a Lorentzian function with a half width at half maxima (HWHM) G. The variation of HWHM, G provides information about the time scale of the motion. The contribution of the elastic scattering out of total scattered spectra is called the Elastic Incoherent Structure Factor (EISF). Therefore, A(Q) in Eq.3 is nothing but the EISF, which represents the space Fourier transform of the particle distribution, taken at infinite time and averaged over all the possible initial positions. A negligible contribution of EISF generally corresponds to the presence of pure long-range translational motion. However for localized motion e.g., rotational motion, this term is expected to have a non-zero value and the variation of EISF with Q is used to determine the information about the geometry of the molecular motion.
It may be noted that in a QENS experiment, the measured data is inherently convoluted with the resolution function of the instrument. To analyse the QENS data, it is customary to assume a theoretical scattering function (Eq.3), convolute with the instrumental resolution function and then obtain the dynamical parameters involved in the model scattering function by least squares fit to the experimental data.
The quasielastic spectra were recorded in the wave vector transfer (Q) range of 0.67 - 1.8 Å−1 at 27˚C for slurry samples #1, #2 and #3 i.e. exposed at 45˚C, 50˚C and 55˚C respectively. QENS measurements have been also carried out on sample #2 after exposing to 60˚C. Significant quasi-elastic broadening was observed for all the samples over the instrument resolution. Thus, this broadening is related to the dynamical motion of water molecules in the alumina slurry. It is found that the sample #1 and #2 show larger quasi elastic (QE) broadening compared to sample #3, that is, the slurry exposed at 55˚C. However, QE broadening in samples #1 and #2, that is, slurry exposed at 45˚C and 50˚C are found to be similar. This indicates qualitatively that diffusivity of water in slurry exposed at 45˚C and 50˚C is very similar however different than slurry exposed at 55˚C.
This suggested that the water molecules in slurry exposed at 55˚C experience different environment while diffusing compared to that in other samples exposed at lower temperatures. Therefore, sample #2 (slurry exposed at 50˚C) is reheated to 60˚C and further QENS measurement were carried out at room temperature. It is found that after heat treatment of sample #2, observed QE broadening is reduced and found very similar to the slurry exposed at 55˚C. This suggests that after heating, slurry exposed at 50˚C manifests the same environment to water molecules as that in sample exposed at 55˚C. To extract detailed information QENS data are analysed with the model scattering law as given in Eq.3. The parameters, A(Q) and Γ(Q) were obtained by least squares fit. The resulting fits are shown in Figures 2 and 3 for all the measured samples at typical Q values.
In the present case for all the samples, the elastic intensity are found to be negligible and a single Lorentzian function is good enough to describe the data, indicating that the observed dynamics correspond to the translational diffusion of the sorbed water molecules. The simplest model of translational motion is Brownian diffusion, which is described by Fick’s law, in which HWHM (G) of the quasielastic component (Lorentzian function) varies linearly with Q2, G(Q) = DQ2, where D is the self-diffusion coefficient of fluids. This occurs when the interactions between the particles are weak. When the intermolecular interactions are significant, the diffusion mechanism deviates from the Fick’s law. Here, two characteristic times are involved with the dynamical process. These are, the jump time t1 during which the particle diffuses and the residence time t during which it undergoes oscillatory motions around any point r. Further, when jump time t1 is negligible compared to the residence time t, the corresponding diffusion mechanism is known as jump diffusion. The molecule moves in the form of discrete jumps where the molecule remains at a given site for a specific time called the residence time before jumping instantly to another site separated from the first by a distance called the jump length. It has been shown [22,23] that for an isotropic distribution of jump length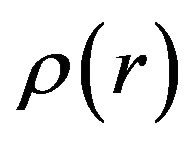 , the scattering law is a Lorentzian with a half width at half maximum (HWHM) given by
, the scattering law is a Lorentzian with a half width at half maximum (HWHM) given by
 (4)
(4)
In the case of a liquid, equipotential sites are not very well ordered as one might expect the jump length make a distribution which may be a Gaussian or random distribution. The corresponding jump diffusions are known as Hall and Ross [24] and Singwi-Sjölander [25] jump diffusions respectively. It may be noted that in all these jump diffusion models, the difference is that of a micro-
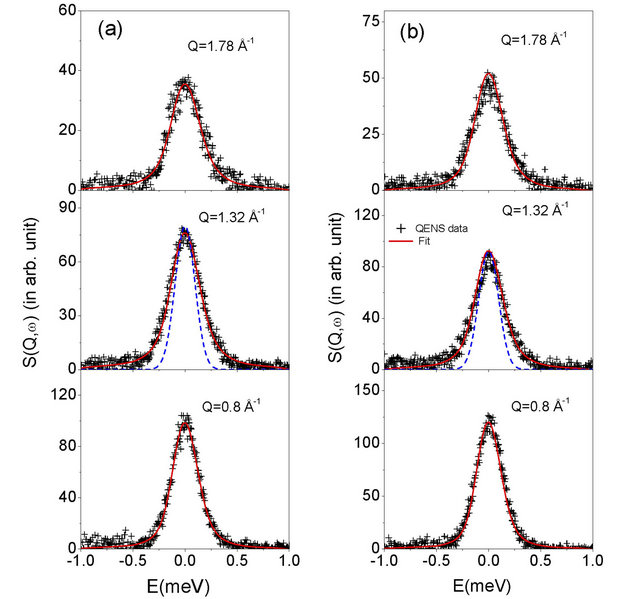
Figure 2. Fitted QENS spectra measured at room temperature from 0.1 wt% methylcellulose-alumina slurry samples exposed at 50˚C (sample #2) (a) before exposing to high temperature (b) and after exposing to 60˚C, at some typical Q values. Instrument resolution is shown by dashed line in the middle panel.
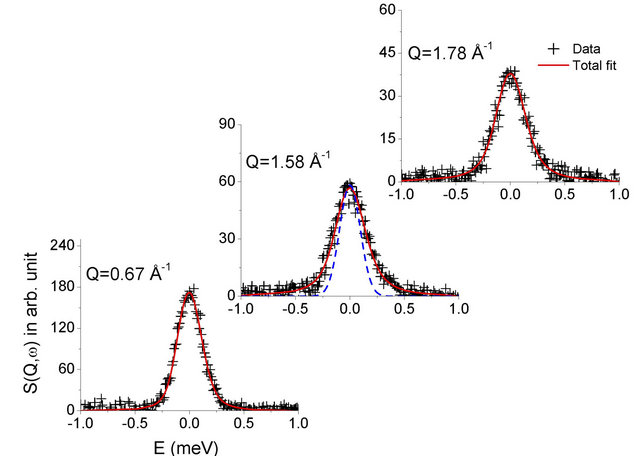
Figure 3. Fitted QENS spectra measured at room temperature from 0.1 wt% methylcellulose-alumina slurry sample exposed at 55˚C (sample #3) at some typical Q values. Instrument resolution is shown by dashed line in the middle panel.
scopic detail. In case the system is studied at a larger length scales or equivalently at smaller Q values, the information about these finer details is lost and the diffusion process looks very much like the Brownian diffusion. The variation of G(Q) with Q2 is therefore linear at low Q values and the diffusion coefficient can be obtained simply from the slope of this curve in the region of small Q values. At higher Q values however, as finer details of the jump diffusion start to emerge, the variation of G(Q) with Q2 is no more linear and tend to saturate to a value, which is indicative of the residence times involved in the jump process. In the present case for all the samples, the variation of G(Q) with Q2 obtained from the experimental data were found to be described well by the Singwi-Sjölander model of jump diffusion, which employs a random distribution of jump lengths. In this model the variation of G(Q) with Q2 is given by [25]
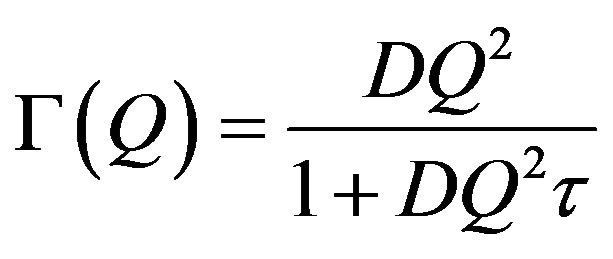 (5)
(5)
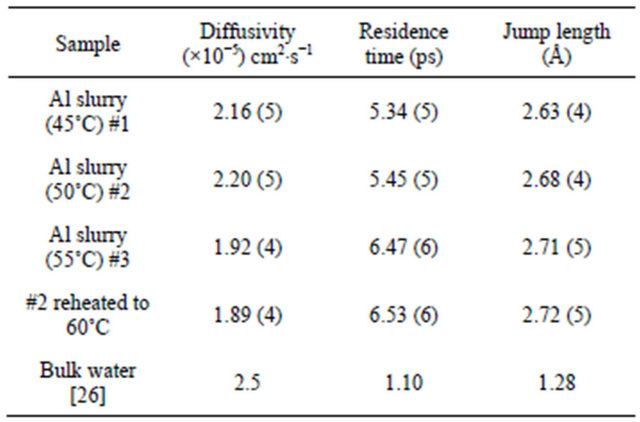
where D is the diffusion coefficient and τ is the residence time. The variation of G as obtained from the fit for both samples is plotted in Figure 4 as a function of Q2 along with the experimental values. The deviation of the graph from the linear behavior at high Q justifies the jump diffusion model. The solid line in Figure 4 corresponds to the least squares fit with the experimentally obtained values assuming Eq.5. The values of the parameters, D and τ as obtained from the fit are shown in Table 1.
Mean jump length 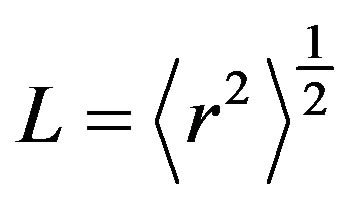 for the water in the Al slurry can be obtained using Einstein relation
for the water in the Al slurry can be obtained using Einstein relation 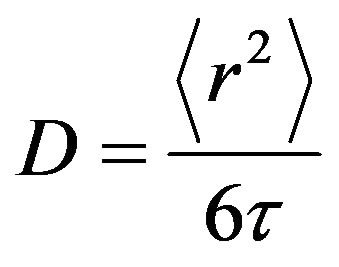
and also given in Table 1. It may be noted that the residence time obtained for sample #1 is 5.34 ps, which is much larger than that of water in bulk 1.1 ps. This is probably the result of attractive interaction of water molecules with the methylcellulose in the slurry sample, which makes the motion of water molecules hindered, thereby increasing the residence time. It is clear that diffusion of water in slurry sample exposed at 55˚C is found to be hindered than the slurry exposed at lower temperatures (45˚C and 50˚C). Residence time of water molecule is also found to be larger for slurry exposed at 55˚C. This could be interpreted in terms of restricted diffusion of water due to gelation. As the temperature increased above to 50˚C, cross-linked polymer-solvent gel formation takes place, which restrict the diffusion of water, and observed diffusivity is found to be reduced. QENS results obtained from heated (60˚C) slurry sample exposed at 50˚C (sample #2) further confirmed our interpretation. It is found that diffusivity of water in sample #2 after heating to 60˚C is found to be similar to that observed in slurry sample exposed at 55˚C. Results obtained for neutron scattering, a microscopic technique, are found to be consistent with the macroscopic viscosity measurements, which suggest that temperature beyond 50˚C increases polymerpolymer interactions resulting in a network structure.
3.3. Shaping of Alumina Components
The samples shaped by employing the gelation process with the green density values of 1.95 g∙cm−3 is shown in Figure 5(a) along with the samples sintered to 1550˚C. The sintered samples (shown in Figure 5(b)) exhibited a density close to theoretical density of 3.98 g∙cm−3, which is also complimented by microstructures depicted in Figure 5(c).
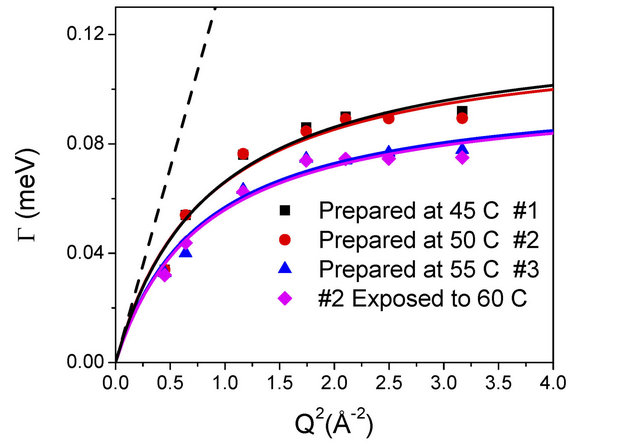
Figure 4. Variation of HWHM G, quasielastic component for 0.1 wt% methylcellulose-alumina slurry samples exposed at different temperatures with Q2. The solid line corresponds to the fit assuming random jump diffusion model whereas dashed line show as expected with Fick’s law.
Table 1. Diffusion coefficients and residence time are given for studied Al slurry samples at room temperature.
4. CONCLUSION
Thermally induced gelation process of methylcellulose, a derivative of naturally occurring cellulose has been successfully employed for the shaping of alumina parts from the slurry. Rheological and neutron scattering measurements were employed for tracking the gelation process. Rheological measurements of alumina slurry while insitu heating has exhibited a steep increase in viscosity in the temperature range of 50˚C - 55˚C. Neutron scattering studies also revealed a reduction in the diffusivity of water after exposing the sample at and above 55˚C. It is found that the water molecules in alumina slurry undergo random jump diffusion. The motion is sub-diffusive and the residence time is much longer compared to bulk water. It is found that on gelation (sample #3) the diffusion is hindered and residence time goes up which is in conjunction with the viscosity data. The jump lengths are found to be more or less similar for all the samples. It is

(a)

(b)

(c)
Figure 5. (a) Thermal gel cast green samples; (b) Sintered samples; and (c) Microstructure of sintered samples at 1550˚C.
explained that cross-linked polymer network formation is responsible for the above observed phenomena, which can also be correlated to consolidated green alumina part on casting. Sintered samples have demonstrated the density close to theoretical value in combination with a dense micro-structure confirming the possibility of defect free shaping through methylcellulose based thermally induced gel casting process.
REFERENCES
- Scheutz, J.E. (1986) Methyl cellulose polymers as binders for extrusion of ceramics. Journal of the American Ceramic Society, 88, 1556-1559.
- Lange, F.F. (1989) Powder processing science and technology for increased reliability. Journal of the American Ceramic Society, 72, 3-10. doi:10.1111/j.1151-2916.1989.tb05945.x
- Rivers, R.D. (1978) Method of injection moulding powder metal parts. US Patent 4113480.
- Bayer, R. and Knarr, M. (2012) Thermal precipitation or gelling behaviour of dissolved methyl cellulose (MC) derivatives—Behaviour in water and influence on the extrusion of ceramic paste. Part 1: Fundamental of MC derivatives. Journal of European Ceramic Society, 32, Article ID: 10071018. doi:10.1016/j.jeurceramsoc.2011.11.025
- Koda, S., Hori, T., Nomura, H. and Kawaizumi, F. (1991) Hydration of methyl cellulose. Polymer, 32, 2806-2810. doi:10.1016/0032-3861(91)90112-V
- Xu, X., Wen, Z., Lin, J., Li, N. and Wu, X. (2010) An aqueous gel-casting process for -LiAlO2 ceramics. Ceramic International, 36, 187-191. doi:10.1016/j.ceramint.2009.07.017
- Biswas, P., Swathi, M., Ramavath, P., Rajeswari, K., Suresh, M.B. and Johnson, R. (2012) Diametral deformation behaviour and machinability of methyl cellulose thermal gel cast processed alumina ceramics. Ceramic International, 38, 6115-6121. doi:10.1016/j.ceramint.2012.04.059
- Hareesh, U.S., Anantharaju, R., Biswas, P., Rajeswari, K. and Johnson, R. (2011) Colloidal shaping of alumina ceramics by thermally induced gelation of methyl cellulose. Journal of the American Ceramic Society, 94, 749-753. doi:10.1111/j.1551-2916.2010.04188.x
- Sarkar, N. and Greminger Jr., G.K. (1983) Methyl cellulose polymers as multifunctional processing aids in ceramics. American Ceramic Bulletin, 62, 1280-1284.
- Kärger, J. and Ruthven, D.M. (1992) Diffusion in zeolites and other microporous solids. Wiley Interscience, New York.
- Bée, M. (1988) Quasielastic neutron scattering. Adam Hilger, Bristol.
- Sharma, V.K., Mitra, S., Kumar, A., Yusuf, S.M., Juranyi, F. and Mukhopadhyay, R. (2011) Diffusion of water in molecular magnet Cu0.75Mn0.75[Fe(CN)6]⋅7H2O. Journal Physics: Condensed Matter, 23, 446002-446009. doi:10.1088/0953-8984/23/44/446002
- Sharma, V.K., Mitra, S., Singh, P., Jurany, F. and Mukhopadhyay, R. (2010) Diffusion of water in nano-porous polyamide membranes: Quasielastic neutron scattering study. The European Physical Journal Special Topics, 189, 217-221. doi:10.1140/epjst/e2010-01325-9
- Sharma, V.K., Singh, P.S., Gautam, S., Mitra, S. and Mukhopadhyay, R. (2009) Diffusion of water in nanoporous NF polyamide membrane. Chemical Physics Letter, 478, 56-60. doi:10.1016/j.cplett.2009.07.045
- Sharma, V.K., Singh, P.S., Gautam, S., Maheshwari, P., Dutta, D. and Mukhopadhyay, R. (2009) Dynamics of water sorbed in reverse osmosis polyamide membrane. Journal of Membrane Science, 326, 667-671. doi:10.1016/j.memsci.2008.11.003
- Mitra, S., Mukhopadhyay, R., Tsukushi, I. and Ikeda, S. (2001) Dynamics of water in confined space (porous alumina): QENS study. Journal Physics: Condensed Matter, 13, 8455-8465. doi:10.1088/0953-8984/13/37/302
- Chakrabarty, D., Gautam, S., Mitra, S., Gil, A., Vicente, M.A. and Mukhopadhyay, R. (2006) Dynamics of absorbed water in saponite clay: Neutron scattering study. Chemical Physics Letter, 426, 296-300. doi:10.1016/j.cplett.2006.05.131
- Mitra, S., Pramanik, A., Chakrabarty, D., Jurányi, F., Gautam, S. and Mukhopadhyay, R. (2007) Diffusion of water adsorbed in hydrotalcite: Neutron scattering Study. Journal of Physics: Conference Series, 92, 012167- 012171. doi:10.1088/1742-6596/92/1/012167
- Sharma, V.K., Gautam, S., Mitra, S., Rao, M.N., Tripathi, A.K., Chaplot, S.L. and Mukhopadhyay, R. (2009) Dynamics of adsorbed hydrocarbon in nanoporous zeolite framework. Journal of Physical Chemistry B, 113, 8066-8072. doi:10.1021/jp9014405
- Sharma, V.K., Mitra, S., Sakai, V.G., Hassan, P.A., Embs, J.P. and Mukhopadhyay, R. (2012) The dynamical landscape in CTAB micelles. Soft Matter, 8, 7151-1760. doi:10.1039/c2sm25515d
- Mukhopadhyay, R., Mitra, S., Paranjpe, S.K. and Dasannacharya, B.A. (2001) Quasielastic neutron scattering facility at Dhruva reactor. Nuclear Instrumentation Method A, 474, 55-66.
- Chudley, C.T. and Elliott, R.J. (1961) Neutron scattering from a liquid on a jump diffusion model. Proceedings Physics Society, 77, 353-361. doi:10.1088/0370-1328/77/2/319
- Egelstaff, P.A. (1967) An introduction to the liquid state. Academic Press, London.
- Hall, P.L. and Ross, D.K. (1981) Incoherent neutron scattering functions for random jump diffusion in bounded and infinite media. Molecular Physics, 42, 673-682. doi:10.1080/00268978100100521
- Singwi, K.S. and Sjölander, A. (1960) Diffusive motions in water and cold neutron scattering. Physical Review, 119, 863-871. doi:10.1103/PhysRev.119.863
- Tiexiera, J., Bellissent-Funel, M.C., Chen, S.H. and Dianoux, A.J. (1985) Experimental determination of the nature of diffusive motions of water molecules at low temperatures. Physical Review A, 31, 1913-1917. doi:10.1103/PhysRevA.31.1913
NOTES
*Corresponding author.

