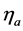Journal of Quantum Information Science
Vol.07 No.02(2017), Article ID:76394,10 pages
10.4236/jqis.2017.72006
Rare Top Decay t ® cg in General THDM-III
R. Gaitán-Lozano1*, J. H. Montes de Oca1, R. Martinez2
1Departamento de Física, FES-Cuautitlan, UNAM, Estado de México, México
2Departamento de Física, Universidad Nacional de Colombia, Bogotá D.C., Colombia
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 17, 2016; Accepted: May 21, 2017; Published: May 24, 2017
ABSTRACT
We study the decay 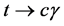 with flavor-changing neutral interactions in scalar sector of the type III Two Higgs Doublet Model (THDM-III) with mixing between neutral scalar fields as a result of considering the most general scalar potential. The branching ratio of the decay
with flavor-changing neutral interactions in scalar sector of the type III Two Higgs Doublet Model (THDM-III) with mixing between neutral scalar fields as a result of considering the most general scalar potential. The branching ratio of the decay 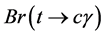 is calculated as function of the mixing parameters and masses of the neutral scalar fields. We obtain a
is calculated as function of the mixing parameters and masses of the neutral scalar fields. We obtain a 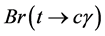 of the order of 10−8 for the considered regions of the mixing parameters. Finally, one upper bound for the possible events is estimated to be
of the order of 10−8 for the considered regions of the mixing parameters. Finally, one upper bound for the possible events is estimated to be  by assuming an expected luminosity of the order of 300 fb−1.
by assuming an expected luminosity of the order of 300 fb−1.
Keywords:
Two Higgs Doublet Models, Rare Top Decays

1. Introduction
A sensitive test for new physics is the processes of the top quark due to large mass. The predictions of the Standard Model (SM) for the top quark in flavor changing neutral (FCN) transitions are strongly suppressed [1] as a result of the Glashow-Iliopoulos-Maiani (GIM) mechanism [2] . However, rare decays with branching ratios (BR) of order 10−5 - 10−6 may be detectable, depending on the signal. Any hint for new top quark physics at LHC would motivate further study at the next generation of collider experiments [3] . Recent discovery of a SM-like Higgs boson with a mass near 125 - 126 GeV [4] [5] has generated new moti- vations to study the extended Higgs sector. The two-Higgs doublet model (2THDM) is one of the simplest extensions of the SM, adding a second Higgs doublet with the same quantum numbers as the first one [6] . The versions that involve natural flavor conservation and CP conservation in the potential through the introduction of a discrete symmetry, are known as 2HDM-I [7] [8] and 2HDM-II [9] . A general version which is named as 2HDM-III allows the presence of flavor-changing neutral scalar interactions (FCNSI) at a three-level [10] [11] . There are also some variants (known as top, lepton, neutrino), where one Higgs doublet couples predominantly to one type of fermion [12] , while in other models, it is even possible to identify a candidate for dark matter [13] [14] . The definition of all these models, depends on the Yukawa structure and symmetries of the Higgs sector, whose origin is still not known. The possible appearance of new sources of CP violation is another characteristic of these models [15] .
Within 2HDM-I where only one Higgs doublet generates all gauge and fermion masses, while the second doublet only knows about this through mixing, and thus the Higgs phenomenology will share some similarities with the SM, although the SM Higgs couplings will now be shared among the neutral scalar spectrum. The presence of a charged Higgs boson is clearly the signal beyond the SM. Within 2HDM-II, one also has natural flavor conservation [16] , and its phenomenology will be similar to the 2HDM-I, although in this case, the SM couplings are shared not only because of mixing, but also because of the Yukawa structure. The distinctive characteristic of 2HDM-III is the presence of FCNSI, which requires a certain mechanism in order to suppress them, for instance, one can impose a certain texture for the Yukawa couplings [17] , which will then predict a pattern of FCNSI Higgs couplings. Within all those models (2HDM-I, II, III) [18] , the Higgs doublets couple with all fermion families, with a strength proportional to the fermion masses, modulo other parameters.
In the present work, we calculate the the BR for the decay 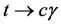 in the framework of the general 2HDM.
in the framework of the general 2HDM.
2. The General Two-Higgs-Dublet Model Type III
Given 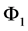 and
and 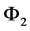 two complex
two complex 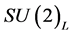 doublet scalar fields with hypercharge-one, the most general gauge invariant and renormalizable Higgs scalar potential is [19]
doublet scalar fields with hypercharge-one, the most general gauge invariant and renormalizable Higgs scalar potential is [19]
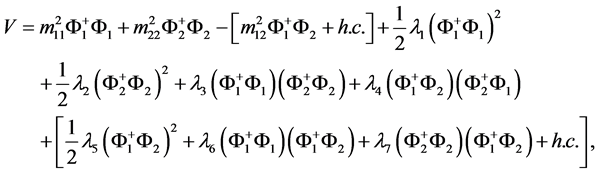 (1)
(1)
where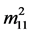 ,
, 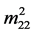 and
and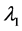 ,
, 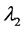 ,
, 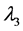 ,
, 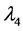 are real parameters and
are real parameters and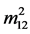 ,
, 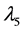 ,
, 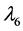 , and
, and 
Now, the most general 
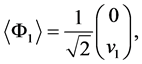

where we choose a basis in which 
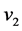

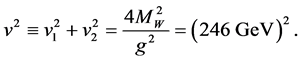
In the literature, the sign of the vev is chosen positive for convenience, however it could also take negative sign. The mass of the gauge fields are proportional to the square of the vev. The fermions have proportional masses to the vev then to be defined positively would take Yukawa couplings negative. In this way we would obtain consistent models and equal prediction regardless of the sign of the vev.
In Equation (2), the phase of 
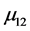
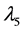

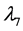
in the interaction basis can be written as
denote the real part. The third neutral scalar field in the interaction basis defined as 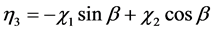




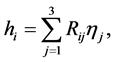
where R can be written down as:

and
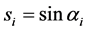

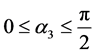
Higgs bosons 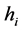

For the THDM with no CP violation in scalar sector the 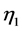
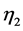
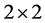


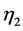
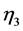

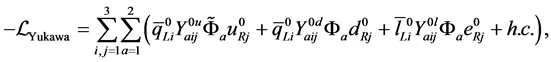
where 

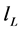

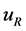



where 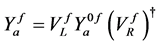
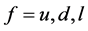
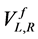
In order to study the rare top decay we are interested in up-type quarks fields. By using Equations (5), the interactions between neutral Higgs bosons and fermions can be written in the form of the 2HDM type II with additional contributions which arise from Yukawa couplings 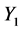
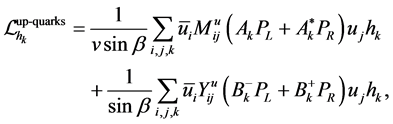
where
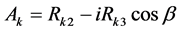
and
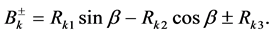
The fermion spinors are denoted as
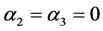
3. Rare Top Decay t ® cg
We are interested in the contributions of the flavor changing neutral scalar interactions to the rare top decay 

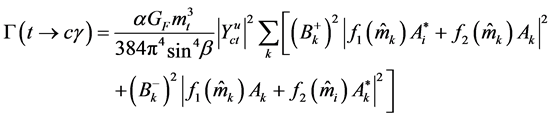
where



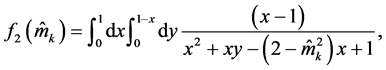
with
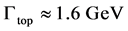
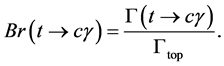
The above expression contains too many free parameters of the model, such as the masses Last expression contains several free parameters of the THDM, such as the masses of neutral Higgs bosons and the mixing parameter 
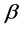
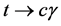
4. Mixing Parameters and Numerical Results
First we will discuss the free parameters involved in the process. The Yukawa couplings in the THDM-III are responsible for the FCNSI as shown the expression (9). One possible option to suppress these FCNSI is obtained by assuming an ansantz for the Yukawa couplings. We take into account the ansantz proposed by Cheng-Sher [23] . This ansatz assumes a specific structure for the Yukawa matrix given by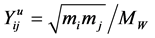
THDM type III in Yukawa Lagrangian has two sectors: in one of them the couplings are proportional to the masses of the fermions and does not generate flavor changing. The other sector generates flavor changing at tree level. This situation occurs because the two Yukawa matrices can not be diagonalized simultaneously with one rotation. The mass of the fermions and the factor that generates flavor changing are a linear combination of the two Yukawa matrices of the Lagrangian. Depending on this linear combination to generate the fermion masses, THDM type I or THDM type II can be generated plus additional terms that produce the flavor changes. In general THDM type III produces four different types of Lagrangians making linear combinations of type I and II for the up and down quarks. Then, in THDM type III we can choose the sector without flavor changing as type II and add the respective flavor changing that appear in this model. For this reason, a sector of parameters THDM type II in the various processes analyzed in the literature as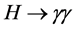


For the masses of neutral scalar 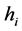




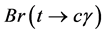
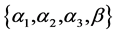
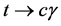


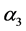
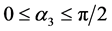





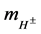

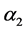


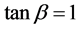
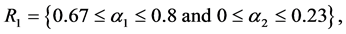
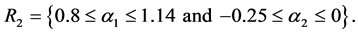
and
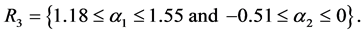
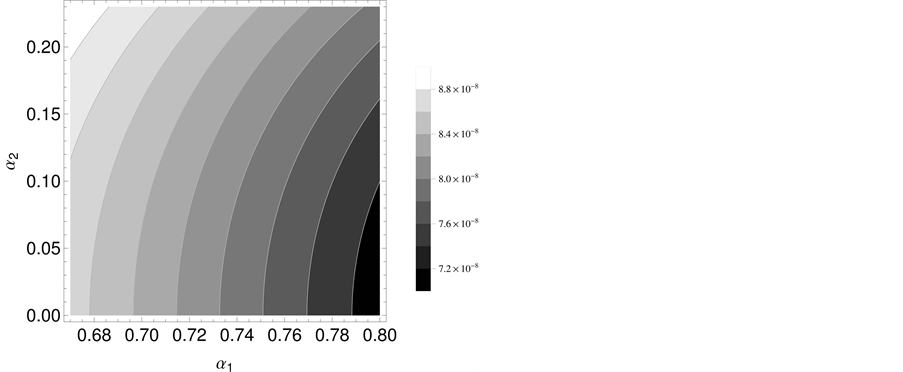
Figures 1-3 show the behavior of the branching ratio for 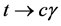

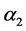


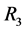
The obtained 


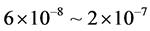
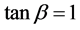
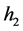

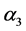

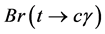
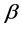
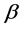
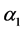
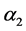

5. Conclusions
From 2015 to 2017, the experiment is expected to reach 100 fb−1 of data with a energy of the center of mass of 14 TeV. In the year 2021, it is expected to reach a luminosity of the order of 300 fb−1 of data. Experiments with this luminosity could find evidence of new physics beyond SM. Then, Run 3 in LHC could
Figure 1. Type III THDM branching ratio for 
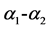
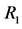
Figure 2. Type III THDM branching ratio for 


Figure 3. Type III THDM branching ratio for 

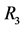
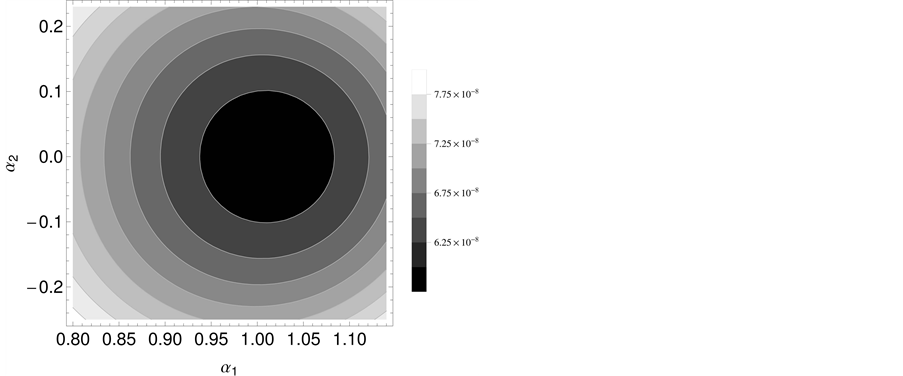
Figure 4. Scatter plot for branching ratio of the rare top decay as function of 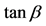
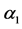
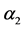
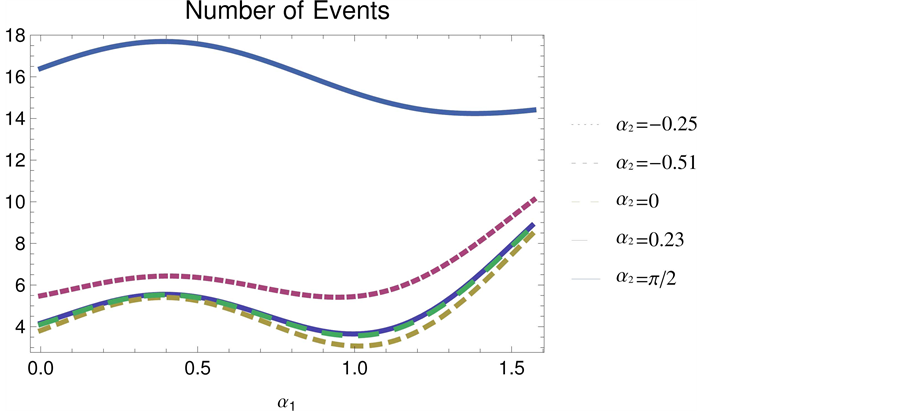
Figure 5. Events for 
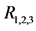
observe events for the flavor changing neutral processes, which can be explained in a naive form as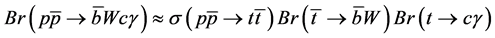
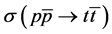
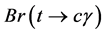
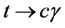
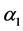
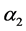

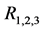
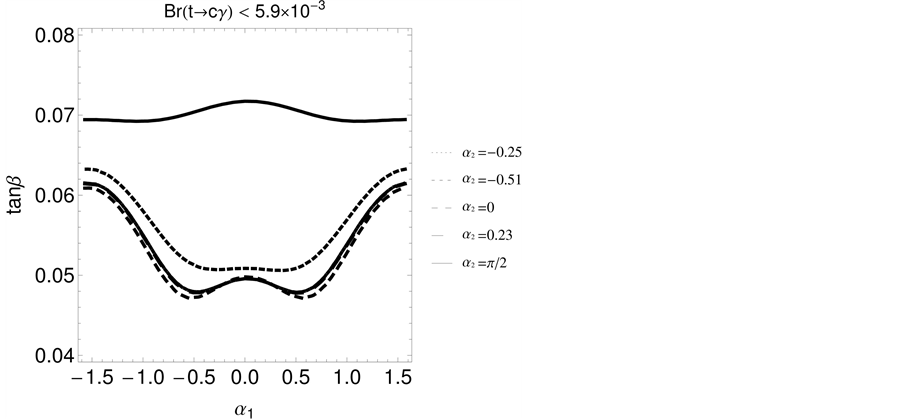
Last experimental results have obtained a bound for these branching ratios such as 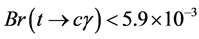
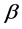

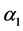
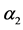
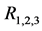
Figure 6. Solution to the equation 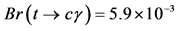
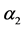
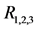
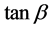

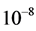
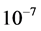
Acknowledgements
This work is supported in part by PAPIIT Project IN113916, Sistema Nacional de Investigadores (SNI) in México, and PIAPI 1628 Project. R. M. thanks to COLCIENCIAS for the financial support.
Cite this paper
Gaitán-Lozano, R., de Oca, J.H.M. and Martinez, R. (2017) Rare Top Decay t ® cg in General THDM- III. Journal of Quantum Information Science, 7, 57-66. https://doi.org/10.4236/jqis.2017.72006
References
- 1. Eilam, G., Hewett, J.L. and Soni, A. (1991) Rare Decays of the Top Quark in the Standard and Two-Higgs-Doublet Models. Physical Review D, 44, 1473.
https://doi.org/10.1103/PhysRevD.44.1473 - 2. Glashow, S.L., Iliopoulos, J. and Maiani, L. (1970) Weak Interactions with Lepton-Hadron Symmetry. Physical Review D, 2, 875.
https://doi.org/10.1103/PhysRevD.2.1285 - 3. Beneke, M., et al. (2000) Top quark physics. arXiv:hep-ph/0407319
- 4. ATLAS Collaboration (2012) Observation of a New Particle in the Search for the Standard Model Higgs. Boson with the ATLAS Detector at the LHC. Physics Letters B, 716, 1.
- 5. CMS Collaboration (2012) Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Physics Letters B, 716, 30.
- 6. Diaz, R. (2002) Phenomenological Analysis of the Two Higgs Doublet Model. Ph.D. Thesis. arXiv:hep-ph/0212237v2.
- 7. Haber, H.E., Kane, G.L. and Sterling, T. (1979) The Fermion Mass Scale and Possible Effects of Higgs Bosons on Experimental Observables. Nuclear Physics B, 161, 493.
- 8. Hall, L.J. and Wise, M.B. (1981) Flavor Changing Higgs-Boson Couplings. Nuclear Physics B, 187, 397.
- 9. Donoghue, J.F. and Li, L.F. (1979) Properties of Charged Higgs Bosons. Physical Review D, 19, 945.
https://doi.org/10.1103/PhysRevD.19.945 - 10. Cheng, T.P. and Sher, M. (1987) Mass-Matrix Ansatz and Flavor Nonconservation in Models with Multiple Higgs Doublets. Physical Review D, 35, 3484.
https://doi.org/10.1103/PhysRevD.35.3484 - 11. Crivellin, A., Kokulu, A. and Greub, C. (2013) Flavor-Phenomenology of Two-Higgs-Doublet Models with Generic Yukawa Structure. Physical Review D, 87, Article ID: 094031. hep-ph/1303.5877
- 12. Branco, G.C., Ferreira, P.M., Lavoura, L., Rebelo, M.N., Sher, M. and Silva, J.P. (2012) Theory and Phenomenology of Two-Higgs-Doublet Models. Physics Reports, 516, 1. hep-ph/1106.0034
- 13. Dolle, E.M. and Su, S. (2009) Inert Dark Matter. Physical Review D, 80, Article ID: 055012. hep-ph/0906.1609
https://doi.org/10.1103/PhysRevD.80.055012 - 14. Cirelli, M., Fornengo, N. and Strumia, A. (2006) Minimal Dark Matter. Nuclear Physics B, 753, 178. hep-ph/0512090
- 15. Ginzburg, I.F. and Krawczyk, M. (2005) Symmetries of Two Higgs Doublet Model and CP Violation. Physical Review D, 72, Article ID: 115013. hep-ph/0408011
- 16. Glashow, S.L. and Weinberg, S. (1977) Natural Conservation Laws for Neutral Currents. Physical Review D, 15, 1958.
https://doi.org/10.1103/PhysRevD.15.1958 - 17. Fritzsch, H. (1977) Calculating the Cabibbo Angle. Physics Letters B, 70, 436.
- 18. Carcamo Hernandez, A.E., Martinez, R. and Rodriguez, J.A. (2007) Different Kind of Textures of Yukawa Coupling Matrices in the Two Higgs Doublet Model Type III. The European Physical Journal C, 50, 935. hep-ph/0606190
- 19. Haber, H.E. and Hempfling, R. (1993) Renormalization-Group-Improved Higgs Sector of the Minimal Supersymmetric Model. Physical Review D, 48, 4280.
https://doi.org/10.1103/PhysRevD.48.4280 - 20. Arhrib, A., Christova, E., Eberl, H. and Ginina, E. (2011) CP Violation in Charged Higgs Production and Decays in the Complex Two Higgs Doublet Model. JHEP, 1104, Article ID: 089. hep-ph/1011.6560.
- 21. Diaz-Cruz, J.L., Martinez, R., Perez, M.A. and Rosado, A. (1990) Flavor-Changing Radiative Decay of the t Quark. Physical Review D, 41, 891.
https://doi.org/10.1103/PhysRevD.41.891 - 22. Beringer, J., et al. (2012) Review of Particle Physics. Physical Review D, 86, Article ID: 010001.
https://doi.org/10.1103/PhysRevD.86.010001 - 23. Cheng, T.P. and Sher, M. (1987) Mass-Matrix Ansatz and Flavor Nonconservation in Models with Multiple Higgs Doublets. Physical Review D, 35, 3484.
tps://doi.org/10.1103/PhysRevD.35.3484 - 24. Gaitan-Lozano, R., Martinez, R., Montes de Oca, J.H., et al. (2014) Rare Top Decay and CP Violation in THDM. The European Physical Journal, 74, 2788.
https://doi.org/10.1140/epjc/s10052-014-2788-4 - 25. Basso, L., Lipniacka, A., Mahmoudi, F., Moretti, S., Osland, P., Pruna, G.M. and Purmohammadi, M. (2012) Probing the Charged Higgs Boson at the LHC in the CP-Violating Type-II 2HDM. JHEP, 1211, 011. hep-ph/1205.6569
- 26. Mele, B., Petrarca, S. and Soddu, A. (1998) A New Evaluation of the t→cH Decay Width in the Standard Model. Physics Letters B, 435, 401.
hep-ph/9805498