Received 10 November 2015; accepted 25 December 2015; published 30 December 2015

ABSTRACT

As the fundamental theory of quantum information science, recently I proposed the linguistic interpretation of quantum mechanics, which was characterized as the linguistic turn of the Copenhagen interpretation of quantum mechanics. This turn from physics to language does not only extend quantum theory to classical theory but also yield the quantum mechanical world view. Although the wave function collapse (or more generally, the post-measurement state) is prohibited in the linguistic interpretation, in this paper I show that the phenomenon like wave function collapse can be realized. That is, the projection postulate is completely clarified in the linguistic interpretation.

Keywords:

Linguistic Interpretation, Copenhagen Interpretation, Wave Function Collapse, von Neumann-Lüders Projection Postulate

1. The Linguistic Interpretation of Quantum Mechanics

Recently in [1] -[4] , I proposed quantum language (i.e., the linguistic interpretation of quantum mechanics, or measurement theory), which was characterized as the linguistic turn of the Copenhagen interpretation of quantum mechanics. This turn from physics to language does not only extend quantum theory to classical theory but also yield the quantum mechanical world view. Also, I believe that the linguistic interpretation is the true colors of the Copenhagen interpretation, though there are a lot of opinions about the Copenhagen interpretation (cf. [5] ).

As mentioned in a later section (Section 1.3 (C)), the wave function collapse (or more generally, the post- measurement state) is prohibited in the linguistic interpretation. Thus, some asked me “How is the projection postulate?”. This question urges me to write this paper. The reader who would like to know only my answer may skip this section and read from Section 2.

1.1. Preparations

Now we briefly introduce quantum language as follows.

Consider an operator algebra 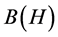(i.e., an operator algebra composed of all bounded linear operators on a

Hilbert space H with the norm), and consider the pair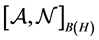, which is called a basic structure. Here, 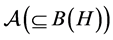is a 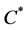-algebra, and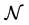 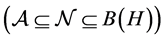is a particular 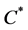-algebra

(called a 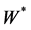-algebra) such that is the weak closure of 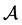in.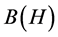

The measurement theory (=quantum language = the linguistic interpretation) is classified as follows.

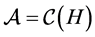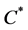That is, when, the -algebra composed of all compact operators on a Hilbert space H, the (A₁) is called quantum measurement theory (or, quantum system theory), which can be regarded as the linguistic aspect of quantum mechanics. Also, when is commutative (that is, when is characterized by, the -algebra composed of all continuous complex-valued functions vanishing at infinity on a locally compact Hausdorff space ( cf. [6] [7] )), the (A₂) is called classical measurement theory.

Also, note that, when,

1) (=trace class), , (i.e., pre-dual space), thus, ().

Also, when,

2) = “the space of all signed measures on”, , , where is some measures on, thus, () (cf. [6] ).

Let be a -algebra, and let be the dual Banach space of. That is, , and the norm is defined by . Define the mixed state such that and for all such that. And define the mixed state space such that

A mixed state is called a pure state if it satisfies that “for some and” implies “”. Put

which is called a state space. It is well known (cf. [6] ) that , and, where . The latter implies that can be also identified with (called a spectrum space or simply spectrum) such as

(1)

For instance, in the above 2) we must clarify the meaning of the “value” of for and

. An element is said to be essentially continuous at, if there uniquely exists a complex number such that

(B) If converges to in the sense of weak^* topology of, that is,

(2)

then converges to.

And the value of is defined by the.

According to the noted idea (cf. [8] ), an observable in is defined as follows:

1) [-field] X is a set, (, the power set of X) is a -field of X, that is, “”, “”.

2) [Countable additivity] F is a mapping from to satisfying: a): for every, is a non-negative element in such that, b): and, where 0 and I is the

0-element and the identity in respectively, c): for any countable decomposition of (i.e., , ,), it holds that in the sense of weak^* topology in.

1.2. Axiom 1 [Measurement] and Axiom 2 [Causality]

Measurement theory (A) is composed of two axioms (i.e., Axioms 1 and 2) as follows. With any system S, a basic structure can be associated in which the measurement theory (A) of that system can be formulated. A state of the system S is represented by an element and an observable is represented by an observable in. Also, the measurement of the observable for the system S with the

state is denoted by (or more precisely,). An observer can obtain a measured value x () by the measurement.

The Axiom 1 presented below is a kind of mathematical generalization of Born’s probabilistic interpretation of quantum mechanics. And thus, it is a statement without reality.

Now we can present Axiom 1 in the -algebraic formulation as follows.

Axiom 1 [Measurement]. The probability that a measured value x () obtained by the measurement belongs to a set is given by if is essentially continuous at.

Next, we explain Axiom 2. Let and be basic structures. A continuous linear operator (with weak^* topology) (with weak^* topology) is called a Markov operator, if it satisfies that 1): for any non-negative element in, 2):, where is the identity in,. In addition to the above 1) and 2), we assume that and .

It is clear that the dual operator satisfies that. If it holds that, the is said to be deterministic. If it is not deterministic, it is said to be non-

deterministic. Also note that, for any observable in, the is an observable in.

Now Axiom 2 is presented as follows (For details, see [4] ).

Axiom 2 [Causality]. Let. The causality is represented by a Markov operator.

1.3. The Linguistic Interpretation

In the above, Axioms 1 and 2 are kinds of spells, (i.e., incantation, magic words, metaphysical statements), and thus, it is nonsense to verify them experimentally. Therefore, what we should do is not “to understand” but “to use”. After learning Axioms 1 and 2 by rote, we have to improve how to use them through trial and error.

We can do well even if we do not know the linguistic interpretation (=the manual to use Axioms 1 and 2). However, it is better to know the linguistic interpretation, if we would like to make progress quantum language early.

The essence of the manual is as follows:

(C) Only one measurement is permitted. And thus, the state after a measurement is meaningless since it cannot be measured any longer. Hence, the wave function collapse is prohibited. We are not concerned with the problem: “When is a measurement taken?”. Also, the causality should be assumed only in the side of system, however, a state never moves. Thus, the Heisenberg picture should be adopted, and thus, the Schrödinger picture should be prohibited.

and so on. For details, see [4] .

2. The Wave Function Collapse (i.e., the Projection Postulate)

From here, I devote myself to quantum system (A₁) (and not classical system (A₂)).

2.1. Problem: The von Neumann-Lüders Projection Postulate

Let be a quantum basic structure. Let be a countable set. Consider the projection valued observable in. Put

(3)

Axiom 1 says:

(D₁) The probability that a measured value is obtained by the measurement is given by

(4)

Also, the von Neumann-Lüders projection postulate (in the Copenhagen interpretation, cf. [9] [10] ) says:

(D₂) When a measured value is obtained by the measurement, the post-measurement state is given by

And therefore, when a next measurement is taken (where is arbitrary observable in), the probability that a measured value belongs to is given by

(5)

Problem 1. In the linguistic interpretation, the phrase: post-measurement state in the (D₂) is meaningless. Also, the above (=(D₁) + (D₂)) is equivalent to the simultaneous measurement, which does

not exist in the case that and do not commute. Hence the (D₂) is meaningless in general. Therefore, we have the following problem:

(E) Instead of the in, what observable should be chosen?

In the following section, I answer this problem within the framework of the linguistic interpretation.

2.2. The Derivation of von Neumann-Lüders Projection Postulate in the Linguistic Interpretation

Consider two basic structure and. Let be as in Section 2.1, and let be a complete orthonormal system in a Hilbert space K. Define the predual Markov operator by, for any,

(6)

or

(7)

Thus the Markov operator ( in Axiom 2) is defined by.

Define the observable in such that

Let be arbitrary observable in. Thus, we have the tensor observable in, where is the product -field.

Fix a pure state . Consider the measurement. Then, we see that

(F) the probability that a measured value obtained by the measurement belongs to is given by

(In a similar way, the same result is easily obtained in the case of (7)).

Thus, we see the following.

(G₁) if, then

(8)

(G₂) in case that a measured value belongs to, the conditional probability such that is given by

(9)

where it should be recalled that is arbitrary. Also note that the above (i.e., the projection postulate (G)) is a consequence of Axioms 1 and 2.

Considering the correspondence: (D) Û (G), that is,

namely,

there is a reason to assume that the true meaning of the (D) is just the (G). Also, note the taboo phrase “post- measurement state” is not used in (G₂) but in (D₂). Hence, we obtain the answer of Problem 1 (i.e.,).

Remark 1. So called Copenhagen interpretation may admit the post-measurement state (cf. [5] ). Thus, in this case, some may think that the post-measurement state is obtained by the formula (9). However,

this idea would not generally be approved. That is because, if the post-measurement state is admitted, a series of problems occur, that is, “When is a measurement taken?”, or “When does the wave function collapse happen?”, which is beyond Axioms 1 and 2. Readers should remember Wittgenstein’s famous word: “The limits of my language mean the limits of my world”, or “What we cannot speak about we must pass over in silence”.

3. Conclusions

As mentioned in Section 1.3 (C), the wave function collapse (or more generally, the post-measurement state) is prohibited in the linguistic interpretation. Hence, some asked me “How about the projection postulate?”. In this paper I answer this question as follows:

(H) The von Neumann-Lüders projection postulate (D₂) concerning the measurement does not hold (i.e., (D₂) is wrong). However, in the linguistic interpretation (i.e., without the phrase: “post-measure- ment state”), the similar result (G₂) concerning holds.

As mentioned in Remark 1, the projection postulate (i.e., wave function collapse) is not completely established in so called Copenhagen interpretation, and thus, it is usually regarded as “postulate”. However, in the linguistic interpretation, the projection postulate is completely clarified, and hence, it should be regarded as a theorem. I hope that confusion on the wave function collapse will be calming.

Cite this paper

ShiroIshikawa, (2015) Linguistic Interpretation of Quantum Mechanics; Projection Postulate. Journal of Quantum Information Science,05,150-155. doi: 10.4236/jqis.2015.54017

References