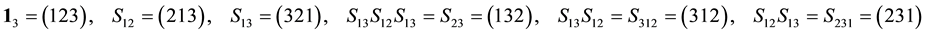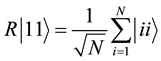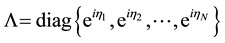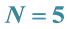Journal of Quantum Information Science
Vol.05 No.01(2015), Article ID:55019,7 pages
10.4236/jqis.2015.51003
Constructing Entanglers in 2-Players?N-Strategies Quantum Game
Yshai Avishai
Department of Physics and the Ilse Katz Center for Nano-Science, Ben-Gurion University, Beersheba, Israel
Email: yshai@bgu.ac.il
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 October 2014; accepted 24 March 2015; published 25 March 2015
ABSTRACT
In quantum games based on 2-player-N-strategies classical games, each player has a quNit (a normalized vector in an N-dimensional Hilbert space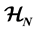 ) upon which he applies his strategy (a matrix
) upon which he applies his strategy (a matrix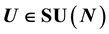 ). The players draw their payoffs from a state
). The players draw their payoffs from a state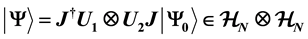 . Here
. Here 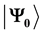 and
and 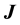 (both determined by the game’s referee) are respectively an unentangled 2- quNit (pure) state and a unitary operator such that
(both determined by the game’s referee) are respectively an unentangled 2- quNit (pure) state and a unitary operator such that  is partially entangled. The existence of pure strategy Nash equilibrium in the quantum game is intimately related to the degree of entanglement of
is partially entangled. The existence of pure strategy Nash equilibrium in the quantum game is intimately related to the degree of entanglement of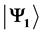 . Hence, it is practical to design the entangler
. Hence, it is practical to design the entangler  to be dependent on a single real parameter
to be dependent on a single real parameter 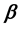 that controls the degree of entanglement of
that controls the degree of entanglement of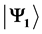 , such that its von-Neumann entropy
, such that its von-Neumann entropy 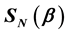 is continuous and obtains any value in
is continuous and obtains any value in . Designing
. Designing  for
for 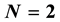 is quite standard. Extension to
is quite standard. Extension to 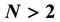 is not obvious, and here we suggest an algorithm to achieve it. Such construction provides a special quantum gate that should be a useful tool not only in quantum games but, more generally, as a special gate in manipulating quantum information protocols.
is not obvious, and here we suggest an algorithm to achieve it. Such construction provides a special quantum gate that should be a useful tool not only in quantum games but, more generally, as a special gate in manipulating quantum information protocols.
Keywords:
Quantum Games, Qubits, Qutrits, quNits, Controlled Entanglement, von Neumann Entropy

1. Introduction
The theory of quantum games is an evolving discipline that, similar to quantum information [1] [2] , explores the implications of quantum mechanics to fields outside physics proper, such as economics, finance, auctions, gambling, etc. [3] - [9] . One way of constructing a quantum game is to start from a standard (classical) game and to “quantize” it by formulating appropriate rules and letting the players employ quantum information tools such as qubits and quantum gates (or strategies in the quantum game nomenclature). This procedure has been applied on classical strategic games that describe an interactive decision-making in which each player chooses his strategy only once, and all choices are taken simultaneously. A simple example is a quantum game based on 2-player-2- strategies classical game usually defined by a game table (for example, the prisoner dilemma). We refer to it briefly as a 2-2 game.
2. Quantum Games: The Role of Entanglement
There is an extensive work on the quantized version of classical strategic 2-2 games, most of them are based on the protocol specified in [5] . It requires application of an entanglement (unitary) operator 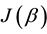 (where β is a real parameter), which acts on a non-entangled 2-qubit (pure) state resulting in an entangled state whose degree of entanglement is measured by its von-Neumann entropy
(where β is a real parameter), which acts on a non-entangled 2-qubit (pure) state resulting in an entangled state whose degree of entanglement is measured by its von-Neumann entropy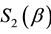
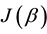
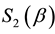
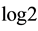
Controlling the entropy by a single parameter that all values between 0 and 

3. Classical Commensurability
Another practical property required from 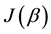

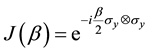

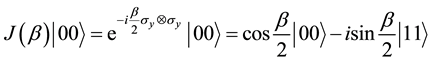
where the left (right) factor in the Kronecker product refers to player 1 (2). In this way, 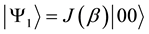
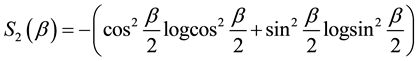
Thus, 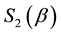
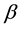
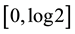
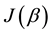
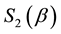
periodic with period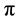
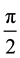
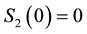
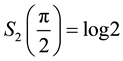
The entangler defined in Equation (1) has a property referred to as classical commensurability,
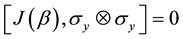

4. The Present Work
In the present work we examine the issue of constructing 

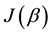
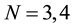
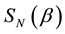
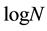
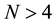
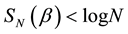
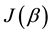
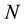
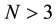

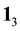
5. Two-Players-Three-Strategies Classical Games: Trits
Consider a two-players classical game with three strategies for each player. For example, two prisoners may have three options, marked as three values of a trit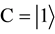
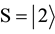
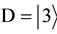

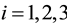
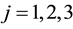



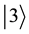

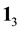
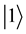

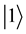


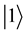
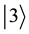
by D). These three operations generate the group 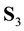
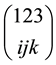
We shall indicate below that a quantum strategy is a gate represented by an 
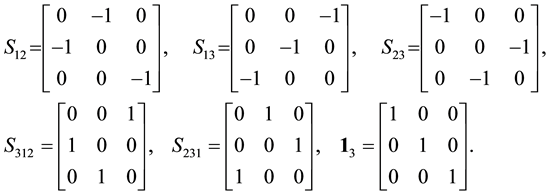
For example, suppose player 1 and 2 choose respective strategies 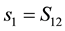
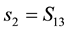
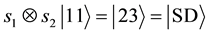
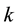
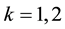
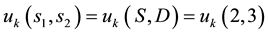
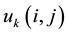
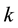
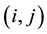
6. The Analogous Quantum Game: 1 and 2 Quirt States
We now briefly explain the structure of the corresponding quantum game. Its main ingredients are qutrits, quantum strategies, and entanglement operations. Both versions use the same game table but the payoff rules are somewhat different.
Consider the three dimensional Hilbert space 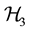
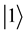

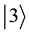
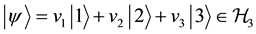

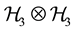
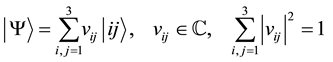
A maximally entangled two-qutrit state is written as
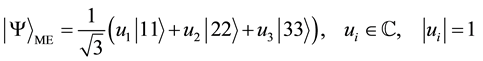
given in a Schmidt decomposed form. Its entanglement degree is measured by the von Neumann entropy
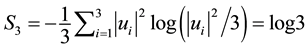
7. 2-3 Quantum Game Strategies
A strategy of a player in a 2-3 quantum game is an 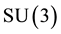
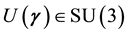
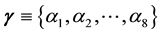
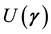
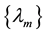
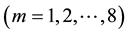
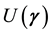
8. 2-3 Quantum Game Procedure
The referee suggests an initial non-entangled two-qutrit state 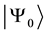


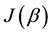
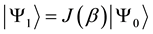
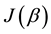
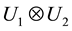
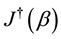
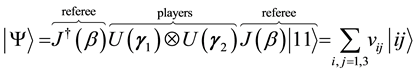
where 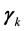

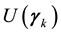
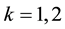

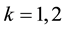
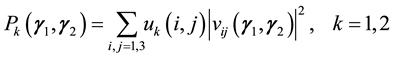
where 
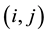
9. Pure Strategy Nash Equilibrium (NE)
Because the set of 8 Euler angles 
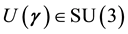
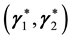
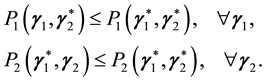
The question of whether pure strategy NE exists in a 2-2 quantum game and its relation to the degree of entanglement (controlled by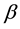
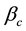

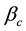
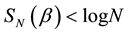
10. Absence of Classical Commensurability
We now explain why in a 2-3 quantum game there is no classical commensurability [10] . Recall that classical commensurability means that if the players use classical strategies they respectively get their classical payoffs. For a classical strategy 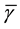
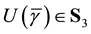


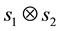
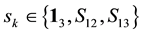
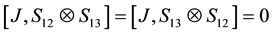
This is possible only if J is a function of 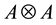

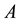
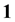
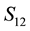
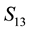
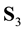

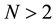
11. Designing the Entangler
The main result of the present study concerns the analysis and construction of an entanglement operator 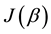
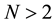
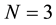
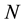
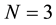

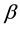
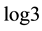
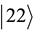
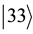
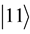

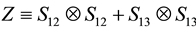
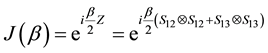
Calculation of the exponent yields
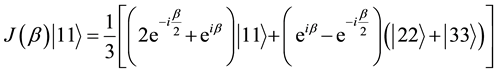
Maximal entanglement obtains when the absolute values of all three coefficients are equal, namely

Here 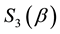
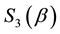
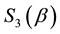
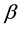

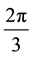
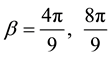
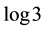
we see that, in quantum games, the entanglement is not obtained in terms of spin rotations but, rather, in terms of permutation exponentials that are SU(3) matrices (for 
12. Extension to Arbitrary N
Let 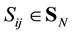


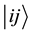
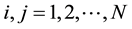
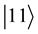
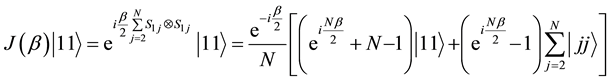
To proceed, let us define the absolute value squared of the coefficients
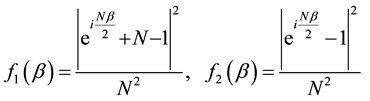
It is easy to verify that: 1)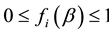

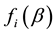
riod 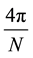
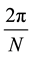

Maximal entanglement 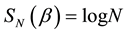
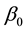
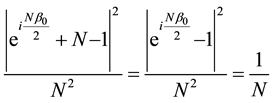
For 
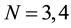
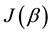
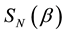
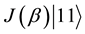
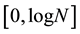
For 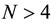

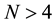
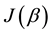
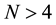
The method suggested here is not based on permutation exponentials as in Equation (10). It consists of the following steps.
1) Assume a lexicographic order of the 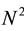
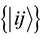
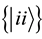
the first N places. Choose a unitary 
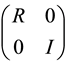
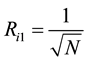
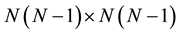
then reduced to the 
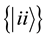
that is a maximally entangled state.
2) Diagonalize 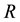
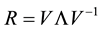
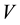
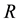
is the diagonal matrix of (unimodular) eigenvalues of 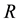
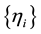
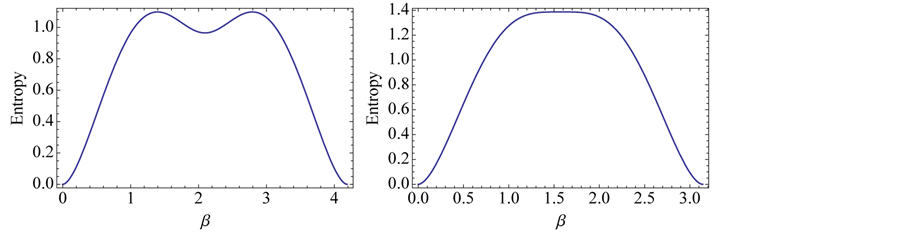
Figure 1. von Neumann entropy 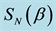
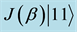
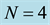


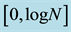
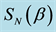
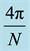
3) Now consider the matrix
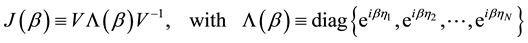
By construction, 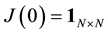
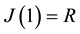
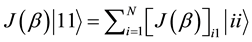
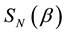

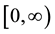
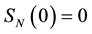

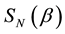
13. Illustration for
A convenient way to build an appropriate unitary 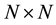
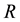
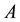
Proceeding with the list of steps prescribed above we can easily construct 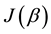
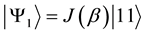
As explained in the figure’s caption, the degree of entanglement is controlled by a single parameter and 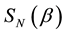
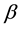
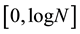
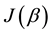
14. Summary
In conclusion, we suggest two methods to design an entanglement operator 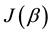
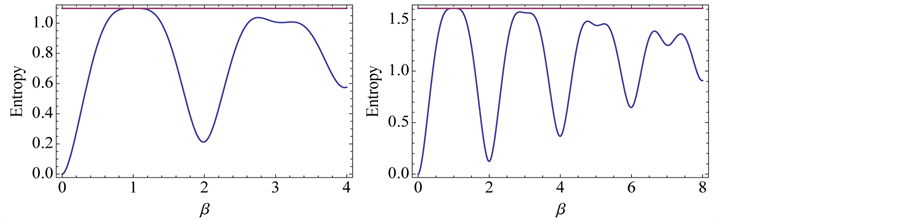
Figure 2. von Neumann entropy for 2-quNit state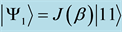
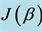
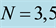
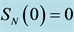

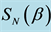
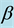
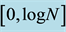

2-quNit state to a partially entangled state whose von Neumann entropy is fully controlled by a single real parameter. The first method is intuitively clear and simple, based on exponential of classical strategies, Equation (10), and results in the von Neumann entropy, as displayed in Figure 1. This method does not work for 
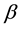
The entangler 
Acknowledgements
I would like to thank Oscar Vollij for his excellent course in (classical) game theory. Discussions with Eytan Bachmat, Hosho Katsura, Rioichi Shindou, Doron Cohen and Yehuda Band are highly appreciated. This work is partially supported by grant 400/2012 of the Israeli Science Foundation (ISF).
References
- Nielsen, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge, p 26, Fig. 1.13.
- Band, Y.B. and Avishai, Y. (2013) Quantum Mechanics with Application to Nanotechnology and Information Science. Academic Press, Waltham, p 217.
- Goldenberg, L., Vaidman, L. and Wiesner, S. (1999) Quantum Gambling. Physical Review Letters, 82, 3356. http://dx.doi.org/10.1103/PhysRevLett.82.3356
- Meyer, D. (1999) Quantum Strategies. Physical Review Letters, 82, 1052-1055. http://dx.doi.org/10.1103/PhysRevLett.82.1052
- Eisert, J., Wilkens, M. and Lewenstein, M. (1999) Quantum Games and Quantum Strategies. Physical Review Letters, 83, 3077-3080. http://dx.doi.org/10.1103/PhysRevLett.83.3077
- Flitney, A.P. and Abbott, D. (2002) An Introduction to Quantum Game Theory. Fluctuation and Noise Letters, 2, R175-R187. arXiv: quant-ph/0208069. http://dx.doi.org/10.1142/S0219477502000981
- Piotrowski, E.W. andSlaadkowski, J. (2003) An Invitation to Quantum Game Theory. International Journal of Theoretical Physics, 42, 1089-1099. http://dx.doi.org/10.1023/A:1025443111388
- Landsburg, S.E. (2004) Quantum Game Theory. Notices of the American Mathematical Society, 51, 394-399.
- Iqbal, A. (2004) Studies in the Theory of Quantum Games. Ph.D thesis, Quaid-i-Azam University, Islamabad, 137 p. arXiv:quant-phys/050317.
- Sharif, P. and Heydari, H. (2014) Quantum Information and Computation, 14, 0295.
- Landsburg, S.E. (2011) Nash Equilibria in Quantum Games. Proceedings of the American Mathematical Society, 139, 4423-4434. arXiv:1110.1351.
- Benjamin, S.C. and Hayden, P.M. (2001) Comment on “Quantum Games and Quantum Strategies”. Physical Review Letters, 87, Article ID: 069801. http://dx.doi.org/10.1103/PhysRevLett.87.069801
- Du, J., Li, H., Xu, X., Han, R. and Zhou, X. (2002) Entanglement Enhanced Multiplayer Quantum Games. Physics Letters A, 302, 229-233. http://dx.doi.org/10.1016/S0375-9601(02)01144-1
- Du, J., Xu, X., Li, H., Zhou, X. and Han, R. (2002) Playing Prisoner’s Dilemma with Quantum Rules. Fluctuation and Noise Letters, 2, R189. http://dx.doi.org/10.1142/S0219477502000993
- Flitney, A.P. and Abbott, D. (2003) Advantage of a Quantum Player over a Classical One in 2 × 2 Quantum Games. Proceedings of the Royal Society A, 459, 2463-2474. http://dx.doi.org/10.1098/rspa.2003.1136
- Flitney, A.P. and Hollenberg, L.C.L. (2007) Nash Equilibria in Quantum Games with Generalized Two-Parameter Strategies. Physics Letters A, 363, 381-388. http://dx.doi.org/10.1016/j.physleta.2006.11.044
- Avishai, Y. (2012) Some Topics in Quantum Games. MA Thesis in Economics, Ben Gurion University, Beersheba, 96 p. arXiv:1306.0284. (Submitted on August 2012 to the Faculty of Social Science and Humanities at the Ben Gurion University).
- Osborne, M.J. and Rubinstein, A. (2011) A Course in Game Theory. The MIT Press, Version: 2011-1-19. Cambridge, Massachusetts, London, England.