Journal of Quantum Information Science
Vol.04 No.04(2014), Article ID:52402,12 pages
10.4236/jqis.2014.44020
Time Dependent Entropy and Decoherence in a Modified Quantum Damped Harmonic Oscillator
F. B. Pelap1*, A. Fomethe1, A. J. Fotue2, M. P. Djemmo Tabue1,2
1Laboratoire de Mécanique et de Modélisation des Systèmes Physiques (L2MSP), Faculté des Sciences, Université de Dschang, Dschang, Cameroon
2Laboratory of Mesoscopy and Multilayers Structures, Faculty of Science, University of Dschang, Dschang, Cameroon
Email: *fbpelap@yahoo.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 November 2014; revised 2 December 2014; accepted 9 December 2014
ABSTRACT
The time dependence of probability and Shannon entropy of a modified damped harmonic oscillator is studied by using single and double Gaussian wave functions through the Feynman path method. We establish that the damped coefficient as well as the system frequency and the distance separating two consecutive waves of the initial double Gaussian function influences the coherence of the system and can be used to control its decoherence.
Keywords:
Modified Damped Harmonic Oscillator, Feynman Path Integral, Decoherence, Shannon Entropy, Distribution Probability

1. Introduction
The study of dissipative systems and their quantization is of a great theoretical and practical value in view of many different situations in which dissipative phenomena with a quantum origin manifest themselves [1] . Within these dissipative systems, the damped harmonic oscillator (DHO) is the simplest quantum systems displaying the dissipation of energy. It is of great physical importance and has found many applications especially in quantum optics [2] [3] . For example, it plays a central role in the quantum theory of lasers and masers [4] . Moreover, damped harmonic oscillators are used to investigate the quantum decoherence (QD) phenomenon whose role became relevant in many interesting physical problems such as quantum computation and quantum information processing [5] , material science [6] - [8] , heavy ion collisions [9] , quantum gravity and cosmology [10] - [22] , and condensed matter physics [23] - [25] . In many cases, physicists are interested in understanding the causes of QD in order to prevent decoherence from damaging quantum states and protect the information stored in these states. Thus, decoherence is responsible for washing out the quantum interference effects which are desirable to be seen as signals in some experiments. However, QD has negative effects in many areas such as quantum computation and quantum control of atomic and molecular processes. The physics of information and computation is a domain where decoherence is an obvious major obstacle in the implementation of information-processing hardware. It takes advantage on the superposition principle [26] . QD is a condition that has to be satisfied in order that a system could be considered as classical. This condition requires that the system should be in one of relatively permanent states (called by Zurek “preferred states”) and the interference between different states should be negligible [27] [28] . The loss of coherence can be achieved by introducing an interaction between the system and environment [23] [29] [30] .
Nowadays, a great deal of research is dedicated to understanding decoherence in harmonic oscillator [31] [32] . Isar et al. [33] determine the degree of quantum decoherence of a harmonic oscillator interacting with a thermal bath using Lindblad theory [34] [35] . Other authors [36] use a semi-classical approach to examine decoherence in a harmonic oscillator coupled to a thermal harmonic bath. Darius et al. [37] exploit the Feynman path integral to study the memory in a non-locally damped oscillator. Moreover, Ozgur et al. [32] determine the time dependence of Leipnik’s entropy in the damped harmonic oscillator via path integral techniques. Another strategy to describe dissipative quantum systems is based on the idea of Bateman [38] .
In this paper, we investigate the coherence of the damped harmonic oscillator using the Caldirola-Kanai model [39] but based on the idea of Bateman [38] . This model is known as a popular model used to describe dissipative systems coupled to a harmonic bath. It has many applications like reproducing classical effects or giving a good Hamiltonian necessary to exhibit the phenomenon of decoherence [38] . This paper is organized as follows. In Section 2, we present the mathematical tools based on the path integral formalism. We also discuss the case of the damped harmonic oscillator and build the associated propagator. In Section 3, we derive the general expressions of the thermodynamic parameters of the system, and analyze the effects of the damping constant on the distribution probability and the Shannon entropy for a single Gaussian wave function. The influence of the system’s frequency has also been measured on these parameters. Hence, we consider a double Gaussian wave function and make numerical investigations appreciate the impact of the damping constant, the distance separating the two wave functions and the system’s frequency on the thermodynamic characteristics of the system. Discussion and concluding remarks are given in the last section.
2. Fundamental Definitions
We start by presenting the model which consists of a particle of mass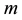 , labeled by the position variable
, labeled by the position variable 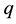 and the momentum
and the momentum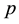 . Then follows the description of the used mathematical tools which is the path integral formalism introduced by Feynman [40] . These tools suggest that the transformation function called propagator is
. Then follows the description of the used mathematical tools which is the path integral formalism introduced by Feynman [40] . These tools suggest that the transformation function called propagator is
analogue to 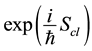 in which
in which 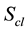 stands for the action, solution of Hamilton-Jacobi equation. On the other
stands for the action, solution of Hamilton-Jacobi equation. On the other
way, the transition amplitude of the particle (of mass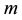 ) from the position
) from the position 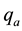 at time
at time 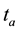 to the position
to the position  at time
at time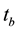 , known as the propagator, represents the solution of the Schrodinger equation. Nowadays, several problems of physics are solved via these techniques [32] [41] .
, known as the propagator, represents the solution of the Schrodinger equation. Nowadays, several problems of physics are solved via these techniques [32] [41] .
Next, we consider the Bateman Hamiltonian [38] defined as:
 (1)
(1)
where  and
and 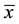 are the mirror variables corresponding to the coordinate
are the mirror variables corresponding to the coordinate  and the momentum
and the momentum . The quantities
. The quantities 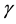 and
and 
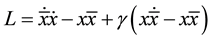
Using Euler-Lagrange equation, we derive the following two motion equations [42] :
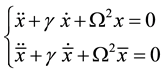
Bateman’s dual Hamiltonian describes classical mechanics correctly, but this model faces some difficulties. It violates Heisenberg’s principle for


Here, 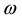

The classical solution of (5) is given by
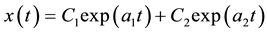
where in 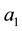





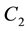
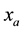

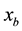


whose computation for the current study case leads to:

in which we set:
From the classical action, the expression of the corresponding propagator is defined below.

Substituting (7) into (8), we obtain the following expression for the quantum propagator of damped harmonic oscillator:

This result is identical to the one establish in [41] using the propagator method developed by Um et al. [43] . It also appears from (9) that the propagator 

Hereafter, we intend to use the propagator (9) and derive some characteristic parameters (such as the distribution probability and the Shannon entropy) of the system subjected respectively to single and double Gaussian wave functions. These investigations aim to measure the impact of the environment on the behavior of the system when the latter progresses.
3. Calculations and Results
3.1. System Properties under a Single Gaussian Wave Function
In this section, we exploit the single Gaussian wave function to examine the impact of the environment on the distribution probability and the Shannon entropy for a specific damped harmonic oscillator and therefore, to measure its coherence.
3.1.1. Distribution Probability
Making use of [31] , we determine the distribution probability for a single Gaussian wave packet to find the particle at coordinate 


which presents the link between the distribution probability 


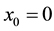

The quantity 
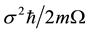
which takes the following form after substitution of the classical action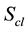

With

Therefore, the distribution probability (10) yields the following expression:

This relation shows that the distribution probability is an explicit function of space and time. Figure 1(a) presents its evolution when the damping coefficient 



Figure 1. Distribution probability for a single Gaussian wave function with the parameters
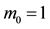




From the obtained curve, one observes that the probability increases with the growth of the damping coefficient. This result traduces the fact that the interaction between the system and the environment induces a modification of the former. It also establishes the existence of the critical value 


3.1.2. Shannon Entropy
It is well known that the major way to appreciate the purity of a system is to study the evolution of its entropy. When this quantity tends to zero, we obtain a pure state. Decoherence stands for the loose of information in the system. This occurs when the exchange between the environment and the system affects the evolution of the concerned system. Mathematically, the entropy 
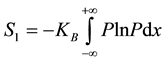
in which 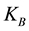


However, when
Figure 2. The 3D entropy for a simple harmonic oscillator with the parameters of Figure 1(a).
Figure 3. The 3D entropy as function of time and the system frequency for the parameters of Figure 1 with
frequency

3.2. System Properties for a Double Gaussian Case
In this section, we focus our attention on the study of the effects of the double Gaussian approximation function on
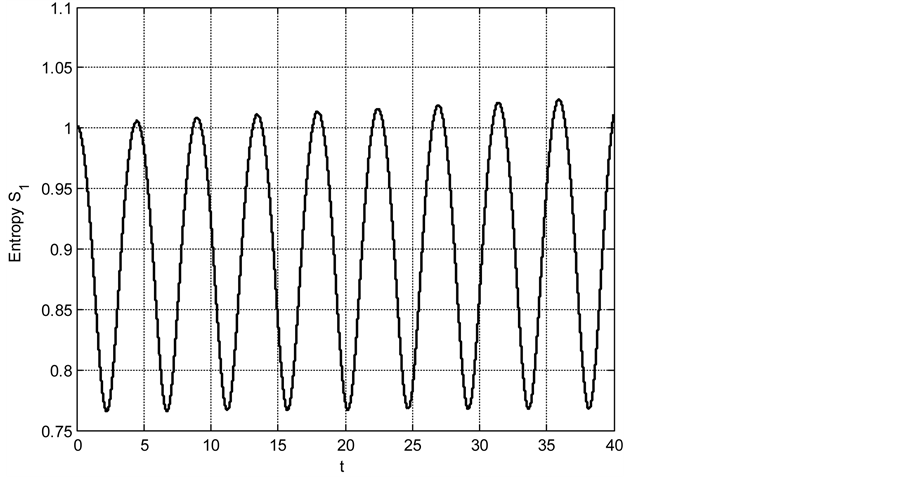

Figure 4. Behavior of the Shannon entropy 


the interaction between our damped harmonic oscillator and its environment. For this purpose, the initial state for the double Gaussian wave function is given by [31]

in which d defines the distance between the top of the two successive waves in the double Gaussian state. To appreciate the impact of this new wave packet on the thermodynamic parameters of the system, we seek separately its distribution probability and Shannon entropy.
3.2.1. Distribution Probability
The corresponding distribution probability 

wherein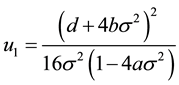



One could note that the distribution probability depends not only on time, position and system frequency, but also on the distance separating the two successive peaks of the double Gaussian function. In the limit case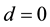
The Spatiotemporal evolution of the probability (17) is plotted on Figure 5. These figures confirm the fact that, the probability grows with the increment of the damped factor 

3.2.2. Shannon Entropy
In this subsection, we investigate the Shannon entropy relates to the double Gaussian wave function for a specific damped harmonic oscillator. Owing to the definition, this entropy is:

in which the probability 
First, Figure 6 presents the effects of the distance 

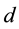

Next, we examine the influence of the damped factor 




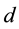





Figure 5. Distribution probability versus space and time for a double Gaussian wave function with the parameters


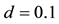
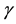

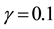
4. Conclusions
In this paper, we have examined the dynamics of the modified damped harmonic oscillator constructed from the Caldirola-Kanaï model and based on the idea of Bateman. For this purpose, the Feynman path integral method has been used to investigate the time dependent probability and the entanglement entropy exploiting the single and double Gaussian initial states. In these two initial states, we have shown that the Shannon entropy decreases with the system frequency and grows with the others parameters (such as time or damped factor). For both cases, we have established that the distribution probability possesses the same behavior. In the specific case of the double Gaussian approximation, we have obtained that the distribution probability and the Shannon’s entropy have been improved by the distance between two consecutive peaks of the wave.
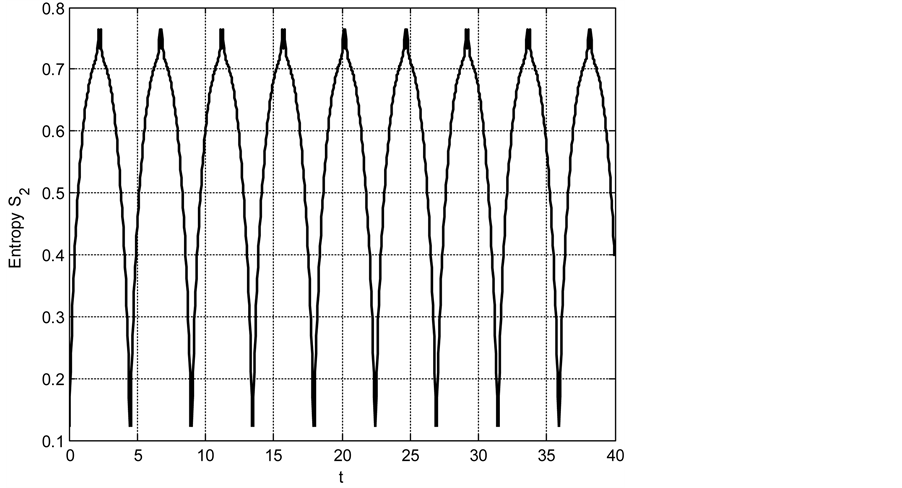

Figure 6. Shannon entropy 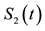

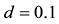

In the absence of the damped factor, we have recovered the results that link with the system in its pure state. Here, the information is exchanged periodically between the corresponding harmonic oscillator and the environment. For non-zero values of the damped factor, it has appeared that this transfer of information loses its periodicity traducing the loss of information in the system (decoherence phenomena). These results could be of great interest for engineering purposes since it becomes necessary to control the effects of the environment on the evolution of the system in order to reduce its decoherence. This phenomenon of controlling decoherence in an evolving system is essential in the construction of quantum computers that need the use of systems taken in their
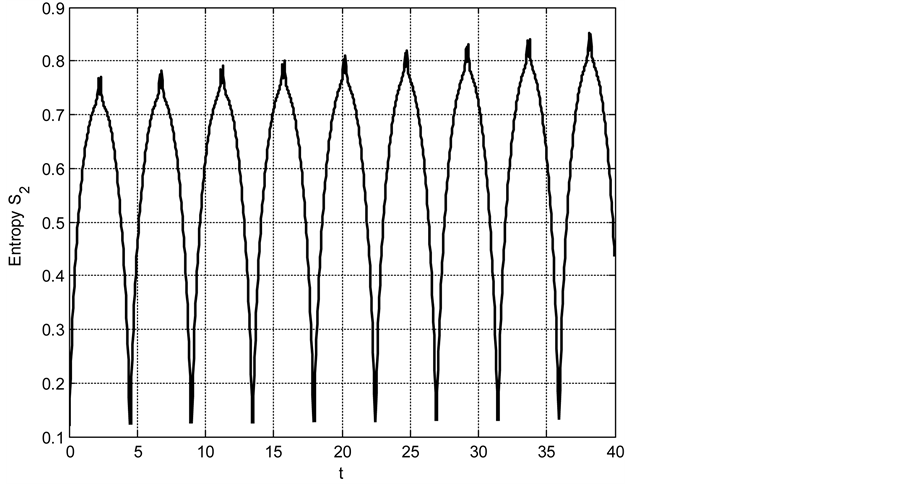

Figure 7. Temporal evolution of the Shannon entropy for the parameters of Figure 6 with 




different superposition states. Our study has also shown that such aim could be achieved by acting on the damped coefficient, the frequency of oscillation and/or the type of state as control parameter.
References
- Isar, A. (2005) Decoherence in Open Quantum Systems. Romanian Journal of Physics, 50, 147-156.
- Walls, D.F. and Millburn, G.J. (1994) Quantum Optics. Springer, Heildelberg.
- Scully, M.O. and Zubairy, M.S. (1997) Quantum Optics. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511813993
- Sargent III, M., Scully, M.O. and Lamb Jr., W.E. (1974) Laser Physics. Addison-Wesley, Reading.
- Nielsen, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University, Cam- bridge, UK.
- Karlsson, E.B. (1998) Coherence and Decoherence of Positive Particle States in Solids. Physica Scripta, 76, 179. http://dx.doi.org/10.1238/Physica.Topical.076a00179
- Chatzidimitriou-Dreismann, C.A., Abdul-Redah, T. and Kolaric, B. (2001) Entanglement of Protons in Organic Molecules: An Attosecond Neutron Scattering Study of C [Bond] H Bond Breaking. Journal of the American Chemical Society, 123, 11945-11951. http://dx.doi.org/10.1021/ja004186d
- Chatzidimitriou-Dreismann, C.A., Abdul Redah, T., Streffer, R.M. and Mayers, J. (1997) Anomalous Deep Inelastic Neutron Scattering from Liquid H2O-D2O: Evidence of Nuclear Quantum Entanglement. Physical Review Letters, 79, 2839-2842. http://dx.doi.org/10.1103/PhysRevLett.79.2839
- Krzywicki, A. (1993) Coherence and Decoherence in Radiation off Colliding Heavy Ions. Physical Review D, 48, 5190-5195. http://dx.doi.org/10.1103/PhysRevD.48.5190
- Zeh, H.D. (1986) Emergence of a Classical Universe from Quantum Gravity and Cosmology. Physics Letters A, 116, 9-12. http://dx.doi.org/10.1016/0375-9601(86)90346-4
- Zeh, H.D. (1988) Time in Quantum Gravity. Physics Letters A, 126, 311-317. http://dx.doi.org/10.1016/0375-9601(88)90842-0
- Zeh, H.D. (1992) The Physical Basis of the Direction of Time. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-02759-2
- Kiefer, C. (1987) Emergence of a Classical Universe from Quantum Gravity and Cosmology. Classical and Quantum Gravity, 4, 1369-1382. http://dx.doi.org/10.1088/0264-9381/4/5/031
- Halliwell, J. (1989) Decoherence in Quantum Cosmology. Physical Review D, 39, 2912-2923. http://dx.doi.org/10.1103/PhysRevD.39.2912
- Barvinsky, A.O. and Kamenshchik, A.Y. (1990) Preferred Basis in the Many-Worlds Interpretation of Quantum Mechanics and Quantum Cosmology. Classical and Quantum Gravity, 7, 2285-2293. http://dx.doi.org/10.1088/0264-9381/7/12/010
- Barvinsky, A.O. and Kamenshchik, A.Y. (1995) Preferred Basis in Quantum Theory and the Problem of Classicalizationof the Quantum Universe. Physical Review D, 52, 743-757. http://dx.doi.org/10.1103/PhysRevD.52.743
- Brandenberger, R., Laflamme, R. and Mijic, M. (1990) Modern Physics Letters A, 5, 2311.
- Paz, J.-P. and Sinha, S. (1991) Decoherence and Back Reaction: The Origin of the Semiclassical Einstein Equations. Physical Review D, 44, 1038-1049. http://dx.doi.org/10.1103/PhysRevD.44.1038
- Paz, J.-P. and Sinha, S. (1992) Decoherence and Back Reaction in Quantum Cosmology: Multidimensional Minisuperspace Examples. Physical Review D, 45, 2823-2842. http://dx.doi.org/10.1103/PhysRevD.45.2823
- Castagnino, M.A., Gangui, A., Mazzitelli, F.D. and Tkachev, I.I. (1993) Third Quantization, Decoherence and the Interpretation of Quantum Gravity in Mini-Super-Space. Classical and Quantum Gravity, 10, 2495-2504. http://dx.doi.org/10.1088/0264-9381/10/12/008
- Kefer, C. and Zeh, H.D. (1995) Arrow of Time in a Recollapsing Quantum Universe. Physical Review D, 51, 4145- 4153. http://dx.doi.org/10.1103/PhysRevD.51.4145
- Mensky, M.B. and Novikov, I.D. (1996) Decoherence Caused by Topology in a Time-Machine Spacetime. International Journal of Modern Physics D, 5, 1-27. http://dx.doi.org/10.1142/S0218271896000023
- Giulini, D., Joos, E., Kiefer, C., Kupsch, J., Stamatescu, I.O. and Zeh, H.D. (1996) Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-03263-3
- Paz, J.P. and Zurek, W.H. (2001) In Coherent Atomic Matter Waves. In: Kaiser, R., Westbrook, C. and David F., Eds., Les Houches Session LXXII, Springer, Berlin, 533-614.
- Zurek, W.H. (2003) Decoherence, Einselection, and the Quantum Origins of the Classical. Reviews of Modern Physics, 75, 715-775. http://dx.doi.org/10.1103/RevModPhys.75.715
- Morikawa, M. (1990) Quantum Decoherence and Classical Correlation in Quantum Mechanics. Physical Review D, 42, 2929-2932. http://dx.doi.org/10.1103/PhysRevD.42.2929
- Habib, S. and Laflamme, R. (1990) Wigner Function and Decoherence in Quantum Cosmology. Physical Review D, 42, 4056-4065. http://dx.doi.org/10.1103/PhysRevD.42.4056
- Alicki, R. (2004) Pure Decoherence in Quantum Systems. Open Systems & Information Dynamics (OSID), 11, 53-61. http://dx.doi.org/10.1023/B:OPSY.0000024755.58888.ac
- Joos, E., Zeh, H.D., Kiefer, C., Giulini, D., Kupsch, J. and Stamatescu, I.O. (2003) Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-05328-7
- Gamble, J.K. and Lindner, J.F. (2009) Demystifying Decoherence and the Master Equation of Quantum Brownian Motion. American Journal of Physics, 77, 244. http://dx.doi.org/10.1119/1.3043847
- Zuo, J. and O’Connell, R.F. (2004) Effect of an External Field on Decoherence: Part II. Journal of Modern Optics, 51, 821-832. http://dx.doi.org/10.1080/09500340408233599
- Ozcan, O., Akturk, E. and Sever, R. (2008) Time Dependence of Joint Entropy of Oscillating Quantum Systems. International Journal of Theoretical Physics, 47, 3207-3218. http://dx.doi.org/10.1007/s10773-008-9756-4
- Isar, A. (2007) Quantum Decoherence of a Damped Harmonic Oscillator. Optics and Spectroscopy, 103, 252-257. http://dx.doi.org/10.1134/S0030400X07080140
- Lindblad, G. (1976) Brownian Motion of a Quantum Harmonic Oscillator. Reports on Mathematical Physics, 10, 393- 406. http://dx.doi.org/10.1016/0034-4877(76)90029-X
- Sandulescu, A. and Scutaru, H. (1987) Open Quantum Systems and the Damping of Collective Models in Deep Inelastic Collisions. Annals of Physics, 173, 277-317. http://dx.doi.org/10.1016/0003-4916(87)90162-X
- Elran, Y. and Brumer, P. (2004) Decoherence in an Inharmonic Oscillator Coupled to a Thermal Environment: A Semi-Classical Forward-Backward Approach. The Journal of Chemical Physics, 121, 2673. http://dx.doi.org/10.1063/1.1766009
- Chruscinski, D. and Jurkowski, J. (2010) Memory in a Nonlocally Damped Oscillator. In: Accardi, L., Freudenberg, W. and Ohya, M., Eds., Quantum Bio-Informatics III, Tokyo University of Science, Tokyo, 155-166. http://dx.doi.org/10.1142/9789814304061_0014
- Bateman, H. (1931) On Dissipative Systems and Related Variational Principles. Physical Review, 38, 815-819. http://dx.doi.org/10.1103/PhysRev.38.815
- Caldirola, P. (1941) Quantum Analysis of Modified Caldirola-Kanai Oscillator Model for Electromagnetic Fieldsin Time-Varying. IL Nuovo Cimento, 18, 393-400. http://dx.doi.org/10.1007/BF02960144
- Feynman, R.P. (1948) Space-Time Approach to Non-Relativistic Quantum Mechanics. Reviews of Modern Physics, 20, 367-387. http://dx.doi.org/10.1103/RevModPhys.20.367
- Fai, L.C., Fomethe, A., Mborong, V.B., Fotue, A.J., Domngang, S., Issofa, N. and Tchoffo, M. (2008) Polaron State Screening by Plasmons in a Spherical Nanocrystal. Journal of Low Temperature Physics, 152, 71-87. http://dx.doi.org/10.1007/s10909-008-9803-9
- Um, C.I., Yeon, K.H. and George, T.F. (2002) The Quantum Damped Harmonic Oscillator. Physics Reports, 362, 63- 192. http://dx.doi.org/10.1016/S0370-1573(01)00077-1
- Um, C.I., Yeon, K.H. and Kahng, W.H. (1987) The Quantum Damped Driven Harmonic Oscillator. Journal of Physics A: Mathematical and General, 20, 611-626. http://dx.doi.org/10.1088/0305-4470/20/3/024
- Feynman, R.P. and Hibbs, A.R. (1965) Quantum Mechanics and Path Integrals. McGraw-Hill, New York.
NOTES
*Corresponding author.








