Journal of Quantum Information Science
Vol.4 No.2(2014), Article ID:46117,7 pages
DOI:10.4236/jqis.2014.42010
Local Implementations of Non-Local Quantum Gates in Linear Entangled Channel
Debashis Saha1, Sanket Nandan2, Prasanta K. Panigrahi1
1Indian Institute of Science Education and Research Kolkata, Mohanpur Campus, Nadia, India
2Indian Institute of Science Education and Research Pune, Pune, Maharashtra, India
Email: pprasanta@iiserkol.ac.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2014; revised 25 April 2014; accepted 14 May 2014
ABSTRACT
In this paper, we demonstrate
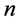 -party controlled unitary gate implementations locally
on arbitrary remote state through linear entangled channel where control parties
share entanglement with the adjacent control parties and only one of them shares
entanglement with the target party. In such a network, we describe the protocol
of simultaneous implementation of controlled-Hermitian gate starting from three
party scenarios. We also explicate the implementation of three party controlled-Unitary
gates, a generalized form of Toffoli gate and subsequently generalize the protocol
for
-party controlled unitary gate implementations locally
on arbitrary remote state through linear entangled channel where control parties
share entanglement with the adjacent control parties and only one of them shares
entanglement with the target party. In such a network, we describe the protocol
of simultaneous implementation of controlled-Hermitian gate starting from three
party scenarios. We also explicate the implementation of three party controlled-Unitary
gates, a generalized form of Toffoli gate and subsequently generalize the protocol
for
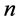 -party using minimal cost.
-party using minimal cost.
Keywords:Bell State, Controlled-Unitary Gate, Controlled-Hermitian Gate, Toffoli Gate

1. Introduction
One of the most striking features of the quantum world is entanglement. This esoteric quantum property has found practical use in the field of quantum information [1] . Qubit teleportation [2] [3] , superdense coding [4] , quantum information splitting [5] , secret sharing [6] , remote state preparation [7] [8] and many other quantum communication protocols have been theoretically and experimentally demonstrated taking recourse to entanglement. Local implementation of non-local quantum gates is another quantum communication protocol implementing a multi-partite quantum gate which can not be decomposed into individual local operations between spatially distributed qubits. This can be achieved using entangled channels shared by the remote parties and local operations with classical communications (LOCC). This quantum task is also called gate teleportation, which is necessary for distributed quantum computing.
As is well known, controlled-NOT (CNOT), together with the single qubit gate, form
the universal gates to which other gates can be decomposed
[9] . In principle, Controlled-Unitary gates can be implemented locally,
using only CNOT gate teleportation protocol. Involving less entanglement and communication
costs, several protocols have been proposed implementing non-local multi-partite
operations locally by LOCC using entangled channels [10]
-[21] and qubit communication
[22] [23] . Probabilistic and deterministic
gate implementation using non-maximally entangled state has been explicated [24] -[27] . Assisted with
linear optical manipulations, photon entanglement produced from parametric down-conversion,
and post-selection from the coincidence measurements, the CNOT gate has been teleported
experimentally [28] . Later, other experimental
protocols have been demonstrated [29] [30] . In contrast with the known protocols, we consider
here an arbitrary multipartite state, either product or entangled, where all the
qubits are remote placed and demonstrate the protocol of simultaneous and
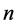 -qubit controlled operation in linear entangled channel.
-qubit controlled operation in linear entangled channel.
In the familiar network by Eisert-Jacobs-Papadopoulos-Plenio
[10] , each of the control parties shares one entangled state with the
target party and none of the control parties shares entanglement between them whereas
in linear entangled channel, the control parties share entanglement with the adjacent
control parties and only one of them shares entanglement with the target party.
As this network is linear, the target party has to maintain only one entangled channel,
which is particularly useful when the entanglement sharing is difficult between
each controlling agent with the target party. In this paper, we start with a three
party scenario, where Alice and Bob simultaneously implement controlled-Hermitian
![]() gate to Charlie in linear entangled network, which is then generalized for arbitrary
multi-partite state. Next section deals with the implementation of controlledcontrolled-Unitary
gate and the generalization to
gate to Charlie in linear entangled network, which is then generalized for arbitrary
multi-partite state. Next section deals with the implementation of controlledcontrolled-Unitary
gate and the generalization to
 -controlled Unitary gate implementation. Finally, we
conclude with directions for future work.
-controlled Unitary gate implementation. Finally, we
conclude with directions for future work.
2. Simultaneous Implementation of Controlled-Hermitian Gate
Consider three remote parties Alice, Bob and Charlie possess qubits 1, 4 and 7 respectively of the arbitrary state
![]() (1)
(1)
with![]() . Now Alice and Bob want to implement Controlled-Hermitian Gate
(as well as unitary) on Charlie’s system simultaneously where the target qubit is
common for both the control parties. To achieve this task, Alice and Bob share a
Bell state between their respective qubits 2 and 3; Bob and Charlie share a Bell
state between their respective qubits 5 and 6 :
. Now Alice and Bob want to implement Controlled-Hermitian Gate
(as well as unitary) on Charlie’s system simultaneously where the target qubit is
common for both the control parties. To achieve this task, Alice and Bob share a
Bell state between their respective qubits 2 and 3; Bob and Charlie share a Bell
state between their respective qubits 5 and 6 :
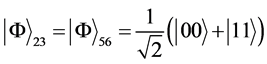 (2)
(2)
Here Alice shares entanglement with another control party and Bob shares entanglement with the target party, which makes a linear entanglement connection (shown in Figure 1). The combined state of all the qubits possessed by Alice, Bob and Charlie is given by,
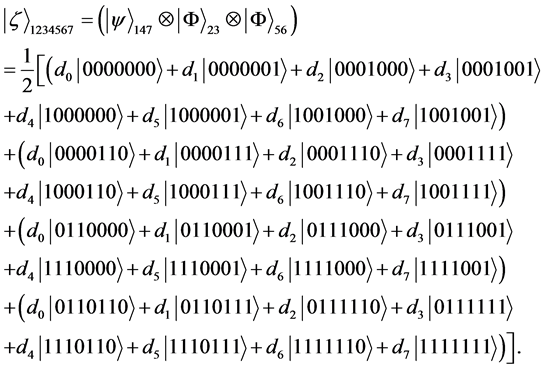 (3)
(3)
Step 2: Alice measures on qubit 2 in computational
basis and Bob applies local operations according to the outcomes of the measurements
as follows, (here
![]() are Pauli operators, with superscript “
are Pauli operators, with superscript “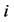 ” indicating the qubit operand;
” indicating the qubit operand;
![]() denotes controlled-Unitary gate, where “
denotes controlled-Unitary gate, where “ ” is the control bit and “
” is the control bit and “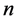 ” is target bit).
” is target bit).

Figure 1. Simultaneous implementation of Controlled-Hermitian gate through linear network.
The details protocol of simultaneous
 implementation through linear network is described belowStep 1: Alice first applies
controlled-NOT gate
implementation through linear network is described belowStep 1: Alice first applies
controlled-NOT gate
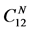 on her qubits 1 and 2.
on her qubits 1 and 2.
Step 3: Bob measures qubit 5 in computational basis and Charlie applies local operations according to the outcomes of the measurements as follows,
Step 4: Finally qubit 3 and 6 are measured in Hadamard basis by Bob and Charlie and corresponding Alice applies unitary operations to obtain the desired state.
The pictorial representation of local unitary operations, measurements and classical
communications of this protocol has been depicted in Figure
1. The simultaneous remote implementation of controlled-Hermitian gate from
two parties to one consumes 2 ebits and total 5 cbits to communicate the measurement
outcomes. The generalized protocol for
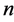 -party of simultaneous
-party of simultaneous
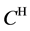 gate implementation described in Figure 2, is an
extension of the above protocol. For
gate implementation described in Figure 2, is an
extension of the above protocol. For
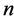 -party, the communication cost is
-party, the communication cost is
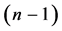 ebits and
ebits and
![]() cbits.
cbits.
From the above protocol, it can be inferred that the Unitary as well as Hermitian operators have significance in linear entangled network. This operator has the additional property of involution (i.e., the operator is same as its inverse), which is responsible for making this protocol deterministic. Most of the important gates like controlled-Pauli gates, controlled-Hadamard gate etc., belong to this category, making this implementation powerful.
3. Multiparty Controlled Unitary Gate Implementation
It has been shown that a more general form of Toffoli gate, i.e., controlled-controlled-Unitary gate can be deterministically implemented using two Bell pairs (2 ebits of entanglement) and 4 cbits to communicate the measurement outcomes [10] . Here, we demonstrate the implementation of this non-local gate with the same communication cost using linear entangled channel (shown in Figure 3). For illustration, we consider the same qubit distribution shared by Alice, Bob and Charlie described in Equation (3):
![]() (4)
(4)
where we want to implement controlled-controlled-Unitary gate,
![]() (here qubit 1 and 4 are control bits and qubit 7 is target bit)
on
(here qubit 1 and 4 are control bits and qubit 7 is target bit)
on![]() . The details of the protocol is illustrated belowStep 1: Alice
first applies controlled-NOT gate
. The details of the protocol is illustrated belowStep 1: Alice
first applies controlled-NOT gate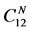 , on her two qubits.
, on her two qubits.
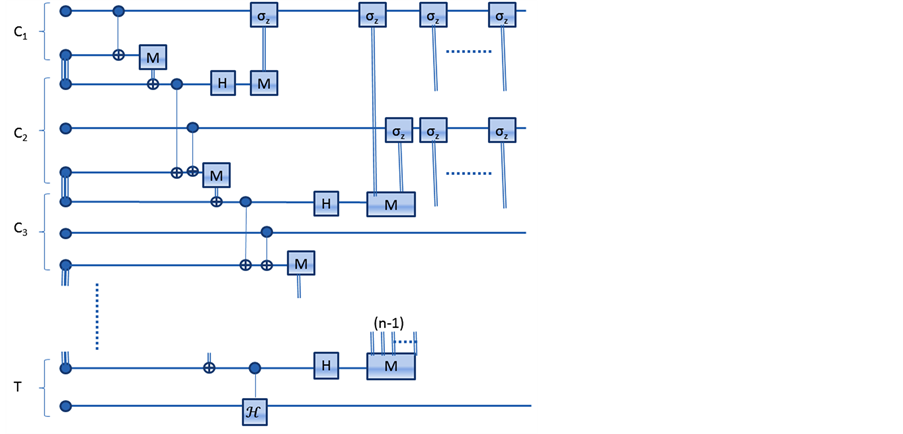
Figure 2. Simultaneous
implementation of n-party controlled hermitian gate through linear network (Here
 denotes the control parties and T denotes the target party).
denotes the control parties and T denotes the target party).

Figure 3. Controlled-controlled-Unitary gate implementation through linear network.
Step 3: Bob measures on qubit 5 in computational
basis and accordingly Charlie performs unitary gates, (here
 is denoted as
is denoted as![]() ).
).
Step 4: After that Charlie measures qubit 6 in Hadamard basis and Bob applies local operations depending on the outcomes.
Step 5: Finally qubit 3 is measured in Hadamard basis and Bob performs unitary gates to get the desired state which is shared by three parties.
The above procedure can be generalized to implement a
 -qubit gate, where
-qubit gate, where
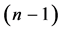 qubits are controls and the unitary operator acts on the target qubit, only if,
all the control qubits are
qubits are controls and the unitary operator acts on the target qubit, only if,
all the control qubits are
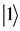 s. The protocol is illustrated in Figure
4 and for
s. The protocol is illustrated in Figure
4 and for
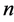 -party gate the communication cost is
-party gate the communication cost is
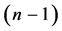 ebits and
ebits and
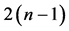 cbits which is optimal as shown in [10] .
cbits which is optimal as shown in [10] .
4. Conclusion
In conclusion, we have described non-local gate implementation protocols in linear
entanglement network by LOCC. Although the classical communication cost for implementing
simultaneous controlled-gate is more as compared to the scenario in [10] , the linear network is advantageous for large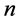 , as each party shares only two
, as each party shares only two
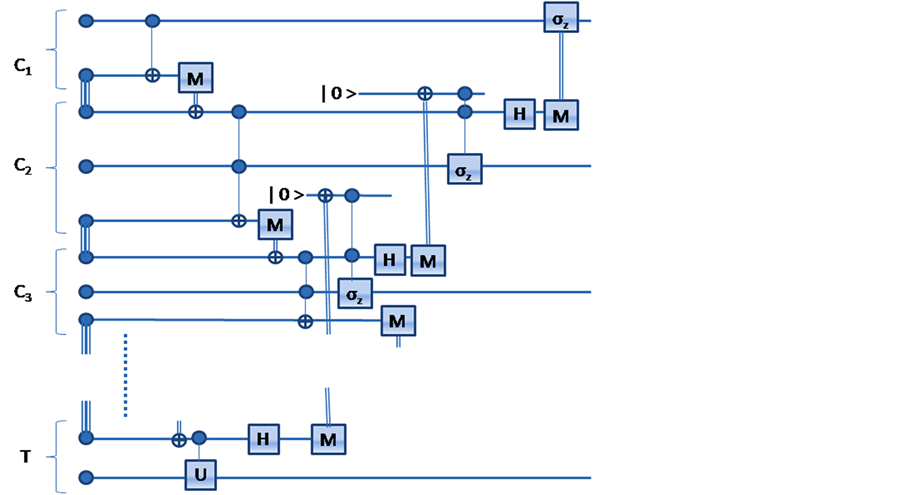
Figure 4. N party Controlled-Unitary gate implementation.
entangled states and the target as well as the first control party share one entangled state. The fact that, our network comprises of Bell states, which are realized in laboratory conditions, makes our protocol experimentally achievable [3] . Optimal protocol for the simultaneous controlled-Unitary and other non-local gate implementations in linear entangled channels can be further investigated.
Acknowledgements
The authors acknowledge Prof. Vijay A. Singh of Homi Bhabha Centre for Science Education (HBCSE-TIFR), Mumbai, India for continuous encouragement. This work is supported by the “National Initiative on Undergraduate Science” (NIUS) program, undertaken by HBCSE.
We acknowledge that summary of this work is presented as a poster in “Asian Quantum Information Science Conference 2013”.
References
- Nielsen, M.A. and Chuang, I.J. (2002) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge.
- Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A. and Wootters, W.K. (1993) Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Physical Review Letters, 70, Article ID: 1895. http://dx.doi.org/10.1103/PhysRevLett.70.1895
- Bouwmeester, D., Pan, J.W., Mattle, K., Eibl, M., Weinfurter, H. and Zeilinger, A. (1997) Experimental Quantum Teleportation. Nature (London), 390, 575-579. http://dx.doi.org/10.1038/37539
- Bennett, C.H. and Wiesner, S.J. (1992) Communication via One and Two Particle Operators on Einstein-Podolsky-Rosen States. Physical Review Letters, 69, 2881. http://dx.doi.org/10.1103/PhysRevLett.69.2881
- Bandyopadhyay, S. (2000) Teleportation and Secret Sharing with Pure Entangled States. Physical Review A, 62, Article ID: 012308. http://dx.doi.org/10.1103/PhysRevA.62.012308
- Hillery, M., Buzek, V. and Berthiaume, A. (1999) Quantum Secret Sharing. Physical Review A, 59, Article ID: 1829. http://dx.doi.org/10.1103/PhysRevA.59.1829
- Pati, A.K. (2000) Minimum Classical Bit for Remote Preparation and Measurement of a Qubit. Physical Review A, 63, Article ID: 014302. http://dx.doi.org/10.1103/PhysRevA.63.014302
- Bennett, C.H., Hayden, P., Leung, D.W., Shor, P.W. and Winter, A. (2005) Remote Preparation of Quantum States. IEEE Transactions on Information Theory, 51, 56-74. http://dx.doi.org/10.1109/TIT.2004.839476
- Barenco, A., Bennett, C.H., Cleve, R., DiVincenzo, D.P., Margolus, N., Shor, P., Sleator, T., Smolin, J.A. and Weinfurter, H. (1995) Elementary Gates for Quantum Computation. Physical Review A, 52, Article ID: 3457. http://dx.doi.org/10.1103/PhysRevA.52.3457
- Eisert, J., Jacobs, K., Papadopoulos, P. and Plenio, M.B. (2000) Optimal Local Implementation of Nonlocal Quantum Gates. Physical Review A, 62, Article ID: 052317. http://dx.doi.org/10.1103/PhysRevA.62.052317
- Collins, D., Linden, N. and Popescu, S. (2001) Nonlocal Content of Quantum Operations. Physical Review A, 64, Article ID: 032302. http://dx.doi.org/10.1103/PhysRevA.64.032302
- Dur, W. and Cirac, J.I. (2001) Nonlocal Operations: Purification, Storage, Compression, Tomography, and Probabilistic Implementation. Physical Review A, 64, Article ID: 012317. http://dx.doi.org/10.1103/PhysRevA.64.012317
- Chefles, A., Gilson, C.R. and Barnett, S.M. (2001) Entanglement, Information, and Multiparticle Quantum Operations. Physical Review A, 63, Article ID: 032314. http://dx.doi.org/10.1103/PhysRevA.63.032314
- Cirac, J.I., Dur, W., Kraus, B. and Lewenstein, M. (2001) Entangling Operations and Their Implementation Using a Small Amount of Entanglement. Physical Review Letters, 86, Article ID: 544. http://dx.doi.org/10.1103/PhysRevLett.86.544
- Ye, M.Y., Zhang, Y.S. and Guo, G.C. (2006) Efficient Implementation of Controlled Rotations by Using Entanglement. Physical Review A, 73, Article ID: 032337. http://dx.doi.org/10.1103/PhysRevA.73.032337
- Berry, D.W. (2007) Implementation of Multipartite Unitary Operations with Limited Resources. Physical Review A, 75, Article ID: 032349. http://dx.doi.org/10.1103/PhysRevA.75.032349
- Wang, A.M. (2007) Combined and Controlled Remote Implementations of Partially Unknown Quantum Operations of Multiqubits Using Greenberger-Horne-Zeilinger States. Physical Review A, Article ID: 75, Article ID: 062323. http://dx.doi.org/10.1103/PhysRevA.75.062323
- Dang, G.F. and Fan, H. (2008) Remote Controlled-Not Gate of d-Dimension. e-print arXiv:quant-ph/0711.3714v2.
- Yu, L., Griffths, R.B. and Cohen, S.M. (2010) Efficient Implementation of Bipartite Nonlocal Unitary Gates Using Prior Entanglement and Classical Communication. Physical Review A, 81, Article ID: 062315. http://dx.doi.org/10.1103/PhysRevA.81.062315
- Cohen, S.M. (2010) Optimizing Local Protocols for Implementing Bipartite Nonlocal Unitary Gates Using Prior Entanglement and Classical Communication. Physical Review A, 81, Article ID: 062316. http://dx.doi.org/10.1103/PhysRevA.81.062316
- Stahlke, D. and Griffiths, R.B. (2011) Entanglement Requirements for Implementing Bipartite Unitary Operations. Physical Review A, 84, Article ID: 032316. http://dx.doi.org/10.1103/PhysRevA.84.032316
- Zhou, X., Leung, D.W. and Chuang, I.L. (2000) Methodology for Quantum Logic Gate Construction. Physical Review A, 62, Article ID: 052316. http://dx.doi.org/10.1103/PhysRevA.62.052316
- Yang, C.P. (2008) A New Protocol for Constructing Nonlocal n-Qubit Controlled-U Gates. Physical Review A, 372, 1380-1386.http://dx.doi.org/10.1016/j.physleta.2007.09.048
- Jang, J., Lee, J., Kim, M.S. and Park, Y.J. (2001) Probabilistic Nonlocal Gate Operation via Imperfect Entanglement. e-print arXiv:quant-ph/0101107v1.
- Chen, L. and Chen, Y.X. (2005) Probabilistic Implementation of a Nonlocal Operation Using a Nonmaximally Entangled State. Physical Review A, 71, Article ID: 054302. http://dx.doi.org/10.1103/PhysRevA.71.054302
- Groisman, B. and Reznik, B. (2005) Implementing Nonlocal Gates with Nonmaximally Entangled States. Physical Review A, 71, Article ID: 032322. http://dx.doi.org/10.1103/PhysRevA.71.032322
- Yao, C.M. and Cao, B.F. (2009) Efficient Implementation of a Nonlocal Gate with Nonmaximal Entanglement. Physical Review A, 373, 1011-1014. http://dx.doi.org/10.1016/j.physleta.2009.01.039
- Huang, Y.F., Ren, X.F., Zhang, Y.S., Duan, L.M. and Guo, G.C. (2004) Experimental Teleportation of a Quantum Controlled-Not Gate. Physical Review Letters, 93, Article ID: 240501. http://dx.doi.org/10.1103/PhysRevLett.93.240501
- Huelga, S.F., Plenio, M.B., Xiang, G.Y., Li, J. and Guo, G.C. (2005) Remote Implementation of Quantum Operations. Journal of Optics B Quantum and Semiclassical Optics, 7, S384. http://dx.doi.org/10.1088/1464-4266/7/10/026
- Xia, Y., Song, J. and Song, H.S. (2008) Controlled Local Implementation of Nonlocal Operations. Journal of Modern Optics, 55, 3063-3070. http://dx.doi.org/10.1080/09500340802331856


