Journal of Quantum Information Science
Vol.3 No.2(2013), Article ID:32936,7 pages DOI:10.4236/jqis.2013.32012
Quantum Simulation of 2p-π Electronic Hamiltonian in Molecular Ethylene by Using an NMR Quantum Computer
Department of Physics, Faculty of Arts and Sciences, Ondokuz Mayıs University, Samsun, Turkey
Email: *dturkpence@omu.edu.tr
Copyright © 2013 Deniz Türkpençe, Azmi Gençten. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 1, 2013; revised May 8, 2013; accepted May 23, 2013
Keywords: NMR Quantum Computer; Quantum Simulation; Molecular Ethylene; ASP; IPEA
ABSTRACT
Classical simulation of a quantum system is a hard problem. It’s known that these problems can be solved efficiently by using quantum computers. This study demonstrates the simulation of the molecular Hamiltonian of 2p-π electrons of ethylene in order to calculate the ground state energy. The ground state energy is estimated by an iterative phase estimation algorithm. The ground state is prepared by the adiabatic state preparation and the implementation of the procedure is carried out by numerical simulation of two-qubit NMR quantum simulator. The readout scheme of the simulator is performed by extracting binary bits via NMR interferometer.
1. Introduction
Quantum information processing has become one of the most interesting fields in science and technology [1]. It has a potential to change the technology towards to quantum technology [2]. In 1982, Feynman proposed that simulation of quantum systems can be efficiently achieved by using computers working with the quantum mechanical principles [3]. First David Deutsch considered a computer device based on quantum mechanical principles [4]. Then other experimental and theoretical studies are performed on quantum information processing [5,6]. Seth Lloyd defined quantum computers as universal quantum simulators by recalling Feynman’s original motivation for introducing quantum computers [7]. The classification of quantum simulation is separated into two main lines. One of them is simulating a target quantum system by using another quantum system and the latter is simulating the target quantum system by constructing the elements of the target Hamiltonian with unitary and universal quantum logic gates [8].
With mature quantum control methods, NMR is an excellent test bed of physical implementations of quantum computing. Some physical systems examined by quantum simulations in the framework of NMR methods are reported elsewhere [9-13]. For quantum chemistry problems many approximation methods and software packages are developed since the difficulty of the problem scales exponentially with the system size. But it’s known that quantum computers promise efficient algorithms in order to simulate and prepare quantum states and find eigenvalues in polynomial time [14,15]. In order to calculate molecular energies, phase estimation algorithm is used by Guzik et al. [16]. In this algorithm the energy information can be extracted by phase kick-backs. For eigenstate preparations, Adiabatic State Preparation (ASP) is also proposed by Guzik et al. [16]. ASP exploits the quantum adiabatic theory in order to simulate the ground state of the desired system. Once the ground state is prepared, the ground state energy information can be extracted via relative phases by the phase estimation procedure. Recent studies about quantum simulations of quantum chemistry problems can be found elsewhere [18-23]. For experimental implementations, iterative phase estimation algorithm (IPEA) is developed in order to reduce the number of qubits [24]. NMR techniques provide efficient ways to optimize the adiabatic procedure for ground state preparation [25].
This study performs a numerical simulation of the quantum simulation of 2p-p electronic Hamiltonian in molecular ethylene on an NMR quantum computer. In quantum simulation an iterative phase estimation algorithm (IPEA) is used for the calculation of the ground state energy [24]. Ground state is prepared by ASP [25]. The goal of this study is to present a quantum simulation procedure for a better understanding of IPEA and ASP algorithms with NMR techniques. This manuscript is organized as follows. Section 2 explains a brief introduction to the theory about the problem Hamiltonian and the ground state energy calculation process. Definition of the problem and it’s solution methods can be found in Section 3. Results and discussion are presented in Section 4. Conclusion of the study is given in Section 5.
2. Theory
The aim of classical simulation of a system is to obtain the final state by solving the differential equations which governs the dynamical behaviors of the system with known initial conditions. Since the number of differential equations increase exponentially with the system size, it’s inefficient to simulate quantum systems with classical computers.
The goal of quantum simulation is to use quantum systems to simulate other quantum systems in order to achieve the simulation process efficiently. The evolutions of quantum systems are expressed by the second postulate of quantum mechanics as
 (1)
(1)
Where  is the system Hamiltonian. The challenge of quantum simulation is to discrete the system hamiltonian
is the system Hamiltonian. The challenge of quantum simulation is to discrete the system hamiltonian  by a set of unitary operators as
by a set of unitary operators as
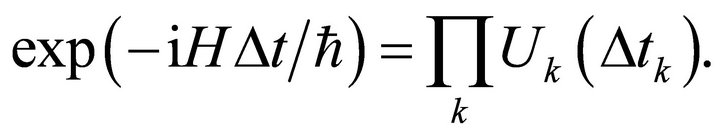 (2)
(2)
Where  is the total time of simulation process. Generally
is the total time of simulation process. Generally  is hard to exponentiate and first, second or higher orders of approximations are possible for splitting the operator [1].The energy for
is hard to exponentiate and first, second or higher orders of approximations are possible for splitting the operator [1].The energy for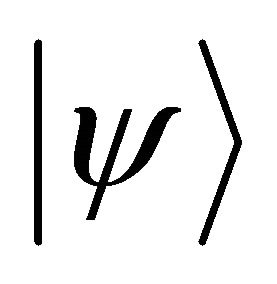 state which is prepared by a universal quantum computer can be obtained by a phase estimation algorithm [14,16]. The unitary operator
state which is prepared by a universal quantum computer can be obtained by a phase estimation algorithm [14,16]. The unitary operator 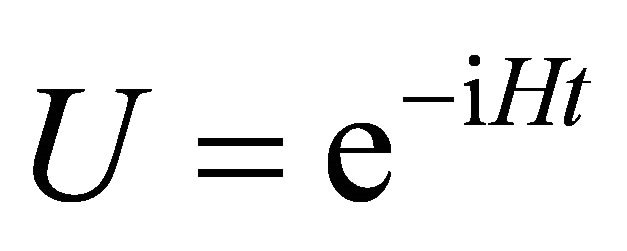 is applied as a controlled fashion to
is applied as a controlled fashion to 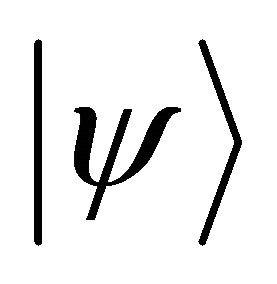 in the target register:
in the target register:
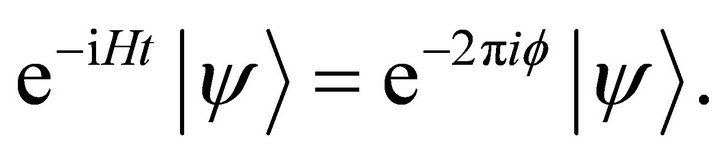 (3)
(3)
Where 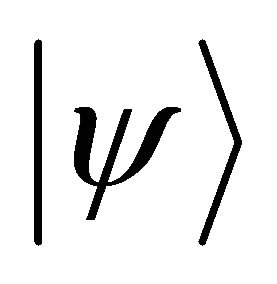 is an eigenstate of
is an eigenstate of . In the eigenvalue equation above, energy is encoded in phase as
. In the eigenvalue equation above, energy is encoded in phase as
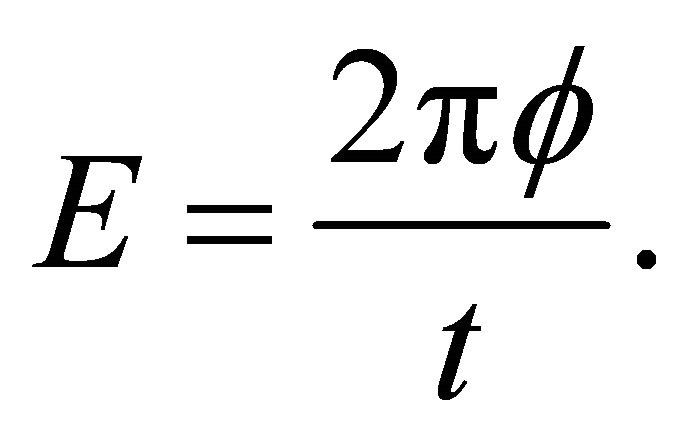 (4)
(4)
Where t can be chosen arbitrarily in which  ranges from 0 to 1. Finally an inverse quantum Fourier transform is applied the first register before the measurement process [16].
ranges from 0 to 1. Finally an inverse quantum Fourier transform is applied the first register before the measurement process [16].
2.1. The Hamiltonian
For the molecular Hamiltonian of ethylene 2p-π electrons, we adopt the notation used elsewhere [26]:
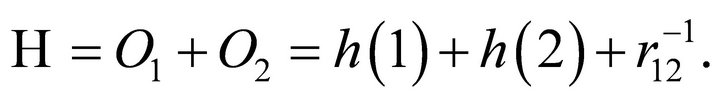 (5)
(5)
Where 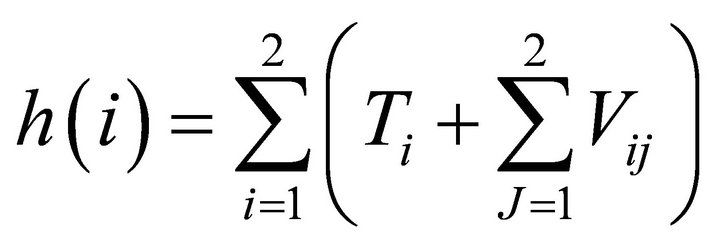 is the core Hamiltonian for
is the core Hamiltonian for
 electron and
electron and  is the coulomb potential energy between two electrons.
is the coulomb potential energy between two electrons.
To obtain the Hamiltonian and calculate electronic energies as functions of configuration, we choose a truncated basis set which is a standard approach for quantum chemistry calculations. In our simple case we don’t need Hartree-Fock procedure to determine spin orbitals because we obtain four spin orbitals by symmetry as
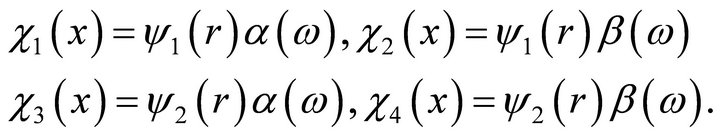 (6)
(6)
Where 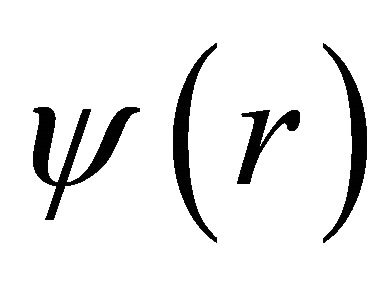 is the spatial function and
is the spatial function and 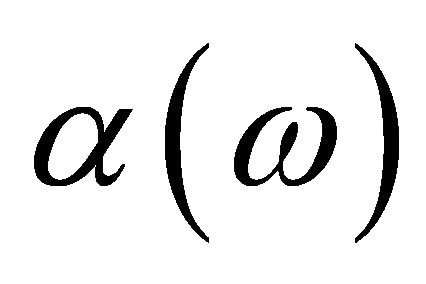 and
and  are spin functions. By using 4 spin orbitals and 2 electrons, there are
are spin functions. By using 4 spin orbitals and 2 electrons, there are 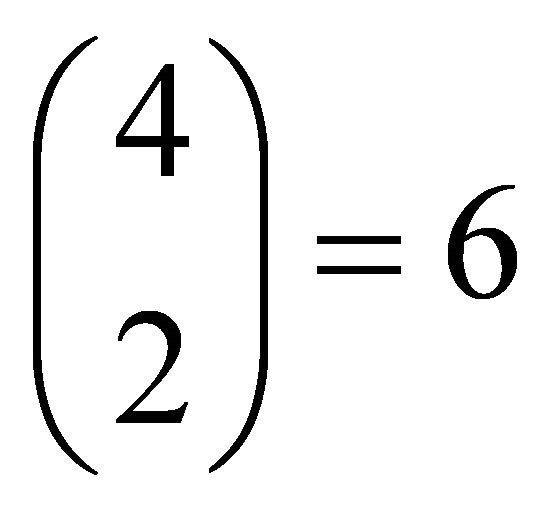 different configurations. By evaluating the symmetry, just two determinants, ground state
different configurations. By evaluating the symmetry, just two determinants, ground state  and doubly excited state
and doubly excited state 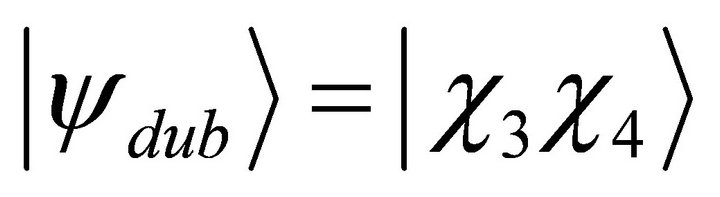 appear in the calculations. As the first step of the simulation process the ground and the doubly exited states are mapped to computational basis as
appear in the calculations. As the first step of the simulation process the ground and the doubly exited states are mapped to computational basis as . By these considerations a Full Configuration Interaction (FCI) Hamiltonian matrix is [26]
. By these considerations a Full Configuration Interaction (FCI) Hamiltonian matrix is [26]
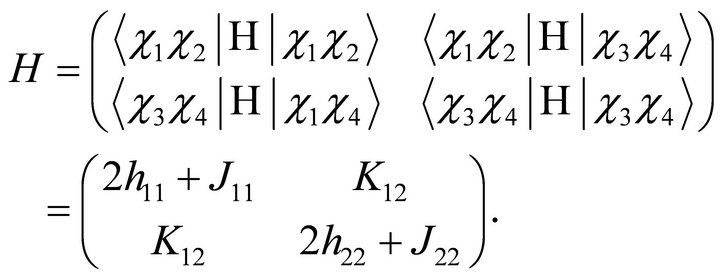 (7)
(7)
Where 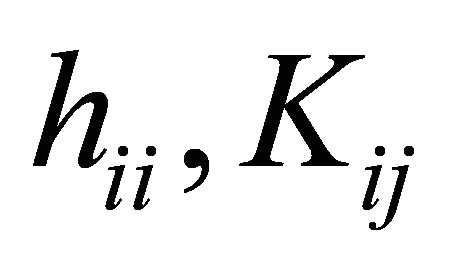 and
and  are one electron integrals, exchange integrals and coulomb integrals respectively.
are one electron integrals, exchange integrals and coulomb integrals respectively.
2.2. IPEA and the State Preparation
IPEA is used to reduce the number of qubits and operations in obtaining the eigenvalues. The form of an IPEA is presented in Figure 1 [24]. The information will be extracted by the top qubit which is prepared as 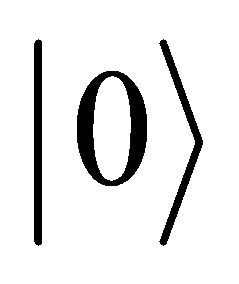 and the lower one prepared as
and the lower one prepared as  which is the eigenstate wave function of
which is the eigenstate wave function of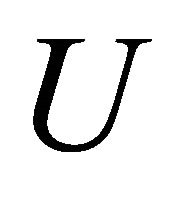 . The unitary operation
. The unitary operation  is applied as controlled operation and it obeys Equation (1). For a two qubit example after hadamard and controlled operations, the state becomes
is applied as controlled operation and it obeys Equation (1). For a two qubit example after hadamard and controlled operations, the state becomes
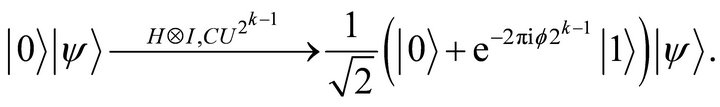 (8)
(8)
Where 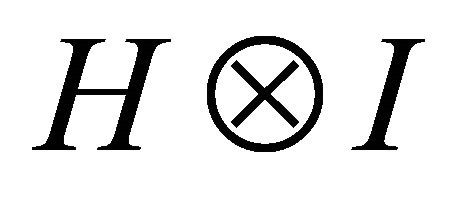 implies the hadamard operation in the first qubit and the phase
implies the hadamard operation in the first qubit and the phase  is defined in the binary ex-
is defined in the binary ex-
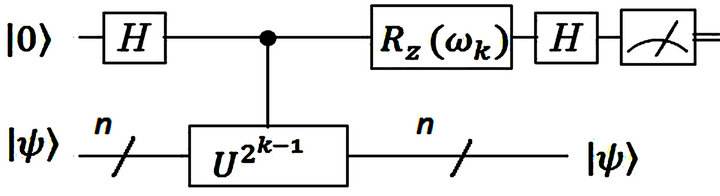
Figure 1. The kth iteration in IPEA. Iteration starts with k = m backwards to k = 1 [24].
pansion as 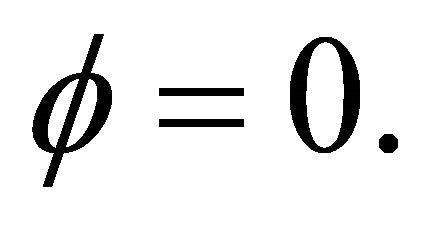
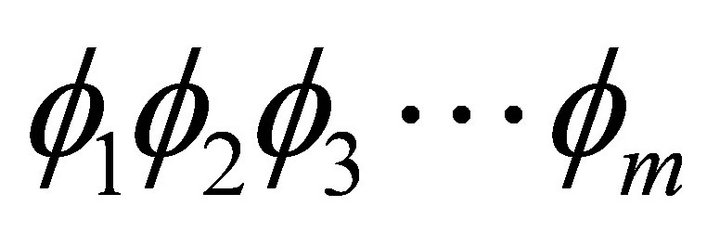 with no more than m bits. In the first iteration
with no more than m bits. In the first iteration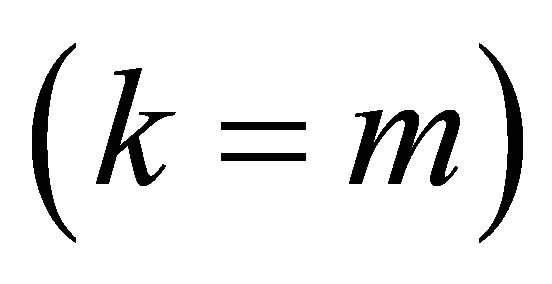 , the
, the 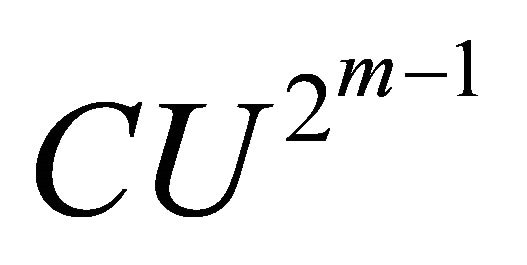 gate is applied and
gate is applied and  bit is extracted deterministically. Then
bit is extracted deterministically. Then  bit is extracted by the next iteration
bit is extracted by the next iteration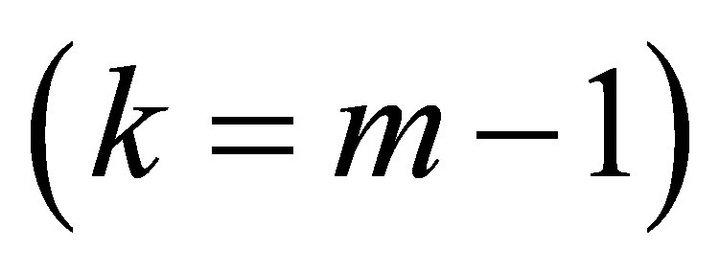 . This iteration is performed by the previous bit information and a conjugated Z rotation with the angle of
. This iteration is performed by the previous bit information and a conjugated Z rotation with the angle of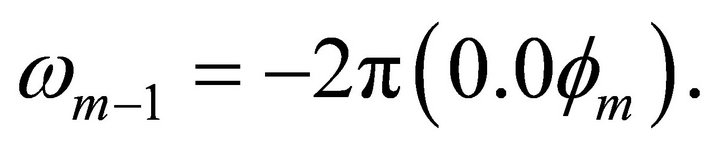 Information is transferred through this
Information is transferred through this  rotation which is called a feedback operation. So the less significant bits are extracted first and then by evaluating the extracted information more significant bits are obtained.
rotation which is called a feedback operation. So the less significant bits are extracted first and then by evaluating the extracted information more significant bits are obtained.
The ground state wave function  can be prepared by some number of operations by exploiting adiabatic theorem. According to adiabatic theorem, the system will remain in its ground state if the Hamiltonian varies slowly enough and if there is a gap between the ground state and the first excited state [17]. The adiabatic evolution of the Hamiltonian as a function of implementation steps (m) can be stated as [25]
can be prepared by some number of operations by exploiting adiabatic theorem. According to adiabatic theorem, the system will remain in its ground state if the Hamiltonian varies slowly enough and if there is a gap between the ground state and the first excited state [17]. The adiabatic evolution of the Hamiltonian as a function of implementation steps (m) can be stated as [25]
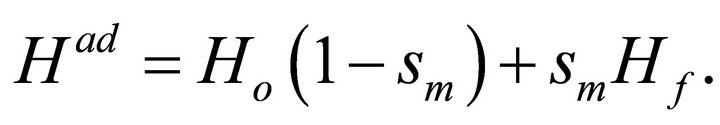 (9)
(9)
Where 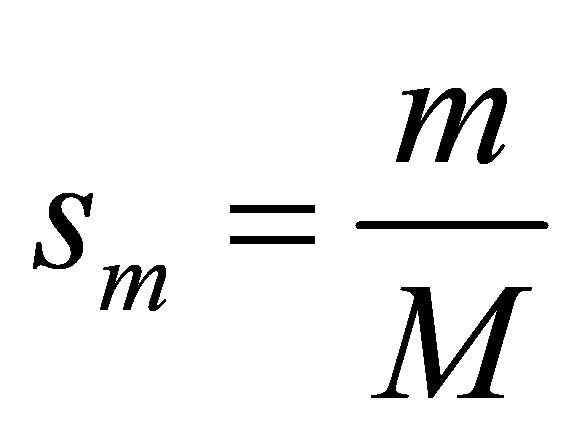 and M is the number of steps,
and M is the number of steps, 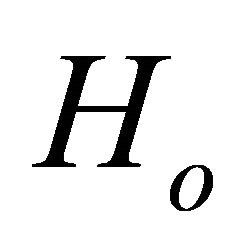 is the initial Hamiltonian and
is the initial Hamiltonian and 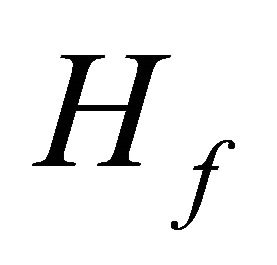 is the problem Hamiltonian. For a realistic operator implementation of this Hamiltonian as
is the problem Hamiltonian. For a realistic operator implementation of this Hamiltonian as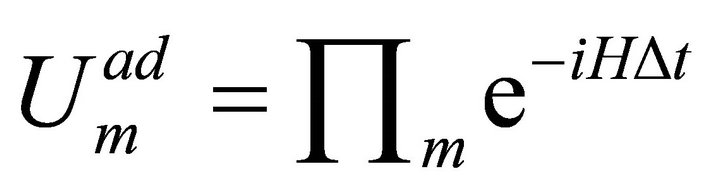 , one can use TrotterSuzuki Formulato parse the steps as;
, one can use TrotterSuzuki Formulato parse the steps as;
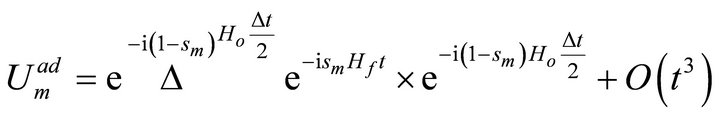 [1]. Where
[1]. Where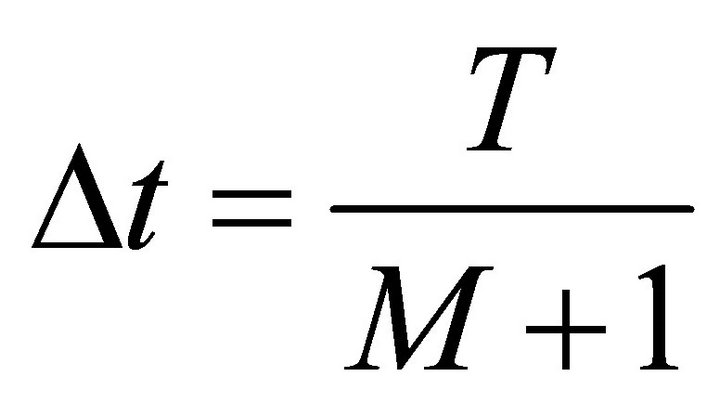 ,
, 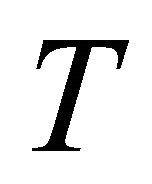 is the total time of the adiabatic evolution and
is the total time of the adiabatic evolution and 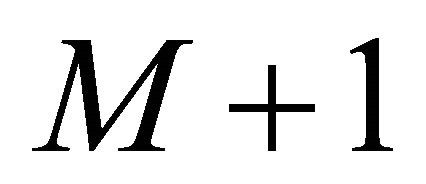 is the total number of steps.
is the total number of steps.
3. Ethylene 2p-π Electrons Problem
The FCI Hamiltonian matrix for ethylene 2p-π electrons can be constructed by evaluating the integrals indicated above. The elements of the problem matrix can be constructed as 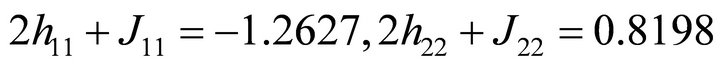 and
and  in a.u. [27]. The problem is to present the calculation of the ground state energy of the Hamiltonian by a two qubit NMR quantum computer. The calculated result can be compared with the theoretical one which is the lowest eigenvalue of the problem matrix. Chloroform molecule was chosen as two-qubit NMR quantum register and initialized for the experiment [28,29]. Here, proton
in a.u. [27]. The problem is to present the calculation of the ground state energy of the Hamiltonian by a two qubit NMR quantum computer. The calculated result can be compared with the theoretical one which is the lowest eigenvalue of the problem matrix. Chloroform molecule was chosen as two-qubit NMR quantum register and initialized for the experiment [28,29]. Here, proton 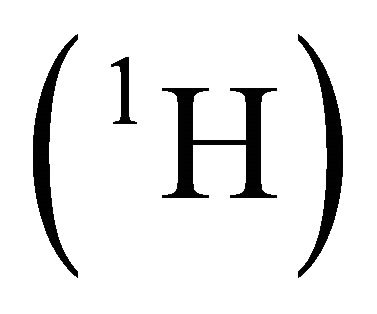 nucleus is assumed to be the probe qubit in which the energy information will be extracted. And the carbon
nucleus is assumed to be the probe qubit in which the energy information will be extracted. And the carbon 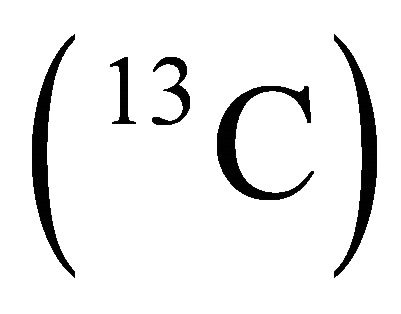 nucleus is the system qubit in which the simulation will take place.
nucleus is the system qubit in which the simulation will take place.
The calculation procedure will be carried out by an IPEA as seen in Figure 1. Here we see a controlled operation 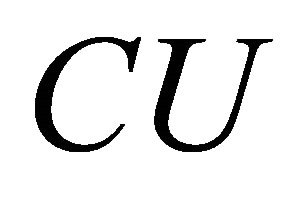 where
where 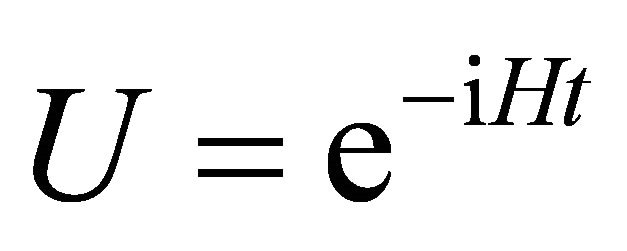 acts on
acts on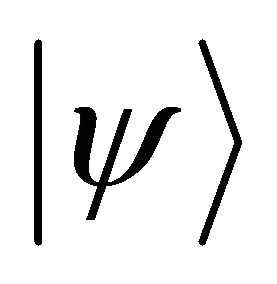 .
.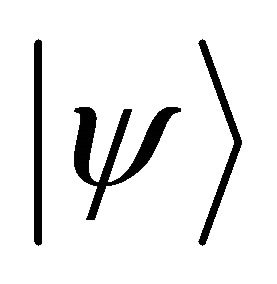 is the ground state of ethylene 2p-π electrons system and
is the ground state of ethylene 2p-π electrons system and  is the system hamiltonian. The energy information will be encoded by the extracted phase
is the system hamiltonian. The energy information will be encoded by the extracted phase  by
by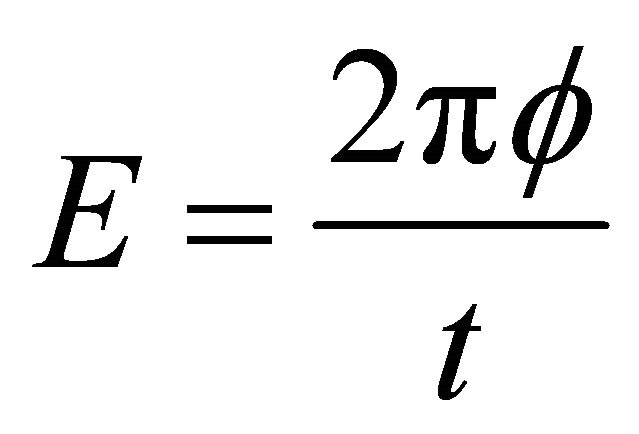 . We obtain this phase by
. We obtain this phase by 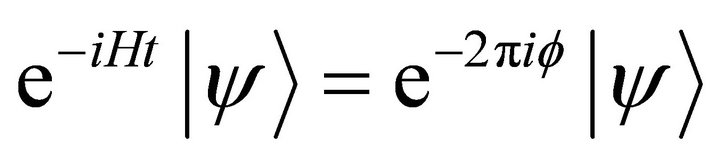 eigenvalue equation. To justify this equation the ground state of the system should be prepared before the controlled operation. Then the first step of the problem is to prepare the ground state of the system. As addressed before, ASP procedure will be used to prepare the ground state. The ASP process will be carried out by NMR techniques [25]. According to the ASP process, the initial Hamiltonian
eigenvalue equation. To justify this equation the ground state of the system should be prepared before the controlled operation. Then the first step of the problem is to prepare the ground state of the system. As addressed before, ASP procedure will be used to prepare the ground state. The ASP process will be carried out by NMR techniques [25]. According to the ASP process, the initial Hamiltonian 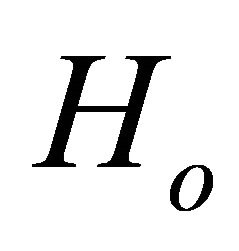 should be altered slowly towards target Hamiltonian
should be altered slowly towards target Hamiltonian  by Equation (9). The target hamiltonian can be obtained easily in terms of pauli operators by substituting the integral values given above into the problem matrix in Equation (7). On the other hand the initial state of the system qubit should be the superposition of the ground state
by Equation (9). The target hamiltonian can be obtained easily in terms of pauli operators by substituting the integral values given above into the problem matrix in Equation (7). On the other hand the initial state of the system qubit should be the superposition of the ground state 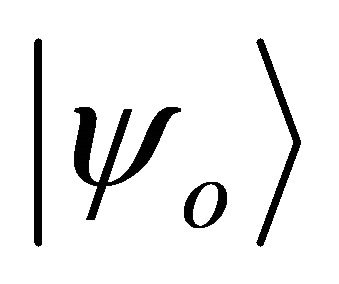 and the doubly excited state
and the doubly excited state 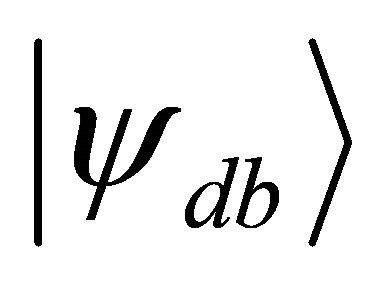 as
as
 to fulfill the initialization condition of the adiabatic process. This state can be obtained by applying a
to fulfill the initialization condition of the adiabatic process. This state can be obtained by applying a 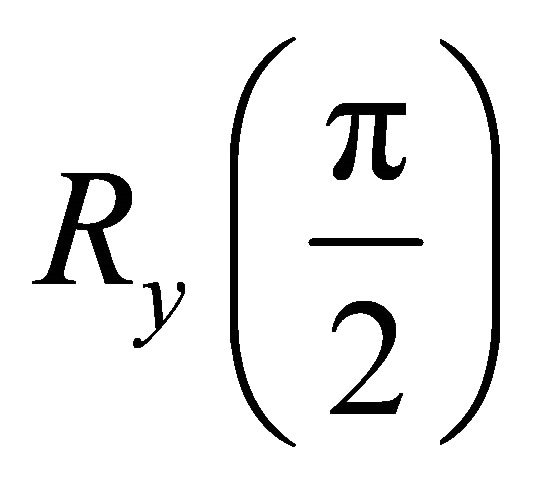 NMR pulse to the system qubit
NMR pulse to the system qubit
 which initially has a local natural Hamiltonian
which initially has a local natural Hamiltonian
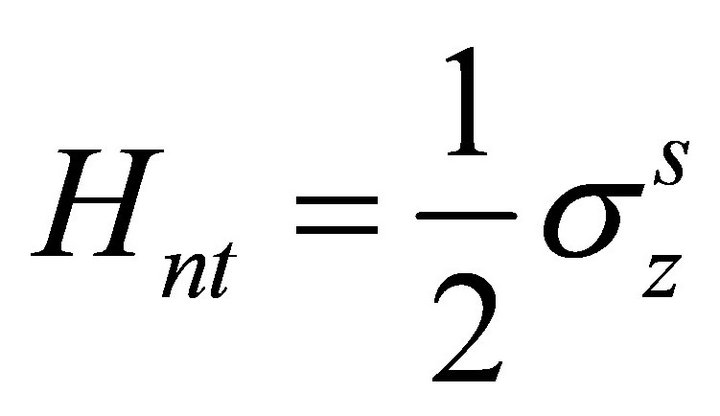 . Thus the initial hamiltonian is
. Thus the initial hamiltonian is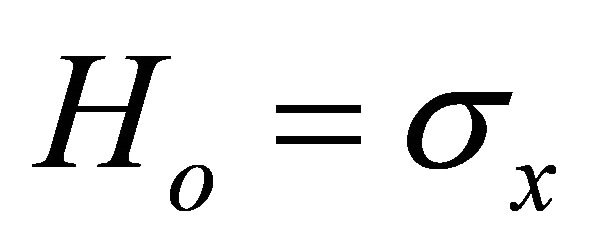 .
.
Figure 2 illustrates ground state simulation of the system qubit. The evolution of the initial Hamiltonian to the final Hamiltonian
to the final Hamiltonian 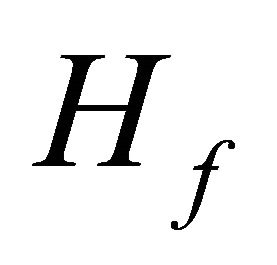 should not be like a sudden jump as shown in Figure 2(a) but it should be a slow variation in which the adiabatic condition entails. This slow adiabatic variation of the system hamiltonian can be carried out by composite pulses
should not be like a sudden jump as shown in Figure 2(a) but it should be a slow variation in which the adiabatic condition entails. This slow adiabatic variation of the system hamiltonian can be carried out by composite pulses  which are well known by NMR platform [30].
which are well known by NMR platform [30].
Since the algorithm explained in Figure 1 will be implemented by an NMR quantum computer, all unitary operators should be carried out by radio frequency (rf) pulses. In order to construct the controlled operation in terms of rf pulses, the methods are adopted from elsewhere [30]. The ground state energy information of the system which is encoded in the relative phases should be extracted by binary digits since the computational bases
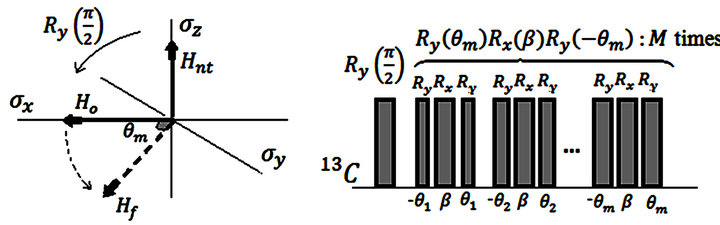
Figure 2. Ground state simulation of the system qubit. (a) vector illustration of system Hamiltonian. The initial Hamiltonian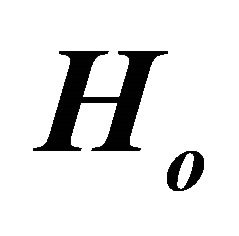 will be interpolated smoothly by ASP to
will be interpolated smoothly by ASP to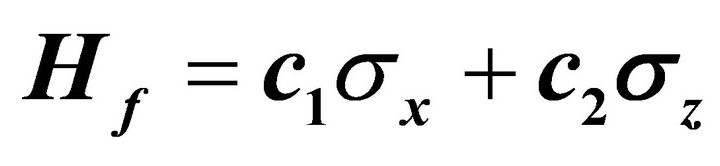 ; (b) ASP process with NMR pulses. Here
; (b) ASP process with NMR pulses. Here ,
,  is the total time of the adiabatic evolution and
is the total time of the adiabatic evolution and  is the number of steps. We take
is the number of steps. We take  and
and 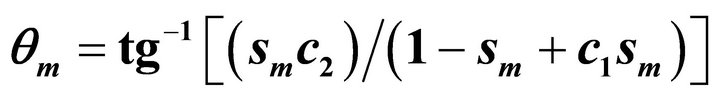 where
where 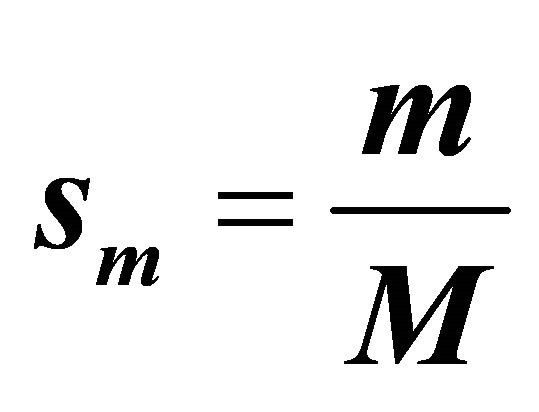 .
.
are in binary form. The binary phase information will be extracted by some number of iterations by IPEA. The extracted phase information should be converted to the corresponding decimal value. And then the obtained decimal value of the relative phase should be substituted into Equation (4) in order to obtain the ground state energy. The decimal value of the relative phase  should be between 0 and 1 and we choose
should be between 0 and 1 and we choose  for simplicity.
for simplicity.
4. Results and Discussion
In this study we concern with obtaining ground state energy by IPEA and simulating the ground state by ASP. Extracting the ground state energy information by a phase estimation algorithm has three main steps: 1) preparing the ground state wave function into qubits by an appropriate mapping, 2) processing controlled operations to extract information and 3) a measurement to readout the extracted information. By evaluating the integrals given in Equation (7), we have the following Hamiltonian matrix which is written in terms of Pauli operators as [27]
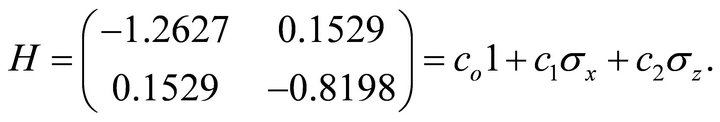 (10)
(10)
Here 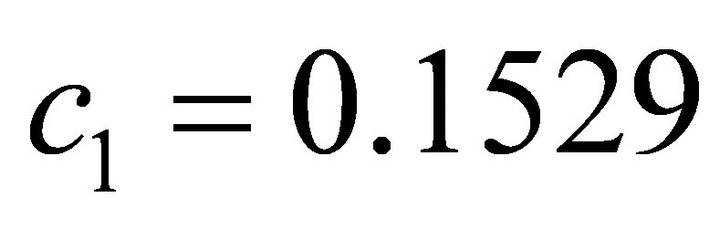 and
and . The theoretical ground state energy is −1.310 356 879 322 492. This value is obtained by diagonalisation of the Hamiltonian matrix. The circuit representation of the two qubit IPEA for calculating ground state energy of 2p-πelectrons in ethylene is shown in Figure 3.The numerical simulation of the proposed implementation is performed by Matlab program.
. The theoretical ground state energy is −1.310 356 879 322 492. This value is obtained by diagonalisation of the Hamiltonian matrix. The circuit representation of the two qubit IPEA for calculating ground state energy of 2p-πelectrons in ethylene is shown in Figure 3.The numerical simulation of the proposed implementation is performed by Matlab program.
The Hamiltonian of the two qubit liquid state NMR quantum register is
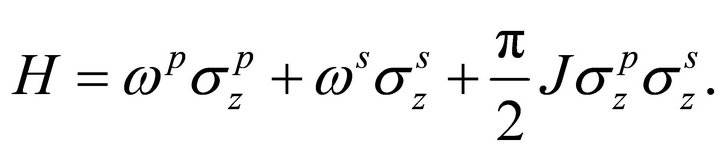 (11)
(11)
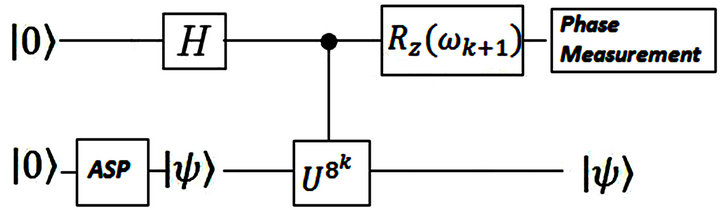
Figure 3. The general scheme of calculating ground state energy of molecular 2p-π electrons in ethylene by a two qubit IPEA.
Where 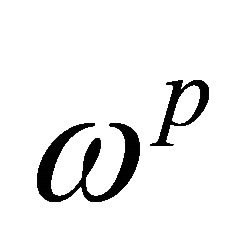 and
and 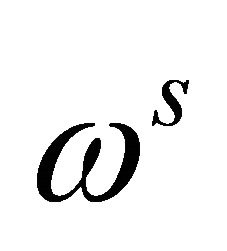 are angular frequencies for the nuclei of the probe and the system qubits, respectively. The scalar coupling
are angular frequencies for the nuclei of the probe and the system qubits, respectively. The scalar coupling , is chosen as
, is chosen as 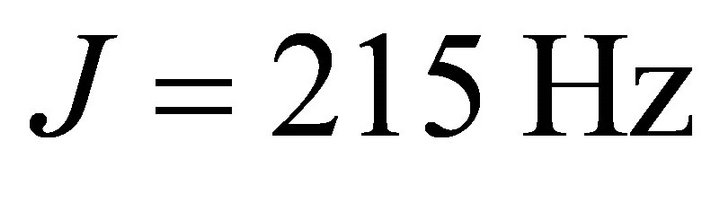 which matches with the value for the Heteronuclear chloroform molecule[28]. The experiment starts with an initial deviation density matrix
which matches with the value for the Heteronuclear chloroform molecule[28]. The experiment starts with an initial deviation density matrix 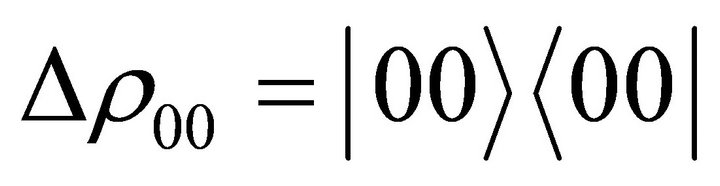 which is a pseudo pure state [29]. A
which is a pseudo pure state [29]. A 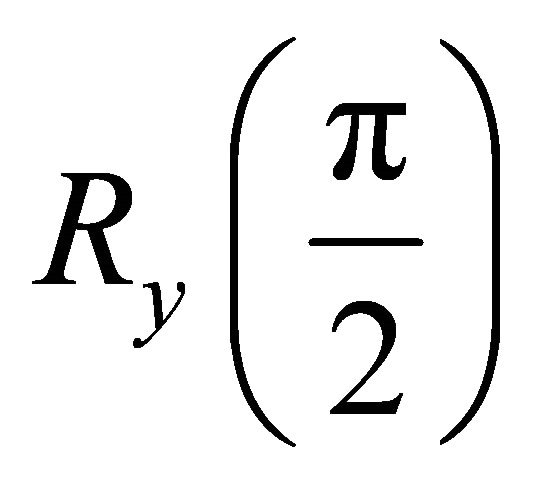 rotation is applied by a pseudo Hadamard gate. And a conjugated
rotation is applied by a pseudo Hadamard gate. And a conjugated 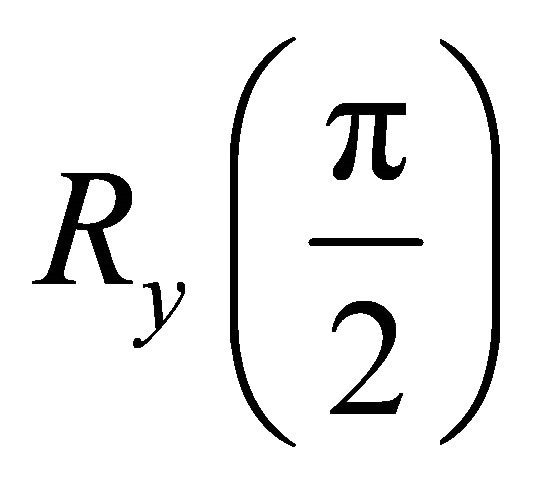 rotation applied to the system qubit to start the ASP process. Thus, the initial Hamiltonian is
rotation applied to the system qubit to start the ASP process. Thus, the initial Hamiltonian is 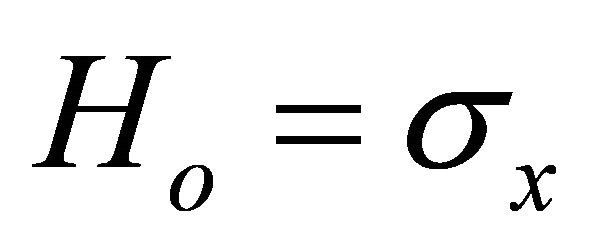 and the problem Hamiltonian is
and the problem Hamiltonian is 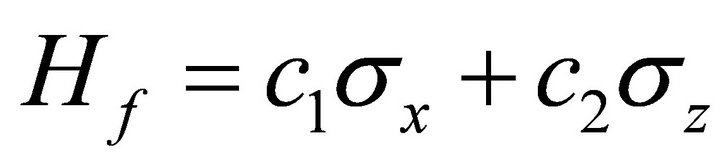 by omitting
by omitting 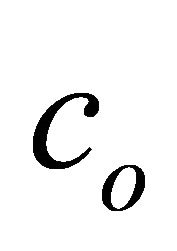 𝟙. The implementation of ASP is carried out by an operator [30]:
𝟙. The implementation of ASP is carried out by an operator [30]:
 (12)
(12)
Here, 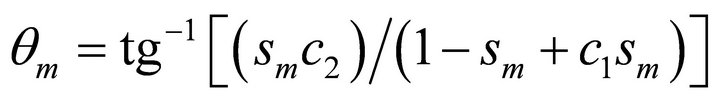 and
and
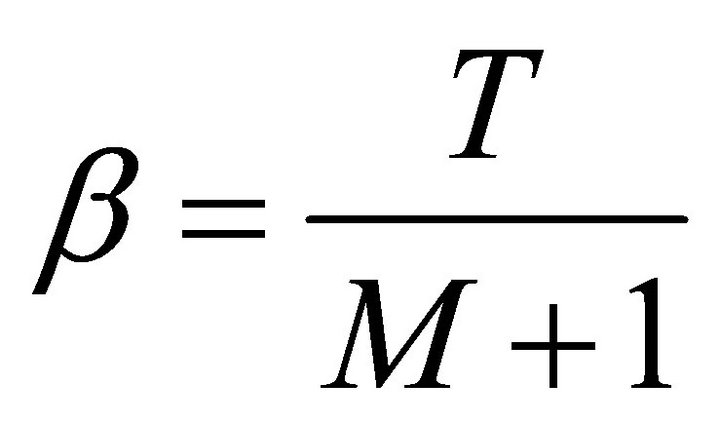 .The overall time
.The overall time 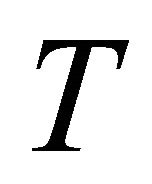 of the adiabatic process has its optimum value of 5 a.u. as indicated in Figure 4. In our demonstration, extracted information is three bits per iteration. Iteration is progressed from more significant bits to less significant ones, implying that iterations starts at
of the adiabatic process has its optimum value of 5 a.u. as indicated in Figure 4. In our demonstration, extracted information is three bits per iteration. Iteration is progressed from more significant bits to less significant ones, implying that iterations starts at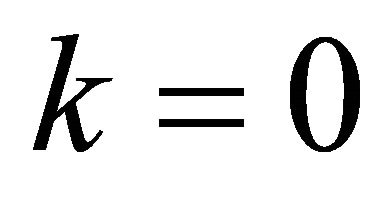 . Thus
. Thus 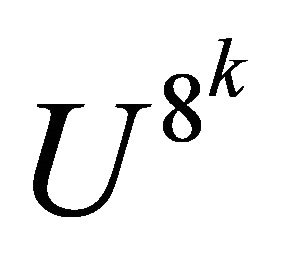 is applied as controlled operation. NMR pulse sequence of the controlled operator is constructed in the operator form as [31]
is applied as controlled operation. NMR pulse sequence of the controlled operator is constructed in the operator form as [31]
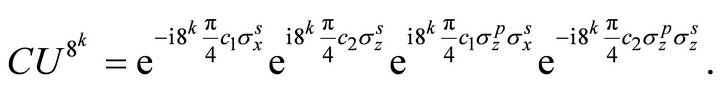 (13)
(13)
In order to apply the gate as an NMR pulse sequence the third operator in the sequence can be written as [31]
 (14)
(14)
The last step of the algorithm is the measurement of the phases. The phase shifts between two states can be read by a phase sensitive NMR spectrum. This readout scheme is referred as an NMR interferometer in which the bit information can be directly extracted from the relative phase measurements of the NMR spectrum [32]. The relative phase shifts (in degrees) after some powers of controlled operations and the extracted binary bits after some iterations are shown in Figure 5. Iterations are formulated as
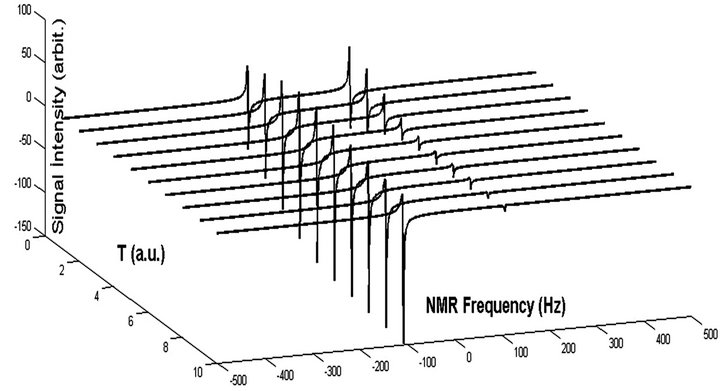
Figure 4. Simulated spectra of the probe qubit after CU operation with respect to different T. T = 5 a.u. is chosen for optimum T.

Figure 5. (a)-(c) Relative Phases after the CU and some powers of CU; (d) The NMR spectrum of pseudo pure state which is fixed as the reference phase for all phase measurements; (e)-(f) First three iterations and the extracted bits.
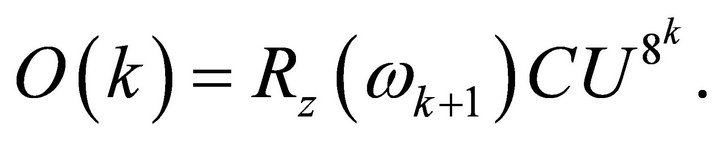 (15)
(15)
Where 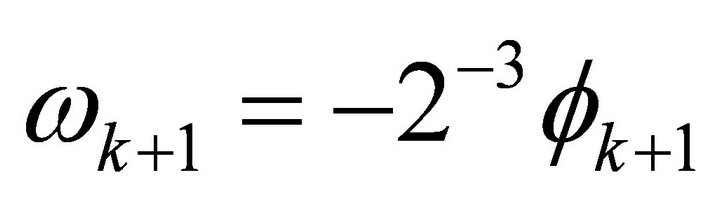 and
and  is the relative phase solely obtained from the powers of controlled operations. The relative phase obtained from the operations, which carry extracted bit information is depicted as
is the relative phase solely obtained from the powers of controlled operations. The relative phase obtained from the operations, which carry extracted bit information is depicted as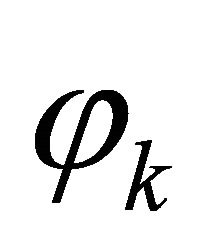 . We choose
. We choose 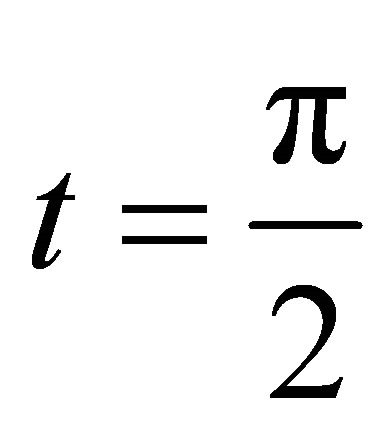 to make
to make 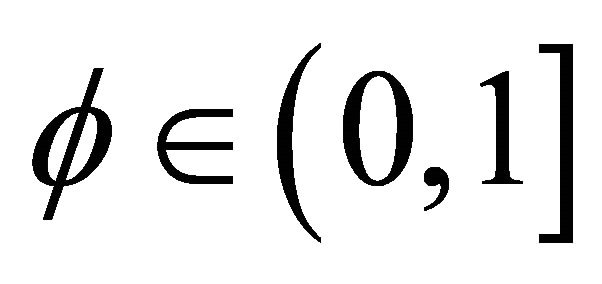 Extracted binary bits were evaluated by Equation (15) and depicted as in Table 1. For instance, in the first iteration for
Extracted binary bits were evaluated by Equation (15) and depicted as in Table 1. For instance, in the first iteration for  the controlled operation is
the controlled operation is  and after this operation obtained relative phase
and after this operation obtained relative phase  is 120 in degrees. And for
is 120 in degrees. And for 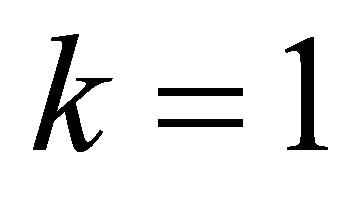 we applied the controlled operation is
we applied the controlled operation is 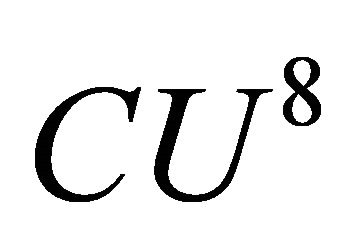 and we had
and we had 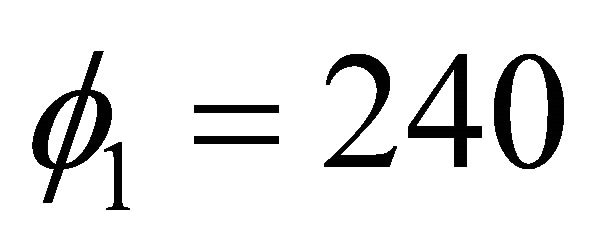 in degrees as shown in Figure 5. The first extracted bits for the first iteration were obtained via Equation (15) such that
in degrees as shown in Figure 5. The first extracted bits for the first iteration were obtained via Equation (15) such that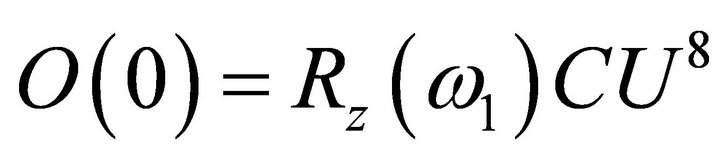 , where
, where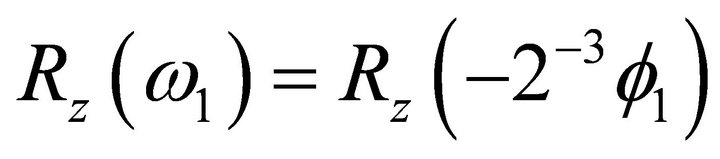 . Concisely the corresponding relative phase for the first iteration is
. Concisely the corresponding relative phase for the first iteration is  in degrees. Corresponding phase factor
in degrees. Corresponding phase factor  can be obtained easily
can be obtained easily
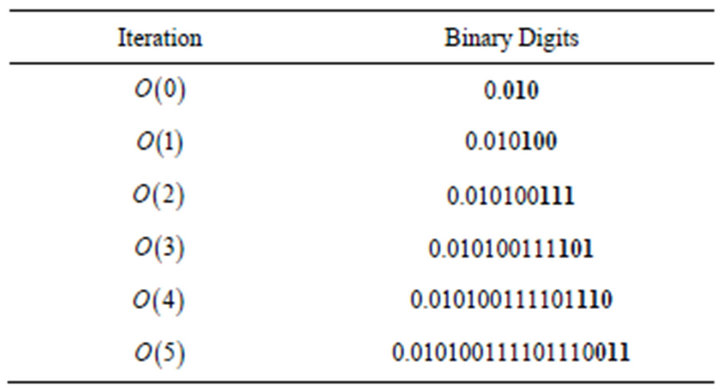
Table 1. Extracted binary bits per iteration. 3 bits extracted per iteration and after 6 iterations 18 binary bits were extracted via relative phases.
by  such that
such that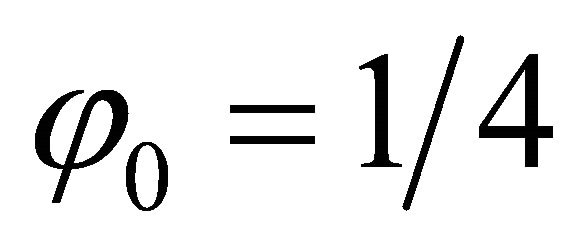 which corresponds to 010 in binary digits. Likewise in the second iteration
which corresponds to 010 in binary digits. Likewise in the second iteration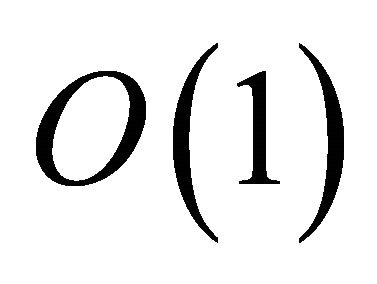 , the extracted bits are 100 and so on.
, the extracted bits are 100 and so on.
After evaluating the extracted binary digits in decimal form, the ground state energy can be obtained from Equation (4). For instance after six iterations, the extracted phase is 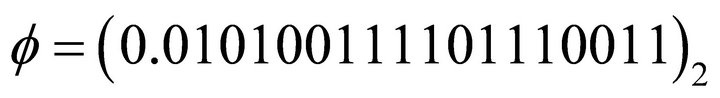 which corresponds to
which corresponds to  in decimal. By substituting this result into Equation (4) one obtains the energy value
in decimal. By substituting this result into Equation (4) one obtains the energy value . This value has four bit accuracy with the theoretically calculated ground state energy. One can improve the energy value by going further iterations. But in a real experimental implementation, the accuracy of the simulation is limited by the experimental errors [33].
. This value has four bit accuracy with the theoretically calculated ground state energy. One can improve the energy value by going further iterations. But in a real experimental implementation, the accuracy of the simulation is limited by the experimental errors [33].
5. Conclusions
In this study, a quantum simulation algorithm is performed to calculate the ground state energy for 2p-π electrons of molecular planar ethylene with a classically simulated two-qubit NMR quantum register. The Hamiltonian of 2p-π electrons in ethylene is written in matrix form and the ground state and the doubly excited state configurations are mapped in the computational basis. A two qubit liquid state NMR Hamiltonian is proposed to perform the implementation as system Hamiltonian for classical simulation. A slightly modified IPEA algorithm is used for the simulation. Adiabatic state preparation is used to prepare system qubit as the ground state of the Hamiltonian in question. By the algorithm three bits are extracted per iteration and the extracted information is progressed from more significant bits to less significant bits. The corresponding decimal value of the phase which is obtained by the extracted bits, yields the energy information from Equation (2). The measurement of the probe qubit is performed by classically simulated phase sensitive NMR spectrum. The pseudo pure state of NMR spectrum is fixed as the reference spectrum throughout the experiment. Hence the quantum simulation of the ground state of 2p-π electrons in ethylene molecule is achieved by a two-qubit NMR quantum register. Also the robustness of the method is examined by comparing obtained ground state energy with the theoretical ground state energy.
REFERENCES
- M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, Cambridge, 2000.
- P. D. Jonathan and J. M. Gerard, “Quantum Technology: The Second Quantum Revolution,” Philosophical Transactions of the Royal Society A, Vol. 361, 2011, pp. 1655- 1674.
- R. P. Feynman, “Simulating Physics with Computers,” International Journal of Theoretical Physics, Vol. 21, No. 6-7, 1982, pp. 467-488. doi:10.1007/BF02650179
- D. Deutsch, “Quantum Theory the Church Turing Principle and Universal Quantum Computer,” Proceedings of the Royal Society A, Vol. 400, No. 1818, 1985, pp. 97- 117.
- P. W. Shor, “Polynomial Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer,” SIAM Review, Vol. 41, No. 2, 1999, pp. 303-332. doi:10.1137/S0036144598347011
- L. K. Grover, “Quantum Mechanics Helps in Searching a Needle in a Haystack,” Physical Review Letters, Vol. 79, No. 2, 1997, pp. 325-328. doi:10.1103/PhysRevLett.79.325
- S. Lloyd, “Universal Quantum Simulators,” Science, Vol. 273, No. 5278, 1996, pp. 1073-1078. doi:10.1126/science.273.5278.1073
- K. L. Brown, W. J. Munro and V. M. Kendon, “Using Quantum Computers for Quantum Simulation,” Entropy, Vol. 12, No. 11, 2010, pp. 2268-2307. doi:10.3390/e12112268
- S. Somaroo, T. F. Havel, R. Laflamme, et al., “Quantum Simulations on a Quantum Computer,” Physical Review Letters, Vol. 82, No. 26, 1999, pp. 5381-5384. doi:10.1103/PhysRevLett.82.5381
- S. Somaroo, T. F. Havel, R. Laflamme, et al., “Quantum Simulation of a Three Body Interaction Hamiltonian on an NMR Quantum Computer,” Physical Review A, Vol. 61, No.1, 1999, Article ID: 012302. doi:10.1103/PhysRevA.61.012302
- A. K. Krithin and B. M. Fung, “NMR Simulation of an Eight State Quantum System,” Physical Review A, Vol. 64, No. 3, 2001, Article ID: 032306. doi:10.1103/PhysRevA.64.032306
- G. Ortiz, E. Knill, R. Laflamme, et al., “Liquid State NMR Simulations of Quantum Many Body Problems,” Physical Review A, Vol. 71, No. 3, 2005, Article ID: 032 344. doi:10.1103/PhysRevA.71.032344
- X. Peng , J. Du and D. Suter, “Quantum Phase Transition of Ground State Entanglement in a Heisenberg Spin Chain Simulated in an NMR Quantum Computer,” Physical Review A, Vol. 71, No. 1, 2005, Article ID: 012307. doi:10.1103/PhysRevA.71.012307
- D. S. Abrams and S. Lloyd, “Quantum Algorithm Providing Exponantial Speed Increase for Finding Eigenvalues and Eigenvectors,” Physical Review Letters, Vol. 83, No. 24, 1999, pp. 5162-5165. doi:10.1103/PhysRevLett.83.5162
- R. Cleve, A. Ekert, M. Mosca, et al., “Quantum Algorithms Revisited,” Proceedings of the Royal Society of London A, Vol. 454, No. 1969, 1998, pp. 339-354.
- A. A. Guzik, A. D. Dutoi, P. J. Love, et al., “Simulated Quantum Computation of Molecular Energies,” Science, Vol. 309, No. 5741, 2005, pp. 1704-1707. doi:10.1126/science.1113479
- A. Messiah, “Quantum Mechanics,” Wiley, New York, 1976.
- I. Kassal, M. Mohseni, A. A. Guzik, et al., “PolynomialTime Quantum Algorithm for the Simulation of Chemical Dynamics,” PNAS, Vol. 105, No. 48, 2008, pp. 18681- 18686. doi:10.1073/pnas.0808245105
- I. Kassal, A. P. Ortiz, A. A. Guzik, et al., “Simulating Chemistry Using Quantum Computers,” Annual Review of Physical Chemistry, Vol. 62, No. 1, 2011, pp. 185-207. doi:10.1146/annurev-physchem-032210-103512
- B. P. Lanyon, I. Kassal, A. A. Guzik, et al., “Towards Quantum Chemistry on a Quantum Computer,” Nature Chemistry, Vol. 2, No. 2, 2010, pp. 106-111. doi:10.1038/nchem.483
- J. Du, X. Peng, D. Lu, et al., “NMR Implementation of a Molecular Hydrogen Simulation with Adiabatic State Preparation,” Physical Review Letters, Vol. 104, No. 3, 2010, Article ID: 030520. doi:10.1103/PhysRevLett.104.030502
- J. D. Whitfield, J. Biamonte and A. A. Guzik, “Simulation of Electronic Structure Hamiltonians Using Quantum Computers,” Molecular Physics, Vol. 109, No. 5, 2011, pp. 735-750. doi:10.1080/00268976.2011.552441
- Z. Li , X. Peng, A. A. Guzik, et al., “Solving Ground State Problems with Nuclear Magnetic Resonance,” Scientific Reports, Vol. 1, No. 88, 2011, pp. 1-7.
- M. Dobsicek, G. Johansson, G. Wendin, et al., “Arbitrary Accuracy Iterative Quantum Phase Estimation Algorithm Using a Single Ancillary Qubit: A Two-Qubit Benchmark,” Physical Review A, Vol. 76, No. 3, 2007, Article ID: 030306. doi:10.1103/PhysRevA.76.030306
- M. Steffen, W. V. Dam, I. Chuang, et al., “Experimental Implementation of an Adiabatic Optimization Algorithm,” Physical Review Letters, Vol. 90, No. 6, 2003, Article ID: 067903. doi:10.1103/PhysRevLett.90.067903
- A. Szabo and N. S. Ostlund, “Modern Quantum Chemistry,” Dover Publications Inc., New York, 1996.
- R. G. Parr, “The Quantum Theory Molecular Electronic Structure,” W.A. Benjamin Inc., New York, 1963.
- R. Laflamme, D. G. Cory, T. F. Havel, et al., “NMR and Quantum Information Processing,” Los Alamos Science, Vol. 27, 2002, pp. 227-259.
- J. A. Jones, “Quantum Computing with NMR,” Progress in Nuclear Magnetic Resonance Spectroscopy, Vol. 59, No. 2, 2011, pp. 91-120. doi:10.1016/j.pnmrs.2010.11.001
- M. H. Levitt, “Spin Dynamics,” John Wiley & Sons, Chichester, 2001.
- M. D. Price, S. S. Somaroo, T. F. Havel, et al., “Construction and Implementation of NMR Quantum Logic Gates for Two Spin Systems,” Journal of Magnetic Resonance,Vol. 140, No. 2, 1999, pp. 371-378.
- X. Peng, D. Suter, K. Gao, et al., “Quantification of Complementarity in Multiqubitsystems,” Physical Review A, Vol. 72, No. 5, 2005, Article ID: 052109. doi:10.1103/PhysRevA.72.052109
- K. R. Brown, R. J. Clark and I. L. Chuang, “Limitations of Quantum Simulation Examined by Simulating a Pairing Hamiltonian Using Nuclear Magnetic Resonance,” Physical Review Letters, Vol. 97, No. 5, 2006, Article ID: 050504. doi:10.1103/PhysRevLett.97.050504
NOTES
*Corresponding author.

