Journal of Quantum Information Science
Vol.3 No.4(2013), Article ID:40160,5 pages DOI:10.4236/jqis.2013.34018
Quantum Walk of Two Quantum Particles on One Dimensional System
Department of Applied Physics, Nanjing University of Aeronautics and Astronautics, Nanjing, China
Email: *zymzym@nuaa.edu.cn
Copyright © 2013 Yongmei Zhang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 30, 2013; revised October 19, 2013; accepted November 12, 2013
Keywords: Quantum Walk; Hadamard Operation; Probability Distribution; Correlation Probability
ABSTRACT
We study two particle quantum walks on one dimensional chain. Probability distribution of two particle quantum walks is dependent on the initial state, and symmetric quantum walk or asymmetric quantum walk is analogous to that of one particle quantum walk. The quantum correlation probability is much different from classical coincidence probability. The difference reflects quantum interference between two particles.
1. Introduction
Random walk is relevant to many aspects of our lives, providing insight into diverse fields. It forms the basis of algorithms [1] and describes diffusion processes in physics or biology, such as Brownian motion [2]. It has also been used as a model for stock market prices [3]. Quantum walk is the quantum counterpart of classical random walk. It is immediately noticed that quantum walks behave quite differently from classical random walk [4]. Quantum walk is expected to have implications for various fields, for instance, as a primitive for universal quantum computing [5], systematic quantum algorithm engineering [6], or for deepening our understanding of the efficient energy transfer in biomolecules for photosynthesis [7]. Quantum walk has attracted a great deal of attention in the scientific community in recent years. There have been several suggestions for practical implements of quantum random walks, such as trapped ions [8, 9], optical lattices [10,11] and QED cavity[12].
In this paper, we aim to numerically simulate quantum walks of one or two quantum particles on a chain. The quantum correlation probability is much different from classical coincidence probability. The difference reflects quantum interference between two particles. Quantum interference is matter wave interference based on waveparticle dualism of quantum mechanics.
The paper is organized as following. In Section 2, the quantum walk operations are introduced. In Section 3, distribution probability of two particles is displayed. The comparison between two particle quantum walks with one particle quantum walk is stated in Section 4. Brief conclusions are given in Section 5.
2. Quantum Walk in One-Dimensional Systems
Quantum walk on a line is a simple example which shows many properties of quantum walks. It is often used as a tool in the analysis of quantum walks on more complicated graphs [4].
In a classical random walk on the line, a particle is in a certain location at start. At each time step, the particle moves left or right randomly with probability 1/2. This is realized by throwing a coin. If the coin is upward, the particle moves left. Otherwise the particle moves right. After many time steps, the random walk yields a binomial probability distribution.
Quantum walk is realized on a line or a circle by a quantum coin. Let Hp be the Hilbert space spanned by the positions of the particle. The basis states of the space are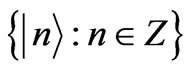 , where
, where  corresponds to a particle localized in position
corresponds to a particle localized in position . However, quantum walker has been assigned an additional quantum degree of freedom which could be spin or other chirality [13]. The walker goes left or right depending on the spin degree of freedom. Thus the position space is augmented by coin space HX spanned by two basis states
. However, quantum walker has been assigned an additional quantum degree of freedom which could be spin or other chirality [13]. The walker goes left or right depending on the spin degree of freedom. Thus the position space is augmented by coin space HX spanned by two basis states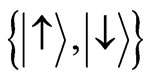 . States of the total system are in the space of
. States of the total system are in the space of  [14].
[14].
Suppose the particle is initially localized on site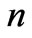 . The initial state of the particle is
. The initial state of the particle is
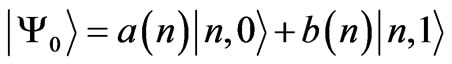 (1)
(1)
where  are complex amplitudes of the state. According to normalization, we have
are complex amplitudes of the state. According to normalization, we have
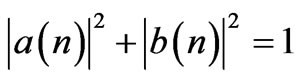 . If the initial state is asymmetricthen
. If the initial state is asymmetricthen  and
and . The symmetric state corresponds to
. The symmetric state corresponds to  and
and
 [15]. In each time step, there are two operations, coin flip operation and shift operation. The coin flip operation generates a superposition state
[15]. In each time step, there are two operations, coin flip operation and shift operation. The coin flip operation generates a superposition state
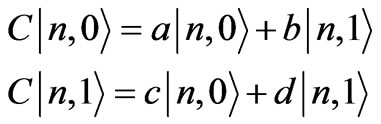 (2)
(2)
A frequently used balanced unitary coin is the so called Hadamard coin H
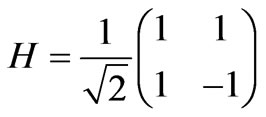 .
.
In the shift operation, spin-up state moves left while spin-down state moves right.
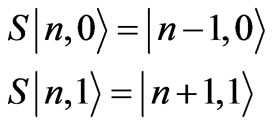 (3)
(3)
Running N time steps of quantum walk, the probability distribution is very different from the classical normal distribution.
What is quantum walk mechanics of two particles on a chain? Suppose initially one particle is on site 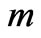 and the other on site
and the other on site . Since each particle has spin states, the initial state of the system is expressed as following.
. Since each particle has spin states, the initial state of the system is expressed as following.
 (4)
(4)
where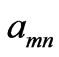 ,
,  ,
, 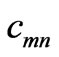 and
and 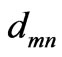 are complex amplitudes of the state. Because of normalization,
are complex amplitudes of the state. Because of normalization,
 .
.
The quantum coin in two particle case is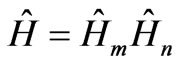 . where
. where 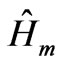 is quantum flip operation on the
is quantum flip operation on the 
particle and  is quantum flip on the
is quantum flip on the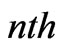 . Thus the Hadamard coin is
. Thus the Hadamard coin is
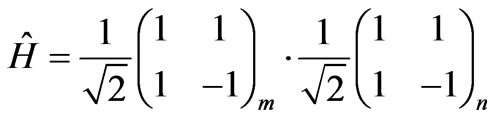 (5)
(5)
First, the Hadamard coin operates on the initial state. The coin flip operation generates new superposition state.
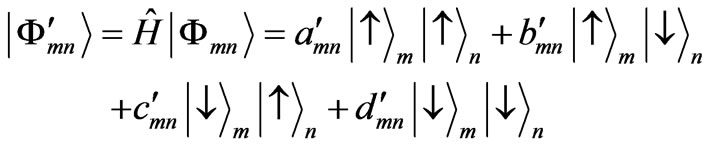 (6)
(6)
In which
 (7)
(7)
Second, the particle states moves along the chain according to their spin states. Spin-up state moves left while spin-down state moves right. We have the following recursion relations.
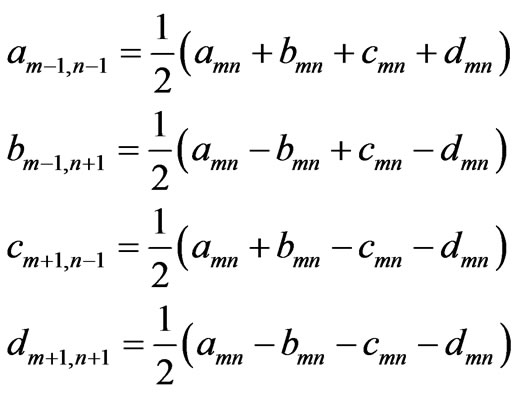 (8)
(8)
One step of quantum walk is accomplished in this way.
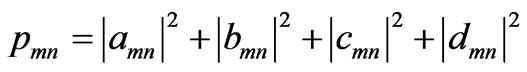 is called correlation probability. That is probability of one particle on site
is called correlation probability. That is probability of one particle on site  and the other on site
and the other on site 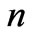 after
after 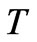 steps quantum walk. If
steps quantum walk. If 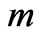 and
and 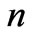 are same, that is probability of two particles coincide on one site.
are same, that is probability of two particles coincide on one site.
3. Quantum Walk Probability Distribution of Different Initial States
Suppose two particles are indistinguishable. There are three types of initial spin conditions: both spin up, both spin down, one spin up and the other spin down. The initial states are

We simulate ten step quantum walk on a chain of length 21 and calculate the correlation probability. Figure 1 and Figure 2 both correspond to the first initial state in which two spin up particles locate on two different sites in the middle of the chain. After 10 steps of quantum walks, maximum probability appears on site 4 and 6. It reflects that spin up particles move left with bigger probability. Similar result happens to the third initial state. But the moving direction of spin down particles is right.
The correlation probability after ten steps quantum walk with initial state of one spin up and the other spin down is displayed in Figures 3 and 4. The maximum correlation probability is at (18,4) or (4,18). This indicates big probability of one particle moves to site 4
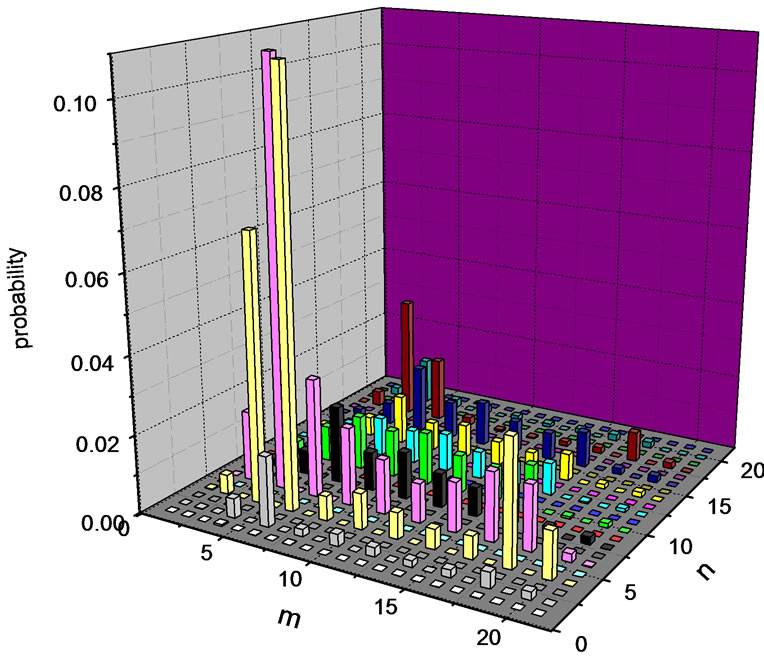
Figure 1. Correlation probability of two particles quantum walk on a chain of length 21 after 10 steps. Two spin up particles initially locate on site 10 and 12 respectively. The two particles mainly move left on the chain.
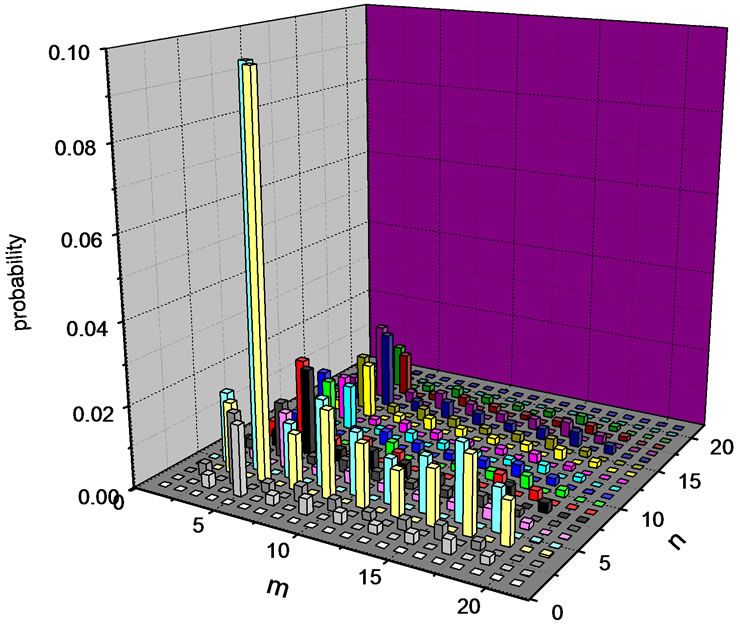
Figure 2. Correlation probability of two particles quantum walk on a chain of length 21 after 10 steps. Two spin up particles initially locate on site 10 and 11 separately. The two particles mainly move left on the chain. The probability is more concentrated in this case.
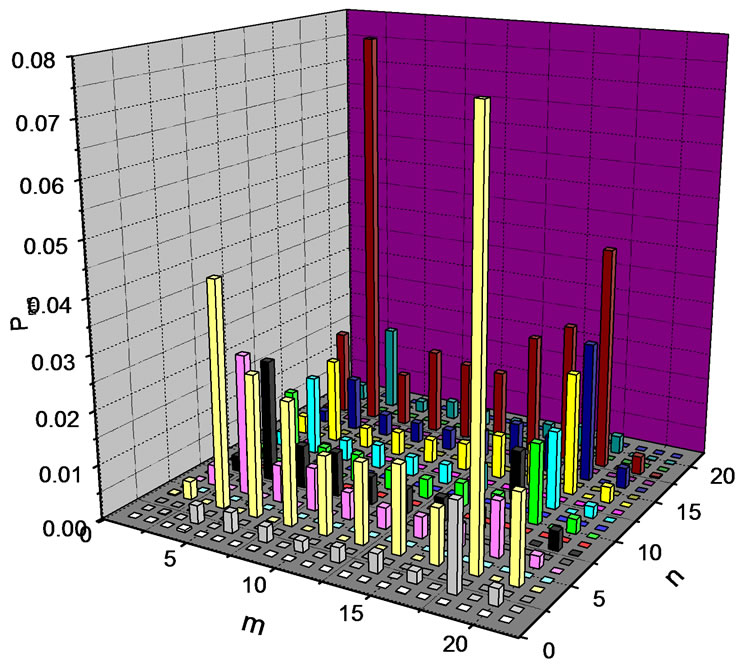
Figure 3. Correlation probability after 10 steps of quantum walk on a chain with 21 site. The two particles are initially at site 10 with spin up and site 12 with spin down. The probability of moving to opposite directions is big. The probability of returning to the starting point is small. But there is certain probability that they move to the same direction.
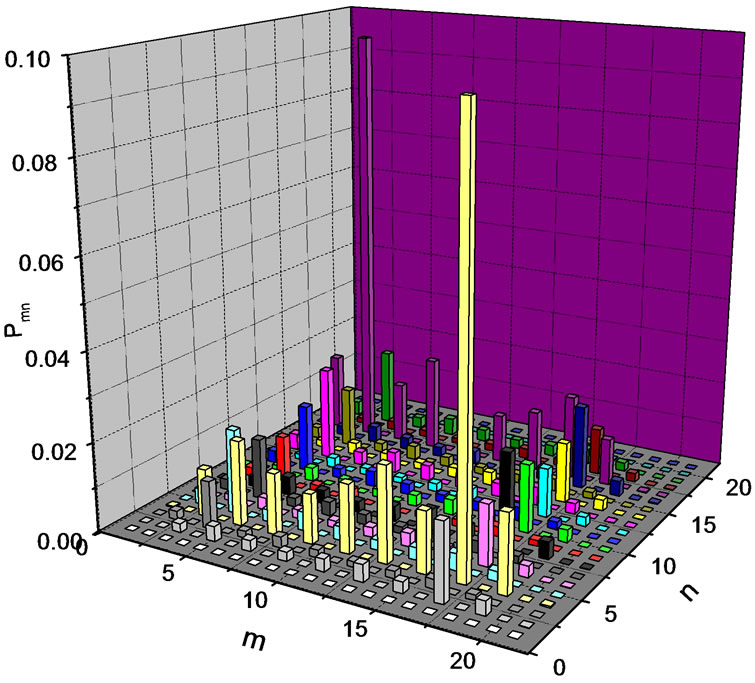
Figure 4. Correlation probability after 10 steps of quantum walk on a chain with 21 site. The two particles are initially at site 10 with spin up and site 11 with spin down. The probability of moving to opposite directions is big, but the probability of moving to the same direction is small. The probability of returning to the starting point is small, too.
and the other moves to site 18. But the probability of returning to their original locations is small. This result is consistent with the outcome of waveguide array experiment in ref. [16]. In ref.[16], correlated photons are coupled into central waveguides of the array. After a period of time, the output light tense is big at the two lobes. Photons undergoes quantum walk in the waveguide and goes out far from the center. However, there is some difference between Figures 3 and 4. The correlation probabilities at (4,4) and (18,18) are bigger in Figure 3 than that in Figure 4. If the two particles are initially one site interval, each of them move right or left and overlap on some sites. When two particles are initially located nearby, they often stagger each other. There is little chance to reinforce.
4. Comparison with One Particle Quantum Walk
Two particle quantum walk on a long chain is also studied. The results are displayed in Figures 5 and 6. Suppose the two particles are at site 200 and 201 at beginning. When they both spin up, they tends to move left after some steps. If one is spin up and one spin is down, the probability distribution is symmetrical. These
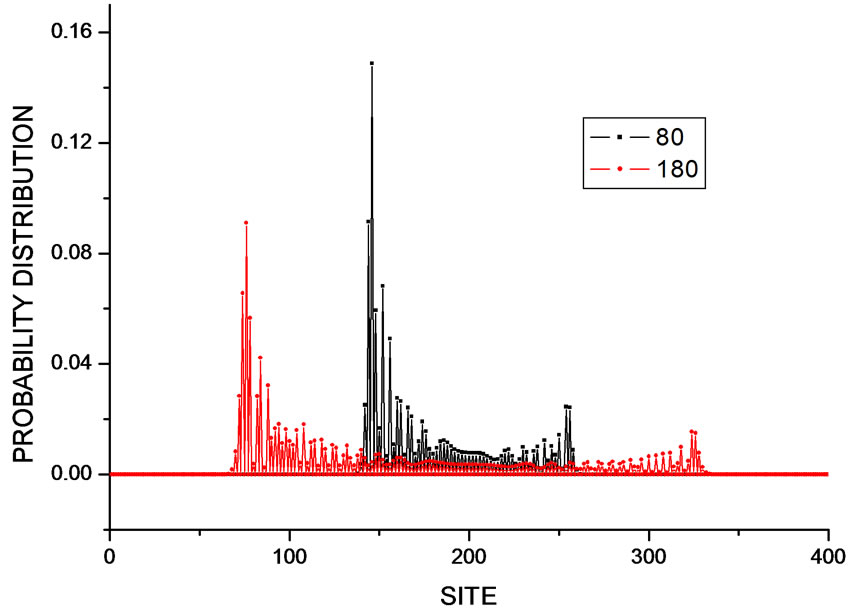
Figure 5. Probability distribution of two particle quantum walk on a chain of N = 400. Two spin up particles are initially at site 200 and 201.Time steps are 80 and 180 respectively. The particles move to the left. The result is similar to one particle quantum walk.
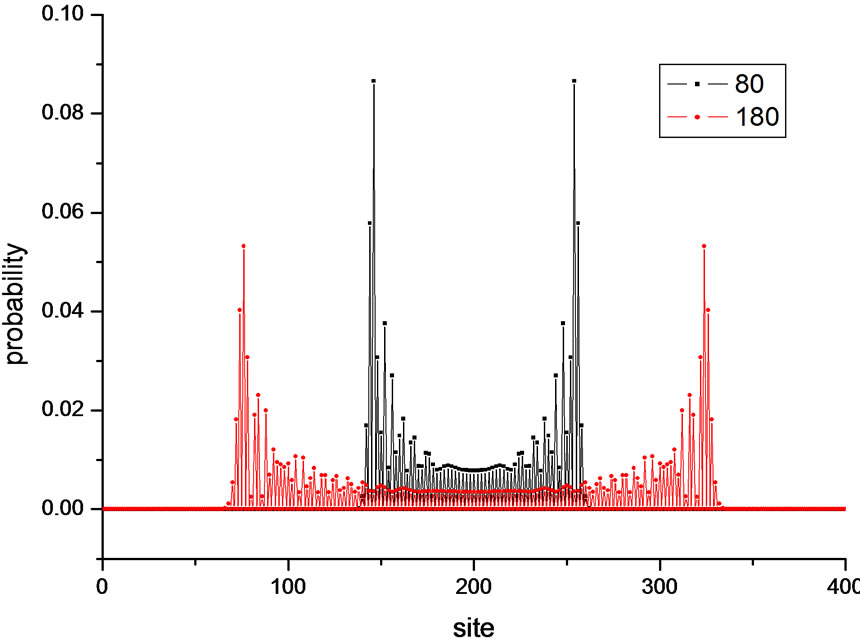
Figure 6. Probability distribution of two particle quantum walk on a chain of N = 400. One is spin up while the other is spin down initially at site 200 and 201. Time steps are 80 and 180 respectively. The quantum walk is symmetric. It is similar to one particle quantum walk.
results are similar to one particle quantum walk on a chain [14].
In classical statistics, the coincidence probability of two events is equal to the multiply of probabilities of single events. That is  [17]. In quantum random walks, one particle at site
[17]. In quantum random walks, one particle at site  is treated as an event. The probability of this event is
is treated as an event. The probability of this event is . The probability of the other particle on site
. The probability of the other particle on site 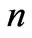 is
is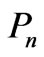 . The probability of one particle at site
. The probability of one particle at site 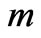 and the other particle at site
and the other particle at site  is
is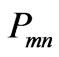 . In this work of two particle quantum walk, it is found that correlation probability is not equal to multiply of single event probabilities. Figure 7 is the difference between
. In this work of two particle quantum walk, it is found that correlation probability is not equal to multiply of single event probabilities. Figure 7 is the difference between  and
and 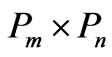 where
where 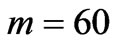 and
and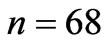 . There is no difference in the first 20 steps because the particles have not arrives at site 60 or 68. When the particles arrive at the specific sites, quantum correlation probability is bigger than coincidence probability. During 20 and 50 steps, the difference changes severely. After 50 steps, the difference is very small because the particles have passed the objective sites. This manifests that correlation probability is distinct with coincidence probability in quantum random walk.
. There is no difference in the first 20 steps because the particles have not arrives at site 60 or 68. When the particles arrive at the specific sites, quantum correlation probability is bigger than coincidence probability. During 20 and 50 steps, the difference changes severely. After 50 steps, the difference is very small because the particles have passed the objective sites. This manifests that correlation probability is distinct with coincidence probability in quantum random walk.
5. Conclusion
We study two particle quantum walks on one dimensional chain. Probability distribution of two particle quantum walks is dependent on the initial state, such as location and spin. The properties of symmetric quantum walk and asymmetric quantum walk are analogous to that of one particle quantum walk. When the two particles are one site apart initially, diffusion is faster and probability distribution is even on the chain. The quantum correlation probability is much different from classical coin-

Figure 7. The difference between quantum correlation probability and multiply of two single probabilities. Two spin up particles are initially on site 80 and 88 on the chain of N = 160.
cidence probability. This difference reflects quantum interference between two particles.
REFERENCES
- M. Barber, “Random and Restricted Walks: Theory and Applications,” Gordon and Breach, New York, 1970.
- H. C. Berg, “Random Walk in Biology,” Princeton, 1993.
- E. F. Fama, Financ. Anal., J, 51, 75(1995). http://dx.doi.org/10.2469/faj.v51.n1.1861
- A. Ambainis, “Quantum Walks and Their Algorithmic Application,” 2004. arXiv: quantu-ph/0403120v3
- A. M. Childs, “Universal Computation by Quantum Walk,” Physical Review Letters, Vol. 102, No. 18, 2009, Article ID: 180501. http://dx.doi.org/10.1103/PhysRevLett.102.180501
- W. Dur, R. Raussendorf, V. M. Kendon and H. Brieget, “Quantum Walks in Optical Lattices,” Physical Review A, Vol. 66, No. 5, 2002, Article ID: 052319. http://dx.doi.org/10.1103/PhysRevA.66.052319
- R. J. Sension, “Biophysics: Quantum Path to Photosynthesis,” Nature, Vol. 446, 2007, pp. 740-741. http://dx.doi.org/10.1038/446740a
- F. Zahringer, et al., “Realization of a Quantum Walk with One and Two Trapped Ions,” Physical Review Letters, Vol. 104, No. 10, 2010, Article ID: 100503. http://dx.doi.org/10.1103/PhysRevLett.104.100503
- P. Xue, B. C. Sanders and D. Leibfried, “Quantum Walk on a Line for a Trapped Ion,” Physical Review Letters, Vol. 103, No. 18, 2009, Article ID: 183602. http://dx.doi.org/10.1103/PhysRevLett.103.183602
- H. B. Perets, Y. Lahini, F. Pozzi, et al., “Realization of Quantum Walks with Negligible Decoherence in Waveguide Lattices,” Physical Review Letters, Vol. 100, No. 17, 2008, Article ID: 170506. http://dx.doi.org/10.1103/PhysRevLett.100.170506
- H. S. Eisenberg, Y. Silberberg, R. Morandotti, et al., “Discrete Spatial Optical Solitons in Waveguide Arrays,” Physical Review Letters, Vol. 81, No. 16, 1998, pp. 3383- 3386. http://dx.doi.org/10.1103/PhysRevLett.81.3383
- R. Rangel, N. Zagury and E. Massoni, “Dynamics of a Single Trapped Ion inside a Nonideal QED Cavity at Zero Temperature,” Physical Review A, Vol. 69, No. 2, 2004, Article ID: 023805. http://dx.doi.org/10.1103/PhysRevA.69.023805
- P. K. Pathak and G. S. Agarwal, “Quantum Random Walk of Two Photons in Separable and Entangled State,” 2006. arXiv: quant-ph/0604138v3
- J. Kempe, “Quantum Random Walks: An Introductory Overview,” 2003. arXiv: quant-ph/0303081v1
- X. P. Xu, “Discrete-Time Quantum Walks on One-Dimensional Lattices,” The European Physical Journal B, Vol. 77, No. 4, 2010, pp. 479-488. http://dx.doi.org/10.1140/epjb/e2010-00267-2
- A. Peruzzo, M. Lobino, J. C. F. Matthews, et al., “Quantum Walks of Correlated Photons,” Science, Vol. 329, No. 5998, 2010, pp. 1500-1503. http://dx.doi.org/10.1126/science.1193515
- Y. Bromberg, Y. Lahini, R. Morandotti, et al., “Quantum and Classical Correlations in Waveguide Lattices,” Physical Review Letters, Vol. 102, No. 25, 2009, Article ID: 253904. http://dx.doi.org/10.1103/PhysRevLett.102.253904
NOTES
*Corresponding author.

