ABSTRACT

Steganography is a technique hiding secret information within innocent-looking information (e.g., text, audio, image, video, and so on). In this paper, we propose a quantum steganography protocol using plain text as innocent-looking information called cover data. Our steganograpy protocol has three features. First, we can use any plain text that is independent of any secret message sent between parties. When we make stego data, we do not need to change the content of plain text at all. Second, embedded messages are not included in opened information (innocent-looking messages), but are included as phases of the entangled states. Finally, in quantum states shared between parties in advance, i.e., as quantum keys used when the parties recover secret messages from stego data, neither innocent-looking information nor the information of any secret message is included.

1. Introduction

Both superposition states and entangled states have been effectively used in many fields of quantum information. For instance, Shor’s quantum algorithms for prime factorization and discrete logarithms are typical examples [1]. However, it is also thought that his results will threaten partial security of information processing (the security of public key cryptosystems) in the future. In this situation, some quantum cryptosystems based on quantum physics have been also proposed [2-4], and have proved to be unconditionally secure [5-9].

As a result of typical quantum information security, Bennett and Brassard proposed a quantum cryptosystem called BB84 [2]. This system effectively uses superposetion states, and exchanges secret information between parties. Moreover, quantum secret sharing is proposed in order to store and manage information securely (e.g., see [10]). The subject of this problem is to share secret information among parties. Under cooperating among the parties, some parties can obtain some useful information. As being derived from the quantum secret sharing, quantum data hiding is also proposed [11-14]. The subject is to construct a protocol such that parties cannot recover secret information using only local operations supplemented by classical communication among them although this protocol also shares information among them.

Recently, quantum steganography has been also studied. Steganography is a technique hiding secret information within innocent-looking information (e.g., text, audio, image, video, and so on). Cryptography is to make information unreadable against any eavesdropper, whereas steganography is to hide information against any eavesdropper. Messages made by cryptography are obviously unnatural, and eavesdroppers can easily regard them as targets. On the other hand, messages made by steganography are natural. Therefore, eavesdroppers may pass them with high probability.

Early results of quantum steganography such as [15,16] (see also [17,18]) using superdense coding and [19] using quantum error-correcting codes are not sufficient because their results showed protocols sending secret information (embedded information, or embedded message) between parties securely, but did not show the technique embedding it within innocent-looking information (cover data). Martin also proposed a notion of quantum steganographic communication [20], i.e., he proposed a quantum channel hidden within a quantum key distribution protocol such as BB84. In this situation, Shaw and Brun constructed a quantum steganography protocol using quantum errorcorrecting codes [21]. Their protocol showed a method embedding secret information (stego data) to cover data.

In this paper, we propose a quantum steganography protocol using plain text as cover data. First, we make a quantum entangled state representing a classical message. This quantum state means the cover data corresponding to the message. Next, we make quantum stego data includeing an embedded message by being included the cover data within the stego data.

The features of our steganograpy protocol are as follows. First, we can use any plain text that is independent of any secret message (i.e., any embedded message). When we make stego data, we do not need to change the contents of innocent-looking messages at all. Namely, any eavesdropper cannot distinguish the cover data from the stego data. On the other hand, in Shaw and Brun’s protocol, the cover data must be modified in order to embed secret messages as error-correcting codes [21]. Therefore, the stego data made by their protocol slightly differs from the original cover data. Second, roughly speaking, embedded messages are not included in opened information (innocent-looking messages) although they are included as partial information of the stego data within the quantum entangled states. They are included as phases of the states, and nobody can know the information except for legitimate parties. Finally, in quantum states shared between the parties in advance, i.e., as quantum keys used when the parties recover secret messages from stego data, only the entangled state of a form of 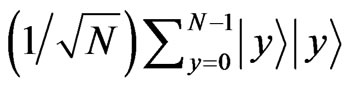is shared between parties. In this quantum state, neither innocent-looking information nor the information of any secret message is included. Thus, any useful information does not leak in this procedure.

The remainder of this paper has the following organization. In Section 2, we show a quantum entangled state used as cover data. Although the form of this state seems to differ from the form of the stego data mentioned in Section 3, we show the relationship between the cover data and the corresponding stego data in Section 4. In Section 3, we construct a quantum steganography protocol. In Section 4, we evaluate secrecy and security of our protocol. Finally, in Section 5, we describe some concluding remarks.

2. Cover Data

We consider a situation such that a party Alice wants to send a classical message 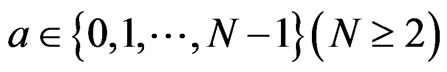to another party Bob. This message may not be secret to anybody, i.e., the information may be stolen by any eavesdropper or Alice may open it intentionally.

In this situation, we construct a protocol in the following way. First, Alice makes a quantum state

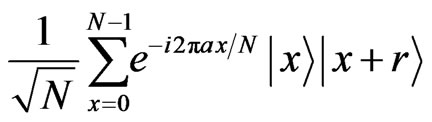
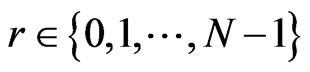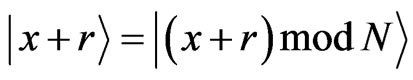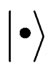corresponding to the classical message a, where is a random number chosen by her. Throughout this paper, the outcome of the addition is congruent modulo N, i.e., , we call each state a register (although is only called a register when for some positive integer n usually), and . Next, she sends the state to Bob. Finally, Bob can recover the message a by applying a quantum Fourier Transform,

to the two registers. Namely, by applying the quantum Fourier Transform, the state becomes

where we use the property such that  if , otherwise the sum is zero if 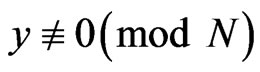 . Then, Bob can recover the message a because he can obtain and  satisfying 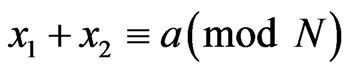by measuring the two registers.

In the next section, we use the form of this state made by Alice as a partial state of stego data, i.e., as cover data.

3. Our Steganography Protocol

In this section, we show a quantum steganography protocol such that Alice sends a classical message to Bob secretly by embedding to the message a mentioned in Section 2.

In general, stego data is constructed by modifying cover data, i.e., stego data is made by embedding a secret message to cover data. However, our stego data in our protocol is constructed by combining some quantum states with a secret message and a classical message corresponding to cover data. Although we showed cover data 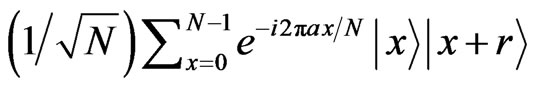corresponding to the message a in Section 2, our stego data is not constructed by embedding a secret message m to the state but includes the quantum state of the cover data finally.

We construct a protocol in the following way.

Our Proposed Protocol

Step 1: Alice and Bob share an entangled state

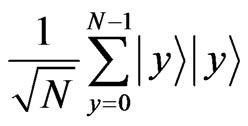
in advance, where Alice has the first register, and Bob has the second one. The state must be shared securely between the parties. Note that this step can be executed between them with being independent of both a secret message m and a cover message a, i.e., they do not need to decide the messages in this step.

Step 2: After deciding a secret message m sending to Bob and a cover message a, Alice makes a state

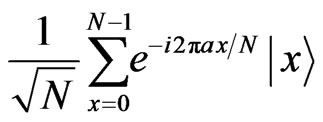
corresponding to the cover message a, and embeds the message m to the state in Step 1 as follows:

Step 3: Alice combines the two states in Step 2, and makes an entangled state from them, i.e., she adds the first register to the second register.

This state is the stego data corresponding to the message m embedded to the message a. Note that the message m is independent of the message a. Therefore, Alice can use any natural plain text as the classical message constructing cover data, and do not need to modify the message in constructing the corresponding stego data.

Step 4: Alice sends her two registers to Bob. The registers may be opened to anybody in public.

Step 5: Bob can recover the secret message m by applying the quantum Fourier transform to all the registers, i.e.,

Then, Bob can recover the message m because he can obtain and 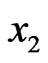satisfying 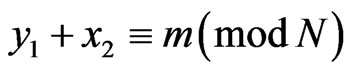by measuring the state (obviously, he can also recover the message a).

4. Secrecy and Security

First, we study a relationship between the stego data and the cover data. The stego data in Step 3 mentioned in the previous section is

On the other hand, the cover data mentioned in Section 2 is

Thus, the state of the cover data is the same form as a part of the stego data,. This means that we can also regard the stego data as the state made by the following way except for Bob’s register. Although the state may not be constructed in order mentioned in the following procedure, we focus on a relationship between the stego data and the cover data.

First, Alice chooses a random number 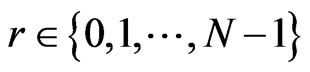 , and makes a state

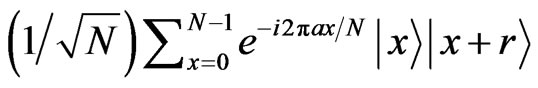corresponding to the message a. Next, the phase corresponding to the secret message m, , is applied, i.e.,

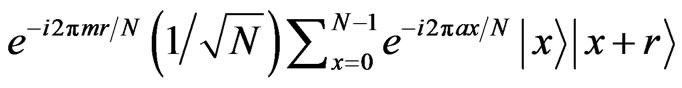. Finally, by computing all the sum from 0 to 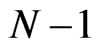of any random number r for the state, the state becomes

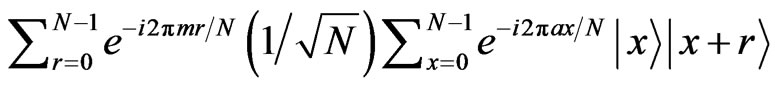. Note that the state is the same state as the stego data except for Bob’s register.

By considering this process, we can conclude that our stego data can be made without changing the cover data. Therefore, the difference between Alice’s registers revealed in Step 4 and the cover data cannot be found. Then, any eavesdropper cannot distinguish the cover data from the stego data even if Alice’s registers in Step 4 is revealed, and the secrecy is held.

Next, Even if somebody applies the quantum Fourier transform to the partial state of the stego data (opened by Alice) and measures the two registers, the message m can be recovered by Bob if he can know the outcome measured by the third party. Here, we observe the situation such that Bob executes his procedure after the cover data opened by Alice is operated and is measured.

First, by applying the quantum Fourier transform, the state of the stego data becomes as follows:

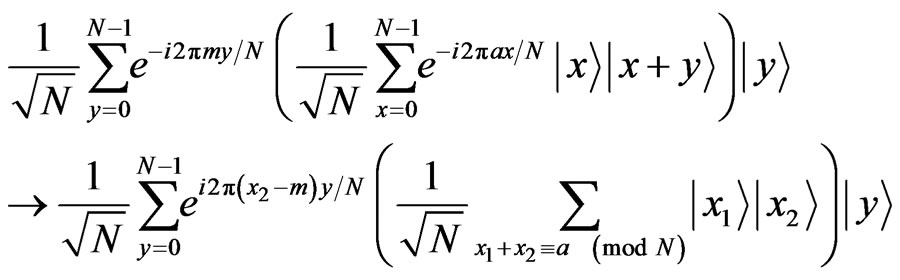
Next, by measuring the first two registers, the third party can obtain only 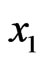 and  satisfying 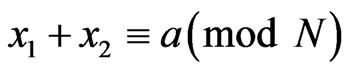 , and obtain the classical message a corresponding to the cover data. After the measurement, the state becomes. Therefore, by applying the quantum Fourier transform to his register and measuring it, Bob can obtain 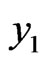satisfying .

In addition, even if any other operation is applied to the stego data, the third party can operate only the state

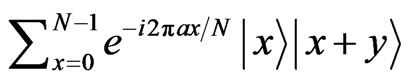corresponding to each state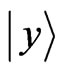

of Bob’s register since Bob has the last register entangled. Then, only Bob can recover the secret message m because it relates to Bob’s register, and the security is held.

5. Conclusions

In this paper we proposed a quantum steganography protocol embedding secret messages to plain text. In general, steganography embedding secret messages to plain text is more difficult than that of other cover data such as image data or audio data since we feel the plain text strange even if the modification is slightly. On the other hand, we can use natural plain text as the cover data used in our steganography protocol. Therefore, any eavesdropper cannot decide whether the message is stego data or not. Moreover, although our protocol must share entangled states between parties in advance as quantum keys used when the parties recover secret messages from stego data, neither innocent-looking information nor the information of any secret message is included in the states.

By using the property that can use any natural plain text, a legitimate party is also able to have cover data made by a third party, i.e., a third party creates a natural text a, and applies the phase 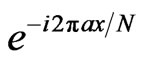of Step 2 in Section 3.

REFERENCES