Journal of Building Construction and Planning Research
Vol.03 No.02(2015), Article ID:56765,7 pages
10.4236/jbcpr.2015.32007
Optimum Design of Tilt Angle and Horizontal Direction of Solar Collectors under Obstacle’s Shadow for Building Applications
Shaoning Wang1, Bo Hong2*
1Department of BIM Center, China Architecture Design Institute Co. Ltd., Beijing, China
2College of Landscape Architecture and Arts, Northwest A&F University, Yangling, China
Email: wang.sn@gmail.com, *hongbo@nwsuaf.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2015; accepted 25 May 2015; published 28 May 2015
ABSTRACT
Solar collectors can provide clean, renewable, and domestic energy. The tilt angle and horizontal direction of solar collectors significantly affect its efficiency. There are many good methods to search the optimum tilt angle and horizontal direction to realize the maximum total radiation on the solar collector within a particular day or a specific period. However, it is hard to realize it when solar collectors are placed under obstacle’s shadows; especially when some obstacles, such as trees, have irregular shapes. This paper presents algorithms to achieve the best tilt angle and horizontal direction for solar collector’s performance under the free-form surfaces 3D obstacle’s shadow. The solution process is composed of 4 steps. First, it creates a 3D scene, in which a unique color is given to the solar collector. Second, it employs orthographic projection from the point of view to get an image of the scene. Third, the number of pixels is used to represent the efficiency of the solar collector by counting the pixels of the unique color. Fourth, the efficiency of solar collector in each direction in a period of time is calculated with many images to further select the best direction.
Keywords:
Solar Collector, Tilt Angle, Horizontal Direction, Solar Radiation, Optimum Design, Orthographic Projection

1. Introduction
Solar collectors including water heaters and solar photovoltaic panels are widely used in China. Chinese government has made renewable energy a keystone of its energy policy and aims to increase solar power capacity tenfold in the next five years. Photovoltaic cells are converted into electrical energy through the photoelectric effect or photochemical effects of light energy. China’s solar cell research started in 1958. In recent years, China has surpassed Europe and Japan and became the world’s solar cell manufacturing superpower in 2012. Solar collector’s tilt angle and horizontal direction should be regulated according to different latitudes and the radiation period of time. With the best tilt angle and horizontal direction, the radiation on the collector surface is a maximum for a particular day or a specific period. The performance optimization of solar collectors in the world has been extensively studied.
In the widely adopted trigonometric algorithm, it is assumed that there is no obstacle which casts shadow on the solar collector. Most solar collectors installed in the northern hemisphere are oriented to south and tilted at a certain angle. If the solar collector is placed under the obstacle’s shadows, it is difficult to calculate the solar collector’s optimum tilt angle and horizontal direction by using trigonometric algorithm.
Orthographic projection from the sun’s point of view provides information about the solar collector’s efficiency [1] . From the sun’s point of view, the part of solar collector that can be seen is exposed to the sun. We set orthographic projection from sun’s point of view to acquire an image. Then, we can “see” what sun can “see”. The orthographic projection from the sun’s point of view can be quickly and efficiently obtained with the modern Z-buffer technology in video card hardware and software. Therefore we could use a simple and useful bitmap technique to avoid complex calculations of trigonometric algorithm [2] . In the model, a unique color is given to the solar collector. The area exposed to the sun can be calculated simply by counting the unique color pixel in the images. As a result, the best direction of solar collector can be selected.
Optimum solar collector’s tilt angle had been widely studied [3] . The best way for solar collector to receive maximum daily energy is to use solar tracking system. It is possible to collect 40% or more solar energy by using a two-axis tracking system [4] [5] . However, the trackers are costly and consume energy during the operation. Therefore, the practicable way is to choose a best direction for solar collectors. Two kinds of factors affect the value of this optimum tilt angle [6] . The first kind of factors includes reflection properties of sky and ground and actual climatic conditions of the site, regarding snow fall and dust. The second kind of factor is the maximization of the amount of collectable radiation in the whole year or a certain period of time. The theoretical and experimental results indicate that the sky radiation is NOT isotropically distributed at all times [7] . Over the last few years, many models were proposed to optimize solar collectors based on the consideration of sky and ground reflection. There are at least three specific anisotropic sky models to deal with diffuse radiation. The main influencing factor of the solar collector is the direct solar radiance [8] - [10] .
It is well known that solar collectors installed in the northern hemisphere must be oriented to south. The tilt angle with the horizontal is the most important factor that affects the performance of the solar collector. The variation of tilt angle changes the amount of solar radiation reaching the collector surface. The optimum tilt angle was proposed based only on the latitude [11] [12] . Many researchers offered answers to many situations. The φ is the latitude of the location and the optimum tilt angle has many values according to different seasons, such as φ + 10˚ ~ 30˚, φ + 10, and φ − 10 [13] [14] . Based on the latitude of the location (φ), some researchers suggest that the optimum tile angle should have two values: φ ± 10˚ and φ ± 8˚ and φ to add for winter and reducing for summer [15] .
The trigonometric algorithm is generally used to optimize solar collectors. Actually, some obstacles often exist between the solar collector and sun. They cast shadows on the solar collector. In a city, solar collectors are always planted on the top of a building, usually avoiding the fact that solar collector is shadowed by the higher buildings nearby. When this happens, not only tilt angle but also horizontal direction should be calculated. Because some obstacles have irregular shapes, it is difficult to calculate the best solar collector’s tile angle and horizontal direction by using traditional methods.
Back to the beginning of the question, the optimum tile angle and horizontal direction mean that within a period of time, this angle allows maximum solar radiation energy. In other words, if solar collector’s efficiency within a certain time under some obstacles was calculated, we could accumulate each time in a period. Some research made an important contribution to solve this problem, but the method was very simple [16] . By drawing an orthographic projection from the sun’s point of view, we can figure out the insolated and the shaded areas of the solar collector; the area on the solar collector that could be seen is exposed to the sun.
A sun position algorithm is required. We adopted an algorithm, which announces solar zenith and azimuth angles in the period from the year −2000 to 6000, with uncertainties of ±0.0003˚ [17] .
2. Methodology
Firstly, confirm that you have the correct template for your paper size. This template has been tailored for output on the custom paper size (21 cm × 28.5 cm). Assuming that the sun collector’s plane has its area (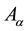 ) and normal direction is
) and normal direction is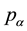 . At a certain moment t, the vector from the solar collector to the sun is
. At a certain moment t, the vector from the solar collector to the sun is  and it just reverses the direction towards the sunlight. θ is the angle between
and it just reverses the direction towards the sunlight. θ is the angle between 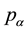 and
and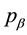 . Therefore,
. Therefore, ’s projection area from the
’s projection area from the  is
is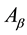 , which is defined as “effective area” (Figure 1).
, which is defined as “effective area” (Figure 1).
So Equation (1) is obtained as:
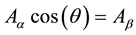 (1)
(1)
If atmosphere is NOT taken into consideration, the solar collector’s efficiency is transformed into the question about the angle (θ) between the vector to the sun and the solar collector’s normal (0˚ < θ < 90˚). When the solar collector is directed to the sun, (θ = 0) solar collector can achieve its maximum efficiency. When θ ≠ 0, the efficiency of the sun collector is reduced to cos(θ) of the maximum efficiency.
2.1. Getting one Moment Solar Collector’s Effective Area
In most of the time, it is not directly facing the sun’s moving position. Therefore, it will lose some efficiency. We can use Equation (1) to get solar collector’s effective area. If there are some kinds of obstacles, such as buildings, trees and any free-form surfaces 3D objects, between the sun and solar collector, it is difficult to use traditional trigonometric formula to calculate solar collector’s effective area.
The simplest way to figure out solar collector’s efficiency is to draw an orthographic projection from the sun’s point of view and turn the 3D scene into an image. The area exposed to the sun can be seen from the image. When obstacle casts a shadow on the solar collector, the shadow area of the solar collector always shows the obstacle’s color. By analyzing the image, collector’s area projected from the sun’s point of view at that time can be acquired (Figure 2).
Figure 1. Tilt angle and horizontal direction of solar collectors.
Figure 2. Orthographic projection and image.
We can get solar collector’s efficiency in 3 steps:
1) To create a 3D scene, and gives solar collector a unique color.
2) To draw the orthogonal projection from the sun’s point of view, a unique color is given to the solar collector and the scene is turned into an image [18] .
3) To count the unique color. The amount of unique color pixels represents the efficiency of solar collector.
Orthographic projection has its “projection window”, in which “width” and “height” are marked as 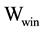 and
and . The solar collector’s width and height can be marked as
. The solar collector’s width and height can be marked as 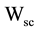 and
and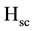 . “Projection window” should be larger than the solar collector:
. “Projection window” should be larger than the solar collector: 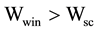 and
and
Width and height of the orthographic projection window are respectively 




The area of orthographic projection is


If there are some obstacles, such as buildings or trees, between sun and solar collector, they will “block” the solar collector in the image. Therefore, this part of solar collector will NOT show solar collector’s unique color, but the obstacle’s own color. Therefore, we can know the shadowed area of the solar collector by reading the color pixel of image. Solar collector’s effective area can be read from the image. It deals with the free-form surfaces 3D model, which holds solar collector’s model and all kinds of obstacles model. If they are 

Trace line of the sun is the approximate arc of a curve.
In the period from sunrise to sunset, we get images from sun’s point of view with fixed time intervals. Each unique color pixel in the image can represent solar collector’s effective area and effective period of time. Solar constant

The energy that solar collector receives from the sun in one period of time can be acquired by counting its pixels in the image which are generated by the orthographic projection. If they are 

2.2. Accumulating Solar Collector’s Efficiency in One Period with One Direction
By accumulating the solar collector’s pixel in many images which have the same interval time in a period, the efficiency of solar collector in a period can be obtained. For example, for a period 



Each image has 


2.3. Searching the Optimum Direction among Many Solar Collector’s Directions
By accumulating many images with the same interval in a period of time, the efficiency of certain tilt angle and horizontal direction can be obtained. Many different directions correspond to many different



3. Results and Discussion
In order to test the new algorithm, we created a program called “solar collector optimizing”.
The program is divided into two parts: the sketch up plugin that gets geometric data from sketch up model and C++ program to detect the optimum angle of solar collectors.
With a model built firstly, we can set the parameters as follows: 1) length and width of a solar collector; 2) latitude and longitude; 3) start date and end date; 4) sampling interval; 5) horizontal search angle range; 6) vertical search angle range; 7) subdivision angle for search.
Moreover, the solar collector’s bottom middle point in the 3D scene should be set. In our study case, it is located in south of Beijing in the eastern China at 38.5˚N and 119˚E. The sampling interval is 10 minutes.
We firstly tested a model without obstacle. In the model, the solar collector was directly facing to the south. Then, we used the program to search the best tilt angle. We calculated the result once every 1˚. We got the results for each month and the whole year.
When there is no obstacle, it is easy to determine the optimum tilt angle of solar collectors for building applications. In previous results [15] , the best tilt angle of solar collector at the latitude 38.46˚N was provided. The latitude is close to our location (38.5˚N) (Figure 3).
Our algorithm can calculate the results for both the cases without obstacles and the scenes with all kinds of obstacles. The number of pixels can be used to measure extraterrestrial solar radiation reaching solar collector.
We tested another model with the same period of time and the same location. However, the solar collectors were installed on the roof of a building surrounded by many buildings as well as an irregular shaped tree (Figure 4 and Figure 5). The results of two models are shown in Table 1.
Comparison of new algorithms and trigonometric algorithms:
1) Precision: The new algorithm will partially decrease the precision because discrete pixels are adopted to express continuous geometry. However, the quantity of pixels in an image is generally more than one million. Therefore, the decrease of the precision is negligible. We can use more intensively sampling rates and shorter
Table 1. Best tilt angle and horizontal direction in Beijing.
Figure 3. Comparison of the results of new algorithm and trigonometric algorithms.
Figure 4. Obstacle scene.
Figure 5. Program-generated images.
intervals to control the precision.
2) Usability: when there is no obstacle, trigonometric algorithm is simple and does not require any model. By simply inputting the location and time, you can calculate the results with the formula. However, in case of obstacles, trigonometric algorithm is very complicated. The new algorithm requires a 3D model.
3) Performance: The performance of the new algorithm is much slower than that of the trigonometric algorithms. The calculation time of traditional algorithm may be neglected, but the calculation time of new algorithm for obtaining a precise result is several hours. The algorithm can be parallelized to improve its speed.
For example, we create an image every 10 minutes from sunrise to sunset, 72 times a day. Therefore, we need to analyze 72 images for one day. It is assumed that horizontal angle optimal range and vertical angle optimal range of the solar collector are respectively 90˚ and 50˚. We make one image every 5˚. To optimize solar collectors in a season (120 days), we need to make 72 × 19 × 11 × 120 = 1805760 images. With modern graphics technology, the analysis task can be quickly performed. Our programs completed this analysis task within 30 minutes.
4. Conclusions
In previous studies, the commonly used algorithm is trigonometric algorithm, which cannot handle complex free-form obstacle objects in the urban environment.
In this paper, with the orthogonal projection algorithm, the best direction of solar collectors during a period of time could be calculated. In a 3D scene with many obstacles, a unique color was given to the solar collector. With the modern graphic technique, the image of the scene in the sun’s point of view could be acquired. By counting unique color pixels in the images, the efficiency of solar collector in one moment could be obtained. Through the analysis of a series of images, the efficiency of a certain direction solar collector during a period of time could be acquired. By comparing the results of different directions, we can find the best direction. Compared with previous results, the new algorithm can handle any situation with 3D model. Compared with the trigonometric algorithms, the new algorithm allows the error less than 2.5%.
Although there may be many factors at play with respect to certain type of solar collectors, for example, PV’s efficiency is also affected by ambient temperature (in turn affecting the back-face surface temperature) together with the solar cell type, while our new algorithm can be extended to a lot of solar radiation and construction- related fields to calculate sunlight energy through the window of during a period of time.
Acknowledgements
This research was supported by the Special Fund Programs of Basic Scientific Research of Northwest A&F University (Grant No.2014YB076).
References
- Penrod, E.B. (1964) Solar Load Analysis by Use of Orthographic Projections and Spherical Trigonometry. Solar Energy, 8, 127-133. http://dx.doi.org/10.1016/0038-092X(64)90073-8
- Capeluto, I.G., Yezioro, A. and Shaviv, E. (2003) Climatic Aspects in Urban Design―A Case Study. Building and Environment, 38, 827-835. http://dx.doi.org/10.1016/0360-5442(81)90061-X
- Moon, S.H., Felton, K.E. and Johnson, A.T. (1981) Optimum Tilt Angles of a Solar Collector. Energy, 6, 895-899. http://dx.doi.org/10.1016/0360-5442(81)90061-X
- Markvart, T. (1994) Solar Electricity. John Wiley & Sons, Chichester.
- Yakup, M.A.B.H.M. and Malik, A.Q. (2001) Optimum Tilt Angle and Orientation for Solar Collector in Brunei Darussalam. Renewable Energy, 24, 223-234. http://dx.doi.org/10.1016/S0960-1481(00)00168-3
- Elminir, H.K., Ghitas, A.E., El-Hussainy, F., Hamid, R., Beheary, M.M. and Abdel-Moneim, K.M. (2006) Optimum Solar Flat-Plate Collector Slope: Case Study for Helwan, Egypt. Energy Conversion and Management, 47, 624-637. http://dx.doi.org/10.1016/j.enconman.2005.05.015
- Dave, J.V. (1977) Validity of the Isotropic-Distribution Approximation in Solar Energy Estimations. Solar Energy, 19, 331-333. http://dx.doi.org/10.1016/0038-092X(77)90002-0
- Temps, R.C. and Coulson, K.L. (1977) Solar Radiation Incident upon Slopes of Different Orientations. Solar Energy, 19, 179-184. http://dx.doi.org/10.1016/0038-092X(77)90056-1
- Perez, R., Stewart, R., Arbogast, C., Seals, R. and Scott, J. (1986) An Anisotropic Hourly Diffuse Radiation Model for Sloping Surfaces: Description, Performance Validation, Site Dependency Evaluation. Solar Energy, 36, 481-497. http://dx.doi.org/10.1016/0038-092X(86)90013-7
- Bugler, J.W. (1977) The Determination of Hourly Isolation on an Inclined Plane Using a Diffuse Irradiance Model Based on Hourly Measured Global Horizontal Isolation. Solar Energy, 19, 477-491. http://dx.doi.org/10.1016/0038-092X(77)90103-7
- Shariah, A., Al-Akhras, M.-A. and Al-Omari, I.A. (2002) Optimizing the Tilt Angle of Solar Collectors. Renewable Energy, 26, 587-598. http://dx.doi.org/10.1016/S0960-1481(01)00106-9
- Ozgenera, O. and Hepbaslib, A. (2005) Performance Analysis of a Solar-Assisted Ground-Source Heat Pump System for Greenhouse Heating: An Experimental Study. Building and Environment, 40, 1040-1050. http://dx.doi.org/10.1016/j.buildenv.2004.08.030
- Löf, G.O.G. and Tybout, R.A. (1973) Cost of House Heating with Solar Energy. Solar Energy, 14, 253-278. http://dx.doi.org/10.1016/0038-092X(73)90094-7
- Heywood, H. (1971) Operating Experiences with Solar Water Heating. Journal of the Institute of Heating, Ventilation and Energy, 39, 63-69.
- Gunerhan, H. and Hepbasli, A. (2007) Determination of the Optimum Tilt Angle of Solar Collectors for Building Applications. Building and Environment, 42, 779-783. http://dx.doi.org/10.1016/j.buildenv.2005.09.012
- Shaviv, E. and Yezioro, A. (1997) Analyzing Mutual Shading among Buildings. Solar Energy, 59, 83-88. http://dx.doi.org/10.1016/S0038-092X(96)00103-X
- Reda, I. and Andreas, A. (2004) Solar Position Algorithm for Solar Radiation Applications. Solar Energy, 76, 577-589. http://dx.doi.org/10.1016/j.solener.2003.12.003
- Kroner, W.M. and Abrey, D. (1985) From the Sun’s Point of View. 10th National Passive Solar Conference, Raleigh.
NOTES
*Corresponding author.








