Open Journal of Statistics
Vol.08 No.03(2018), Article ID:85115,30 pages
10.4236/ojs.2018.83028
Minimum Quadratic Distance Methods Using Grouped Data for Parametric Families of Copulas
Andrew Luong
École d’actuariat, Université Laval, Sainte-Foy, Canada

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 8, 2018; Accepted: June 4, 2018; Published: June 7, 2018
ABSTRACT
Minimum quadratic distance (MQD) methods are used to construct chi-square test statistics for simple and composite hypothesis for parametric families of copulas. The methods aim at grouped data which form a contingency table but by defining a rule to group the data using Quasi-Monte Carlo numbers and two marginal empirical quantiles, the methods can be extended to handle complete data. The rule implicitly defines points on the nonnegative quadrant to form quadratic distances and the similarities of the rule with the use of random cells for classical minimum chi-square methods are indicated. The methods are relatively simple to implement and might be useful for applied works in various fields such as actuarial science.
Keywords:
Influence Functions, Quasi-Monte Carlo Numbers, Chi-Square Tests Statistics, Random Cells, Contingency Tables

1. Introduction
In actuarial science or biostatistics we often encounter bivariate data which are already grouped into cells forming a contingency table, see Partrat [1] (p 225), Gibbons and Chakraborti [2] (p 511-512) for examples, and the primary focus is on dependency study and we only want like to make inference on association parameters of the parametric survival copula used to model the dependency of the two components of the bivariate observations.
For the complete data, in actuarial science or biostatistics usually we assume to have a sample of nonnegative bivariate observations which are independent and identically distributed (iid) as with the bivariate survival function expressible as
(1)
where is the survival copula function, and are the marginal survival functions. The bivariate model with deductibles in actuarial science as given by Klugman and Parsa [3] can be considered as having complete data within this framework as we still have a sample of bivariate observations which are iid.
In this paper, we emphasize nonnegative distributions. So in general we use survival functions and survival copula functions but it is not difficult to see that the statistical procedures developed can be adjusted to handle the situation where we use distribution functions and distribution copula instead of survival function and survival copula. If we use distributions functions then the bivariate distribution function
where the marginal distribution functions are given respectively by and . In the paper by Dobric and Schmid [4] , distributions functions are used as the authors emphasize financial applications instead of actuarial science applications. It is not difficult to see that statistical procedures are similar.
For illustrations, we shall discuss of few examples of parametric model for survival copulas. In general, a survival copula can be viewed as a bivariate survival function but the bivariate sample of observations which is given by the complete data is not drawn directly from this bivariate survival function. This should be taken into account when developing inferences methods even when the data is complete. It is natural to have procedures which provide a unified approach for grouped data and for complete data but must be grouped so a rule for grouping the complete data needs to be specified. We shall see that a rule for grouping the data is equivalent to a rule for choosing points on the nonnegative quadrant. We propose inference procedures which are based on quadratic distance and which lead to chi-square tests statistics for the composite hypothesis.
(2)
with the vector of parameters given by and in most of the applications, we just need one or two parameters and the true vector of parameters for the copula model is denoted by . Also, by copula in general we mean survival copula.
In actuarial science we often encounter grouped data, see Klugman et al. [5] for the univariate case. Inferences procedures for bivariate censored data have been developed by Shih and Louis [6] , see the review paper by Genest et al. [7] but inference procedures for grouped data do not seem to receive attention and furthermore, despite that the chi-square tests statistics that Dobric and Schmid [4] propose to make use of a contingency table, complete data must be available first, and then transformed by the marginal empirical distribution functions, subsequently put into cells of a contingency table. By making use of multinomial distributions which are induced by a contingency table, chi-square tests can be proposed. In practice, if data are gouped into a contingency table without being transformed, then the tests procedures are no longer applicable. They also note that chi-square tests statistics can have good power along some direction of the alternatives yet being simple to apply and might be of interest for practitioners.
We also know that chi-square tests statistics in one dimension might not be consistent in all direction of the alternatives yet due to its simplicity to apply as there is a unique asymptotic chi-square distribution across the composite hypothesis, one can control the size of the test. Depending on the alternatives and by carefully choosing the intervals to partition the real line, chi-square tests can still have good power against some directions of the alternatives and in practice. Often we are primarily concerned about some type of alternatives instead of all alternatives. For these advantages, chi-square tests are still used despite there are more powerful tests such as the Cramer-Von Mises tests, see Greenwood and Nikulin [8] (p 124-126) for power under contaminated mixture distributions alternatives and Lehmann [9] (p 326-329) for discussions on power of chi-square tests which are related to the way to create intervals to group the data in one dimension.
Therefore, if we can retain the advantages of the chi-square tests in two dimensions of having a unique chi-square distribution across the null composite hypothesis and improve on the issue of arbitrariness of a grouping rule, the inference procedures might still be attractive for practitioners as implementing other tests procedures might need extensive simulations to approximate a null distribution which depends on .
In this paper, we would like to develop minimum quadratic distance (MQD) procedures for grouped data and the procedures can be extended to the situation of having complete data and they must be grouped by specifying a rule which make use of the Halton sequence of Quasi-Monte Carlo (QMC) numbers and two empirical quantiles from the two marginal distributions or marginal survival functions. Tests for copula models can be performed using chi-square tests statistics with data already grouped and if complete data is available they can be grouped according a more clearly defined rule. As mentioned earlier, the rule to select cells to group the data is a rule to select points on the nonnegative quadrant to construct quadratic distances. If complete data is available then it is established using QMC methods and based on the idea of selecting points in the nonnegative quadrant so that Cramer-Von Mises distances can be approximated by quadratic distances. The methods can also be applied to Copula models with a singular component when provided that the Copula function is differentiable with respect to the parameters given by . An example of such a copula is the one parameter Marshall Olkin(MO) copula, for discussions on MO copulas, see Dobrowolski and Kumar [10] and Marshall and Olkin [11] .
We briefly list some copula models often encountered in practice. Most of them just have one or two parameters. A subclass of Archimedean copulas has the representation using a generator which is the Laplace transform (LT) of a nonnegative random variable denoted by . The class can be represented as
.
If we specify a gamma LT with , then we have the Clayton or Cook-Johnson copula model
.
If we specify a positive stable LT then we have the positive stable copula model which is also called positive stable frailties model with
,
see Shih and Louis [6] for these families and for simulations from these copulas, and see the algorithms given by Mai and Scherer [12] (p 98-99).
Beside this subclass the one and two parameters Marshall Olkin copula models are also frequently used. The two parameters MO model can be expressed as
if and if ,
.
The model has a singular component and if , the MO copula model just has one parameter and
if and if ,
note that is singular for but a function of , is differentiable. For further discussions on MO copulas see Dobrowolski and Kumar [10] and see Ross [13] (p 103-108) for simulations from MO copulas and Gaussian copulas. The Gaussian Copula model can be represented by
,
with the standard normal univariate quantile function denoted by and the integrand of the above integral is a bivariate normal density function with standard normal marginals and parameter ρ.
Copulas are often used to create bivariate distributions and for inference procedures for these distributions for actuarial science, see Klugman and Parsa [3] , Klugman et al. [14] , Frees and Valdez [15] for examples.
Before giving further details and properties of MQD methods, we shall give the logic behind the MQD procedures.
Let the bivariate empirical survival function be defined as
with being the usual indicator function, let and define the two univariate empirical marginal survival functions as
and ,
we then have the following convergence in probability properties,
with the true survival function and the marginal survival functions are given respectively by , and . We shall assume that and are absolutely continuous, is either absolutely continuous or is absolutely continuous everywhere except when where the survival distribution can be singular as in the case of the bivariate exponential model introduced by Marshall and Olkin [11] .
Now if the parametric survival copula model is valid,
so that
for .
For the time being assume that the M points given by are already chosen, then we can define the vector of empirical components,
with the counterpart vector which makes use of the copula model,
,
and form the vector of differences , by choosing a symmetric positive definite matrix we can form a class of quadratic distances (QD) given by
.
A positive definite matrix can be used to create a weighted Euclidean norm, so we can also let
,
is the weighted Euclidean norm induced by and if we let then we obtain the classical Euclidean norm. QD inferences procedures developed subsequently are based on which are similar to the univariate case. For MQD procedures with univariate observations, see Luong and Thompson [16] .
The paper is organized as follows.
In Section 3, MQD methods will be developed using predetermined grouped data such as data presented using a contingency table. The efficient quadratic distances is derived and can be used for estimation and model testing. Asymptotic theory is established for MQD estimators and chi-square tests using quadratic distances can be constructed for testing copula models. In Section 4, by viewing grouped data as defining a set of points on the nonnegative quadrant, a rule to select points is proposed based on Quasi-Monte-Carlo numbers and two sample quantiles if complete data is available and the methods can be extended to the situation where complete data is available. The methods can be seen as similar to minimum chi-square methods with random cells but with a rule to define these cells. The choice of random cells for minimum chi-square methods is less well defined. Section 5 illustrates the implementations of MQD methods using a limited simulation study by comparing the methods of moment estimator (MM) estimators based on sample Spearman rho which requires the availability of complete data versus the MQD estimator which uses grouped data for the one parameter Marshall-Olkin model and it appears that the chi-square tests have some power to detect alternatives which can be represented as mixture or contaminated copula model such as the mixture of one parameter Marshall-Olkin copula model and Gaussian copula model from the study. The findings appear to be in line with chi-square tests in one dimension which also display similar properties if intervals are chosen properly.
2. MQD Methods Using Grouped Data
2.1. Contingency Tables
Contingency table data can be viewed as a special form of two-dimensional grouped data. We will give some more details about this form of grouped data.
Assume that we have a sample which are independent and identically distributed as which follows a non-negative continuous bivariate distribution with model survival function given by . The marginal survival functions are given respectively by and assumed to be absolutely continuous but there is no parametric model assumed for the marginals.
The vector of parameters is , the true vector of parameters is denoted by . We do not observe the original sample but observations are grouped and put into a contingency table and only the number which fall into each cells of the contingency table are recorded or equivalently the sample proportions which fall into these cells are recorded. Contingency tables are often encountered in actuarial science and biostatistics, see Partrat [1] (p 225), Gibbons and Chakraborti [2] (p 511-512) and we shall give a brief description below.
Let the nonnegative axis X be partitioned into disjoints interval with and similarly, the axis Y be partitioned into disjoints interval with .
The nonnegative quadrant can be partitioned into nonoverlapping cells of the form.
.
The contingency table is formed which can be viewed as a matrix with elements given by
.
The empirical bivariate survival function is as defined earlier with , the underlying bivariate survival distribution. We assume that is either absolutely continuous or it can have a singular component when as in the case of the bivariate exponential distribution of Marshall Olkin [9] but absolutely continuous elsewhere. Implicitly, the marginal survival functions and are assumed to be absolutely continuous.
The sample proportion or empirical probability for one observation which falls into cell can be obtained using
(3)
and the corresponding probability using the copula model coupled with the empirical survival distributions and with is given by
.
It is not difficult to see that there is redundant information displayed by a contingency table, one way to see that there is duplication is to note
(4)
and similarly, .
Therefore, the set points given by can be discarded without affecting the information provided by the contingency table. Consequently, we can view a contingency table implicitly define a grid on the nonnegative quadrant with only points. It is also clear that if we want a rule to choose cells, the same rule will allow us to choose points on the nonnegative quadrant.
The objective function of the proposed quadratic form will be given below. It is a natural extension of the objective function used in the univariate case. Define a vector with empirical components so that we only need one subscript by collapsing the points of the contingency table given by
into a vector by putting the first row of the matrix as the first batch of elements of the vector and the second row being the second batch of elements so forth so on, i.e., let
. (5)
and its counterpart which makes use of the copula model is
. (6)
The number of components of is M with the assumption .
A class of quadratic distances can be defined as
(7)
with being a symmetric and positive definite matrix. In this class, we focus on two choices of .
Letting , we obtain the unweighted quadratic distance, this choice is not optimum but it produces consistent estimators and can be used as preliminary estimates for to start the numerical procedures for finding more efficient estimators. The matrix is defined up to a positive constant as minimizing the objective function multiplied by a positive constant still gives the same estimators and a consistent estimate of can be used to replace without affecting the asymptotic theory for estimation and asymptotic distribution for test statistics. Using quadratic distance theory or generalized methods of moment (GMM) theory, it is not difficult to see that an optimum choice for is to let where and is an asymptotic covariance matrix which is given by
see Remark 2.4.3 given by Luong and Thompson [16] (p 245).
Clearly, depends on . We shall obtain the expression for and show that can be estimated by in the next section as we can obtain a preliminary consistent estimate for by using the unweighted quadratic distance or other quick methods; see the methods of moment using Spearman-rho in Section 5.2 for example. Consequently, by quadratic distance we mean the following efficient version with the objective function defined as
with . (8)
The version with will be called unweighted quadratic distance. In the next section we shall use the influence function representation for to derive and we shall also propose a consistent estimate for .
2.2. Optimum Matrix W0
The matrix which is the asymptotic covariance matrix of the vector plays an important role for MQD methods as we can obtain estimators with good efficiencies for estimators using or a consistent estimate of and we also have chi-square tests statistics. Despite that is unknown, its elements are not complicated and moreover, it can be replaced by a consistent estimate without affecting the asymptotic properties of the procedures. We shall give more details about this matrix and construct , a consistent estimate of .
Using influence representation for the vector of functions of which depend on three functions as discussed by Reid [17] , see technical appendix (TA1) in the Appendices for more details, it can be seen that is the covariance matrix of the vector under with
,
,
and is the usual indicator function,
, .
are respectively the partial derivatives of with respect to u and v.
It is not difficult to see that the elements of are
with and since and are not identically distributed is not symmetric, the matrix has 9 elements, see technical Appendix (TA2) in the Appendices for more details. The elements can be expressed as
(9)
The elements can be estimated empirically by replacing in the expressions of by for . The estimates can be formed.
Therefore, we can form which estimates . Similarly, by replacing by a consistent preliminary estimate which can be obtained using the unweighted quadratic distance for example and replacing by we can estimate by .
an estimate for will have the elements given by
(10)
and define . will be used as an optimum matrix for constructing quadratic distance as the asymptotic property remain unchanged. We can replace the unknown matrix by its consitent estimate which is without affecting asymptotic theory for estimation and tests.
3. MQD Methods Using Grouped Data
3.1. Estimation
The MQD estimators can be seen as given by the vector which minimizes
. (11)
and since
, (12)
, (13)
, (14)
,
we can also used the weighted Euclidean norm with the use of and let
. (15)
Consistency for quadratic distance estimators using predetermined grouped data or if complete data is available but must be grouped according a rule can be treated in a unified way using the following Theorem 1 which is essentially Theorem 3.1 of Pakes and Pollard [18] (p 1038) and the proof has been given by the authors. In fact, their Theorems 3.1 and 3.3 are also useful for Section 4 where we have complete data and we have choices to group the data into cells or equivalently forming the artificial sample points on the nonnegative quadrant to form the quadratic distances.
Theorem 1 (Consistency)
Under the following conditions converges in probability to :
1) , the parameter space Ω is compact
2) ,
3) for each .
Theorem 3.1 states condition b) as but in the proof the authors just use so we state condition b) as .
An expression is if it converges to 0 in probability, if it is
bounded in probability and if it converges to 0 in probability faster than . We have occurs at the values of the vector values of the MQD estimators, so the conditions 1) and 2) are satisfied for both versions. Implicitly, we make the assumption that the parameter space Ω is compact. Also, for both versions only at in general if the number of components of is greater than the number of parameters of the model, i.e., .
For we have for some since survival functions evaluated at points are components of and these functions are bounded. This implies that there exist real numbers u and v with such that
as .
Therefore, the minimum quadratic distance (MQD) estimators are consistent, i.e., . The Theorem 3.1 given by Pakes and Pollard [18] (p 1038-1039) is an elegant theorem using the norm concept of functional analysis. Now we turn our attention to the question of asymptotic normality for the quadratic distance estimators and it is possible to have unified approach using their Theorem 3.3, see Pakes and Pollard [18] (p 1040-1043) where we shall restate their Theorem as Theorem 2 and Corollary 1 given subsequently after the following discussions on the ideas behind their theorem, allowing us to get asymptotic normality results for estimators obtained from extremum of a smooth or nonsmooth objective function.
Note that (16)
with
. (17)
The points are predetermined by a contingency table we give and we have no choice but to analyze the grouped data as they are presented.
Note that is non-random and if we assume is differentiable with repect to with derivative matrix , then we can define the random function to approximate with
. (18)
By using which is the partial derivative of with repect to , the matrix can be displayed explicitly as
. (19)
Note that is differentiable and a quadratic function of , the vector which minimizes can be obtained explicitly with
(20)
and since . is assumed to be a positive define matrix; we have
(21)
Clearly set up fits into the scopes of their Theorem 3.3 where we shall rearrange the results to make them more suitable for MQD methods and verify that we can satisfy the regularity conditions of Theorem 3.3. We shall state Theorem 2 and Corollary 1 below which are essentially their Theorem (3.3) and the proofs have been given by Pakes and Pollard [18] . Note that the condition 4) is slightly more stringent but simpler to check than the condition 3) in their Theorem.
Theorem 2
Let be a vector of consistent estimators for , the unique vector which satisfies .
Under the following conditions:
1) The parameter space Ω is compact, is an interior point of Ω.
2)
3) is differentiable at with a derivative matrix of full rank.
4) for every sequence of positive numbers which converge to zero.
5) .
6) is an interior point of Ω.
Then, we have the following representation which will give the asymptotic distribution of in Corollary 1, i.e.,
, (21)
or equivalently, using equality in distribution,
(22)
or equivalently,
(23)
The proofs of these results follow the results used to prove Theorem 3.3 given by Pakes and Pollard [18] (p 1040-1043). For expression (22) or expression (23) to hold, in general only condition 5) of Theorem 2 is needed and there is no need to assume that has an asymptotic distribution. From the results of Theorem 2, it is easy to see that we can obtain the main result of the following Corollary 1 which gives the asymptotic covariance matrix for the quadratic distance estimators for both versions.
Corollary 1
Let , if then with
, (24)
The matrices and depend on , we also adopt the notations .
We observe that when applying condition 4) of Theorem 2 to MQD methods in general involves technicalities. Note that to verify the condition 4, it is equivalent to verify
, (25)
a regularity condition for the approximation is of the right order which implies the condition 3 given by their Theorem 3.3, which might be the most difficult to check. The rest of the conditions for Theorem 2 are satisfied in general.
Let
(26)
and define which can be expressed as
(27)
Consequently, can also be expressed as
.
Since the elements of are bounded in probability, it is not difficult to see that the sequence is bounded in probability and continuous in probability with as . Also note that . Therefore, results given in section of Luong et al. [19] (p 218) can be used to justify the sequence of functions. attains its maximum on the compact set in probability and hence has the property as and .
Since .
Using results of Corollary 1, we have asymptotic normality for the MQD estimators which is given by
, (28)
as given by expression (19) can be estimated once the parameters are estimated.
3.2. Model Testing
3.2.1. Simple Hypothesis
In this section, the quadratic distance will be used to construct goodness of fit test statistics for the simple hypothesis
H0: data coming from a specified distribution with distribution
,
is specified. The chi-square test statistic with its chi-square asymptotic distribution and its degree of freedom
. (29)
It is not difficult to see that indeed we have the above asymptotic chi-square distribution as and
,
, using standard results for distribution of quadratic forms,
3.2.2. Composite Hypothesis
The quadratic distances can also be used for construction of the test satistics for the composite hypothesis
H0: data comes from a parametric model .The chi-square test statistic and its asymptotic distribution are given similarly in this case by
, (30)
with .To justify the asymptotic chi-square distribution given above, note that we have the equality in probability, . It suffices to consider the asymptotic distribution of as we also have the following equalities in distribution,
,
as given by expression. Therefore we also have the following equalities in distribution, which can be reexpressed as
or equivalently, with .
We have
,
(31)
and note that and the trace of the matrix is ; the rank of the matrix is also equal to its trace using the techniques as given by Luong and Thompson [16] (p 248-249).
4. Estimation and Model Testing Using Complete Data
4.1. Preliminaries
In Section 4.1 and Section 4.2, we shall define a rule of selecting the points if complete data are available. Selecting points is equivalent to define the cells used to group the data and we shall see that random cells will be used as the points constructed using Quasi-Monte Carlo (QMC) numbers on the unit square multiplied by two chosen sample quantiles from the two marginal distributions will be used. They are random and can be viewed as sample points on the nonnegative quadrant forming an artificial sample. For minimum chi-square methods it appears to be difficult to have a rule to choose cells to group the data, see discussions by Greenwood and Nikulin [8] (p 194-208). We need a few preliminary notions tools and define sample quantiles then statistics can be viewed as functionals of the sample distribution; the notion of influence function is also introduced and this useful tool will be used to find their asymptotic variance of the functional.
We shall define the pth sample quantile of a distribution as we shall need two sample quantiles from the marginal distributions together with QMC numbers to construct an approximation of an integral. Our quadratic distance based on selected points can be viewed as an approximation of a continuous version given by an integral as given by expression (33).
From a bivariate distribution we have two marginal distributions and . The univariate sample pth quantile of the distribution assumed to be continuous is based the sample distribution function
and it is defined to be and its model counterpart is given by . We also use the notation and . We define similarly the qth sample quantile for the distribution as and its model counterpart with .
The sample survival function is defined as
The sample quantile functions or can be viewed as statistical functionals of the form with or . The influence function of is a valuable tool to study the asymptotic properties of the statistical functional and will be introduced below. Let H be the true distribution and is the usual empirical distribution which estimates H; also let be the degenerate distribution at x, i.e., if and , otherwise; the influence function of T viewed as a function of x, is defined as a functional directional derivative at H in the direction of . Letting , is defined as
and is a linear functional.
Alternatively, it is easy to see that and this gives a convenient way to compute the influence function. It can be shown that the influence function of the pth sample quantile is given by
and
with h being the density function of the distribution H which is assumed to be absolutely continuous, see Huber [20] (p 56), Hogg et al. [21] (p 593). A statistical functional with bounded influence function is considered to be robust, B-robust and consequently the pth sample quantile is robust. The sample quantiles are robust statistics.
Furthermore, as is based on a linear functional, the asymptotic variance of is simply with being the variance of
the expression inside the bracket since in general we have and we have following representation when is bounded as a function of ,
and ,
, see Hogg et al. [21] (p 593). Consequently, in general we have for bounded influence functional with the use of means of central limit theorems (CLT) the following convergence in distribution
, .
The influence function representation of a functional which depends only on one function such as is the equivalence of a Taylor expansion of a univariate function and the influence function representation of a functional which depends on many functions is the equivalence of a Taylor expansion of a multivariate function with domain in an Euclidean space and having range being the real line. Since we work with marginal survival functions, we define the pth sample quantiles of the marginals survival functions as
.
The influence functions for and can be derived using the definitions of influence functions or obtained from the influence functions of and .
Subsequently, we shall introduce the Halton sequences with the bases and and the first M terms are denoted by
.
We also use to denote set of points . The sequence of points belong to the unit square can be obtained as follows.
For , we divide the interval into half ( ) then in fourth
( ) so forth so on to obtain the sequence .
For
, we divide the interval
Note that the Halton sequence of numbers are deterministic and useful for approximating an integral, if we would like to compute numerically an integral of the form with being a bivariate function. Using the M terms of the Halton sequence and QMC principles, it can be approximated as
. (32)
but if we are used to integration by simulation we might want to think the M terms represent a quasi random sample of size M from a bivariate uniform distribution which is useful for approximating A.
From observations which are given by iid with common bivariate survival distribution . Let the two marginal survival functions be denoted by and and they are absolutely continuous by assumption; also define the bivariate empirical distribution function which is similar to the bivariate empirical survival function as
.
The two empirical marginal survival functions are defined respectively by
and .
We might want to think that we would like to approximate the following Cramer-Von Mises distance expressed as an integral given by
(33)
which is similar to univariate Cramér-Von Mises (CVM) distance and minimizing the distance with respect to will give the CVM estimator for , see Luong and Blier-Wong [24] for CVM estimation for example.
In the next section we shall give details on how to form a type of quasi sample or artificial sample of size M using the
. (34)
We can see the expression (34) is an unweighted quadratic distance using the identity matrix as weight matrix instead of . The unweighted quadratic distance still produces consistent estimators but possibly less efficient estimators than estimators using the quadratic distance with for large samples and for finite samples the estimators obtained using might still have reasonable performances and yet being simple to obtained.
The set of points is a set of points proposed to be used to form optimum quadratic distances in case that complete data is available. We shall see the set of points depend on two quantiles chosen from the two marginal distributions and they are random consequently. We might want to think that we end up working with random cells.
As for the minimum chi-square methods if random cells stabilize into fixed cells minimum chi-square methods in general have the same efficiency as based on stabilized fixed cells, see Pollard [25] (p 324-326) and Moore and Spruill [26] for the notion of random cells; quadratic distance methods will share the same properties. The chosen points are random but it will be shown that they do stabilize and therefore these random points can be viewed as fixed at stabilized points and despite that they are random, it does not affect efficiencies of the estimators or asymptotic distributions of goodness-of-fit test statistics which make use of them. These properties will be further discussed and studied in more details in the next section along with the introduction of an artificial sample of size M given by the points on the nonegative quadrant which give us a guideline on how to choose points if complete data is available.
4.2. Halton Sequences and an Artificial Sample
From the M terms of the Halton sequences, we have .
Let and , we can form the artificial sample with elements given by with with . Note that we have the following relationships between empirical quantile based on distributions and survival functions with and .
We can view being a form of quasi random sample on the nonnegative quadrant and these are the points proposed to be used in case of complete data is available. In general, we might want to choose if and if n is small we try to ensure . Consequently as , M remains bounded. If , there might be difficulty to obtain the matrix as might be nearly singular. In practice we tend to replace by a near optimum matrix obtained from by regularizing the eigenvalues of which might not be stable which causes the matrix to be nearly singular hence will not be available; see Section 5.1 for more discussions on these issues.
Since
and
,
with
and 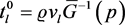 for
and the points
are non-random or fixed.
for
and the points
are non-random or fixed.
It turns out that quadratic distances for both versions constructed with the points are asymptotic equivalent to quadratic distances using the points so that asymptotic theory developed using the points considered to be fixed continue to be valid; we shall show indeed this is the case. Similar conclusions have been established for the minimum chi-square methods with the use of random cells provide that these cells stabilize to fixed cells, see Theorem 2 given by Pollard [25] (p 324-326). We shall define a few notations to make the arguments easier to follow.
Define and similarly let
.
We work with the quadratic distance defined using which leads to consider quadratic of the form . Now to emphasize and which depend on , we also use respectively the notations and and define
.
It suffices to verify that results of Theorem 1, Theorem 2 and its corollary in Section 3 continue to hold.
Observe that we have
(35)
and
(36)
.
This also means that we have the same limit in probability for and as we have and .
Clearly, .
It remains to establish .
Using results on the influence functions representations for functionals as discussed, it suffices to show that the vector has the same influence representation as the vector to conclude that all the asymptotic results are valid even are random.
We shall derive the influence functions for elements of the vector of functional and show that they are the same for the corresponding elements of the vector of functional . Let be the true bivariate survival function and under the parametric model being considered, and we also use the notation .
Let be the degenerate bivariate survival function at the point , i.e., if and and , otherwise.
Let the degenerate survival function at x be defined as
if
and
, otherwise. Similarly, let the degenerate survival function at
which is a contaminated bivariate survival function and
Similarly for the marginals,
Now, we consider the jth element of , with each
Clearly, depend on and
but we can use the influence function representation of , a technique proposed by Reid [29] (p 80-81) but in this case it will need three influence functions which are given by
which is bounded with respect to ,
and the expression is reduced to
by noting the first two terms of the the RHS of the above expression cancel each other since we have which implies
.
Similarly,
If we compare with the corresponding jth term of given by the functional , we can verify the functional has the same influence functions as the functional . It is not difficult to see that we have the equalities
Therefore, all the asymptotic results of Section 3 remain valid and all these influence functions are bounded so that inference methods making use of these functionals are robust in general. Furthermore, we can consider the inference procedures based on quadratic distances as we have non-random points if they can be replaced by without affecting the asymptotic results already established in Section 3. For more discussions on random cells and influence function techniques for minimum chi-square methods and related quadratic distance methods, see Luong [27] .
5. Numerical Issues and a Limited Study
5.1. Numerical Issues
In this section we shall consider the numerical problem of not being able to obtain the matrix as might be nearly singular and we need to replace by a near optimum matrix obtained from .The techniques of regularizing a matrix have been introduced by Carrasco and Florens [28] (p 809-810) for GMM estimation with continuum moment conditions, MQD methods can be viewed as similar to GMM with a finite number of moment conditions and clearly the techniques can also be applied for MQD methods. We use the spectral decomposition of to obtain its eigenvalues and eigenvectors, see Hogg et al. [21] (p 179) for the spectral decomposition of a symmetric positive definite matrix which allows us to express
where the are positive eigenvalues with corresponding eigenvectors given by the of the matrix . Now, observe that
is not obtainable numerically. It is due to the eigenvalues which are not stable, the regularization of will lead to the following matrix which hopefully is obtainable and approximate . It consists of perturbing the by a small positive number a and define the approximate optimum matrix as
.
Carrasco and Florens [28] (p 809-810) for GMM estimation with continuum moment conditions have shown that asymptotic theory remains unchanged if at a suitable rate as . This condition is difficult to verify in practice. However, we might want to continue to use the asymptotic theory in an approximate sense, i.e., we can replace by and view such a replacement does not modify the asymptotic theory in practice.
A more rigorous approach to justify the chi-square distribution for goodness of fit tests is to divide into 2 steps, first using to construct the distance for estimation and letting be the vector which minimizes
.
Using Equation (31) we have
, ,
also see expression (3.4.2) given by Luong and Thompson [16] (p 248). The matrices and are respectively consistent estimates of and .
It suffices to find the Moore-Penrose generalized inverse of and construct the test statistics as
.
The asymptotic distribution of the test statistics will be again chi-square with degree of freedom using distribution theory for quadratic forms, see Luong and Thompson [16] (p 247) for example and for generalized inverses, see Harville [29] (p 493-514).
Note that if can be used for estimation then we can let , i.e. there is no need to use two quadratic distances separately.
5.2. A Limited Simulation Study
For the study, we fix the number of points . The two samples quantiles are 0.99 quantiles or 0.01 survival functions quantiles if marginal empirical survival functions are used instead of distribution functions for estimation without construction of goodness-of-fit tests. The points used are constructed using the procedures given in Section 4.2. We consider the one parameter MO copula model with
if and if . (37)
is differentiable with respect to and is singular if and see Dobrowolski and Kumar [10] (p 2). For this model, the model
Spearman rho , see Dobrowolski and Kumar [10] (p 5).
The sample Spearman rho is simply the Pearson correlation coefficient but computed using ranks of the observations from the two empirical marginal distributions, see Conover [30] (p 314-318).
If complete data are available, equating gives the moment estimator
and one might expect that the moment estimator has reasonable efficiency as we only has one parameter in this model and the estimate is based on ranks.
The moment estimate can be used to compute which is needed for chi-square tests and for estimation using quadratic distances. We use and there is no problem on inverting the matrix . Clearly if data is already grouped we can use the unweighted quadratic distance to provide a consistent preliminary estimate for . The efficient MQD estimator is denoted by . In the simulation study since we have so many marginal survival functions which can be used so we decide to draw observations directly from the Copula Models. This is not what happens in real life situation but we want to test the procedures. We do not have the computing resources for a large scale study and try various marginal survival functions. More works need to be done but we want to illustrate the procedures.
We use sample size and the number of samples used is . For comparison of of MQD estimator versus Methods of moment (MM) estimator we use the ratio of relative efficiency
where the mean square error of an estimator for is defined as
,
which can be estimated using M samples each of size n.
The unweighted QD estimator is denoted by as the identity matrix I is used for the unweighted quadratic distance. The corresponding
can similarly be used for comparison and it can be estimated using simulated samples.
The range of parameter being considered is , the results are summarized using the first table of Table 1 where we find that the MM estimator and the two quadratic distance estimators have practically equal efficiency up to 4 or 5 decimal precisions.
To study the size of the chi-square tests and the power of the tests let H0: The MO copula model with as given by expression (37) and . With , . Observations are drawn from the model specified by by which specifies the model is a contaminated one given by
is as defined earlier, is the Gaussian copula defined as
with .
Procedures to simulate from Gaussian and MO copulas are given in chapter 6 by Ross [13] (p 97-108). We use and , the sample size
(a)Power study using M = 25 points, n = 3000 and the alternative hypothesis specified as the contaminated model
, 0 < λ < 1.
(b)Critical point for the test using the 95th percentile of a chi-square distribution, χ 0.95 2 ( 24 ) = 36.41 .Power study using M = 35 points, n = 3000 and the alternative hypothesis specified as the contaminated model ( 1 − λ ) C M O ( u , v ) + λ C G a u s s i a n ( u , v ) , 0 < λ < 1.
Table 1. Asymptotic relative efficiencies comparisons for MQD estimators versus MM estimator using N = 1000 samples of size n = 1000 for the one parameter MO copula Model.
Critical point for the test using the 95th percentile of a chi-square distribution, .
and we use . Dobric and Schmid [6] (p 1060-1061) in their study have used and their chi-square tests have around 70 degrees of freedom. With only occasionally that is nearly singular, if this happens we discard the sample. We do not have resources for larger scale study; each run takes around three minutes to complete. As most of the time we are drawing observations using an alternative model but for testing we must estimate the parameter of the MO model, the algorithm tends to take time to converge. The study is very limited as the number of simulated samples is small with and only a few copula models are considered but it seems to point to the potential uses of MQD chi-square tests. The tests especially with seem to have power especially along some directions which can be represented as a mixture type of models as shown by the means and standard deviations of the chi-square statistics as displayed in the second and third table of Table 1. More simulation works are needed to assess the power of the MQD tests using various copula models. There are not many statistical procedures for copula models using data that have been already grouped. MQD methods might be useful for this type of situation.
6. Conclusions
Minimum Quadratic Distance Methods (MQD) offer a unified for estimation and model testing using grouped data under the form of a contingency table for parametric copula models without having to assume parametric models for the marginal distributions. The methods share with minimum chi-square methods by having a unique asymptotic distribution across the composite hypothesis for testing which make the implementations relatively simple without requiring extensive simulations for approximating the null asymptotic distribution. It is shown in this paper that if complete data are available, a rule to define points based on QMC numbers can be proposed to alleviate the arbitrariness on the choice of points to construct quadratic distances. The rule will also make quadratic distances close to Cramer-Von Mises distances. It is well known that in one dimension, chi-square tests cannot be consistent against all alternatives but if the intervals are chosen properly the tests still can have good power against some form of alternatives considered to be useful for applications.
MQD tests statistics with the rule of choosing points might preserve the same properties and by being relative simple to implement, they can be useful for applied works. More numerical and simulation works are needed for further study the power of the MQD tests.
Acknowledgements
The helpful and constructive comments of a referee which lead to an improvement of the presentation of the paper and support form the editorial staffs of Open Journal of Statistics to process the paper are all gratefully acknowledged.
Cite this paper
Luong, A. (2018) Minimum Quadratic Distance Methods Using Grouped Data for Parametric Families of Copulas. Open Journal of Statistics, 8, 427-456. https://doi.org/10.4236/ojs.2018.83028
References
- 1. Partrat, C. (1995) Compound Model for Two Dependent Kinds of Claims. Insurance: Mathematics and Economics, 15, 219-231. https://doi.org/10.1016/0167-6687(94)90796-X
- 2. Gibbons, J.D. and Chakraborti, S. (2011) Nonparametric Statistical Inference. 5th Edition, CRC Press, Boca Raton. https://doi.org/10.1007/978-3-642-04898-2_420
- 3. Klugman, S.A. and Parsa, A. (1999) Fitting Bivariate Distributions with Copulas. Insurance: Mathematics and Economics, 24, 139-148. https://doi.org/10.1016/S0167-6687(98)00039-0
- 4. Dobric, J. and Schmid, F. (2005) Testing Goodness of Fit for Parametric Families of Copulas—Applications to Financial Data. Communications in Statistics: Simulation and Computation, 34, 1053-1068. https://doi.org/10.1080/03610910500308685
- 5. Klugman, S.A., Panjer, H.H. and Willmot, G.E. (2012) Loss Models: From Data to Decisions. Wiley, New York.
- 6. Shih, J.H. and Louis, T.A. (1995) Inferences on the Association Parameter in Copula Models for Bivariate Survival Data. Biometrics, 51, 1384-1399. https://doi.org/10.2307/2533269
- 7. Genest, C., Rémillard, B. and Beaudoin, D. (2009) Goodness-of-Fit Tests for Copulas: A Review and Power Study. Insurance: Mathematics and Economics, 44, 199-213. https://doi.org/10.1016/j.insmatheco.2007.10.005
- 8. Greenwood, P. and Nikulin, M.S. (1996) A Guide to Chi-Square Testing. Wiley, New York.
- 9. Lehmann, E.L. (1999) Elements of Large Sample Theory. Springer, New York. https://doi.org/10.1007/b98855
- 10. Dobrowolski, E. and Kumar, P. (2014) Some Properties of the Marshall-Olkin and Generalized Cuadras-Augé Families of Copulas. The Australian Journal of Mathematical Analysis and Applications, 11, 1-13.
- 11. Marshall, A.W. and Olkin, I. (1967) A Multivariate Exponential Distribution. Journal of the American Statistical Association, 62, 30-44. https://doi.org/10.1080/01621459.1967.10482885
- 12. Mai, J.-F. and Scherer, M. (2012) Simulating Copulas: Stochastic Models, Sampling Algorithms and Applications. Imperial College Press, London. https://doi.org/10.1142/p842
- 13. Ross, S.M. (2012) Simulations. 5th Edition, Elsevier, New York.
- 14. Klugman, S.A., Panjer, H.H. and Willmot, G.E. (2012) Loss Models: Further Topics. Wiley, New York.
- 15. Frees, E.W. and Valdez, E.A. (1998) Understanding Relationships Using Copulas. North American Actuarial Journal, 2, 1-25.
- 16. Luong, A. and Thompson, M.E. (1987) Minimum-Distance Methods Based on Quadratic Distances for Transforms. Canadian Journal of Statistics, 15, 239-251. https://doi.org/10.2307/3314914
- 17. Reid, N. (1981) Influence Functions for Censored Data. Annals of Statistics, 9, 78-92. https://doi.org/10.1214/aos/1176345334
- 18. Pakes, A. and Pollard, D. (1989) Simulation Asymptotic of Optimization Estimators. Econometrica, 57, 1027-1057. https://doi.org/10.2307/1913622
- 19. Luong, A., Bilodeau, C. and Blier-Wong, C. (2018) Simulated Minimum Hellinger Distance Inference Methods for Count Data. Open Journal of Statistics, 8, 187-219. https://doi.org/10.4236/ojs.2018.81012
- 20. Huber, P. (1981) Robust Statistics. Wiley, New York. https://doi.org/10.1002/0471725250
- 21. Hogg, R.V, McKean, J.W. and Craig, A.T. (2013) Introduction to Mathematical Statistics. Pearson, New York.
- 22. Glasserman, P. (2003) Monte Carlo Methods in Financial Engineering. Springer, New York. https://doi.org/10.1007/978-0-387-21617-1
- 23. Halton, J. (1960) On the Efficiency of Certain Quasi Random Sequences of Points in evaluating Multi-Dimensional Integrals. Numerische Mathematik, 2, 84-90. https://doi.org/10.1007/BF01386213
- 24. Luong, A. and Blier-Wong, C. (2017) Simulated Minimum Cramér-Von Mises Distance Estimation for Some Actuarial and Financial Models. Open Journal of Statistics, 7, 815-833. https://doi.org/10.4236/ojs.2017.75058
- 25. Pollard, D. (1979) General Chi-Square Goodness-of-Fit Tests with Data Dependent Cells. Probability and Related Fields, 50, 317-331. https://doi.org/10.1007/BF00534153
- 26. Moore, D.S. and Spruill, M.C. (1975) Unified Large-Sample Theory of General Chi-Squared Statistics for Tests of Fit. Annals of Statistics, 3, 599-616. https://doi.org/10.1214/aos/1176343125
- 27. Luong, A. (2018) Simulated Quadratic Distance Methods Using Grouped Data for Some Bivariate Continuous Models. Open Journal of Statistics, 8, Article ID: 84193. https://doi.org/10.4236/ojs.2018.82024
- 28. Carrasco, M. and Florens, J.-P. (2000) Generalization of GMM to a Continuum of Moment Conditions. Econometric Theory, 16, 797-834. https://doi.org/10.1017/S0266466600166010
- 29. Harville, D.A. (1997) Matrix Algebra from a Statistician Perspective. Springer, New York. https://doi.org/10.1007/b98818
- 30. Conover, W.J. (1999) Practical Nonparametric Statistics. Wiley, New York.
Appendices
Technical Appendix 1 (TA1)
In this technical appendix, we shall consider influence function representation for the vector of functionals to justify the expression. is as given by expression (9) in Section 3.2.
Let ,
consider the l-th element of , it is given by
which is a functional which depend on three functions but we still can applied the techniques given by Reid [17] (p 80) to have an influence representation of the functional. Since it depends on three functions we shall have three coresponding influence functions. Let with if and and , elsewhere; also, similarly let with if and , elsewhere and let with if and , elsewhere, with . Consequently,
and .
The three influence functions are given respectively by
Consequently, we have the influence representation for the l-th element of with
and since are iid we have the equality in distribution asymptotically,
Equivalently, using vector notations we have the following equality in distribution asymptotically by letting
,
.
, a result which is needed in Section 3.2.
Technical Appendix 2 (TA2)
In this technical appendix, we shall justify the validity of expression (9) of Section 3.2.
The covariance matrix is defined as , the vector
and
.
Therefore the elements of the matrix are given by
Now, note that the above equalities which give the elements of the matrix can be reexpressed as the equalities as given by expression (9) in Section 3.2.


