Open Journal of Statistics
Vol.05 No.06(2015), Article ID:60252,8 pages
10.4236/ojs.2015.56052
Bootstrap Confidence Intervals for Proportions of Unequal Sized Groups Adjusted for Overdispersion
Olivia Wanjeri Mwangi, Ali Islam, Orawo Luke
Department of Mathematics, Egerton University, Njoro, Kenya
Email: owanjeri@yahoo.com, asislam54@yahoo.com, orawo2000@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 August 2015; accepted 8 October 2015; published 13 October 2015
ABSTRACT
Group testing is a method of pooling a number of units together and performing a single test on the resulting group. It is an appealing option when few individual units are thought to be infected leading to reduced costs of testing as compared to individually testing the units. Group testing aims to identify the positive groups in all the groups tested or to estimate the proportion of positives (p) in a population. Interval estimation methods of the proportions in group testing for unequal group sizes adjusted for overdispersion have been examined. Lately improvement in statistical methods allows the construction of highly accurate confidence intervals (CIs). The aim here is to apply group testing for estimation and generate highly accurate Bootstrap confidence intervals (CIs) for the proportion of defective or positive units in particular. This study provided a comparison of several proven methods of constructing CIs for a binomial proportion after adjusting for overdispersion in group testing with groups of unequal sizes. Bootstrap resampling was applied on data simulated from binomial distribution, and confidence intervals with high coverage probabilities were produced. This data was assumed to be overdispersed and independent between groups but correlated within these groups. Interval estimation methods based on the Wald, the Logit and Complementary log-log (CLL) functions were considered. The criterion used in the comparisons is mainly the coverage probabilities attained by nominal 95% CIs, though interval width is also regarded. Bootstrapping produced CIs with high coverage probabilities for each of the three interval methods.
Keywords:
Group Testing, Overdispersion, Quasi-Likelihood, Confidence Interval, Bootstrapping, Coverage Probability

1. Introduction
Group testing started or originated with [1] during World War II as a frugal method of testing blood specimens of army inductees in order to detect the presence of infection. Group testing has been applied in many areas: plant disease assessment [2] , fisheries [3] , quality control, drug discovery and transmission of viruses by insect vectors [4] . It has also been used to screen the population for the presence of HIV/Aids antibody [5] . [1] proposed that, rather than testing each blood specimen individually, portions each of k specimens can be pooled and the pooled specimen can be tested. If the pooled specimen is free of infection, all k inductees are passed with no further tests, otherwise the remaining portions of each of the blood specimens are to be tested individually. If the prevalence of infection is low, the expected number of tests per inductee and thus the expected cost per inductee, would be reduced. [1] assumed that tests were perfect, that is, a negative reading indicated the group contained no defective item and a positive reading indicated the presence of at least one defective item.
Group tests save resources since many units are tested without testing them individually. One of their advantages as a method of estimation is they are time efficient. In most of the studies carried out, the experimental unit/group is a litter. It has been observed that there is a tendency of littermates to respond more alike than animals from different litters, the “litter effect”. This litter effect is also known as the extra-dispersion (over/under- dispersion) or the intra-litter correlation. These litters may be of equal or unequal sizes. The concern here is with methods of establishing the confidence interval for the proportion of defective units p in unequal groups with adjustment for overdispersion using bootstrap technique.
Overdispersion is the phenomenon of having greater variability than predicted by the random component of the model; this is common in the modeling of binomial distribution for group testing [6] . Overdispersion is a very common feature in applied data analysis because naturally populations are frequently heterogeneous contrary to the assumptions implicit within widely used simple parametric models. The over-dispersion parameter is common in proportions in biology, toxicology, medicine, genetics and other similar fields and is important in making inference regarding the regression parameters on the mean [7] .
Maximum likelihood estimation gives a unified approach to estimation, which is well-defined, in binomial distribution and many other problems. The maximum likelihood as an estimator has been studied and seconded as an approach for using the proposed extended Beta-Binomial (BB) model to analyze over/under-dispersed proportions [8] . They estimated this parameter using maximum likelihood estimation (MLE). This concurred with the observation that the MLEs may be biased when the sample size n or the total Fisher information is small [9] . This bias is usually ignored in practice, the justification being that it is small compared with the standard errors.
Studies on point estimation in terms of bias and efficiency and the test for presence of overdispersion for both counts and proportions data have been done [10] . Interval estimation methods in which groups were of unequal sizes were carried out using interval based on the MLE, the Logit and CLL [11] . The quasi-likelihood approach to correct for overdispersion is used by [6] , he examines interval estimation methods based on functions of the MLE, the Logit and CLL functions.
2. Literature Review
2.1. Bootstrapping
The bootstrap method was introduced by [12] . It is a very general resampling procedure for estimating the distributions of statistics based on independent observations. It has spread fast in statistical sciences within the last decades. The primary task of a statistician is to summarize a sample based study and generalize the finding to the parent population in a scientific manner. Of course, a summary statistic like the sample mean will fluctuate from sample to sample and a statistician would like to know the magnitude of these fluctuations around the corresponding population parameter.
To understand bootstrap, suppose it were possible to draw repeated samples (of the same size) from the population of interest, a large number of times. Then, one would get a fairly good idea about the sampling distribution of a particular statistic from the collection of its values arising from these repeated samples. But, that does not make sense as it would be too expensive and defeat the purpose of a sample study. The purpose of a sample study is to gather information cheaply in a timely fashion. The idea behind bootstrap is to use the data of a sample study at hand as a “surrogate population”, for the purpose of approximating the sampling distribution of a statistic, that is, to resample (with replacement) from the sample data at hand and create a large number of “phantom samples” known as bootstrap samples. These samples can be used to obtain more improved estimation of unknown parameter (s) of a probability model.
Recently, study has been done on the construction of bootstrap confidence intervals for the overdispersion parameter in equal proportions in Beta Binomial using Maximum Likelihood Estimator, Method of Moments Estimator and Quasi-likelihood [13] . Bootstrapping has been seen to provide improved CIs and is useful even when very little is known about the underlying distributions [14] .
2.2. Estimation of Proportions
2.2.1. Confidence Intervals Based on the Maximum Quasi-Likelihood Estimate
Overdispersion causes one to underestimate the variance of parameter estimates. A quasi-likelihood approach can be employed to correct for the overdispersion phenomenon which occurs with binary data [15] . For binary data, an alternative method for handling overdispersion is to use models for which a binomial parameter itself has a beta distribution [16] . However, the MLE of the beta-binomial method has been shown to be less flexible than that of the quasi-likelihood approach, and so cannot be recommended for general use. For comparisons of CI methods in previous literature, the overdispersion phenomenon needs to be taken into account for constructing the CI of the proportion. Therefore, the objective is to use quasi-likelihood methodology to evaluate several asymptotic CI methods and construct bootstrap CI based on these methods for groups of different sizes, adjusted for overdispersion in group testing.
Suppose for 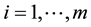 and
and 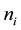 groups of size
groups of size , are tested, and
, are tested, and  of these groups test positive. The binomial parameter for the distribution of
of these groups test positive. The binomial parameter for the distribution of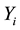 , which is the probability the groups tests positive is,
, which is the probability the groups tests positive is, 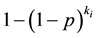 , where p is the probability an individual unit tests positive. Therefore considering overdispersion, the expected value and the variance of
, where p is the probability an individual unit tests positive. Therefore considering overdispersion, the expected value and the variance of 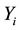 are
are
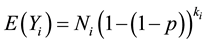 (1)
(1)
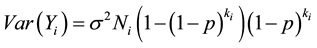 (2)
(2)
When groups of unequal size occur and overdispersion occurs together, the variance of the quasi-score function of p is
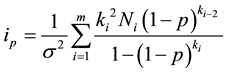 (3)
(3)
The maximum quasi-likelihood estimate of p denoted as , is the solution to
, is the solution to
 (4)
(4)
where
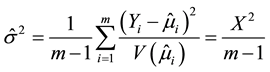 (5)
(5)
And
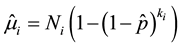 (6)
(6)
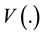 is a variance function, and
is a variance function, and 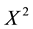 is the generalized Pearson statistic.
is the generalized Pearson statistic.
Under the usual limiting conditions on the


Then the 
where 

2.2.2. Confidence Intervals Based on the Logit
Asymptotic-likelihood methods to construct the 

Let 


tiable, then the information that Y contains about 
For the logit transformation


Thus the information of logit (p) is

After adjusting for overdispersion, the 

where

2.2.3. Confidence Intervals Based on the Complementary Log Log (CLL)
Hepworth also presented the CLL parameter transformations.
Suppose

And

The information of 

Then the 

where 
2.3. Choice of Group Sizes
A lot of attention has been devoted in studies to problems involving the group sizes, k. The question being what values should be chosen for k, the number of units in each group. If k is too large, π is close to 1 and all groups are likely to test positive, also if k is too small, π is closer to 0 [17] . When k is large group testing becomes uninformative and expensive. Therefore it is suitable to choose group sizes that produce some positives and some negatives. We therefore ensured that the sample sizes used yielded the desirable level, that is, margin of error is minimized.
2.4. Interval Width and Coverage Probability
Each Interval was examined for its Interval width and coverage probability. Confidence Intervals based on MLE ordering and Sterne’s technique for a dilution assay with 64 outcomes was compared [18] , those with the shorter widths were considered superior. The width of the intervals is considered an important criterion in comparing CI methods. Interval widths of the intervals were examined since the three methods; Wald, Logit and CLL do not differ a great deal with respect to coverage.
Coverage probability gives the proportion of the time that the interval contains p. Bootstrapping enabled us to estimate the coverage of the CIs with respect to the number of hypothetical repetitions of the entire procedure. The nominal coverage will be set at 0.95. The actual coverage of the three methods will be compared to the nominal coverage, greater coverage than the nominal is preferable and hence conservative.
3. Simulation
First, positive groups, 



The nominal coverage probability is set at 0.95.
This is then compared to estimating p from the same data that is the Yi’s without bootstrapping and the program run repetitively so as to calculate the coverage probability.
The number of bootstraps B’s were varied for the same combination of p, 

Next p was varied for the same Ni, ki and the same number of bootstrap simulations (500), and coverage probabilities are obtained.
Lastly, interval widths for the data are calculated for bootstrapping technique for the three interval methods and compared to those intervals got from each of the three methods without bootstrapping. This is in order to investigate whether bootstrapping gives more precise intervals.
4. Discussion
Group testing was primarily used to inspect individual members from a large population [1] . Therefore probability used in this study ranged from 0.01 to 0.2. From Table 1 it was seen that the CLL and the Logit gave more conservative coverage probabilities consistently for different bootstrap simulations for p = 0.02. All the three methods differ only slightly with CLL and Logit sometimes taking the same values of coverage probability. The coverage probabilities oscillate about the nominal level with Wald being less conservative than CLL and Logit. This was then compared to coverage probabilities of the three methods for the same data combination without applying bootstrapping technique. Similarly CLL outperformed the Wald interval method and at times the Logit Interval method as seen in Table 2. It is clearly seen that without bootstrapping technique, CIs generated have lower coverage probabilities than CIs generated after applying bootstrapping.
In Table 3 and Figure 1, the number of bootstrap simulations was varied. It was seen that as the number of
Table 1. Coverage probabilities for the three Interval methods for 500 simulations for p = 0.02.
Table 2. Coverage probabilities for data for 500 simulations without bootstrapping for p = 0.02.
Table 3. Coverage probabilities for the three methods for varying bootstrap simulations (B) for p = 0.02.
Figure 1. The figure shows a plot of coverage probabilities for the three methods for varying bootstrap simulations for p = 0.02 and for a nominal coverage probability of 0.95.
bootstrap simulations increased, all the three methods became more precise, that is, their coverage probabilities hovered slightly above and below the nominal coverage probability.
Group testing works best when the prevalence rate or the proportion is sufficiently small. According to Table 4 and Figure 2, we see that as the proportion increases to 0.1 the coverage probability becomes very low for all the three interval methods. Between 0.03 and 0.08, the coverage probabilities for the three methods are conservative.
From Table 5 and Table 6, it is seen that the interval widths for both CLL and Logit are not differing a great deal for the same bootstrap simulations. CLL has shorter widths than logit. However, interval widths for the Wald for the three bootstrap simulations are considerably wider than those of the other two interval methods. When interval widths are compared without bootstrap simulations to those interval widths with bootstrap simulations we note that they are wider.
According to Table 4 and Figure 2, all the three methods perform well as the number of bootstrap simulations increases, with the coverage probabilities of the CLL and Logit being oftentimes greater than the nominal coverage probability.
Figure 2. The figure above is a plot of coverage probabilities for the three methods for 500 bootstrap simulations for varying probability, that is, 0.01 < p < 0.2.
Table 4. Coverage probabilities for varying p for the same 500 simulations for a nominal coverage of 0.95.
Table 5. Table of interval widths for the three interval methods for data without bootstrapping.
Table 6. Table of interval widths for the three interval methods after bootstrapping.
5. Conclusion
Bootstrap methods produce good confidence intervals by an order of magnitude upon the accuracy of standard intervals [19] . In this paper we implement bootstrapping to the three interval methods: Wald, CLL and Logit. The comparison results in this study show that bootstrapping produces more precise confidence intervals than standard intervals for all the three procedures. Likewise the coverage probabilities from the three methods are consistent with the CLL being most conservative. Wald is more liberal. As the number of bootstrap simulations increases the more conservative the coverage becomes.
Cite this paper
Olivia WanjeriMwangi,AliIslam,OrawoLuke, (2015) Bootstrap Confidence Intervals for Bootstrap Confidence Intervals for Adjusted for Overdispersion. Open Journal of Statistics,05,502-510. doi: 10.4236/ojs.2015.56052
References
- 1. Dorfman, R. (1943) The Detection of Defective Members of Large Populations. The Annals of Mathematical Statistics, 14, 436-440.
http://dx.doi.org/10.1214/aoms/1177731363 - 2. Fletcher, J., Russell, A. and Butler, R. (1999) Seed-Borne Cucumber Mosaic Virus in New Zealand Lentil Crops: Yield Effects and Disease Incidence. New Zealand Journal of Crop and Horticulture Science, 27, 197-204.
http://dx.doi.org/10.1080/01140671.1999.9514097 - 3. Worlund, D. and Taylor, G. (1983) Estimation of Disease Incidence in Fish Populations. Canadian Journal of Fisheries and Aquatic Science, 40, 2194-2197.
http://dx.doi.org/10.1139/f83-254 - 4. Swallow, W.H. (1985) Group Testing for Estimating Infection Rates and Probabilities of Disease Transmission. Phytopathology, 75, 882-889.
http://dx.doi.org/10.1094/phyto-75-882 - 5. Kline, R.L., Bothus, T., Brookmeyer, R., Zeyer, S. and Quinn, T. (1989) Evaluation of Human Immunodeficiency Virus Seroprevalence in Population Surveys Using Pooled Sera. Journal of Clinical Microbiology, 27, 1449-1452.
- 6. Liu, S.-C., Chiang, K.-S., Lin, C.-H. and Deng, T.-C. (2010) Confidence Interval Procedures for Proportions Estimated by Group Testing with Groups of Unequal Size Adjusted for Overdispersion. Journal of Applied Statistics, 38, 1467-1482.
http://dx.doi.org/10.1080/02664763.2010.505953 - 7. Paul, S. and Islam, A.S. (1998) Joint Estimation of the Mean and Dispersion Parameters in the Analysis of Proportions: A Comparison of Efficiency and Bias. Canadian Journal of Statistics, 26, 83-94.
http://dx.doi.org/10.2307/3315675 - 8. Saha, K.K. and Paul, S.R. (2005) Bias-Corrected Maximum Likelihood Estimator of the Negative Binomial Dispersion Parameter. Biometrics, 61, 179-185.
http://dx.doi.org/10.1111/j.0006-341X.2005.030833.x - 9. Williams, D.A. (1975) The Analysis of Binary Responses for Toxicological Experiments Involving Reproduction and Teratogenicity. Biometrics, 31, 946-952.
http://dx.doi.org/10.2307/2529820 - 10. Saha, K.K. (2008) Semi-Parametric Estimation for the Dispersion Parameter in the Analysis of over- or Underdispersed Count Data. Journal of Applied Statistics, 35, 1383-1397.
http://dx.doi.org/10.1080/02664760802382459 - 11. Hepworth, G. (2005) Confidence Intervals for Proportions Estimated by Group Testing with Groups of Unequal Size. Journal of Agricultural, Biological, and Environmental Statistics, 10, 478-497.
http://dx.doi.org/10.1198/108571105X81698 - 12. Efron, B. (1979) Bootstrap Methods: Another Look at the Jackknife. The Annals of Statistics, 7, 1-26.
http://dx.doi.org/10.1214/aos/1176344552 - 13. Siele, D. (2012) Interval Estimation for the Beta Binomial Dispersion Parameter. MSc Thesis, Egerton University, Njoro.
- 14. Saha, K. and Sen, D. (2009) Improved Confidence Interval for the Dispersion Parameter in Count Data Using Profile Likelihood. Technical Report No. 4/09.
- 15. Williams, D.A. (1982) Extra-Binomial Variation in Logistic Linear Models. Journal of the Royal Statistical Society. Series C (Applied Statistics), 31, 144-148.
http://dx.doi.org/10.2307/2347977 - 16. Crowder, M.J. (1978) Beta-Binomial Anova for Proportions. Applied Statistics, 27, 34-37. Mathematical Statistics, 14, 436-440.
- 17. Hepworth, G. (1996) Exact Confidence Intervals for Proportions Estimated by Group Testing. Biometrics, 52, 1134-1146.
http://dx.doi.org/10.2307/2533075 - 18. Loyer, M.W. and Hamilton, M.A. (1984) Interval Estimation of the Density of Organisms Using a Serial-Dilution Experiment. Biometrics, 40, 907-916.
http://dx.doi.org/10.2307/2531142 - 19. Efron, B. and DiCiccio, T. (1996) Bootstrap Confidence Intervals. Statistical Science, 11, 189-228.
http://dx.doi.org/10.1214/ss/1032280214






