Received 8 April 2015; accepted 2 August 2015; published 5 August 2015

ABSTRACT

In light of rapid development of customer requirements, control procedures of quality concept use multivariate analysis. This is because of recent advances in information technology and in recording. The charting procedures are based on Mahalanobis distance but their performance needs normality and a type-I error rate choice. The DD-diagram is an alternative scheme that uses data depth to avoid these conditions rarely met in practice. For a given error-free sample, the performance of DD-diagram and that of multivariate EWMA control procedures are compared through a real example on individual observations taken from a multivariate quality process.

Keywords:

Multivariate Data, Quality Control, Mahalanobis Distance, MEWMA Chart, Data Depth, DD-Diagram

1. Introduction

Multivariate control schemes are valuable when several process features are being observed to identify instability within the manufacturing quality process that exhibits substantial cross-correlations. These control schemes use relationships between quality characteristics to generate powerful control procedures that are sensitive to shifts in position and/or in dispersion.

Multivariate Shewhart control chart was first introduced in 1947 and it is known as Hotelling’s 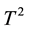chart. Then, a number of multivariate control charts were designed to suit different situations such as multivariate EWMA charts and multivariate CUSUM charts. These classical monitoring charts have been developed to monitor the mean vector of quality characteristics under a number of assumptions quoted by [1] . The perfor- mance of these multivariate control charts relies heavily on the hypothesis that the underlying distribution of the quality process is multivariate normal which in practice rarely holds. To overcome this limit, a DD-diagram, suggested by [2] and discussed by [3] , is a visual procedure designed as an alternative tool. It is based on a centre-outward ranking which uses data depth plot to monitor any multivariate quality data and does not require any assumptions about the underlying distribution of the process. For a given error-free sample, the DD-diagram is used to signal out any point of another observed sample taken from a multivariate quality process. This new scheme based on data depth uses a properly chosen limiting variation line or L-value in order to evaluate the outlyingness of every point in the observed sample in all directions of the considered p-variates of quality process.

In this paper, an application of both MEWMA control chart and DD-diagram is conducted using individual observations taken off a real case of quality process from the industry. The data of the samples are collected during two different times of the production process. The reference sample measures are drawn from a production process during which the process is considered in control. However, the empirical sample measures are drawn later in the frame work of a quality control routine. The MEWMA control chart and the DD-diagram are given in Sections 2 and 3, respectively. In Section 4 these monitoring techniques are applied. The empirical analysis is given in Section 5 and after that we dedicate Section 6 to draw some conclusions.

2. The Multivariate EWMA Control Chart

As the number of process variables grows the traditional multivariate control charts such as the 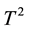control chart lose efficiency with respect to shift in position and/or in dispersion. The 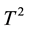chart is poor at detecting small and moderate shifts. However, the MEWMA control chart is known to respond quickly to small shifts and it includes the 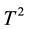scheme when the magnitude of its smoothing parameter goes to one, see the discussion of [4] .

Let be the quality of an item X at time period i, so if this level of quality is characterized by p-quality

characteristics 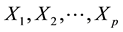then 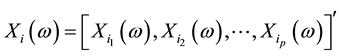or simply

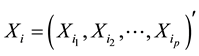(1)

is a vector-valued output at time. The components of the sample 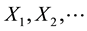are assumed to be in- dependent and identically distributed multivariate normal random variables with mean vector

and covariance matrix.

As indicated by [5] , there is no reason to weight past observations differently for the p-quality characteristics being monitored. So, the EWMA vector is the statistic

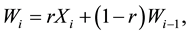(2)

where 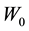is the p-dimensional null vector and r is a parameter, 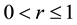, that specifies the magnitude of the smoothing. The multivariate EWMA chart indicates an out-of-control signal if the quantity

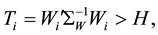(3)

where is chosen to achieve a specified in-control ARL. In order to calculate, the asymptotic form of the covariance matrix of is used,

(4)

The statistic is the Mahalanobis distance of the vector from the null vector. When the mean vector and the covariance matrix are known, the control chart for the’s series is constructed using the statistic in Equation (3). In reality, however, the parameters and are rarely known so they have to be estimated from a base period of n observations when the process is in-control. If the base period sample referred to as a reference sample of size n is denoted by, then the mean vector is estimated by such that

(5)

and the covariance matrix is estimated by

(6)

Replacing by its estimator of Equation (6), the empirical version of the statistic in Equation (3) takes the form of

(7)

such that

(8)

3. The DD-Diagram

Let F be a probability distribution in,. Throughout the following, unless stated otherwise, we assume that F is absolutely continuous and also that the reference sample is derived from F.

Therefore, if the quality of the observed unit is denoted by, then.

According to [6] , a data depth is a way of measuring how deep or central a given point is with respect to F or w.r.t. a given data cloud. Then using the statistical distance

(9)

the Mahalanobis depth at x with respect to F is defined to be

(10)

The sample version of Equation (10) is obtained by replacing and with their respective sample estimates in Equations (5) and (6), then

(11)

Henceforth, D or will be used to indicate the datum depth notion and a larger value of always implies a deeper (or more central) x with respect to F.

Given a notion of data depth, one can compute the depths of all quality measures and order them according to decreasing depth values. This gives a ranking of the sample point associated with the highest depth value. We view as the order statistics, with being the deepest or the most central point or simply the centre, and the most outlying point. The implication is that a larger rank is associated with a more outlying position with respect to the data cloud. These order statistics induced by a data depth are different from the usual order statistics on the real line, since the latter are ordered from the smallest sample point to the largest, while the former start from the middle sample point and move outwards in all directions, see [7] .

Given the definitions (10) or (11), the sample becomes, there is a natural choice of location parameter for the observed distribution. Specifically, the centre is the most central point so

(12)

When the depth-equivalence class contains more than one point measure, , according to Liu et al. (99) the median or the centre is the average of the deepest points, so in this case

(13)

On this basis and using data depth, the Equations (12) and (13) fix out a centre or a multivariate median. Moreover, [2] stated that if Mahalanobis depth is used, the central point defined in Equations (12) and (13) turns out to be the mean of the observed data. This suggests concepts of location which are intermediate between the mean and the median.

A data depth plots is a graphical comparison between two multivariate distributions based on data depth. So in addition to the reference sample, let be another sample referred to as an empirical sample of distribution G characterizing the observed quality process. The reference sample X is taken when the production process is in control and the empirical sample Y is drawn when inspecting the process during another period of time later. The DD-diagram is obtained when plotting data depth values of a sample versus the other. Precisely, the DD-diagram is defined by

(14)

Since is a subset of, the resulting graph is one-dimensional curve in the plane. If the two distributions are identical, the DD-diagram in (14) turns out to be the diagonal line from the point (0, 0) to (1, 1). Different patterns of deviations from the diagonal line in the DD-diagram are indications of differences in specific characteristics of F and G.

In general, the distributions are rarely known so instead we use an empirical version of the DD-diagram. If F and G are unknown distributions for the samples X and Y, then the DD-diagram is obtained when plotting

(15)

if Equation (11) is used to compute the data depth.

If and if F and G are both absolutely continuous, then DD-diagram corresponds to a region with non zero area. The area of this region can serve as a measure of the discrepancy between F and G, see [2] . If the two distributions are identical, the data cloud of the DD-plot should be concentrated along the diagonal line. Other patterns are indications of differences in specific characteristics of F and G i.e. in position, in scale, in skewness, ....

In most cases, the departure from the diagonal line usually takes the form of pulling down from the point to the origin, leaving the upper right corner empty and spreading out the points as a scatter plot diagram pointing at. In order to bring out scale differences, the centre of the samples should be equalized first by subtracting the obtained centre of Equation (12) or Equation (13) from the data points. Suppose that G is more spread out than the reference sample F, then the points in DD-diagram tend to arch toward the F sample around the origin.

In analogous manner to the classical multivariate control procedures, [8] has suggested upper and lower control limits in order to detect visually the shifts in location and/or in dispersion. The region under control is located between these two limits. This marked region turns out to be so large. In order to make the DD-diagram more sensitive, [9] has revised his study and proposed in instead a L-value as a least critical value for a data depth according to which the corresponding point will be considered to have components not satisfying the variation intervals,

(16)

It is conversely proportional to the sum of the depth of the reference sample centre, , and the Log function of modified degrees of freedom of the empirical sample, , minus the depth of the closest point to the centre, 1, all multiplied by with p being the number of the considered variables affecting quality. The role of this limiting value line is to decide graphically if the production process is in control or not. Therefore, if a point computed using (14) or (15) is lower than this, the observed process is out of control and an investigation must be made in order to point out which characteristic is responsible among the considered p-variates.

4. Application of MEWMA Chart and DD-Diagram

In this section individual observations data are collected from a production process during which the process is considered in control. These observations are then used to estimate the parameters of the underlying distribution F of the considered process. Then, another series of individual observations are drawn when the distribution of the process has drifted to a distribution G. Both series of observations are used to construct and to argue the performance of the monitoring schemes the MEWMA chart and the DD-diagram. Based on a previous work of [9] , the observation involves the simultaneous measurement of five variables: (1) the weight, (2) the module, (3) the humidity rate, (4) the pulling resistance and (5) the density.

Processing the observed data begins with the start-up stage that consists of estimating the parameters of F, constructing the control limit of MEWMA chart and determining the centre of F as reference sample.

According to Equation (5), the vector of sample mean is

and to Equation (6), the sample covariance matrix is

To construct a multivariate EWMA control chart, [5] gave a limiting value that corresponds to quality variates. This value suits to the asymptotic form in Equation (4) or its estimated form of Equation (8). Moreover, it is known that the MEWMA control chart sensitivity for small shifts is largely affected by the smoothing parameter value r. For this purpose, two cases for the smoothing parameter are considered when and when. These special cases of the MEWMA control chart are important because they yield if leading to the statistic of the multivariate Shewhart control chart and if one includes the history of the process this requires that r moves away from 1 (i.e.) for which the MEWMA control chart is conceived.

Figure 1 shows the corresponding MEWMA chart if and if (or multivariate Shewhart chart) for the reference sample. The observations were examined individually to determine a possible assignable cause and no observation is detected lying outside the in-control region specified by the above computed control limit.

To determine the centre, data depths of all observations of the reference sample are calculated using Equation (11). As recorded in the work of [9] , the highest value of the statistic data depth is for a sample of size. It corresponds to observation in the sample F so the most central point is defining a depth-equivalence class of order one containing a single cigarette with rank 45.

In order to detect graphically any point that is not satisfying the limiting variation interval, the for the minimum data depths is calculated according to Equation (16)

as the least acceptable data depth value and below which the corresponding point is considered out of control i.e. at least one of the p-characteristics exceeds its limiting variation interval.

It is clear that in the reference sample, the point of order 45 is characterized by the maximum data depth in either case before and after centering with respect to the computed vector-valued centre. This deepest point in the reference sample is marked by a circle in Figure 2.

5. Empirical Analysis

The second stage consists of using both control schemes to evaluate the stability of the observed production process when an empirical sample is drawn. At this phase, the parameters of the reference sample F obtained in

the start-up stage are used to monitor any taken empirical sample in the future. Specifically, after drawing the empirical sample G given in [9] the vector-valued mean and the covariance matrix S are used to assess the charting statistic and to construct the MEWMA chart if the smoothing parameter and.

Figure 3 shows the corresponding multivariate EWMA control chart for both cases and. Observations 19, 33, 50, 52 and 54 of the empirical sample lie outside the in-control region when whereas observations of order 3, 12, 13, 19, 29, 33, 34, 39, 43, 50, 51, 52, 53 and 57 when are detected out-of-control. These points are examined thoroughly to determine which characteristics are causing this drift in quality. Henceforth, we consider only the special case when because the other special case, when, was investigated by [9] .

Hereafter, the vector-valued centre and the limiting variation value are used to evaluate the data depths of all measures making up the G sample and also to identify any change in location and/or in scale of the process.

Figure 4 shows the corresponding DD-diagram for both cases before and after centering measures. Both subplots (left and right) of Figure 4 sketch out any change in location and/or a scale increase when moving from the distribution F to the distribution G in the multivariate quality process. The out-of-control observations in

Table 1 are indicated with red stars in both subplots of Figure 4 in the DD-diagram. In order to determine the characteristics responsible for this drift, refer to Table 1.

The first line of Table 1 gives the specification interval for each considered variable. Reading the corresponding values one by one indicates that cigarettes 19 and 54 are considered out of control because the “module” (X₂) exceeds its specified measure. The other observations (2, 3, 27, 29, 33, 39, 43, 50 and 52) are considered out of control because the humidity rate (X₃) is lower than its minimum value.

For centered measures, the DD-diagram in the right subplot of Figure 4 shows the observations under the effect of a scale change only. It can be deduced that observations 3 and 50 are out of control because of a change in location only. When measures are centered, these two observations disappear from the out-of-control region in the right subplot of Figure 4. But, observations 2, 19, 27, 29, 33, 39, 43, 52 and 54 are out-of-control under the effect of a change in dispersion and of a location shift respectively. These points are indicated with red stars in the DD-diagr am in the right subplot of Figure 4.

The MEWMA control chart, for, gives a larger set of out-of-control observations than the DD- diagram, not only the points 2, 3, 19, 27, 29, 33, 39, 43, 52 and 54, but also 12, 13, 34, 51, 53 and 57 of the empirical sample G. These points are signaled out-of-control because of a change in location and/or in scale respectively. They are indicated with red circles and numbers in Figure 3 in the MEWMA control chart. In order to determine the characteristics responsible for this drift, refer to Table 2.

Comparing the realized values for the out-of-control observations with respect to their specification intervals indicated in the first line of Table 2 indicates that cigarettes 12 and 19 are considered out of control because the “module” exceeds its specified measure. The other observations (3, 29, 33, 39, 43, 50, 51, 52 and 57) are considered out of control because the humidity rate is lower than its minimum value.

The investigation of Table 2 shows that there are 5 points fall out of control limit of the MEWMA chart which ar not detected by the DD-diagram. This means that the DD-diagram performs poorly with respect to the MEWMA chart. But if the coordinates of these points are revised with respect to their specification intervals they convey that they are not out of control limit in reality they are false alarms, such that observations 13, 34 and 53.

The DD-diagram is a graphical comparison that exhibits location shifts and/or scale increase when moving from the distribution F of the reference sample to the distribution G of the empirical one. And to use this dia- gram, we do not need any requirement about the nature of the observed multivariate quality process distribution. Although, this procedure looks like a non parametric method, DD-diagram does not require large samples. It suffices to have a size of the samples that goes beyond 30 to ensure a reasonable performance. So, whenever this size goes bigger the DD-diagram improves in performance.

6. Conclusions

The above application allows us to say that DD-diagram performs as better as multivariate EWMA control chart because its use does not depend on normality as for the case of MEWMA control chart. In the above application, DD-diagram detects 11 points indicating that their components exceed their specified limits whereas the MEWMA control chart gives 14 points corresponding to a smoothing parameter, among which false alarms. So decreasing the smoothing parameter r increases the performance of the MEWMA procedure but also false alarms.

When a multivariate quality process changes its distribution from F to G and if the location shift is eliminated i.e. centering the measures with respect to the centre or the deepest point of F, DD-diagram makes it possible to distinguish between the out-of-control observations that were drifted because of location shifts and scale increase respectively and those that were drifted under the effect of variations in dispersion only. This fact is not feasible when using MEWMA control chart.

In general consider the test of a null hypothesis asserting stability of a production process versus an alter- native one that concerns the existence of shifts in location and/or in scale, then the empirical sample has higher dispersion than that of the reference one. This is deduced from the fact that the resulting clouds, of centered measures or not, are located under the limiting variation level line at. Then DD-diagram enables to pre- sent and detect graphically any out-of-control observation that the components exceed their specified limits. In addition, the DD-diagram sends out an out-of-control signal when the outlyingness of a point exceeds a specified value in all directions.

Cite this paper

MekkiHajlaoui, (2015) On the Charting Procedures: MEWMA Chart and DD-Diagram. Open Journal of Statistics,05,373-381. doi: 10.4236/ojs.2015.55039

References