Received 9 March 2015; accepted 16 April 2015; published 20 April 2015

ABSTRACT

In clinical trials, drug effect is measured by a difference between subjects who are treated by experimental drug against placebo-treated subjects. In case of binary data, with observing YES/NO on each subject in certain period of time, it is the proportion of subjects who respond in treatment group minus the proportion of responders in placebo group (for example, 50% vs. 30%). However, a greater difference was proposed by Rihmer et al. (2011) [1] with their supporting arguments, in that antidepressant response and placebo response had different mechanisms and there were equal chances for antidepressant responder to be responding to placebo and not responding to placebo at all. Therefore, the authors proposed 50% - 30% * 50% when the response rate in the treatment group and the placebo group are 50% and 30% respectively, resulting in higher drug-placebo difference than traditional understanding of 50% - 30%. In this article, we tried to explain why the authors misunderstood the drug-placebo concept for evaluating drug superiority, their misunderstanding of assumptions of traditional calculation, as well as their wrong reasoning on their proposed approach. All in all, we conclude the traditional approach of 50% - 30% is the right way of evaluating drug-placebo difference and the possible methods to control impact of placebo effect are briefly discussed at the end of this article.

Keywords:

Antidepressant, Placebo Effect, Short-Term Antidepressant Effect, Unipolar Major Depression

1. Introduction

In clinical trials, patients are not only taking a testing drug on rigorous schedules, but also under a specific healthcare environment. Routine checks, clinical visiting and lots of psychological interviews might create a misconception to patients and clinicians and result in placebo effect. Placebo effect blunts the ability to detect drug-placebo difference in a well-controlled trail, resulting in trial failures, longer time and more resource in developing promising drugs for unmet medical needs. To deduce this trial background effects, randomization is normally applied. Subjects are randomized into either placebo or treatment group with equal probability and baseline characteristics got balanced out. With the help of randomization, only post-randomization factors and drug-placebo difference can contribute to different effects between drug and placebo groups. However, if investigators and patients have known what is given and what is taken in the trial, psychological effects will impact clinical rating scales, self-evaluation scores, compliance and patient’s willingness of coordination with trial personnel. Hence blinding is essential to get rid of above impacts on evaluating drug-placebo effect. Double- blinding is a way to exclude some of those post-randomization factors. Use of placebo is to evaluate the background effect of trial procedure on patients. Placebo is sometimes better than not treated, which is seen in most psychiatry trials depending on different disease characteristics. Placebo effect is well-known in antidepressant trials. How placebo works, how placebo effect is different from drug effect, whether there are interactions between them or not, and how these issues get accounted in statistical comparison all become interesting to the academic community. And the newly proposed method on how to calculate drug-placebo difference was one particular effort to answer one aspect of these questions. What makes anti-depressant special is that general antidepressant clinical trials, especially in short-term trials, have relatively larger placebo effect than those of other drug-testing clinical trials. Section 2 describes complexity of placebo and antidepressant mechanisms in depressive patients. Section 3 evaluates drug-placebo difference under various interaction types between placebo and antidepressant responses. Section 4 explains all the misunderstanding of drug-placebo difference and logic errors in Rihmer et al. 2011 [1] , similar errors were also made in other two articles (Rihmer, 2007 [2] ; Rihmer and Gonda, 2008 [3] ). Section 5 discusses operational management and novel designs to cope with placebo effect in antidepressant clinical trials.

2. Mechanisms of Placebo and Antidepressant Effects

Most widely used antidepressants include two classes: SSRI (selective serotonin reuptake inhibitors) and serotonin norepinephrine reuptake inhibitors. Namely, these two classes work mostly on central serotonin and norepinephrine systems (Johnson et al., 1993 [4] ); Carpenter et al., 2003 [5] ) respectively. That is: the AD (antidepressant) response relies on specific underlying biological pathway in relation to biological state/illness characteristics. Moreover, due to biochemical heterogeneity, depression symptomatic improvement only occurs in certain subpopulation of individuals affected by depression. Interestingly, PL (placebo) response behaves very differently, especially from perspective of its biomarker profile. When the biomarker of change in brain glucose metabolism, a measure of positron emission tomography was monitored, PL response was shown to be associated with regional metabolic increases in the prefrontal and anterior cingulate cortices, while fluoxetine (one kind of antidepressant) response was associated with additional changes in additional changes in brainstem, striatum, and hippocampal activity (Mayberg et al., 2002 [6] ). At subject level, PL (placebo) responders showed a significance increase in prefrontal cortex activity, whereas no such increase occurred in none of the rest of the population consisting of PL non-responders, AD (i.e. fluoxetine or venlafaxine) responders, and AD non-res- ponders (Leuchter et al., 2002 [7] ). Moreover, most recent studies showed endogenous opiod and dopaminergic neurotransmission mediated nocebo effects, while central opioid and dopaminergic activation mediated on PL response (Enck et al., 2008 [8] ); Scott et al., 2008 [9] ). Then next question is how the central opoid and dopaminergic activation differs from endogenous opiod and dopaminergic neurotransmission; recent research argued that the former could mediate optimistic personality features (Sharot et al., 2007 [10] ). Now the connection appears explainable, as placebo response, not with specific drug molecule, shows general response to the overall environment. For instance, some reward expectations on clinical improvement in both patients and clinicians after placebo administration, subsequently result in change in systems that mediate optimistic personality feature. So far, we can summarize that AD response and PL response work differently and could overlap in certain ways. Not everyone responds to placebo, neither does to antidepressants. From each subject, as Rihmer et al. (2011) [1] noted patients could be divided into four different categories: (P1) AD responder and PL responder (++); (P2) AD responder and PL non-responder (+−); (P3) AD non-responder and PL responder (−+); and (P4) AD non- responder and PL non-responder (−−). All types of P1 - P4 exist in real trial results.

3. Drug-Placebo Difference Evaluation

In this section, we would like to explore the appropriate statistical evaluation for drug-placebo difference under the circumstance of placebo response in antidepressant trials. To be more complete, let’s put aside all founding in Section 2 first and explore all the scenarios, because some of these scenarios trigger Rihmer and co-authors [1] to pick up the new method over the traditional one. Therefore, it is necessary to explore all of them in detail first.

Put AD and PL response in 2X2 contingency table, then the difference between drug and placebo can be viewed marginally and jointly. Marginally means whenever we consider AD response rate, we only concentrate on AD response (response = YES and response = NO corresponding to AD = 1 and AD = 0 respectively) without considering PL mechanism. Similarly, whenever looking at PL response rate, we ignore how AD works. From Figure 1(a), we can clearly see that rate of response in AD group minus rate of response in PL group is first column of down diagonal minus first row of up diagonal, that is Pr(AD = 1) − Pr(PL = 1) = 0.5 − 0.3. However, if we would like to look the rates jointly in terms of both AD and PL responding, then it is low left corner of down diagonal minus upper right corner of up diagonal, that is Pr(AD = 1 and PL = 0) − Pr(AD = 0 and PL = 1). Comparing to subtraction of marginal in method one in Figure 1(a), future specifications are needed to obtain these two joint probabilities of Pr(AD = 1 and PL = 0) − Pr (AD = 0 and PL = 1). Comparing method 1 of subtraction of marginal probabilities with subtraction of joint probabilities, we can find that they coincide with each other, since the only part in common, probability of being AD responder and PL responder, is eliminated from because residing both before the minus sign and after the minus sign. That is: Pr(AD = 1) − Pr(PL = 1) = [Pr(AD = 1 and PL = 0) + Pr(AD = 1 and PL = 1)] − [Pr(AD = 0 and PL = 1) + Pr(AD = 1 and PL = 1)] = Pr(AD = 1 and PL = 0) − Pr(AD = 0 and PL = 1). Note that, in Figure 2, we graphically denote divided probabilistic distribution of this joint AD and PL variables.

Assuming two difference systems mediate PL response and AD response separately, then these two systems could: (D) totally dependent; (IND) totally independent; and (Other) some dependence in between. For totally dependence, we can further divide them into 4 subcategories (Figure 3): (D1) all placebo responders are AD responders; (D2) all placebo responders are AD non-responders; (D3) all AD responders are placebo responders; (D4) all AD responders are placebo non-responders.

3.1. Various Dependent Structures

(D1): Dependence scenario 1. Since all PL responders are AD responders, Pr(AD = 1|PL = 1) = 1. Circled cell Pr(AD = 1 and PL = 1) = Pr(AD = 1|PL = 1) * Pr(PL = 1) = 1 * 0.3 = 0.3; and then drug-placebo difference = Pr(AD = 1 and PL = 0) − Pr(AD = 0 and PL = 1) = 0.2 − 0 = 0.2 = Pr(AD = 1) − Pr(PL = 1) = 0.5 − 0.3.

(D2): Dependence scenario 2. Since all PL responders are AD non-responders, Pr(AD = 0|PL = 1) = 1. Circled cell Pr(AD = 0 and PL = 1) = Pr(AD = 0|PL = 1) * Pr(PL = 1) = 1 * 0.3 = 0.3 and drug-placebo difference = Pr(AD = 1 and PL = 0) − Pr(AD = 0 and PL = 1) = 0.5 − 0.3 = Pr(AD = 1) − Pr(PL = 1) = 0.5 − 0.3.

(D3): Dependence scenario 3. Intuitively, this can’t exist because: if all AD responders are PL responders, PL responder rate will be greater or equal to AD responder rate, which contradicts our assumption of probability of AD equal to 1 being 0.5 and PL equal to 1 being 0.3 respectively. Had we have PL responder rate exceeded AD responder rate; this would be a wrong target drug to develop since its effect is numerically inferior to placebo. Mathematically, if we have all AD responders are PL responders, conditionally probability of Pr(PL = 1|AD = 1) = 1. Therefore, Pr(AD = 1 and PL = 1) = Pr(PL = 1|AD = 1) * Pr(AD = 1) = 1 * 0.5 > Pr(PL = 1) = 0.3. This violates probability axiom, as Pr(PL = 1) = Pr(AD = 1 and PL = 1) + Pr(AD = 0 and PL = 1) and should not be less than Pr(AD = 1 and PL = 1) alone. This calculation proves our intuitive interpretation: under the condition of all AD responders are PL responders, existing of AD non-responders being PL responders will lead to greater PL response rate than AD response rate, in which is against the goal of drug development.

(D4): Dependence scenario 4. Since all AD responders are PL non-responders, Pr(PL = 0|PL = 1) = 1. Circled cell Pr(PL = 0 and AD = 1) = Pr(PL = 0|AD = 1) * Pr(AD = 1) = 1 * 0.5 = 0.5 and drug-placebo difference = Pr(AD = 1 and PL = 0) − Pr(AD = 0 and PL = 0) = 0.5 − 0.3 = 0.2 = Pr(AD = 1) − Pr(PL = 1) = 0.5 − 0.3. Graphically, dependence scenario 2 equals dependence scenario 4. Let’s try to prove it mathematically.

Claim: D2 dependence structure is the same as D4 dependence structure.

Proof: D2 = >D4

Pr(AD = 1 and PL = 1) + Pr(AD = 1 and PL = 0) + Pr(AD = 0 and PL = 1) + Pr(AD = 0 and PL = 0) = 1

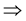Pr(AD = 1 and PL = 1) + Pr(PL = 0|AD = 1) * Pr(AD = 1) + Pr(AD = 0|PL = 1) * Pr(PL = 1) + Pr(AD = 0 and PL = 0) = 1

Because Pr(AD = 0|PL = 1) = 1, then Pr(PL = 0|AD = 1) * Pr(AD = 1) = 1 − 1 * Pr(PL = 1) − Pr(AD = 1 and PL = 1) − Pr(AD = 0 and PL = 0) = Pr(PL = 0) − Pr(AD = 1 and PL = 1) − Pr(AD = 0 and PL = 0)

= Pr(AD = 1 and PL = 0) − Pr(AD = 1 and PL = 1)

= Pr(AD = 1) * Pr(PL = 0|AD = 1) − Pr(AD = 1) * Pr(PL = 1|AD = 1)

After Canceling Pr(AD = 1) from both sides, we have Pr(PL = 0|AD = 1) = Pr(PL = 0|AD = 1) − Pr(PL = 1|AD = 1)

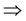Pr(PL = 1|AD = 1) = 0

Pr(PL = 1 and AD = 1) = 0

Together with Pr(PL = 0 and AD = 1) + Pr(PL = 1 and AD = 1) = Pr(AD = 1)

Pr(PL = 0 and AD = 1) = Pr(AD = 1)

Pr(PL = 0|AD = 1) * Pr(AD = 1) = Pr(AD = 1)

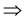Pr(PL = 0|AD = 1) = 1, because Pr(AD = 1) is a positive number.

Pr(PL = 0|AD = 1) = 1 is for D4 structure. All AD responders are PL non-responders.

Similarly, we can show D4 => D2.

In summary, under all reasonable dependence scenarios (i.e., D1 - D4 excluding D3), 4 cell probabilities are fixed and drug-placebo difference using joint probabilities is available. However, as discussed in Section 2, this drug-placebo difference is always 0.5 − 0.3, the same as that of being obtained by marginal probabilities. The other reason to have detailed discussion about above mutually exclusive and exhaustive scenarios is for later discussion about the method proposed by Rihmer et al. (2011) [1] .

3.2. Independent Structure

If the mechanism of placebo response is independent of that of antidepressant response, placebo responders can randomly either to be AD responder or to be AD non-responder. Similarly, AD responders have an equal chance to either be PL responder or be PL non-responder. Being a placebo responder is independent of being an AD responder. Then, under this scenario, what about drug-placebo difference? In Figure 4, we see that since Pr(AD = 1|PL = 1) = 0.5, we have Pr(AD = 1 and PL = 1) = Pr(AD = 1|PL = 1) * Pr(PL = 1) = 0.5 * 0.3 = 0.15. Then drug-placebo difference using joint probability is 0.35 − 0.15 = 0.2, numerically exactly the same as Pr(AD = 1) − Pr(PL = 1) = 0.5 − 0.3 = 0.2 using marginal probabilities.

3.3. Structures between Totally Dependent and Totally Independent

If neither definite dependence nor independence presents, some other structures in between play a role for mechanisms of placebo and AD responding. As in the 2X2 contingency table (Figure 2), once one cell probability is fixed, all other cells are known as well. For instance, probability of both AD and PL (i.e., Pr(AD = 1 and PL = 1)) responding is known. In example 1, with Pr(AD = 1 and PL = 1) = 0.25 known (bigger than the probability under independence in Figure 4), drug-placebo difference can be calculated as Pr(AD = 1 and PL = 0) = Pr(AD = 0 and PL = 1) = 0.25 − 0.05 = 0.2, the same as Pr(AD = 1) − Pr(PL = 1) = 0.5 − 0.3 = 0.2. In example 2, with Pr(AD = 1 and PL = 1) = 0.1 known (smaller than its probability under independence scenario), drug-placebo difference can be calculated as Pr(AD = 1 and PL = 0) = Pr(AD = 0 and PL = 1) = 0.4 − 0.2 = 0.2. As shown in Figure 5, Pr(AD = 1 and PL = 1) can be either greater than that of independence scenario in example 1, or less than that of example 2. No matter it is higher or lower than that of independence structure, once joint probabilities are known, drug-placebo difference can easily derived, which again is the same as the marginal probability difference. The advantage of using marginal probability is that joint probabilities are normally unknown due to unobservable property and can’t be used to derived drug-placebo difference. On the contrary, marginal probabilities are always observable and hence can easily be used for evaluating drug superiority.

In clinical trials, we measure response on each subject, and group them into treatment versus placebo to find a measure so that superiority of drug vs. placebo can be evaluated and tested. Each joint probability is actually unobservable in the trial except under wholly independence or dependence structures. It may be possible to use another trial to test independence assumption, but normally we can just reject or fail to reject independence hypothesis. Still, we can’t prove it is indeed independent. For dependence structure, even with an external trial specifically for evaluating dependence structure, it is really hard to prove which dependence structure it is. Also, from Section 2, the presence of AD non-responder and PL responders excludes the possibility of having dependence scenario 1, which is all PL responders are AD responders; similarly, the presence of AD responders and PL responders excludes dependence scenarios 2 and 4, which are all PL responders are AD non-responders and all AD responders are PL non-responders respectively.

From general discussion in Section 2 and each specific example in Section 3, we all show that drug-placebo difference can be evaluated by marginal probability difference.

4. Discussion of Misunderstanding Leading to a Wrong New Approach

After stating and proving the right way of evaluating drug-placebo difference, we now have to discuss why the proposed method by Rihmer et al. (2011) [1] is wrong and where the logic flaws resided in their article. There are several steps for Rihmer and co-authors [1] to propose 0.5 − 0.3 * 50% and reason against the traditional method of 0.5 − 0.3. First of all, they thought that old method of 0.5 − 0.3 depends on the assumption of all PL responders being AD responders (i.e., Pr(AD = 1|PL = 1) = 1), which corresponds to dependence structure 1 in Figure 3. This is indeed wrong. Under dependence structure 1, Then the authors had a wrong perspective that drug-placebo difference is Pr(AD = 1 and PL = 0) = Pr(AD = 1) − Pr(AD = 1 and PL = 1) = 0.5 − 0.3 using joint probabilities in Figure 3 Dependence 1 table. This is actually using a wrong rational but to end up with a correct number of 0.2. Later they thought that more consideration should be put into Pr(AD = 1 and PL = 1) to account for the fact that not all PL responders can be AD responders. Under independence structure, there is equal probability for a PL responder to be an AD responder or not to be an AD responder. Hence they went to independence structure in Figure 4. As joint probabilities in Figure 4 show, Pr(AD = 1 and PL = 0) = Pr(AD = 1) − Pr(AD = 1 and PL = 1) = 0.5 − 0.15 = 0.35.

We think that Rihmer and co-authors [1] started with wrong assumptions for drug-placebo difference; used wrong measure for it; had a wrong interpretation for this measure; and subsequently proposed a wrong approach. Now, let explain further about why probability of being an AD responder but not a PL responder (i.e., Pr(AD = 1 and PL = 0)) is not a right measure of drug-placebo difference. This measure is measuring the chance for each individual to be AD responder and PL non-responder simultaneously; or is measuring relative frequency of subjects who are AD responder but not PL responder in the whole population. Either interpretation has nothing to do with the drug-placebo difference, which is the relative frequency of AD responders over PL responders in antidepressant patient population. And this joint probability is normally unobservable in the clinical trials, where patients are randomly assigned to PL or AD to obtain efficacy measure to assess AD relative superiority. On the contrary, each patient is a unit to be treated by either placebo or AD; responder rate in AD-treated group minus the responder rate in the PL-treated group provide an objective measure for drug-placebo difference after all baseline factors being balanced out by randomization and the only factor contributing to drug-placebo difference is what they have received in the trial. This, as shown in Section 3, is irrespective of what kind of joint mechanism between drug and placebo responses. Besides, calculation from marginal rate difference is the same as calculating difference from joint probabilities, whereas the latter is normally unobservable and can’t be obtained from this randomized clinical trial.

5. Discussion of Operational Management and Novel Designs to Cope with Placebo Effect in Antidepressant Clinical Trials

After the discussion of the right way of understanding and evaluating drug-placebo difference and pointing out all the flaws in Rihmer and co-authors’ wrong proposal, it seems that we are going back to the original place to favor traditional method of Pr(AD = 1) − Pr(PL = 1). Then what should we do to avoid jeopardizing a trial because of placebo effect? And should we just let it go unchecked? Of course, the answer is no. This is actually a very interesting but complicated area and not intended to be covered in this article. Here, we can briefly point out some related perspectives. To avoid failure trial due to placebo effect, we can put more efforts on innovated design and manage it more appropriate in operation. The main challenge is to lower the optimistic expectation from both patient and clinician. Since higher placebo response was found in mild-moderate depression, excluding these patients in the trial should be considered. And more scientific scoring system, more self-scoring scale, help from biomarker markers, and/or central rating could be combined to narrow the possibility of overstated expectation. Mathematically, novel designs as sequential parallel designs are also available in the literature.

References