Received 14 September 2014; revised 12 October 2014; accepted 6 November 2014

ABSTRACT

In this work we introduce a Brownian motion in random environment which is a Brownian constructions by an exchangeable sequence based on Dirichlet processes samples. We next compute a stochastic calculus and an estimation of the parameters is computed in order to classify a functional data.

Keywords:

Bayesian Model, Brownian Motion, Exchangeability, Gaussian Mixtures

1. Introduction

The Brownian motion is a very interesting tool for both theoretical and applied math. Brownian motion is among the simplest of the continuous-time stochastic processes, and it is a limit of both simpler and more complicated stochastic processes. In this paper we construct a new process called Dirichlet brownian motion by the usual i.i.d. Gaussian sequence used in Brownian motion constructions is replaced by an exchangeable sequence.

Despite its recent introduction to the literature, hierarchical models with a Dirichlet prior, shortly Dirichlet hierarchical models, were used in probabilistic classification applied to various fields such as biology [1] , astronomy [2] or text mining [3] and finance [4] - [6] . Actually, these models can be seen as complex mixtures of real Gaussian distributions fitted to non-temporal data.

The aim of this paper is to extend these models and estimate their parameters in order to deal with temporal data following a stochastic differential equation (SDE).

The paper is organized as follows. In Section 2 we briefly recall Ferguson-Dirichlet process. In Section 3 we consider a different construction of the Brownian motion based on an exchangeable sequence from Dirichlet processes samples which is shown to be a limit of a random walk in Dirichlet random environment. In Section 4, we prove the regularity of the new process and in the Section 5 we give some stochastic calculus and an estimation of the parameters of DBM.

2. Ferguson-Dirichlet Process

Let 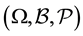be a fixed probability space. Let be a Polish space and let 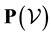denote the set of all probability measures defined on. The distribution of a random variable, say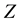, will be denoted by ethe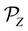r or.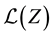

The following celebrated random distribution defined by Ferguson [7] plays a central role in our construction. Let 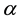be a finite positive measure on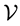. A random distribution is a Dirichlet process 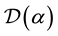if for every 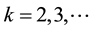and every measurable partition of, the joint distribution of the random vector has a Dirichlet distribution with parameters 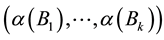Ferguson proved that this definition satisfies the Kolmogorov criteria which yields the existence of such random distributions.

For, let denote the Poisson-Dirichlet distribution with parameter (Kingman [8] ) which support is the set

Ferguson has also shown that for a.a., is a discrete probability measure: there exist an i.i.d. sequence of random variables on, say, and a sequence of random weights verifying:

(1)

such that

Let be a probability space on which are defined all the random variables (r.v.) mentioned in this

paper. The probability distribution of a r.v. will be denoted. Equality in distribution is denoted by.

For any integer, let denote the group of permutations of.

Exchangeable Random Variables

Definition 1 A sequence of r.v.s is said to be exchangeable if for all

(2)

Using transpositions, first notice that (2) implies that all the have the same distribution, say:

(3)

and also

(4)

The variables are assumed to take their values on a separable space and denote the separable set (for weak convergence topology) of all probability measures defined on.

An i.i.d. sequence is of course exchangeable but an exchangeable sequence needs neither be independent nor Markov.

For example a sequence of centered Gaussian variables with and is exchangeable but not i.i.d.

Another interesting example of exchangeable sequence is a sample from a Dirichlet process with precision parameter and mean parameter [7] :

The following celebrated theorem states that an exchangeable sequence is somewhat conditionally i.i.d. as in the preceding example. It was first established by de Finetti (1931) [9] in the case of Bernoulli variables and by Hewitt-Savage (1955) [10] in the general case. Very elegant proofs can be found in Meyer (1966) [11] p. 191- 192 and Kingmann (1978) [8] .

Theorem 1 (de Finetti-Hewitt-Savage) Let be an exchangeable sequence with values in. Then there exists a probability measure on such that

(5)

(6)

(7)

In other words, (5) shows that the distribution of an exchangeable sequence is a mixture with mixing measure, (6) shows that is the distribution of the weak limit empirical measure and finally (7) shows that if is considered as a parameter, then is a sufficient statistic for estimating.

Applying (5) with it is seen that the mean of, defined as, is equal to the common distribution of the:

(8)

In the example of a sample from the Dirichlet process, is nothing but the Dirichlet process itself, by definition of such a sample [7] , while

(9)

For the rest of the paper it is assumed that the real line.

3. DBM Constructions

3.1. DBM Based on Ciesielski Construction

We follow L. Gallardo [12] pp. 79-80 and 206-208.

Let

For any integer and let

that is,.

The functions and for and constitute what is called the Haar Hilbertian basis of.

Let

Note that is a nonnegative triangle function with support in so that

(10)

and

(11)

The functions and consitute the so called Schauder system.

Now, let be a an exchangeable sequence such that for one (and any).

Notice that (3) and (4) then imply that

(12)

are constants which do not depend on and.

Let

Then

Proposition 2 The series with general term converges in and

defines a stochastic process.

Proof: Due to (10) we have

and then (12) applied to the sequence and (11) give

Then and so that converges in. ■

Now, consider the following condition on the tails of:

There exists a convergent series with positive general term such that the series with general term

(13)

Proposition 3 If condition (13) holds then a.a. paths of are continuous.

Proof: Due to (10) and (11) we have

and (5) implies

the preceding inequality being due to the inequality for any which is a conse- quence of finite increments theorem.

Due to (13) we then get that the series with general term converges.

Then by Borel-Cantelli lemma, we have for a.a., for large enough so that the series converges uniformly and defines a continuous function of. Thus for a.a., is continuous. ■

As a corollary observe that

Proposition 4 For a sample of, a.a. paths of are continuous.

Proof: Condition (13) holds for with. Indeed, since

that is

holds for any positive number, we have for any

which is the general term of a convergent series. ■

3.2. DBM Based on Random Walks

Let and be fixed.

First, let be a sequence of random variables such that

which are more explicitly described by the following hierarchical model

(14)

We will rather consider centered variables

Now, consider the following random walk in Dirichlet random environment, starting from 0:

so that we have

It is straightforward that

Since the’s are independent with zero mean, we have

Therefore is finite a.e. or equivalently, for a.a.

(15)

For any integer and real number let

(16)

where denotes the integer part of.

Let denote a zero mean Brownian motion with variance, denoting the standard Brownian motion.

Proposition 5 For any, we have in the space of distributions

where is defined in (15).

3.3. DBM

A Brownian motion in Dirichlet random environment (BMDE) is a process such that

Proposition 6 If is BMDE then its conditional increments are independent Gaussians

The increments are orthogonal, are mixtures of Gaussians but need not be independent. Indeed, since

we see that

4. Regularity

Theorem 7 Let be as in (ref) then

so that there exist a continuous version of (Z_t)

Proof:

Since then

where Conditional to the, is a linear combina- tion of, then it is a gaussian random variable with 0 mean and variance

conditional to.

5. Simulation and Estimation

5.1. Sethuraman Stick-Breaking Construction

Sethuraman (1994) [13] has shown that the sequence of random distributions

(17)

converges to the Dirichlet process when the random weights are defined by the following stick-breaking construction:

(18)

(19)

5.2. Simulation Algorithm

A path of the BMDE process can be simulated as follows:

Let be small enough and let be the stick-breaking precision

Draw from (19)

Draw with

Compute by truncating (15)

Put and draw points such that

5.3. Estimation

Using proposition 6 we can show that

(20)

6. Stochastic Calculus

Consider the natural filtration defined by, that is the sigma algebra generated by A random process is a step process if there exist a finite sequence of numbers and square integrable random variables such that

(21)

where is -measurable for The set of random step processes will be denoted by Observe that the assumption that the are to be -measurable ensures that is adapted to the filtration The assumption that the are square integrable ensures that is square integrable for each The stochastic integral of is defined as

(22)

Proposition 8 For, we have and

where

This enables us to define with standard techniques, the stochastic integral

for any continuous function.

Proposition 9 The stochastic process is a -martingale

Proof:

Let and two reals numbers such that, let such that, let

where

since for every, and is -measurable then,

On the other hand for every using the zero means of increment conditional to.

consequently,

Itô Formulae

In this paragraph we shall give an expression of Itô formulae of the process

Proposition 10

Proof:

Since

Suppose that

For almost surely,

On the other hand for almost surely and for any

Therefore according to the dominus convergence theorem,

this means that

as required. ■

Proposition 11 Let f be a bounded and 2 times derivable function, then

7. Conclusion

We have extended Brownian motion in dirichlet random environment for the application on the Dirichlet hierarchical models in order to deal with temporal data such as solutions of SDE with stochastic drift and volatility. It can be thought that the process on which are based these parameters belongs to a certain well-known class of processes, such as continuous time Markov chains. Then, we think that a Dirichlet prior can be put on the path space, that is a functional space. It seems to us that the estimation procedure in such a context is an interesting topic for future works.

References