Open Journal of Statistics
Vol.04 No.10(2014), Article ID:51471,10 pages
10.4236/ojs.2014.410078
Parallel and Hierarchical Mode Association Clustering with an R Package Modalclust
Yansong Cheng1, Surajit Ray2
1Quantitative Science, Glaxo Smith Kline, King of Prussia, King of Prussia, Pennsylvania, USA
2School of Mathematics and Statistics, Glasgow University, Glasgow, UK
Email: yansong.x.cheng@gsk.com, surajit.ray@glasgow.ac.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 September 2014; revised 20 October 2014; accepted 5 November 2014
ABSTRACT
Modalclust is an R package which performs Hierarchical Mode Association Clustering (HMAC) along with its parallel implementation over several processors. Modal clustering techniques are especially designed to efficiently extract clusters in high dimensions with arbitrary density shapes. Further, clustering is performed over several resolutions and the results are summarized as a hierarchical tree, thus providing a model based multi resolution cluster analysis. Finally we implement a novel parallel implementation of HMAC which performs the clustering job over several processors thereby dramatically increasing the speed of clustering procedure especially for large data sets. This package also provides a number of functions for visualizing clusters in high dimensions, which can also be used with other clustering softwares.
Keywords:
Modality, Kernel Density Estimate, Mode, Clustering

1. Introduction
Cluster analysis is a ubiquitous technique in statistical analysis that has been widely used in multiple disciplines for many years. Historically cluster analysis techniques have been approached from either a fully parametric view, e.g. mixture model based clustering, or a distribution free approach, e.g. linkage based hierarchical clustering. While the parametric paradigm provides the inferential framework and accounts for the sampling variability, it often lacks the flexibility to accommodate complex clusters and are often not scalable to high dimensional data. On the other hand, the distribution free approaches are usually fast and capable of uncovering complex clusters by making use of different distance measures. However, the inferential framework is distinctly missing in the distribution free clustering techniques. Accordingly most clustering packages in R also fall under the two above mentioned groups of clustering techniques.
This paper describes a software program for cluster analysis that can knead the strengths of these two seemingly different approaches and develop a framework of parallel implementation for clustering techniques. For most model based approaches to clustering, the following limitations are well recognized in the literature: 1) the number of clusters has to be specified; 2) the mixing densities have to be specified, and as estimating the parameters of the mixture models is often computationally very expensive, we are often forced to limit our choices to simple distributions such as Gaussian; 3) computational speed is inadequate especially in high dimensions and this coupled with the complexity of the proposed model often limits the use of model-based techniques either theoretically or computationally; 4) it is not straightforward to extend model-based clustering to uncover heterogeneity at multiple resolutions, similar to the one offered by to the model free linkage based hierarchical clustering.
Influential work towards resolving the first three issues has been carried out in [1] -[7] . Many previous approaches have focused on model selection of mixtures by choosing the number of components, merging existing components or by determining the covariance structure of the mixture density under consideration, see [8] - [10] . They work efficiently if the underlying distribution is chosen correctly, but none of these model based approaches is designed to handle a completely arbitrary underlying distribution (see Figure 5 for one such example). That is, we think that limitations due to issues (3) and (4), above often necessitate the use of model- free techniques.
This paper describes a software program for cluster analysis that can knead the strengths of these two seemingly different approaches and develop a framework of parallel implementation for clustering techniques. The hierarchical mode association clustering―HMAC [11] , which is constructed by first determining modes of the high-dimensional density and then associating sample points to those modes, is the first multivariate model based clustering approach resolving many of the drawbacks of standard model-based clustering. Specifically, it can accommodate flexible subpopulation structures at multiple resolutions while retaining the desired natural inferential framework of parametric mixtures. [12] developed the inference procedure to the number of clusters of this approach. Modalclust is the package implemented in R (R Development Core Team, 2010) for carrying out HMAC along with its parallel implementation (PHMAC) over several processors. Though mode-counting or mode hunting has been extensively used as a clustering technique, most implementation are limited to univariate data. Generalization to higher dimensions was limited both due to the computational complexity of finding modes in higher dimension and the lack of any natural framework to study the inferential properties of modes in higher dimensions. The HMAC provides a computationally fast iterative algorithm for calculating the modes and thereby providing a clustering approach which is scalable to high dimensions. This article provides the description of the R package that implements HMAC and additionally provides an wide array visualization tools for representing clusters in high dimensions. Further, we propose a novel parallel implementation of the approach which dramatically reduces the computational time especially for large data sets, both in data dimen- sions and the number of observations.
This paper is organized as follows: Section 2 briefly introduces the algorithm of Modal Expectation Maximi- zation (MEM) and builds the notion of mode association clustering technique. Section 3 describes a parallel computing framework of HMAC along with computing time comparisons. Section 4 illustrates the implemen- tation of clustering functions in the R package Modalclust along with examples of the plotting functions especially designed for objects of class hmac. Section 5 provides the conclusion and discussion. Comparison of Modal clustering with other popular model based and model free techniques are provided in the supplementary document.
2. Modal EM and HMAC
The main challenge for using mode-based clustering in high dimensions is the cost of computing modes, which are mathematically evaluated as local maximas of the density function with support on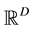 ,
,
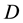 being the data dimension. Traditional techniques of finding local maxima, such as “hill climbing” works well for univariate data. But multivariate hill climbing is computationally expensive thereby limiting its use in high dimensions. [9] proposed an algorithm that solves a local maximum of a kernel density by ascending iterations starting from the data points. Since the algorithm is very similar to Expectation Maximization (EM) algorithm, it is named as
being the data dimension. Traditional techniques of finding local maxima, such as “hill climbing” works well for univariate data. But multivariate hill climbing is computationally expensive thereby limiting its use in high dimensions. [9] proposed an algorithm that solves a local maximum of a kernel density by ascending iterations starting from the data points. Since the algorithm is very similar to Expectation Maximization (EM) algorithm, it is named as
Modal Expectation Maximization (MEM). Define the mixture density as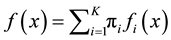 . Now, given any
. Now, given any
initial value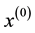 , the MEM solves a local maximum of the mixture density by alternating the following two steps until it meets some user defined stopping criterion.
, the MEM solves a local maximum of the mixture density by alternating the following two steps until it meets some user defined stopping criterion.
1. Let
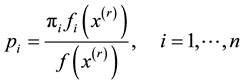
2. Update
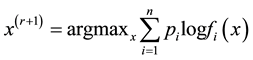
Details of convergence of the MEM approach can be found in [11] . The above iterative steps provide a computationally simpler approach than grid search method for “hillclimbing” from any starting point
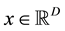 by exploiting the properties of density functions.Given a multivariate kernel
by exploiting the properties of density functions.Given a multivariate kernel , let the density of the data be given by
, let the density of the data be given by
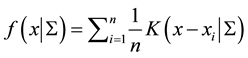
where
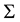 is the matrix of smoothing parameters. Further, in the special case of Gaussian kernels, i.e.,
is the matrix of smoothing parameters. Further, in the special case of Gaussian kernels, i.e.,
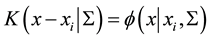
where
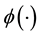 is the pdf of a Gaussian distribution, the update of
is the pdf of a Gaussian distribution, the update of
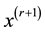 is simply
is simply
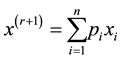
allowing us to avoid the numerical optimization of Step 2.
Now we present the HMAC algorithm. First we scale the data and use a kernel density estimator, with a normal kernel to estimate the density of the data. The variance of the kernel,
 is a diagonal matrix with all entries
is a diagonal matrix with all entries
 denoted by
denoted by


1. Given a set of data


2. Use







3. Extract distinctive values from the set






4. If





We note that when the bandwidth











1. Start with the data




2.
3. Form kernel density as in (1.1) using
4. Cluster the elements in



5. If









6. Stop if
3. Parallel HMAC
In this section we develop the method of parallel computing of HMAC (PHMAC) and its application together with some comparisons of performance of the parallel and non-parallel approach. The MAC approach is computationally expensive when the number of objects






Step 1. Sphering transform the data


Step 2. Let




Step 3. Perform HMAC on each of these subsets at the lowest resolution, i.e., using



Step 4. Pool the modes from each subset of data to form
Step 5. Perform HMAC starting from Step 2 and obtain the final hierarchical clustering.
Step 6. Transform


Figure 1 shows one PHMAC example on the graph. In this figure, (a) shows the simulated data with four clusters along with the contour plot, where the color indicates the final clustering using PHMAC; (b) shows the four random partitions of the unlabeled data along with the modes (red asterisks) at each partition; (c) shows the mode obtained from the four partitions; (d) shows the final modes (green triangles) starting from the modes of the partitioned data. A demonstration of different steps of parallel clustering with four random partitions is given in Figure 1. The original data set is partitioned into 4 random subsets, and initial modal clustering is performed within the partitions. In the next step, the modes of each of these partitions are merged to form the overall modal clusters in Figure 1(c).
Modes have a natural hierarchy and it is computationally easy to merge modes from different partitions. In practice, we need to decide the best choice of the partition and how many partitions to use. In this section, we provide some guidelines regarding the choices, without exploring their quality in details. In the absence of any other knowledge, one should randomly partition the data. Other choices include partitioning data based on certain coordinates which form a natural clustering, and then taking products of a few of those coordinates to build the overall partition. This strategy might increase the computational speed by restricting the modes within a relatively homogeneous set of observations. Another choice might be to sample the data and build partitions based on the modes of the sampled data.
The PHMAC we proposed uses parallel computing at the first level of HMAC and then use non-parallel computing from the second level onwards. Therefore, the number of partitions to minimize the computational time is a complex function of the number of available processors, the number of observations and the bandwidth parameter of the KDE. If one uses too many partitions, one might speed up the first step, but would have the risk of ending up with too many modes for the next level, where the hill climbing is done from the collection of modes from each partition with respect to the overall density. In contrast, for a large
We compare the computing speed of parallel versus serial clustering using 1, 2, 4, 8 and 12 multi-core processors. Tests were performed on a 64 bits 4 Quad Core AMD 8384 (2.7 Ghz each core), with 16 GB RAM
Figure 1. Steps in parallel HMAC procedure for a simulated data set.
running Linux Centos 5 and R version 2.11.0 From Table 1, it is clear to observe that parallel computing significantly increases the computing speed. Because the KDE is a sum of kernels centered at every data point, the amount of computation needed to identify the mode associated with a single point grows linearly with







Table 1. Comparison of computing time (elapsed time in seconds) using different number of processors.
maximum 12 processors. For



The R package Modalclust was created to implement the HMAC and PHMAC. There are also some plotting tools that give the user a comprehensive visual and understanding of the clustering result. Sources, binaries and documentation of Modalclust are available for download from the Comprehensive R Archive Network http://cran.r-project.org/ under the GNU Public License.
4. Example of Using R Package Modalclust
In this section, we demonstrate the usage of the functions and plotting tools that are available in the Modalclust package.
4.1. Modal Clustering
First, we provide an example of performing modal clustering to extract the subpopulations in the logcta20 data. The description of the dataset is given in the package. The scatter plot, along with its smooth density, is provided in Figure 3. First, we use the following command to download and install the package:
R > install.packages (“Modalclust”)
R > library (“Modalclust”)
Using the following command, we can get the standard (serial) HMAC and parallel HMAC using two pro- cessors for logctA20 data.
R > logcta20.hmac < −phmac(logcta20,npart=1,parallel=FALSE)
R > logcta20p2.hmac < −phmac(logcta20,npart=2,parallel=TRUE)
Both implementation results are given in Figure 4, which clearly identifies the three distinct subpopulations. Other model-based clustering methods, such as EM-clustering or K-means, could not capture the subpopulation structure, as the individual subpopulation is not a normal density. Distance based clustering method e.g., hierarchical clustering, with a range of linkage functions performed even worse.
By default, the function selects an interesting range of smoothing parameters with ten

R > logcta20.hmac$sigma
[1] 0.26 0.29 0.31 0.34 0.38 0.43 0.49 0.58 0.72 0.94,
which are chosen using the spectral degrees of freedom criterion introduced in [10] . Though we started with 10 different smoothing levels, the final clustering shows only 6 different levels along with a decreasing number of hierarchical cluster.
Figure 2. Comparison of fold increase in time for clustering two dimensional data of different sample sizes with respect to using 12 processors.
Figure 3. Smoothing scatter plot of logctA20 data.
Figure 4. HMAC output of logctA20 data.
R > logcta20.hmac$level
[1] 1 2 3 3 3 4 4 4 5 6
R > logcta20.hmac$n.cluster
[1] 11 7 5 5 5 3 3 3 2 1
The user can also provide smoothing levels using the option sigmaselect in phmac. There is also the option of starting the algorithm from user defined modes instead of the original data points. This option becomes handy if the user wishes to merge clusters obtained from other clustering methods, e.g., EM-clustering or K-means.
4.2. Some Examples of Plotting
There are several plotting functions in Modalclust, which can be used to visualize the output from the function phmac. The plotting functions are defined on object class hmac, which is the default class of a phmac output. These plot functions will be illustrated through a data set named disc2d, which has 400 observations displaying the shape of two half discs. The scatter plot of disc2d along with its contour plot are given in Figure 5.
First, we introduce the standard plot function for an object of class “hmac”. This unique and informative plot shows the hierarchical tree obtained from modal clustering. It can be obtained by
R > data (“disc2d.hmac”)
R > plot (disc2d.hmac)
The dendrogram obtained from the disc2d data is given in Figure 6. The

Figure 5. The scatter plot of disc2d data along with its probability contours.
Figure 6. Hierarchical tree (Dendrogram) of disc2d data showing the clustering at four levels of smoothing.
including starting the tree from a specific level, drawing the tree only up to a desired number of clusters, and comparing the clustering results with user defined clusters.
There are some other plotting functions that are designed mainly for visualizing clustering results for two dimensional data, although one can provide multivariate extensions of the functions by considering all possible pairwise dimensions. One can obtain the hard clustering of the data for each level using the command
R > hard.hmac(disc2d.hmac)
Alternatively, the user can specify the hierarchical level or the number of desired clusters, and obtain the corresponding cluster membership (hard clustering) of the data. For example, the plot in Figure 7 can be obtained by either of the following two commands:
R > hard.hmac (disc2d.hmac, n.cluster=2)
R > hard.hmac (disc2d.hmac, level=3)
Another function, which allows the user to visualize the soft clustering of the data, is based on the posterior probabilities of each observation belonging to the clusters at a specified level. For example, the plot in Figure 8 can be obtained using
R > soft.hmac (disc2d.hmac, n.cluster=3)
Figure 7. Hard clustering for disc2d data at level 3.
Figure 8. Soft clustering for disc2d data at level 2.
The plot enables us to visualize the probabilistic clustering of the three cluster model. A user can specify a probability threshold for assigning observations which clearly belong to a cluster or lie in the “boundary” of more than one cluster. Points having posterior probability below the user specified boundlevel (default value 0.4) are assigned as boundary points and colored in gray. In Figure 8, we have five boundary points among the 400 original observations. Additionally, at any specified level or cluster size, the plot=FALSE option in hard.hmac returns the cluster membership. Similarly, plot=FALSE option in soft.hmac returns a list that contains the posterior probability of each observation and boundary points.
R > disc2d.2clust < −hard.hmac (disc2d.hmac,n.cluster=2, plot=FALSE)
R > disc2d.2clust.soft < −soft.hmac (disc2d.hmac,n.cluster=2, plot=FALSE)
5. Discussion
Modalclust performs a hierarchical model based clustering allowing for arbitrary density shapes. Parallel computing can dramatically increase the computing speed by splitting the data and running the HMAC simul- taneously on multi-core processors. Plotting functions give the user a comprehensive visualizing and under- standing of the clustering result. One future work from this stage would be to increase computing speed, especially for large data set. From the discussion in Section 3, it is clear to see, parallel computing increases the computing speed a lot. That relies on the computing equipment. If one user has no multicore or a few multicore processors available, it will take a lot of the computing resources when clustering large data sets. One potential way to solve the computing speed problem is using k-means or other faster clustering techniques initially, and using the HMAC from the centers of each cluster of initial clustering results. For example, if we have a data set with 20,000 observations, we can use k-means clustering and choose a certain number of centers, like 200 centers and run k-means clustering first. And then we start from the centers of 200 clusters and clustering by HMAC. Theoretically it is a sub-optimal way compared with running HMAC for all points. In practice, it is very useful to reduce the computing costs and still obtain the right clustering.
In addition, we are currently working on an implementation of modal clustering for online or streaming data, where the goal would be to update an existing cluster with the new data without storing all the original data points and allowing for creation of new clusters and merging of existing clusters.
Sources, binaries and documentation of Modalclust are available for download from the Comprehensive R Archive Network http://cran.r-project.org/ under the GNU Public License.
Cite this paper
YansongCheng,SurajitRay, (2014) Parallel and Hierarchical Mode Association Clustering with an R Package Modalclust. Open Journal of Statistics,04,826-836. doi: 10.4236/ojs.2014.410078
References
- 1. Fraley, C. (1998) Algorithms for Model-Based Gaussian Hierarchical Clustering. SIAM Journal on Scientific Computing, 20, 270-281.
http://dx.doi.org/10.1137/S1064827596311451 - 2. Fraley, C. and Raftery, A. (1998) How Many Clusters? Which clustering method? Answers via Model-Based Cluster Analysis. The Computer Journal, 41, 578-588.
http://dx.doi.org/10.1093/comjnl/41.8.578 - 3. Fraley, C. and Raftery, A. (1999) Mclust: Software for Model-Based Cluster Analysis. Journal of Classification, 16, 297-306.
http://dx.doi.org/10.1007/s003579900058 - 4. Fraley, C. and Raftery, A. (2002) Model-Based Clustering, Discriminant Analysis, and Density Estimation. Journal of the American Statistical Association, 97, 611-631.
http://dx.doi.org/10.1198/016214502760047131 - 5. Fraley, C. and Raftery, A. (2002) Mclust: Software for Model-Based Clustering, Density Estimation and Discriminant Analysis. Tech. Rep., DTIC Document.
- 6. Ray, S. and Lindsay, B. (2005) The Topography of Multivariate Normal Mixtures. The Annals of Statistics, 33, 2042-2065.
http://dx.doi.org/10.1214/009053605000000417 - 7. Ray, S. and Lindsay, B. (2007) Model Selection in High Dimensions: A Quadratic-Risk-Based Approach. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70, 95-118.
- 8. Baudry, J., Raftery, A., Celeux, G., Lo, K. and Gottardo, R. (2010) Combining Mixture Components for Clustering. Journal of Computational and Graphical Statistics, 19, 332-353.
http://dx.doi.org/10.1198/jcgs.2010.08111 - 9. Hennig, C. (2010) Methods for Merging Gaussian Mixture Components. Advances in Data Analysis and Classification, 4, 3-34.
http://dx.doi.org/10.1007/s11634-010-0058-3 - 10. Tantrum, J., Murua, A. and Stuetzle, W. (2003) Assessment and Pruning of Hierarchical Model Based Clustering. Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 197-205.
http://dx.doi.org/10.1145/956750.956775 - 11. Li, J., Ray, S. and Lindsay, B. (2007) A Nonparametric Statistical Approach to Clustering via Mode Identification. Journal of Machine Learning Research, 8, 1687-1723.
- 12. Cheng, Y. and Ray, S. (2014) Multivariate Modality Inference Using Gaussian Kernel. Open Journal of Statistics, 4, 419-434.
http://dx.doi.org/10.4236/ojs.2014.45041 - 13. Lindsay, B., Markatou, M., Ray, S., Yang, K. and Chen, S. (2008) Quadratic Distances on Probabilities: A Unified Foundation. The Annals of Statistics, 36, 983-1006.
http://dx.doi.org/10.1214/009053607000000956










