Received 30 July 2014; revised 2 September 2014; accepted 12 September 2014

ABSTRACT

We show that most of the empirical or semi-empirical isotherms proposed to extend the Langmuir formula to sorption (adsorption, chimisorption and biosorption) on heterogeneous surfaces in the gaseous and liquid phase belong to the family and subfamily of the Burr_XII cumulative distribution functions. As a consequence they obey relatively simple differential equations which describe birth and death phenomena resulting from mesoscopic and microscopic physicochemical proc- esses. Using the probability theory, it is thus possible to give a physical meaning to their empirical coefficients, to calculate well defined quantities and to compare the results obtained from different isotherms. Another interesting consequence of this finding is that it is possible to relate the shape of the isotherm to the distribution of sorption energies which we have calculated for each isotherm. In particular, we show that the energy distribution corresponding to the Brouers- Sotolongo (BS) isotherm [1] is the Gumbel extreme value distribution. We propose a generalized GBS isotherm, calculate its relevant statistical properties and recover all the previous results by giving well defined values to its coefficients. Finally we show that the Langmuir, the Hill-Sips, the BS and GBS isotherms satisfy the maximum Bolzmann-Shannon entropy principle and therefore should be favoured.

Keywords:

Adsorption Isotherms, Burr Functions, Adsorption Energy Distribution, Maximum Entropy

1. Introduction

Every year hundreds or more papers are devoted to the analysis of sorption (physical adsorption, chemi- and bio-sorption) of gas or solutions on a variety of substrates [2] . Among them, a great number are concerned with the decontamination of air, water and soil. One of the typical procedures is a comparison of the data with empirical isotherm formulas which in the course of time have been proposed by scientists working in the field to generalize the original Langmuir isotherm to heterogeneous surfaces and to sorption in solutions. Most of these formulas are empirical and bring little information on the physicochemical processes responsible for the particular shape of the isotherm curves. The evolution of the empirical parameters with external factors is recorded but there are no precise correlations between the variations of the parameters belonging to different isotherms. It appears that some order should be introduced in that field in order to propose a more rigorous classification of the sorbent-sorbate couples.

In this paper which is a contribution to that effort, we want to emphasize that since some of these isotherms appear to be genuine cumulative probability distributions, they should be favoured, formulated in the language of the theory of probability and might bring more quantitative and more structured information making advantage of their mathematical properties. The probability theory of complex systems has made considerable progress these last years and one can expect that its introduction in the field of sorption could be of great help.

2. Sorption on Heterogeneous Surfaces

A few years ago we published a paper [1] actualizing the efforts initiated by Langmuir, Zeldowitsch and followers eighty years ago to incorporate in the classical Langmuir adsorption isotherm theory, the heterogeneous nature of the substrate, the N-body interactions and the nonequilibrium state of the sorbate. One important conclusion of this study was that the most important ingredient playing a role in designing the shape of the isotherm is the sorption energy distribution which itself is a reflection of the disordered and complex nature of the phenomenon. In our work, we insisted on the fact that it would be useful to rewrite the theory in the framework of the theory of probability. Moreover we reminded that it is an asymmetric birth and death (sorption-desorption) process and a rare event dominated problem due to the very nature of the sorption mechanism, the more active sites being the first to be occupied. We pointed out that these characteristics should be taken into account in the theory. We showed that to account for the power law Freundlich isotherm, one has to assume a Lévy heavy tail behavior for the temperature dependent Langmuir parameter.

As a consequence of this study we proposed an isotherm using a Weibull distribution known since as Brouers-Sotolongo (BS) isotherm which has been used among others in sorption on porous/nonporous surface interface [3] , magnetic nano-particles [4] , adsorption on doped nanostructures [5] , on activated carbon produced from natural products [6] - [8] , algae [9] - [11] , soils and natural wastes [12] for water treatment [9] [13] , biosorp- tion and biodegradation, food contamination [14] as well as medical applications such as the chemical immobili- zation of bacteriophages on surfaces [15] [16] .

The present paper is a extension of some of the ideas developed in our previous works. We will take advantage of the recent progress in the statistical theory of complex and deterministic chaotic systems. We will show that many of the isotherms used in the literature, especially in the treatment of water, form a subfamily of the Burr_XII distribution. This will lead us to propose a generalization (GBS) of the BS isotherm replacing the exponential in the Weibull function by a deformed exponential used now in the formulation of the nonextensive thermodynamics [17] and other complex systems theories. The same technique has helped us to elucidate the universality of relaxation in disordered systems [18] [19] and formulate a fractional-time kinetics for n-order reaction systems [20] . As we will show, many of the isotherms used in the literature can be obtained by giving well defined values to the parameters of this generalized isotherm.

3. The Burr_XII Distribution Function

If we view the isotherm as a cumulative distribution function we can write the isotherms in the following forms:

(1)

In Equation (1), 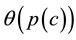is the relative sorbed quantity as the pressure or concentration are increased in the gas or liquid phase in appropriate units. The quantity 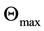is the maximum sorption capacity in appropriate units. The 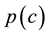are supposed to be related thermodynamically to a sorption energy variable e:

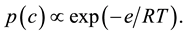(2)

In an heterogeneous system, as we increase the pressure or the concentration, the most active sites with the highest sorption energy are first occupied until complete saturation. With a change of variable, one can write

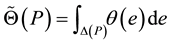(3)

where 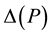is the range of energies involved at pressure 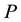and 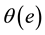is an energy dependent properly normalized distribution function. This second formulation (Equation (3)) has been used to determine an empiri- cal formula for the sorption energy distribution [21] -[24] . In the following the variables 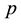or will be de- noted by the greek letter

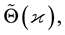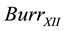We will now demonstrate that if we choose for the cumulative distribution function (cdf) many of the physically sound isotherms used in the literature to generalize the Freundlich formula can be recovered and a new generalized isotherm can be proposed as a synthesis of the efforts of a few generations.

In probability theory and statistical sciences, the 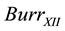distribution is a continuous probability distribution for a non-negative random variable [25] . It is also known in econometrics as the Singh-Maddala distribution [26] where it has been used as a generalization of the Pareto distribution for the graduation over the whole range of incomes and is used to measure the level of inequality.

The 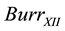distribution is a a member of a system of continuous cumulative distribution (cdf) functions introduced by I. Burr in 1942 [25] . It has the form:

(4)

where are positive parameters. Its normalized probability density function (pdf) is ob- tained from

(5)

(6)

In previous papers [18] [19] , we have shown how it could be derived from the maximum entropy principle using a generalization of the non-extensive Tsallis entropy with appropriate constraints. However more recently, it has been shown that it can be derived more naturally from the classical Boltzmann-Gibbs entropy with appro- priate generalization of the moments constraints (see Section 9).

The cumulative distribution functions belonging to the Burr family are solution of the general differential equation

(7)

where and are continuous functions defined in specific domains. This differential equation describes a birth and death function modulated by a function which applied to a particular problem depends on the nature of the phenomena and the influence of the environment. The first and most studied of these differential equations is the famous Verhulst logistic equation introduced in 1845 [27] to mimic and cal- culate population dynamics. In that case, and its solution is

(8)

In its discrete form it has been one of the first model of deterministic chaos [28] .

For the cdf, the twelfth one in the family, the function has the form of an hyper- bolic type function, the function, varying smoothly between and.

(9)

The distribution function has become a reference distribution in complex and non equilibrium systems as the exponential and Gaussian distributions are the reference distributions in equilibrium and non interacting systems. The “dialectic” form of its differential equation shows that it could be useful to deal with phenomena like for instance epidemic propagation, population evolution, kinetics of complex reactions, eco- nomic evolution, pharmacokinetic, cancer remission and obviously sorption-desorption. It has been used exten- sively these last years in a variety of chaos, nonlinear and nonequilibrium problems in quasi all fields of pure and applied sciences including natural phenomena, meteorology, hydrology, earthquake, economy, sociology and medicine.

An other interesting feature of the distribution is the existence of two power laws tails, one for with exponent and one for with exponent. It has a limited number of finite moments depending on the value of When it has a heavy tail and belongs to the basin of attraction of the family of stable Lévy distributions. It is to say, it has some peculiar properties which have interesting consequences. Lévy functions do not obey the traditional central limit theorem and an expectation value of cannot be defined. For higher values of the average value increases with the number of observations following a well defined power law [29] .

4. The Subfamily of the Burr_XII Distribution and the Associated Isotherms

The function (Equation (4)) can generate a sub-family of cdf distributions if one gives particular values to the two parameters and in. The case and is simply the exponential func- tion. Some of these functions coincide with the form of well known empirical isotherms:

・ For

(10)

(11)

This is a Weibull distribution. The corresponding isotherm in the sorption literature is known as the Brouers- Sotolongo (BS) isotherm:

(12)

If, one gets the Freundlich isotherm

(13)

If moreover one puts in Equation (12), one gets the Jovanovic isotherm [30]

(14)

・ For, one has:

(15)

(16)

which is called in probability theory the loglogistic function. The corresponding isotherms are the Hill, the Langmuir-Freundlich and Sips isotherms

(17)

・ If both and are equal to 1:

(18)

the corresponding isotherm is the Langmuir isotherm.

(19)

As discussed in [1] , the exponent is related to the width and shape of the sorption energy distribution which itself depends on the heterogeneity of the substrate. In Section 8 we will show that it defines an effective temperature

In the isotherms we have just reviewed, the exponent is supposed to be constant and do not change with the evolution of the sorbed quantity This is a restrictive assumption. An isotherm derived from the full would allow the characteristic exponent to vary slowly from to. Therefore quite naturally a more realistic isotherm based on the full distribution can be proposed:

(20)

This generalized BS isotherm has a unified character since it contains the Langmuir, the Freundlich-Langmuir, the Hill and the Sips isotherm and as we will see in the next section, the Generalized Freundlich-Langmuir and the Toth isotherms. The GBS isotherm can be written in a more compact form

(21)

We have used the definition of the deformed exponential function introduced in mathematics in the XIX century and appearing to day in the theory of many complex systems

(22)

(23)

When, one recovers the usual exponential. In the nonequilibriun thermodynamic literature where is the nonextensive (nonadditive) entropy index [17] . In the complex reaction literature, , where is the effective fractional reaction order. In the extreme value theory, the shape parameter of the distribution. We recover the isotherm if and the Hiil-Sips adsorption for.

This new isotherm has four parameters and which have simple physical interpretation: is the maximum saturation sorbed quantity, is the Freundlich exponent which is related to the width and shape of the sorption energy and is a measure of the distribution. When, it can be related to the self- similar (fractal) properties at the micro- and meso-scopic scale. For, it has been interpreted as the mani- festation of a multi-molecular site sorption [31] . The coefficient is related to the cluster organization of the system. A large corresponds to a strong clustering organization [32] . The coefficient b is a T depen- dent scale parameter and combined with and allows the calculation of all the quantities characterizing the statistical distribution: expectation, variance and moments, median, quantiles and some other coefficients which measure quantitatively the way the sorption depends on the concentration or the pressure. These useful expressions for the analysis of isotherms are derived in the appendix. The value separates the distribu- tions defining the isotherms in two groups. For and this includes the Langmuir isotherm, the pdf is L-shaped while for, it is unimodular. This has a strong influence on the nature of the sorption. We will show also in the appendix that the quantity is directly related to specific moment of the probability distri- bution. Finally when is it is the heavy tail (Lévy) exponent which controls the saturation be- havior of the sorption curve.

5. The Generalized Freundlich-Langmuir and Toth Isotherms

A two exponents isotherm (GFL) generalizing the Freundlich-Langmuir (Hill, Sips) isotherm was proposed by Marczewski and Jaroniec [33] .

(24)

The corresponding cdf function

(25)

has the characteristics of a cdf .

It appears that has the form of a Dagun function [34] used concurrently with the equation in econometrics. It can be related to the function by a simple change of variables. This will allow us to relate the isotherms obtained from the GFL isotherm form (20) to the ones already derived.

As, is also the solution of a first order differential equation. Indeed one has

(26)

We have moreover:

(27)

These asymptotic behaviors which are supposed to be the same as the ones of gives the relations between the exponents of the two formulations.

(28)

Starting from the GLF isotherm equation, one can recover some of the empirical isotherms: for the Langmuir isotherm, for, the Langmuir-Freundlich or Hill isotherm. For, the Sips isotherm and for the Toth [35] isotherm. The first ones belong to the subfamily of the subfamily isotherms and have been already considered. The Toth isotherm is applicable only for and for. We will see now how the Marczewski and Jaroniec GLF is linked to the function using the relations between the two probability functions.

6. Dagum Distribution versus Burr_XII Distribution

The Burr_XII cdf and pdf functions (Equations (4), (5)) can be written

(29)

(30)

If we make the change of variables and in (Equations (29) and (30)), we get the Dagum cdf and pdf:

(31)

(32)

Therefore one has the relation

(33)

The relation between the Generalized Freundlich-Langmuir function and the Burr_XII function can be written using the previous results:

(34)

This allows the GLF isotherm and the Toth [35] isotherm as well as the equivalent Oswin isotherm [36] used in food industry to be part of the isotherm family.

The others empirical isotherms [37] [38] correspond to couples of values and in the general form (Equation (25)) which give non physical asymptotic behavior and therefore cannot be used over the whole range of concentration or pressure They might give excellent fit over a limited range of data, like the popular Redlich- Peterson isotherm [37] , but cannot give reliable information over the whole sorption process. The same is true for the Freundlich isotherm. In our opinion, as a logical consequence of our work these isotherms should be discarded since we dispose now, with the unified GBS form (Equations (20), (21)), of a four parameter isotherm with a solid theoretical and physical foundation.

We can now derive quite simply the shape of the sorption energy distribution giving rise to the various isotherms we have just derived.

7. Sorption Energy Distributions

As we already discussed in a previous publication, starting from the thermodynamic relation

(35)

and using the probability theory relation

(36)

it is possible to calculate the sorption energy distribution corresponding to each isotherm. As discussed later, this sorption energy is the energy which governs the macroscopic thermodynamic properties of the system. It is not the microscopic site energies resulting from the atomic and molecular interactions.

In that way we have obtained the following results:

・ For the proposed GBS. isotherm derived from the Burr_XII distribution function:

(37)

The other distributions can be obtained easily:

・ For we have the distribution corresponding to the isotherm

(38)

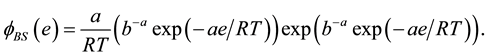
・ For we have the distribution corresponding to the Hill-Sips isotherm:

(39)

It is worth noticing that the BS. distribution has the form of the Gumbel [39] [40] (maximum) extreme value probability distribution function

(40)

(41)

(42)

The standard deviation of this function is well known

(43)

confirming the conclusions of reference [1] about the physical signification of the exponent.

The function corresponding to the new proposed GBS isotherm is one member of the family of generalized Gumbel functions.

(44)

(45)

(46)

It is the symmetric of the Fisher-Tippett [40] [41] generalized extreme value cumulative distribution

(47)

It is worth noticing that this last function (Equation (45)) could have been obtained by using the BS isotherm (Equation (12)) and a c-deformed thermodynamic exponential (see Equation (22)) expression

(48)

To be complete we have calculated the energy distributions corresponding to the Freundlich-Langmuir isotherm

(49)

If (Hill, Sips)

(50)

If (Toth, Oswin)

(51)

If (Generalized-Freundlich)

(52)

Some of the these distributions have been obtained earlier by various authors without reference to the pro- bability theory and using the Cerofolini condensation approximation method [21] . Equation (41) was derived in [22] , Equations (39), (50) was derived in [23] and Equation (52) in [24] . They have been used to determine numerically sorption energy distributions from isotherm data and investigate the thermodynamic nature of the sorption from the measured isotherms. The detailed calculations require assumptions on the range of sorption energy, the integrals being performed from to with respect to a reference energy. As and tend to, one recovers the Langmuir isotherm, the model with a unique sorption energy. Indeed the energy probability density (Equation (39) with) is the derivative of a Fermi function and tends to a Heaviside function as tends to 0. The corresponding pressure or concentration density function has a horizontal asym- ptote at the origin. Physically this means that on a homogeneous surface the pressure range over which sorption takes place (from a few percents to complete coverage) at finite temperature, will be only of one or two order of magnitude, and be narrower as T decreases (and decreases), an observation already discussed by Roginskii [42] .

8. Langmuir, Hill-Sips and Brouers-Sotolongo Isotherms Obey the Maximum Entropy Principle

Before concluding this study it is worthwhile to point out that the distribution functions giving the Langmuir, the Hill-Sips-“Langmuir-Freundlich”, the Brouers-Sotolongo and Generalized Brouers-Sotolongo can be derived maximizing the Boltzmann-Shannon entropy measure:

(53)

using the Lagrange multipliers methods [43] [44] with constraints generalizing the ones used for the Weibull distribution [45] by introducing a c-deformation of the power function

(54)

in the same spirit as the deformation of the exponential function (Equation (22)). One uses the following con- straints:

(55)

(56)

where is the Euler constant and is the BiGamma function.

For (Brouers-Sotolongo) and (Hill-Sips) and Langmuir these constraints can be simplified to

(57)

(58)

which are the well known Weibull constraints and

(59)

(60)

which are the loglogistic constraints. The fact that these isotherms correspond to the maximum entropy show that they are the best and less biased isotherms when the parameters a, b and can be determined experi- mentally and therefore should be favoured amongst all the proposed empirical formulas.

9. Conclusions

In this paper we have shown that a generalized isotherm having the analytical form of a cdf is able to generate a whole family of empirical isotherms used in the literature to represent the sorption data of a great number of solid-gas and solid-liquid sorbate-sorbent couples. Due to the fact that the and associated functions are used extensively in econometrics, there exists on the market efficient nonlinear fitting computing programs and the use of the GBS isotherm should make obsolete the comparison, often with questionable linear fitting, of experimental isotherms with the various approximations of this more general unified isotherm. Practically since the isotherm interpolates nicely between the BS and the Hill-Sips isotherm and since the two parameters isotherms give generally a reasonably good fit, one can first try both of them and then using these partial results improve the fit with the three parameters GBS when this is possible given the generally scarcity of data.

The statistical expressions given in the appendix allow a mathematically well defined characterization of the data. Extensions of the have been proposed with extra parameters. They belong to the Generalized Beta 2 distribution family and are legitimate cumulative probability functions [46] . Such an extension which might be of interest for huge number of data are irrelevant in sorption problems due to the relatively small number of experimental data.

Another important conclusion of this study is that the energy distributions giving rise to the and isotherms belong to the family of extreme value distributions. This is in agreement with the stochastic theory of K. Weron et al. [18] [32] [47] which was developed for relaxation in disordered medias. What matters in highly heterogeneous media is not the detailed microscopic interactions but the extreme value distribution of inter- action energies of dynamically highly correlated mesoscopic clusters (on surfaces, patches, islands). The relation between the phenomenological laws and their microscopic causes has to go through the spatio-temporal scaling properties of these intermediate cooperative regions. This representation allows to average together a large num- ber of extreme probabilistic events to form a predictable picture of the behavior of the entire system. As a con- sequence, the observed tail exponents and and the analytic form of the equations describing the macro- scopic properties are related to the extreme value cluster energy distributions. The parameter defined an effective temperature and is related to the Reyni-Tsallis entropy factor. In catalysis, the appearance of an effective temperature has been traced to the conditions at which the substrate was prepared and annealed. The active centers regarded as defects once in thermal equilibrium at temperature are “frozen” by sudden cooling (quenching) [42] . More generally an effective temperature expresses the fact that, due to the frustrations induced by the geometry and the interactions, the couple sorbate-sorbent is not in thermal equilibrium at the experimental temperature.

Two last remarks have to be made on the range of applicability of the results of this paper. One has to emphasize that it deals with one aspect of sorption i.e. the generalization of the Langmuir isotherm to highly heterogeneous surfaces and solid-liquid interfaces and in some cases of complex composition of sorbates and sorbent. It concerns in particular most works done in water and air decontamination research with pure or treated natural products.

The sorption of simple molecules on smooth surfaces and well defined rough surfaces [48] [49] does not necessarily necessitate an elaborate treatment as used in this paper and the analysis of its isotherms can bring some partial information on the microscopic properties of the surface. In many more complex systems, other phenomena such as wetting, capillarity condensation in pores [50] , as well as diffusion, volume condensation and multi-reactions effects might have to be considered. In those cases, more specific isotherm formulas have to be used [51] . One should also be conscious that the analysis of data with the GBS, Hill-Sips and BS isotherms is relevant only when applied to complete sets of data until saturation.

References

Appendix

The statistical quantities of all isotherms deriving from the unified isotherm will be obtained simply by giving the corresponding values to the coefficient, and to the statistical quantities of that isotherm viewed as a cdf.

What we need to characterize statistically the experimental isotherms are the maximum sorbed quantity corresponding to the saturation the moments of the distribution, the pressure or concentration

corresponding to the maximum sorption rate the quantiles i.e. the value of corresponding to a given percentage of

We can determine the value of when an inflexion point occurs i.e. when the second derivative of the distribution changes sign i.e. at

(61)

For

The expression for the k-th moment is

(62)

where is the Gamma function.

From Equation (62), one can calculate the expectation value and the variance -.

The inverse of the function

(63)

allows us to know the pressure (or the concentration) corresponding to a given percentage of the sorbed quantity.

One can then calculate the quantile solution of, where is the percentage of the

sorbed quantity ranging from 0 to 1. We have therefore using Equation (65):

(64)

(65)

(66)

These are the values of corresponding to a given percentage of the sorbed quantity.

What to do when and an expectation value cannot be calculated? We will show that it is nevertheless possible to calculate finite characteristic quantities which can characterize the distribution.

Starting from the expression of the kth moment (Equation (65)) and choosing the value

(67)

the expression (64) yields

(68)

This statistical quantity can be used to relate the Burr XII to a finite generalized moment which is always finite.

(69)

(70)

The pdf function is the normalized function which maximizes the entropy when the exponents and and the scale factor are known.

Calculating the limits and we can calculate the corresponding expressions for the BS and Hill-Sips isotherms.

In the first case when and using the properties of the function Gamma in Equation (64), one has for any positive value.

(71)

(72)

(73)

For the second case one gets

(74)

(75)

It is convenient to have a relation between and valid for all positive values of. This can be obtained using (64) and the properties of the Gamma function:

(76)

More results can be found in [52] .

All these results can be obtained directly by performing the corresponding integrals.

The characterization of sorption using the values of, , and obtained by the best fit of experimental isotherms using the new methodology derived in this paper is in preparation.