Received 7 January 2014; revised 7 February 2014; accepted 15 February 2014

ABSTRACT

The general functional form of composite likelihoods is derived by minimizing the Kullback-Leib- ler distance under structural constraints associated with low dimensional densities. Connections with the I-projection and the maximum entropy distributions are shown. Asymptotic properties of composite likelihood inference under the proposed information-theoretical framework are established.

Keywords:

Composite Likelihood; I-Divergence; Information Theory; Likelihood Weights; Maximum Entropy Distribution

1. Introduction

The composite likelihood has been increasingly used when the full likelihood is computationally intractable or difficult to specify due to either high dimensionality or complex dependence structures. Consider a random vector X with probability density, where and. Denote the component likelihoods by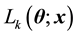, where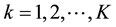, and the composite likelihood proposed in [1] is defined by

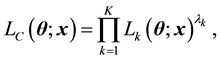
where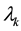’s are non-negative weights to be chosen.

As discussed in [2] , there are two general types of composite likelihood: marginal and conditional composite likelihood. The simplest composite likelihood is the one constructed under the independence assumption:

If the inferential interest is also on parameters prescribing a dependence structure, a pairwise composite likelihood [2] [3] is defined as the following:

Conditional composite likelihood [4] [5] can be constructed by multiplying all pairwise conditional densities:

There are other important variations and applications of the composite likelihoods designed for various inferential purposes such as composite likelihood BIC for model selection in high-dimensional data in [6] . Detailed discussions and review of composite likelihoods were provided in [2] .

Since there are various composite likelihoods with different functional forms, it might be desirable to consider a unifying theme based on information-theoretic justifications. Under an information-theoretic framework, composite likelihoods can then be viewed as a class of inferential functions based on optimal probability density under structural constraints imposed on low dimensional densities when the complete joint density is either unknown or untractable. We show that the optimal densities associated with the composite likelihood are also connected with the I-projection density well-known in probability theory and the maximum entropy distributions in information theory. Although likelihood weights are employed in the original formulation of composite likelihood in [1] , equal weights are often adopted due to convenience. We show that adaptive likelihood weights can indeed improve the performance of composite likelihood inference using equal weights.

This paper is organized as follows. In Section 2, we derive the composite likelihood as the optimal inferential device by minimizing the relative entropy or Kullbak-Leilber distance under structural constraints. Asymptotic properties are established in Section 3. Discussions are given in Section 4.

2. Derivation of Composite Likelihood with Weights

2.1. I-Projection and Maximum Entropy Distribution

Suppose that and 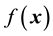are generalized densities of a dominated set of probability measures on the measurable space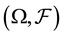. The relative entropy is defined as

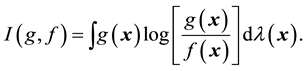
The relative entropy is widely used in information theory and also known as I-divergence in probability. In [7] , Cover and Thomas provide an excellent account on its properties and applications in information theory and coding theory. As demonstrated in [8] , the relative entropy can play an important role in statistical inference. The relative entropy is also called I-divergence and its geometric properties are studied in [9] . Although the relative entropy or I-divergence is not a metric and in general does not define a topology, Csiszár in [9] shows that certain analogies exist between properties of probability distributions and Euclidean geometry, where I-divergence plays the role of squared distance. It is a measure of discrepancy between the probability densities g and f.

For any probability density function (pdf), Csiszár in [9] defines an I-sphere centered around with a radius as the following:

where g is a probability density function.

In statistical inference, the pdf is the model of choice when the true pdf is unknown. In high dimensional or complex cases, it is high unlikely that the assumed model is correct. When no other information on the dependence structure is available, the best model might be the one based on the independent assumption.

When significant characteristics associated with the low dimensional projections of the joint probability density function, it is then desirable to incorporate this information formally into the statistical inference. To improve the chosen model, one might utilize constraints associated with known features under an information theoretic framework to be described in the following. As in [8] , one might consider minimizing with respect to g subject to

(1.1)

where d is a constant vector and a measurable multivariate statistic.

If is a convex set of pdf intersecting, an optimal pdf satisfying

(1.2)

is defined as the I-projection of on in [9] . If such a projection exists, the convexity of guarantees its uniqueness since is strictly convex in g.

The following theorem follows immediately from the above theorem in [9] .

Theorem 1. Given pdf’s, define

where, for,

Then the optimal probability density function (the I-projection of) takes the form

where is the normalizing constant.

Similar to the I-projection, the maximum entropy distribution is also an optimal density under constraints. It is also known as the Maxwell-Boltzmann distribution, the optimal probability density function under temperature constraints. Consider the following maximization problem:

in which satisfying

(1.3)

By applying the maximum entropy theorem in [7] with the constraints set as the logarithm of certain density functions, we then have the following result.

Theorem 2. Let be a set of probability density functions. If we set, , then there exists one unique maximum entropy density function that takes the form:

where is the normalizing constant.

It is clear that the I-projection and the maximum entropy distribution could belong to the same functional class when a set of pdf’s are used to formulate the constraints.

2.2. Derivation of Composite Likelihood Using Pseudo-Metric

If we consider the functional space of all probability density functions satisfying certain conditions and adopt the relative entropy as a pseudo-metric, then a more natural view of point is to seek an optimal density minimizing the relative entropy with constraints characterized by the pseudo distance between the optimal density and a collection of candidate models,.

In the context of composite likelihoods, the statistical model is the joint statistical model assumed while other pdf’s are low dimensional densities to be used to complete the construction of a refined model which may or may not coincides with. For example, one could assume a statistical model under an independence struc-

ture, i.e., where are low dimensional probability density functions. The composite li-

kelihood framework, however, is capable of going beyond this often over-simplified model.

To ensure that the optimal density reflects some known key characteristics in the low dimensional densities of the true pdf, one can apply the idea of I-projection or maximum entropy distribution by considering the following minimization problem:

(1.4)

where are functions of the true joint pdf f. The constraints employed here are different and more natural than those in the I-projection and maximum entropy formulation. In the original setup of the I-projection and maximum entropy distribution, the constraints are expectations of some certain statistics. The theorems of I projection and maximum entropy, however, are no longer applicable as the current set of constraints involves.

We now present our main theorem of this section.

Theorem 3. Given probability density functions, define

where, for,

Then the optimal probability density function satisfying

takes the form

where is a normalizing constant and.

The assertion of this theorem implies that the constraints in the original I-projection can be further generalized such that they are also a functionals of the probability density we seek as well. It can also be seen that , the sphere in the functional space of all probability functions as in the context of I- projection.

The optimal pdf under the current constraints belongs to the following functional class:

(1.5)

where are low dimensional density functions.

We now consider four special cases:

1) (INDEPENDENT CASE) For example, if we assume that, the marginals. Note that we use to denote the marginals in order to distinguish them from the probability density used in the construction. If we set, it then implies that the constraints, which are based on the mar-

ginals only, do not bring in any additional structural information than. Therefore, it follows that the optimal functional density is of the form

if all the weights equal to 1.

2) (CORRELATION CASE) If the constraints are defined by and, it then follows that

The optimal density is then constructed by the marginals and all pairwise bivariate densities. A simplified form is given by

if.

3) (CONDITIONAL CASE) If the constraints are defined by, we can then derive the conditional composite likelihood.

4) (SPATIAL AND TEMPORAL CASE) The weights might be most appropriate for the spatial or temporal settings. Consider for some given t and i. The composite likelihood can also be derived if the Jacobian for transformation is ignored due to its complexity. This would allow spatial and temporal correlation structure to be incorporated.

3. Asymptotic Properties of Composite Likelihood

In this section, we establish the asymptotic properties associated with the composite likelihood inference under the proposed information-theoretic framework. The consistency of the estimators is proved by following the argument in [10] .

For clear presentation, we first define the following notations:

・ Denote the true density function by. Let be the set of density function components under consideration.

・ Denote. The set of probability density functions

with and may not contain the true density function. Put

and.

・ Let be the distance function defined over the space of all density functions. Assume that there is a unique such that. We further assume that

if. For demonstration, is chosen as the K-L divergence in this paper.

・ Let be the estimate of such that

Define

.

We make the following assumptions.

Assumption 1. are measurable, and linearly independent in probability.

Assumption 2. For, for sufficiently small and for sufficiently large.

Assumption 3. If as, then for,

Assumption 4. If, then for,

Assumption 5. if.

Assumption 6. is a closed set.

Assumption 7. is a closed set.

We first give four lemmas in the following before we present the theorems regarding the limiting behavior of the weighted composite likelihood estimators.

Lemma 1. The following hold true:

(L1) Under Assumption 1, is measurable, and hence for any, is measurable.

(L2) Under Assumption 2, is finite for sufficiently small and is finite for sufficiently large.

(L3) Assume that Assumption 3 holds. If as, then

(L4) Assume that Assumptions 4 and 7 holds. If, then

Lemma 2. Assume that Assumptions 1, 2, 6 hold. For any,

Lemma 3. Assume that Assumptions 1 - 3 hold. Then

Lemma 4. Assume that Assumptions 1, 2, 4, 7 hold. Then

The four theorems describing the limiting behavior of the weighted composite likelihood estimators are given below.

Theorem 4. Assume that Assumptions 1 - 6 hold. Let be any closed subset of that does not contain. Then

(1.6)

Theorem 5. Assume that Assumptions 1 - 7 hold. Let be a function of the random samples such that

for any n and for all observations. Then

Theorem 6. Assume that Assumptions 1 - 7 hold. Then, a.s.

Remark 1. Note that in the proof of Theorem 4, the strong law of large numbers is used. If we prove it using the method given in [11] , the consistency of may be extended to a large class of dependent observations.

Remark 2. For simple presentation, we have assumed that are parametric. This restriction is not necessary.

In the following we assume that λ is a constant vector. For easy presentation, define. Let be a solution of the following equations:

For convenience, denote

and

for a twice differentiable function. To investigate the limiting distribution of the composite likelihood estimator, we make the following three more assumptions.

Assumption 8. For each, is twice continuously differentiable in, and satisfies

where and.

Assumption 9. is positive definite, for.

Assumption 10. There exist a positive number and a positive function such that and

for all in the range of.

Define

,

and

We have the following theorem.

Theorem 7. Assume that Assumptions 1 - 10 hold. Then

Remark 3. In light of [12] , the assumptions 1 - 8 made in Theorem 7 may be replaced by the assumptions similar to those assumed in Theorem 4.17 of Shao (2003).

Remark 4. Let be the solution of

By modifying the proof of Theorem 7, can also be shown to be asymptotically normal distributed.

4. Concluding Remarks

The proposed information-theoretic framework provides theoretical justifications for the use of composite likelihood. It also serves as a unifying theme for various seemingly different composite likelihoods and connects them with I-projection and maximum entropy distribution. Significant characteristics of low dimensional models are incorporated into the constraints associated with component likelihoods. Asymptotic properties established in this article could be useful for further theoretical analysis of the properties of the composite likelihoods. The findings presented in this article will lead to more in-depth investigations on the theoretical properties of composite likelihoods and establish some possible connections with information theory.

References

Appendix

Proof of Theorem 1: Let The I-projection is of the form

This completes the proof.

Proof of Theorem 3: By the Lagrange method, we seek to minimize the following objective function

where are Lagrange multipliers.

The objective function can then be rearranged so that

where

Since is not a function of, the first order derivative of g, the Euler-Lagrange equation is then given by

where the derivative is taken with respect to g.

Thus, we have

It then follows that the optimal density function takes the form

where

Proof of Lemma 2: In view of the definition of, the properties of K-L divergence and Lemma 1, Lemma 2 can be proved by following the proof of Lemma 1 of Wald (1949).

Proof of Lemma 3: By Lemma 1, Lemma 3 can be proved by following the proof of Lemma 2 of Wald (1949).

Proof of Lemma 4: By applying Lemma 1, Lemma 4 can be proved by following the proof of Lemma 3 of Wald (1949).

Proof of Theorem 4: By Lemmas 2 and 4, we can find a positive number such that

(1.7)

Let be the subset of consisting of all points of for which. By Lemmas 2 - 3, for each point, there is a such that

(1.8)

Since is a closed set, there exists a finite number of points in such that

where denotes the open sphere with center and radius. Thus,

In light of (1.7)-(1.8), we have

and

Therefore,

which jointly with (1.9) implies (1.6).

Proof of Theorem 5: For any, if a subsequence of that has a limit such that, then for infinitely many,

Hence, for infinitely many n,

By Theorem 4, this event has zero probability. Thus all limit points of satisfy the inequality with probability one, which concludes the theorem.

Proof of Theorem 7: By following the proof of Theorem 4.17 of Shao (2003), it can be shown that

Hence,

which, jointly with Slutsky’s theorem and the central limit theorem, concludes the proof of the theorem.