Open Journal of Statistics
Vol.3 No.3(2013), Article ID:33229,4 pages DOI:10.4236/ojs.2013.33020
Strong Consistency of Kernel Regression Estimate
Department of Statistics and Finance, University of Science and Technology of China, Hefei, China
Email: wqcui@ustc.edu.cn
Copyright © 2013 Wenquan Cui, Meng Wei. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 20, 2013; revised March 23, 2013; accepted April 1, 2013
Keywords: Kernel Regression Estimator; Bandwidth; Strong Pointwise Consistency
ABSTRACT
In this paper, regression function estimation from independent and identically distributed data is considered. We establish strong pointwise consistency of the famous Nadaraya-Watson estimator under weaker conditions which permit to apply kernels with unbounded support and even not integrable ones and provide a general approach for constructing strongly consistent kernel estimates of regression functions.
1. Introduction
Let 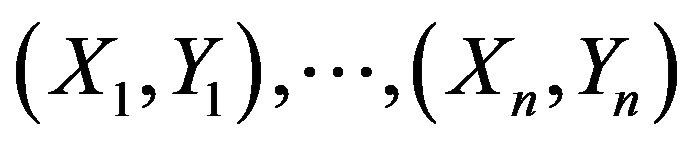 be independent observations of a
be independent observations of a 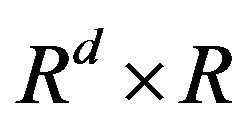 valued random vector (X, Y) with
valued random vector (X, Y) with . We estimate the regression function
. We estimate the regression function 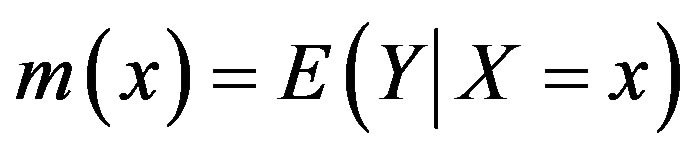 by the following form of kernel estimates
by the following form of kernel estimates
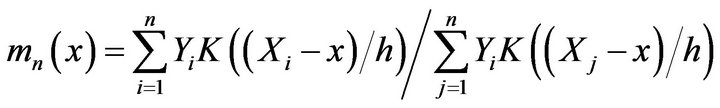 (1.1)
(1.1)
where 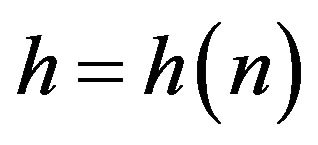 is called the bandwidth and K is a given nonnegative Borel kernel. The estimator (1.1) was first introduced by Nadaraya ([1]) and Watson ([2]). The studies of
is called the bandwidth and K is a given nonnegative Borel kernel. The estimator (1.1) was first introduced by Nadaraya ([1]) and Watson ([2]). The studies of 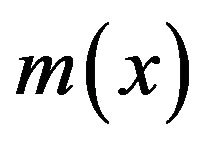 can also refer to, for examples, Stone ([3]), Schuster and Yakowitz ([4]), Gasser and Muller ([5]), Mack and Müller ([6]), Greblicki and Pawlak ([7]), Kohler, Krzyżak and Walk ([8,9]), and Walk ([10]). When point x is near the boundary of their support, the kernel regression estimator (1.1) has suffered from a serious problem of boundary effects. Hereafter 0/0 is treated as 0. For the kernel function we assume that
can also refer to, for examples, Stone ([3]), Schuster and Yakowitz ([4]), Gasser and Muller ([5]), Mack and Müller ([6]), Greblicki and Pawlak ([7]), Kohler, Krzyżak and Walk ([8,9]), and Walk ([10]). When point x is near the boundary of their support, the kernel regression estimator (1.1) has suffered from a serious problem of boundary effects. Hereafter 0/0 is treated as 0. For the kernel function we assume that
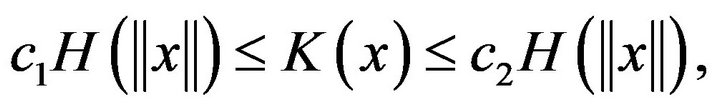 (1.2)
(1.2)
and
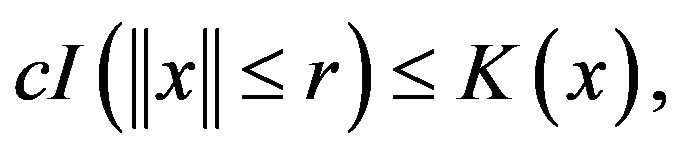 (1.3)
(1.3)
where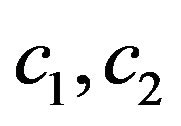 ,
, ![]() and
and 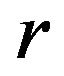 are positive constants,
are positive constants, 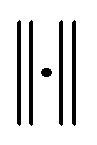 is either always
is either always ![]() or always
or always  norm,
norm, 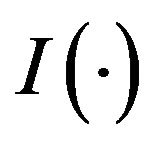 denotes the indicator function of a set, and H is a bounded decreasing Borel function in
denotes the indicator function of a set, and H is a bounded decreasing Borel function in  such that
such that
 (1.4)
(1.4)
Through this paper we assume that
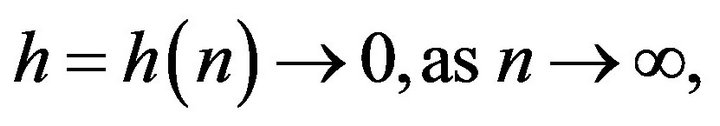 (1.5)
(1.5)
One of the fundamental problems of asymptotic study on nonparametric regression is to find the conditions under which  is a strongly consistent estimate of
is a strongly consistent estimate of 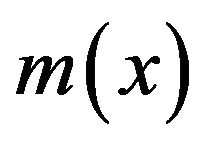 for almost all
for almost all  (µ probability distribution of X). The first general result in this direction belongs to Devroye ([11]), who established strong pointwise consistency of
(µ probability distribution of X). The first general result in this direction belongs to Devroye ([11]), who established strong pointwise consistency of 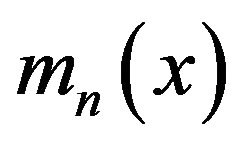 for bounded Y. Zhao and Fang ([12]) establish its strong consistency under the weaker condition that
for bounded Y. Zhao and Fang ([12]) establish its strong consistency under the weaker condition that 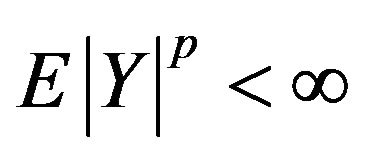 for some
for some . However, the dominating function
. However, the dominating function 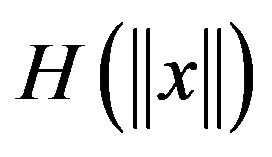 of (1.3) in the above literature is confined as
of (1.3) in the above literature is confined as  for some
for some . GreblickiKrzyżak and Pawlak ([13]) establish the complete convergence of
. GreblickiKrzyżak and Pawlak ([13]) establish the complete convergence of 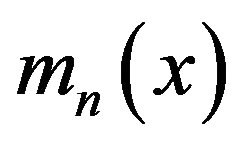 for bounded Y and rather general dominating function H of (1.3) for almost all
for bounded Y and rather general dominating function H of (1.3) for almost all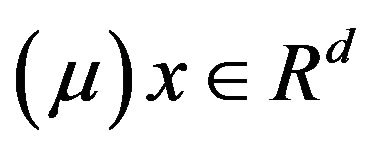 . This permits to apply kernels with unbounded support and even not integrable ones. In this paper, we establish the strong consistency of
. This permits to apply kernels with unbounded support and even not integrable ones. In this paper, we establish the strong consistency of 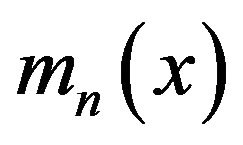 under the conditions of GKP ([13]) on the kernel and various moment conditions on Y, which provides a general approach for constructing strongly consistent kernel estimates of regression functions. We have Theorem 1.1 Assume that
under the conditions of GKP ([13]) on the kernel and various moment conditions on Y, which provides a general approach for constructing strongly consistent kernel estimates of regression functions. We have Theorem 1.1 Assume that 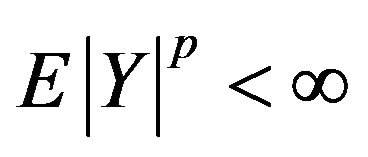 for some
for some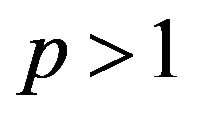 , and (1.2)-(1.5) are satisfied, and that
, and (1.2)-(1.5) are satisfied, and that
 (1.6)
(1.6)
Then
 (1.7)
(1.7)
Theorem 1.2 Assume that  for some
for some 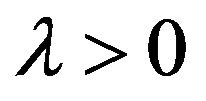 and
and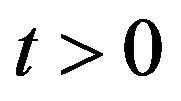 , and (1.2)-(1.5) are met, and that
, and (1.2)-(1.5) are met, and that
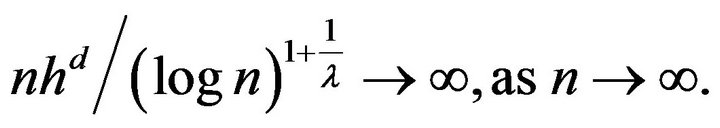 (1.8)
(1.8)
Then (1.7) is true.
It is worthwhile to point out that in the above theorems we do not impose any restriction on the probability distribution µ of X.
2. Proof of the Theorems
For simplicity, denote by c a positive constant, by 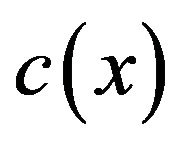 a positive constant depending on x. These constants may assume different values in different places, even within the same expression. We denote by
a positive constant depending on x. These constants may assume different values in different places, even within the same expression. We denote by  as a sphere of the radius r centered at x,
as a sphere of the radius r centered at x,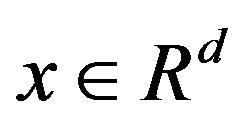 .
.
Lemma 2.1 Assume that . For all
. For all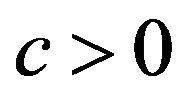 there exists a nonnegative function
there exists a nonnegative function 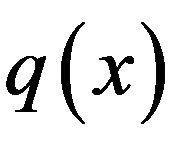 with
with  such that for almost all
such that for almost all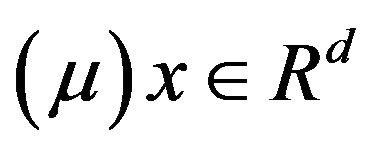 ,
,
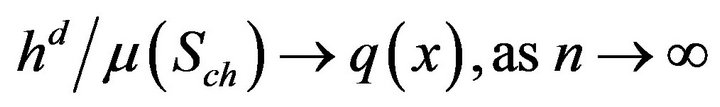
Refer to Devroye ([11]).
Lemma 2.2 Assume that (1.2)-(1.5) are satisfied. Let 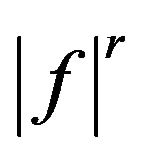 be
be  integrable for some
integrable for some . Then
. Then
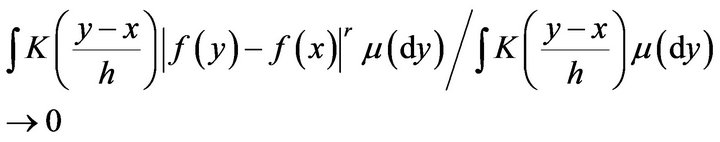
as  for almost all
for almost all .
.
It is easily proved by using Lemma 1 of GKP ([13]).
Lemma 2.3 Assume that (1.2)-(1.5) are met, and that
 .
.
Then for almost all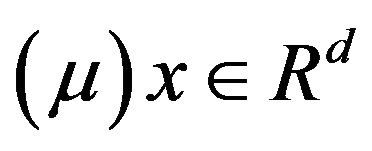

Refer to GKP ([13]).
Now we are in a position to prove Theorems 1.1 and 1.2.
Proof. For simplicity, we write “for a.e. x” instead of the longer phrase “for almost all ”. Write
”. Write
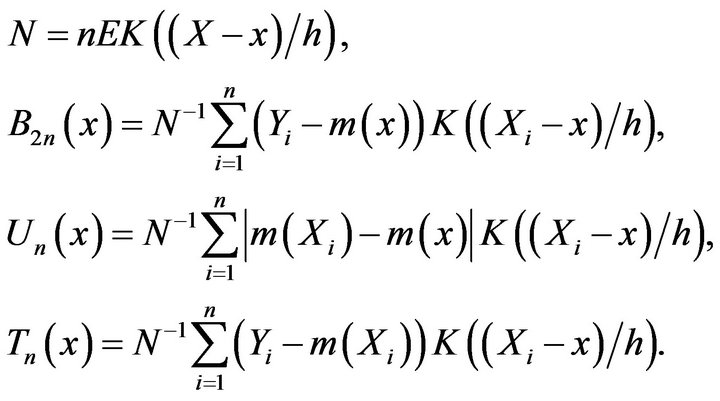
Since
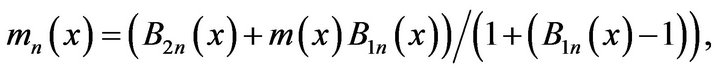
and by Lemma 2.3, a.s. for a.e. x, it suffices to vertify that
a.s. for a.e. x, it suffices to vertify that 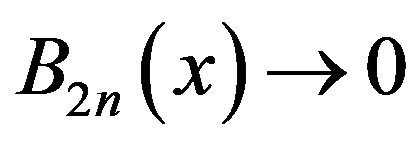 a.s. for a.e. x, or, to prove
a.s. for a.e. x, or, to prove  a.s. and
a.s. and 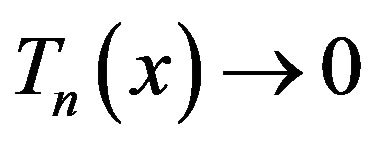 a.s. for a.e. x.
a.s. for a.e. x.
Since 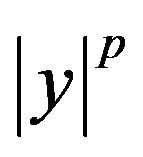 is convex in y for
is convex in y for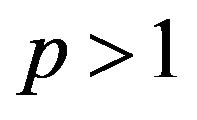 , and for fixed
, and for fixed  and
and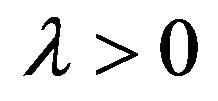 ,
, 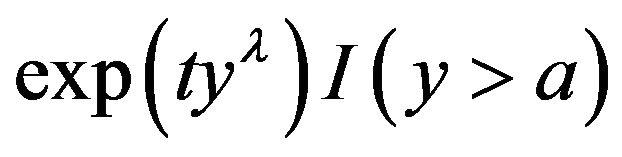 is convex in
is convex in
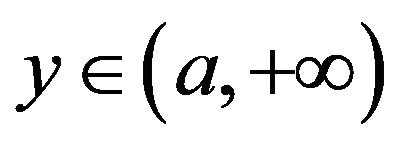 for large a, it follows from Jensen’s inequality that
for large a, it follows from Jensen’s inequality that 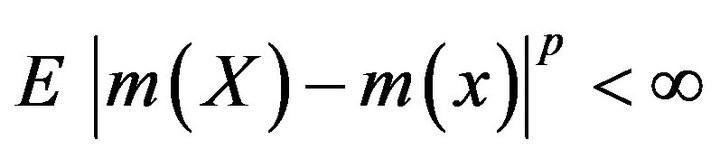 and
and 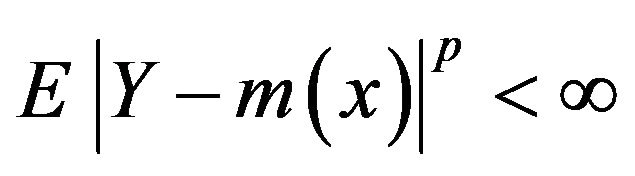
when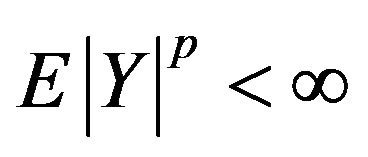 , and that
, and that
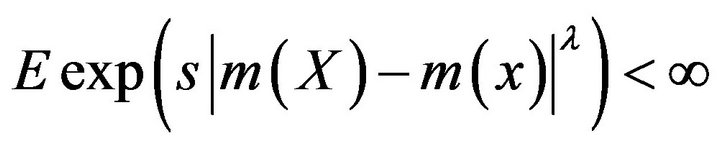 and
and
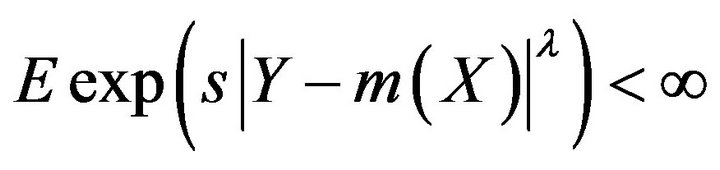 for some
for some 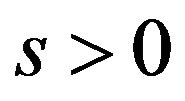 and
and 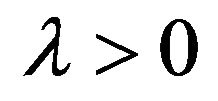
when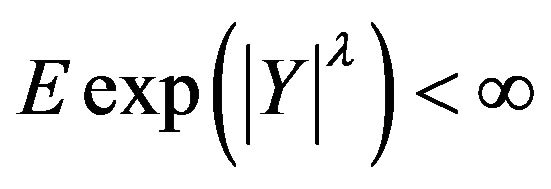 .
.
Write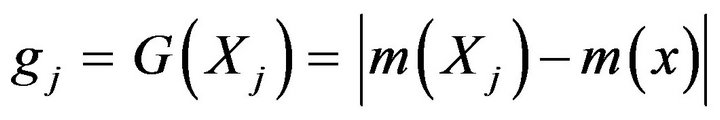 ,
, 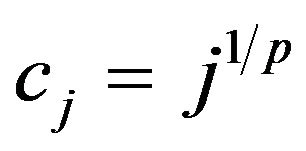 (in Theorem 1.1) or
(in Theorem 1.1) or 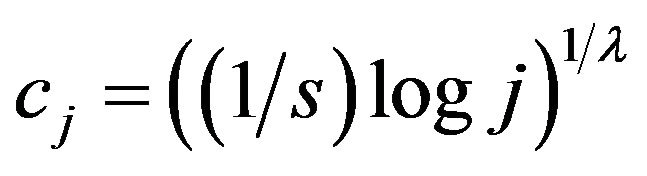 (in Theorem 1.2). It follows that
(in Theorem 1.2). It follows that
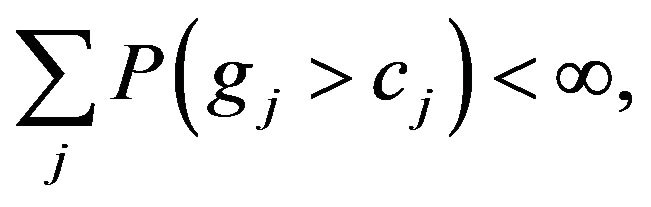
and

by Borel-Cantelli’s lemma, and
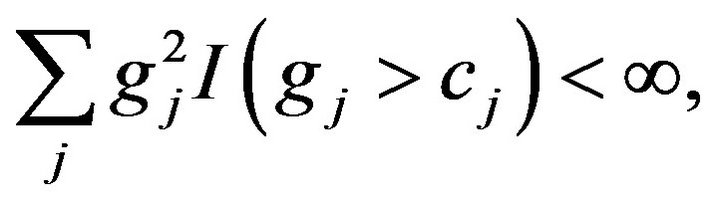 a.s. (2.1)
a.s. (2.1)
Write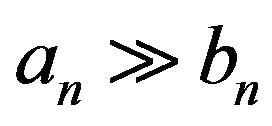 , if
, if . By (1.6) or
. By (1.6) or
(1.8), 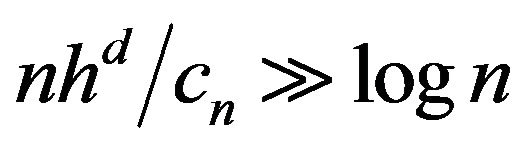 , we can take
, we can take 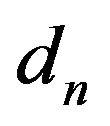 such that
such that
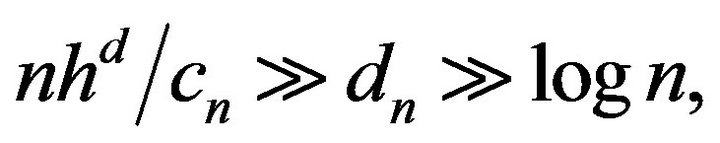 (2.2)
(2.2)
Put
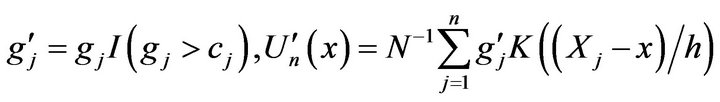
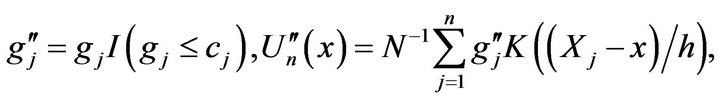
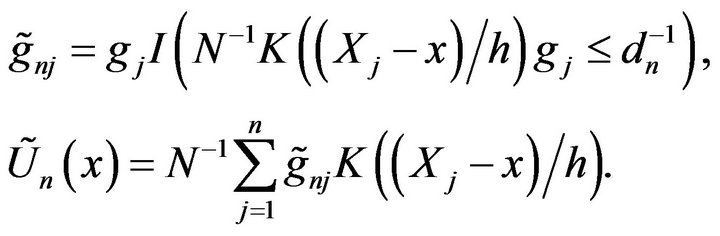
By (1.3) and Lemma 2.1, for a.e. x,
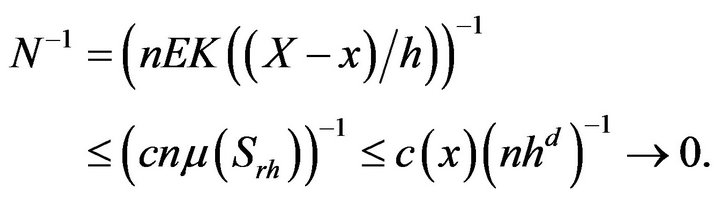 (2.3)
(2.3)
By Lemma 2.3,
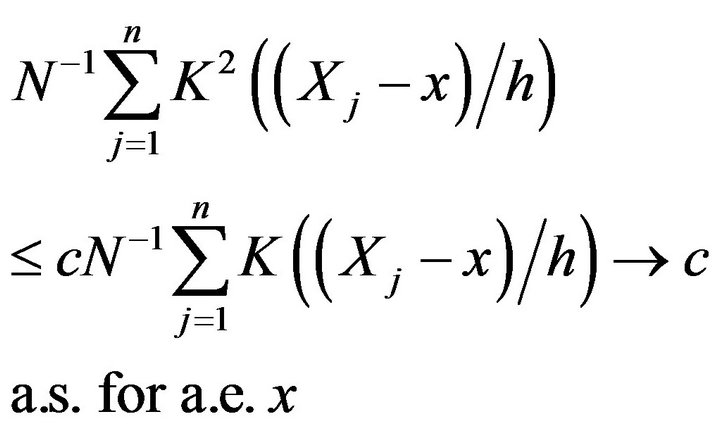 (2.4)
(2.4)
By Schwarz’s inequality, (2.1), (2.3) and (2.4),
 (2.5)
(2.5)
Write
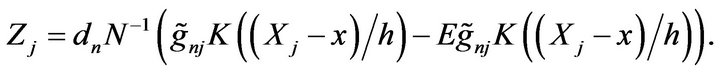
We have  Take
Take
 . Since
. Since 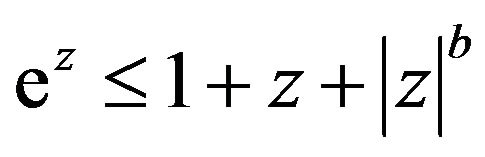 for
for , we have
, we have
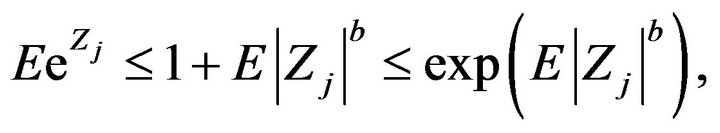
and

By Lemma 2.2,
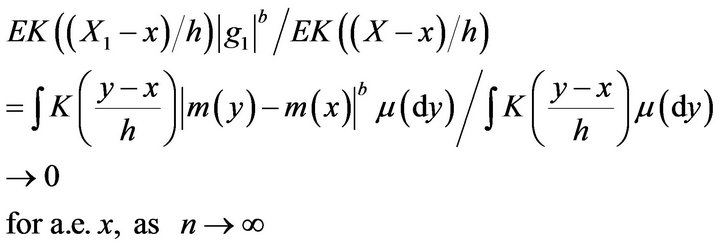 .
.
By (2.2) and (2.3),
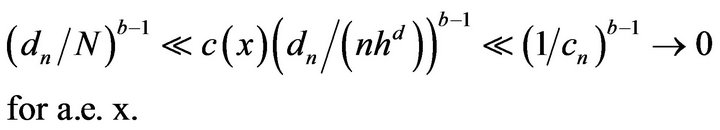
Given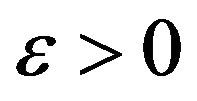 , it follows that for a.e. x and for n large,
, it follows that for a.e. x and for n large,
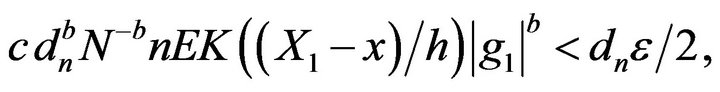 (2.6)
(2.6)
and
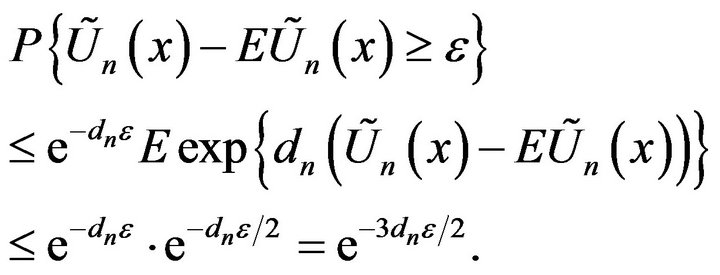
By Borel-Cantelli’s lemma and for a.e. x,
 for any
for any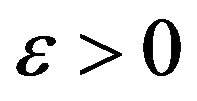 we have
we have
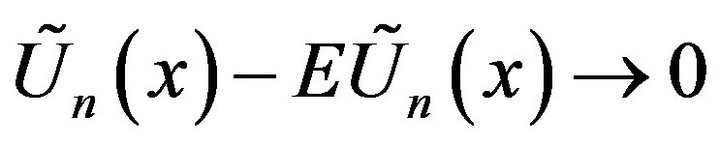 a.s for a.e. x Since, by Lemma 2.2, for a.e. x
a.s for a.e. x Since, by Lemma 2.2, for a.e. x
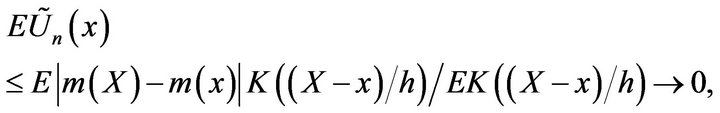
we have
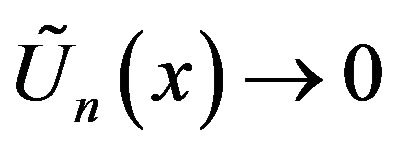 a.s for a.e. x, as
a.s for a.e. x, as![]() . (2.7)
. (2.7)
By (2.2) and (2.3), when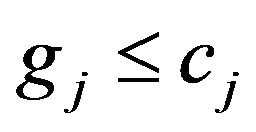 , for a.e. x,
, for a.e. x,
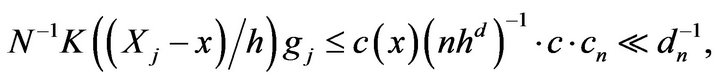
and for n large, 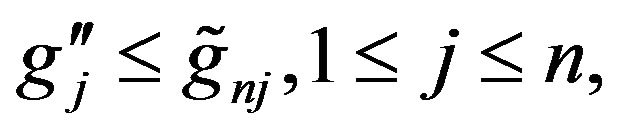 and
and
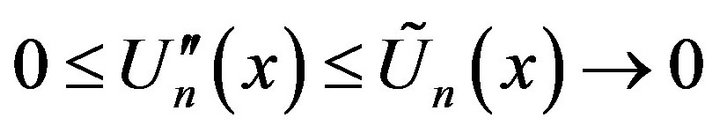 a.s. for a.e. x. (2.8)
a.s. for a.e. x. (2.8)
By (2.5) and (2.8), noticing that 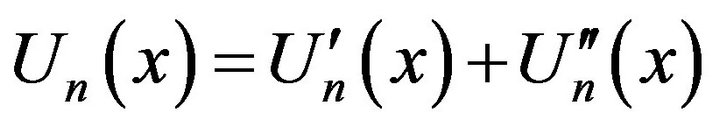 , we have
, we have
 a.s for a.e. x. (2.9)
a.s for a.e. x. (2.9)
To prove 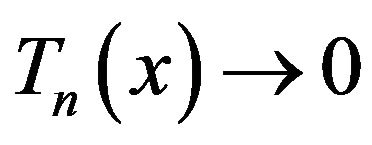 a.s for a.e. x, we write
a.s for a.e. x, we write 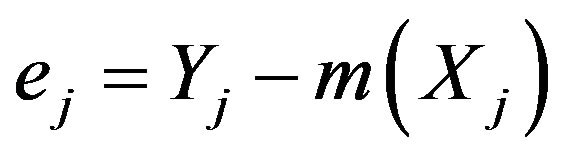 , and put
, and put

By using the same argument as above,
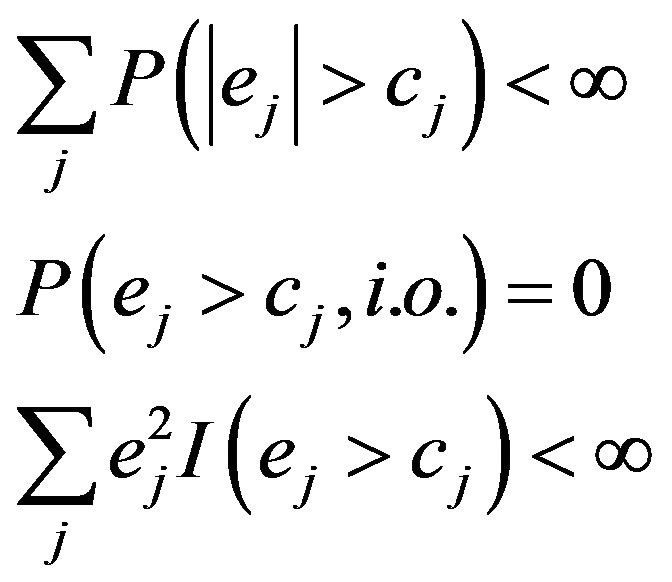 a.s.
a.s.
and for a.e. x,
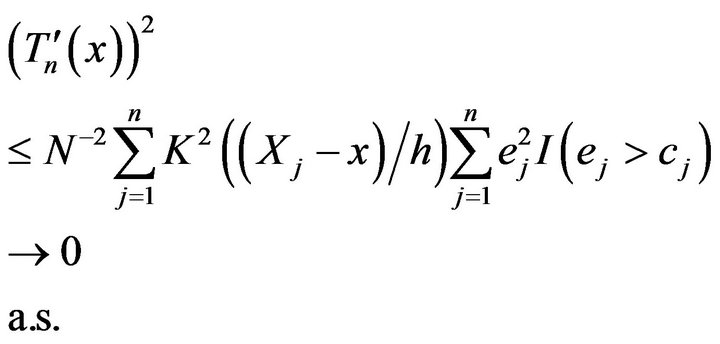 (2.10)
(2.10)
Also, for a.e. x and for n large,
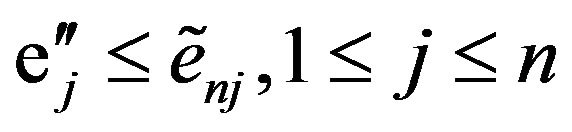 and
and 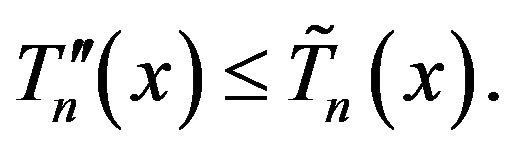 (2.11)
(2.11)
Write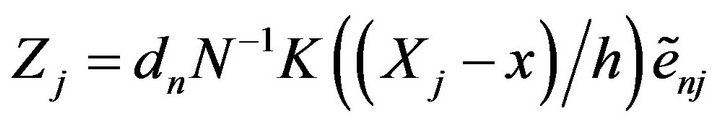 , then
, then
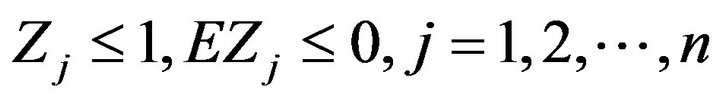 . Take
. Take . Since
. Since
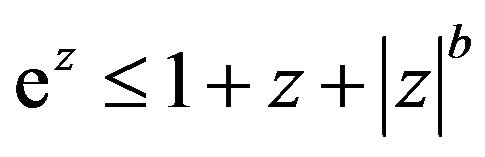 for
for , we have
, we have
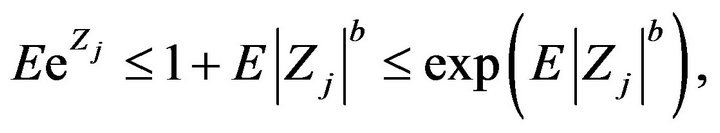
and
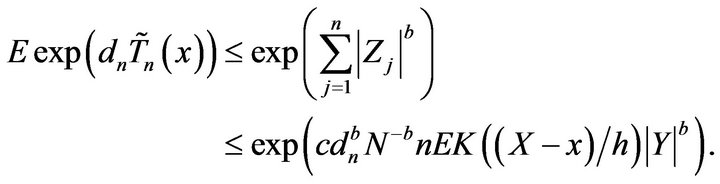
By Lemma 2.2, for a.e. x,

Given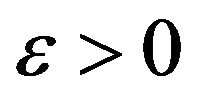 , similar to (2.6), for a.e. x and n large,
, similar to (2.6), for a.e. x and n large,
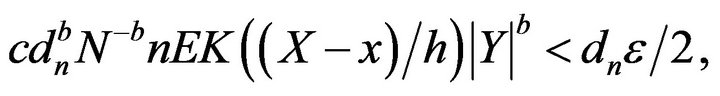 and
and

and it follows that
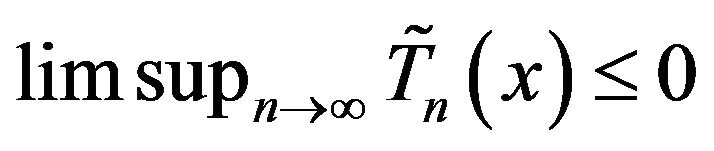 a.s. for a.e. x (2.12)
a.s. for a.e. x (2.12)
from
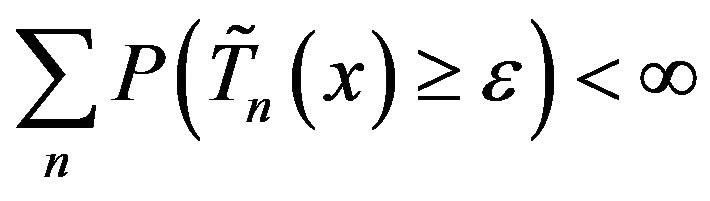 for a.e. x and
for a.e. x and 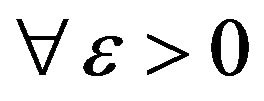
and Borel-Cantelli’s lemma.
By (2.10)-(2.12),
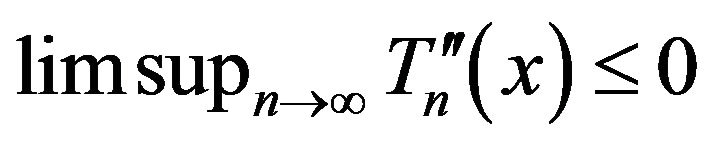 a.s. for a.e. x and
a.s. for a.e. x and
 a.s. for a.e. x (2.13)
a.s. for a.e. x (2.13)
Replacing 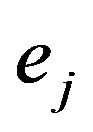 by
by , it implies that
, it implies that
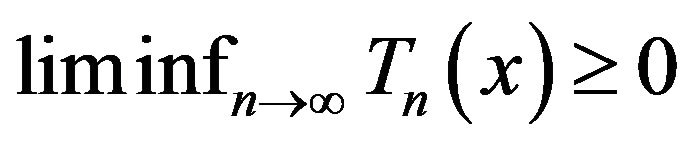 a.s. for a.e. x (2.14)
a.s. for a.e. x (2.14)
(2.13) and (2.14) give
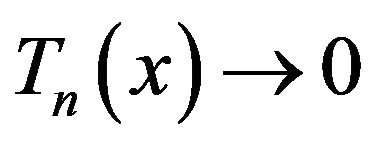 a.s. for a.e. x (2.15)
a.s. for a.e. x (2.15)
The theorems follow from (2.9) and (2.15).
3. Acknowledgements
Cui’s research was supported by the Natural Science Foundation of Anhui Province (Grant No.1308085MA02), the National Natural Science Foundation of China (Grant No. 10971210), and the Knowledge Innovation Program of Chinese Academy of Sciences (KJCX3-SYW-S02).
REFERENCES
- E. A. Nadaraya, “On Estimating Regression,” Theory of Probability and Its Applications, Vol. 9, No. 1, 1964, pp. 141-142. doi:10.1137/1109020
- G. S. Watson, “Smooth Regression Analysis,” Sankhya: The Indian Journal of Statistics, Series A, Vol. 26, No. 4, 1964, pp. 359-372.
- C. J. Stone, “Consistent Nonparametric Regression,” Annals of Statistics, Vol. 5, No. 4, 1977, pp. 595-620. doi:10.1214/aos/1176343886
- E. F. Schuster and S. Yakowitz, “Contributions to the Theory of Nonparametric Regression, with Application to System Identification,” Annals Statistics, Vol. 7, No. 1, 1979, pp. 139-149. doi:10.1214/aos/1176344560
- T. Gasser and H. G. Müller, “Estimating Regression Functions and Their Derivatives by the Kernel Method,” Scandinavian Journal of Statistics, Vol. 11, 1984, pp. 171-185.
- Y. P. Mack and H. G. Müller, “Derivative Estimation in Nonparametric Regression with Random Predictor,” Sankhya: The Indian Journal of Statistics (Series A), Vol. 51, No. 1, 1989, pp. 59-72.
- W. Greblicki and M. Pawlak, “Cascade Non-Linear System Identification by a Non-Parametric Method,” International Journal of Systems Science, Vol. 25, No. 1, 1994, 129-153. doi:10.1080/00207729408928949
- M. Kohler, A. Krzyżak and H. Walk, “Strong Consistency of Automatic Kernel Regression Estimates,” Annals of the Institute of Statistical Mathematics, Vol. 55, No. 2, 2003, pp. 287-308.
- M. Kohler, A. Krzyżak and H. Walk, “Rates of Convergence for Partition-Zing and Nearest Neighbor Regression Estimates with Unbounded Data,” Journal of Multivariate Analysis, Vol. 97, No. 2, 2006, pp. 311-323. doi:10.1016/j.jmva.2005.03.006
- H. Walk, “Strong Universal Consistency of Smooth Kernel Regression Estimates,” Annals of the Institute of Statistical Mathematics, Vol. 57, No. 4, 2005, pp. 665-685. doi:10.1007/BF02915432
- L. Devroye, “On the Almost Everywhere Convergence of Nonparametric Regression Function Estimates,” Annals Statistics, Vol. 9, No. 6, 1981, pp. 1310-1319. doi:10.1214/aos/1176345647
- L. C. Zhao and Z. B. Fang, “Strong Convergence of Kernel Estimates of Nonparametric Regression Functions,” Chinese Annals of Mathematics, Series B, Vol. 6, No. 2, 1985, pp. 147-155.
- W. Greblicki, A. Krzyżak and M. Pawlak, “DistributionFree Pointwise Consistency of Kernel Regression Estimate,” Annals Statistics, Vol. 12, No. 4, 1984, pp. 1570- 1575. doi:10.1214/aos/1176346815

