ABSTRACT

This paper is an extension of Hanif, Hamad and Shahbaz estimator [1] for two-phase sampling. The aim of this paper is to develop a regression type estimator with two auxiliary variables for two-phase sampling when we don’t have any type of information about auxiliary variables at population level. To avoid multi-collinearity, it is assumed that both auxiliary variables have minimum correlation. Mean square error and bias of proposed estimator in two-phase sampling is derived. Mean square error of proposed estimator shows an improvement over other well known estimators under the same case.

1. Introduction

It is fact that precision of estimators of the mean of study variable “y” is increased by proper attachment of highly correlated auxiliary variables. In some situations where auxiliary information is available at population level and cost per unit of collecting study variable “y” is affordable then single-phase sampling is more appropriate. But in a situation where prior information of auxiliary variable is lacking then it is neither practical nor economical to conduct a census for this purpose. The appropriate technique used to get estimates of those auxiliary variables on the basis of samples is two-phase sampling. In such cases we take large preliminary sample and from that auxiliary variables are computed. The main sample is independently sub-sampled from that large sample.

Two-phase sampling is a powerful technique which was firstly introduced by Neyman [2] for the stratification purpose. Two-phase sampling is based on the idea of a sampling design in which nature (specifically the size) of sampling units does not differ at any phase of sampling. “Two-phase sampling is generally employed when number of units, required to give the desired precision on different items, is widely different. This technique is employed to utilize the information collected at the first phase in order to improve the precision of the information to be collected at the second phase” [3].

In two-phase sampling, regression and ratio estimation techniques are used to estimate the finite population mean. Ratio estimator incorporates the prior information closely related to study variable and regression technique is used when relation between study variable and auxiliary variable(s) is linear. Regression estimator is considered to be more useful than ratio estimator except when regression line does not pass through origin otherwise these two estimators have almost same significance and analyst has to decide intuitively.

Let the population consist of units, 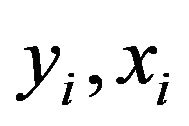and 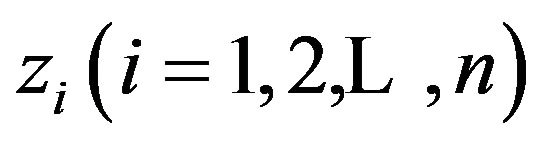denote the values of the i-th unit of the character 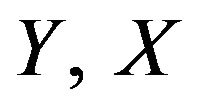and respectively. Here is our variable of interest, is main auxiliary variable and is second auxiliary variable. The two auxiliary variables are highly correlated with variable of interest. Let be first phase sample of size 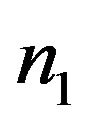from the population of size N according to a simple random sampling without replacement and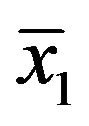, the sample means of two auxiliary variables are observed. Let 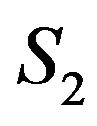be second phase sample of size n₂ from first phase sample and 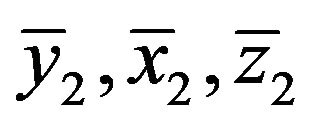are observed. The notations used in this paper are:

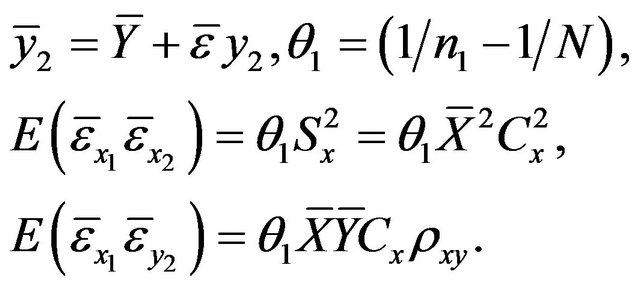(1.1)

Cochran [4] appears to be the first to use auxiliary information in Ratio estimator when there is highly positive correlation between study variable and auxiliary variables. Hansen and Hurwitz [5] were first to suggest the use of auxiliary information in selecting the population with varying probabilities. Robson [6] gave the idea of product estimator when there is highly negative correlation. Two-phase sampling version of [6] is:

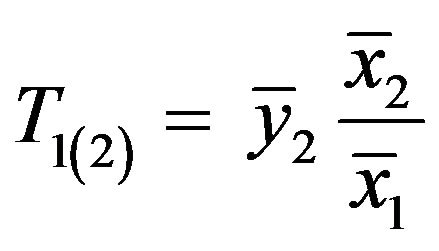, (1.2)

(1.3)

Sukhatme [3] used auxiliary variable in his ratio type estimators for two-phase sampling. One of his estimators was:

, (1.4)

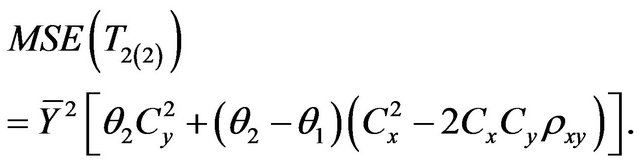(1.5)

Raj [7] proposed a method of using information on several variates to achieve higher precision in two-phase sampling. The two-phase sampling version of [7] is:

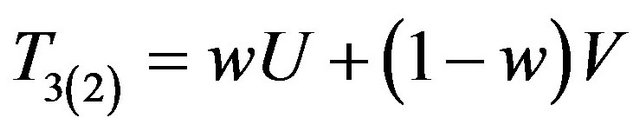(1.6)

where and “w” is a suitably chosen constant.

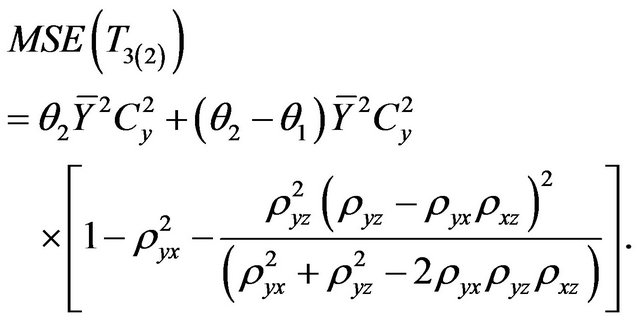(1.7)

Mohanty [8] demonstrated that precision of study variable in two-phase sampling can be increased by combining the regression and ratio estimators using two auxiliary variables.

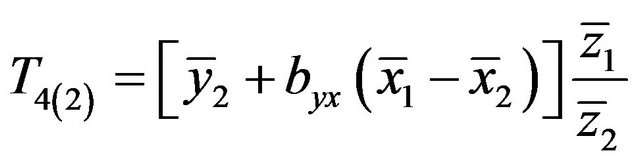, (1.8)

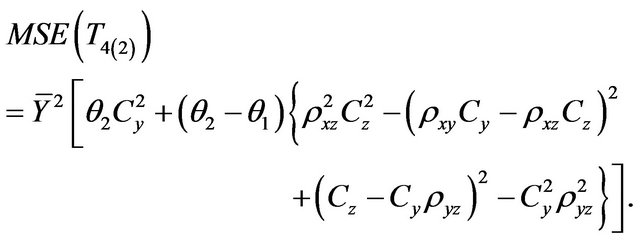(1.9)

Srivastava [9] developed a following class of ratio type estimators:

, (1.10)

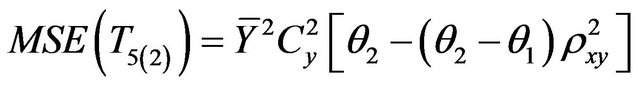. (1.11)

Mukerjee et al. [10] developed three regression type estimators. One was for the situation when no auxiliary information was available.

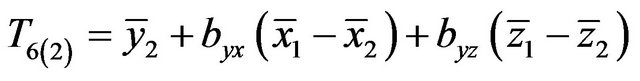, (1.12)

(1.13)

Samiuddin and Hanif [11] developed two-phase sampling version of Sukhatme et al. [12] regression estimator when population means 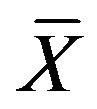and are not known.

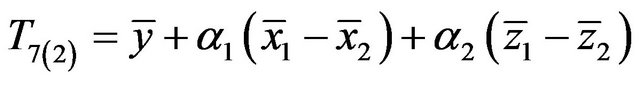(1.14)

(1.15)

where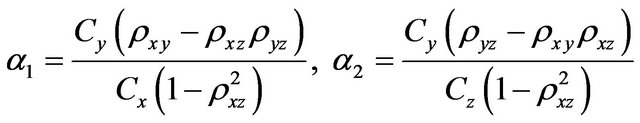

and 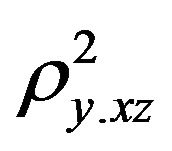is the partial correlation coefficient of given and.

Singh and Espejo [13] extended their own work of single phase sampling ratio-product estimator suggested in (2003) to two-phase sampling.

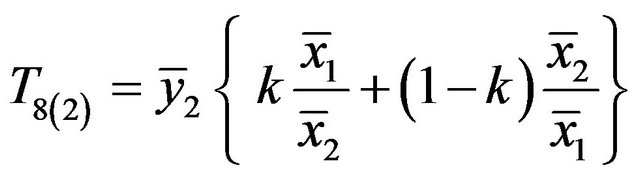, (1.16)

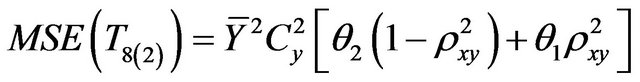(1.17)

where 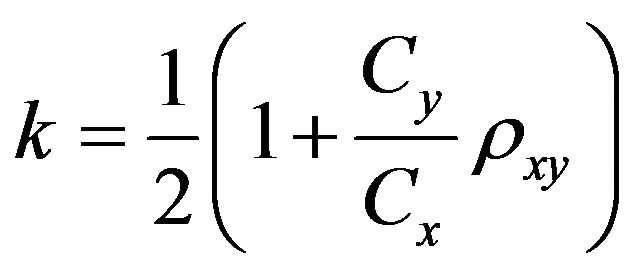and.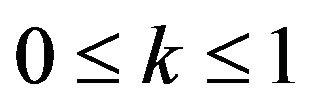

Hanif et al. [14] developed regression type estimators of population mean in two-phase sampling. One of those estimators was:

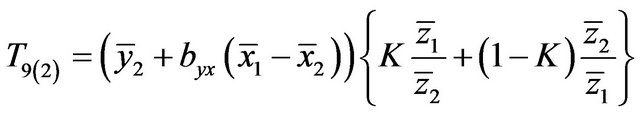, (1.18)

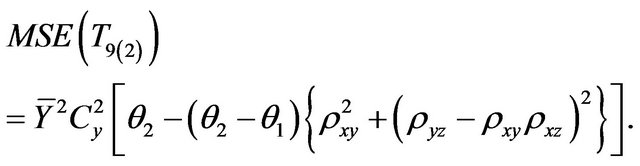(1.19)

2. Proposed Regression Type Estimator for Two-Phase Sampling

We propose following estimator using two auxiliary variables for two-phase sampling when we don’t have any information of auxiliary variables i.e. both 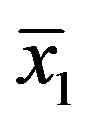and are unknown.

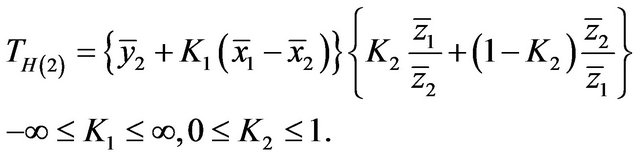(2.1)

Putting the notations of (1.1) in (2.1), squaring and taking expectation, we can obtain mean square as:

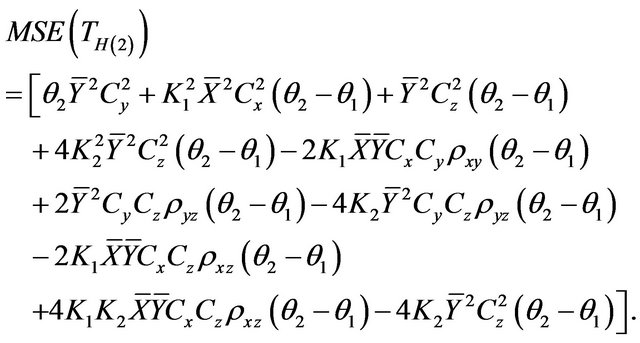
(2.2)

In order to get optimum value of K₁ and K₂ we differentiate (2.2) with respect to K₁ and equating to zero we get:

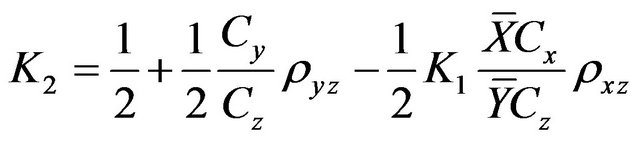. (2.3)

Putting the value of (2.3) in (2.2) and differentiating with respect to K₁, we get:

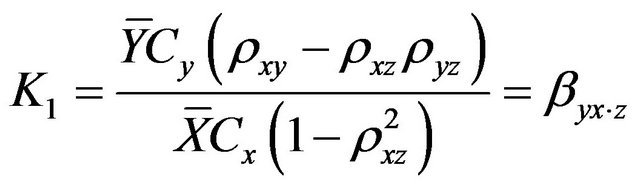(2.4)

where is the partial regression coefficient of y on keeping 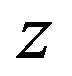constant.

Putting the value of (2.4) in (2.3) we get:

(2.5)

Putting the values of (2.4) and (2.5) in (2.2) and on simplification we have:

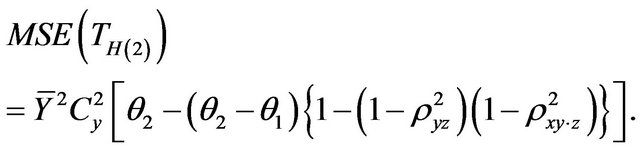(2.6)

Expressing the proposed estimator in terms of (1.1) and taking the assumption that is very small and expanding 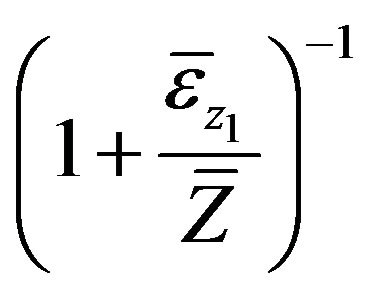and up to second degree, we obtain bias of above estimator as follows

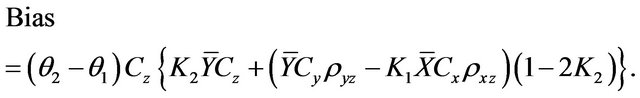
(2.7)

Putting (2.4) and (2.5) in (2.7) and after simplification, the optimized bias is

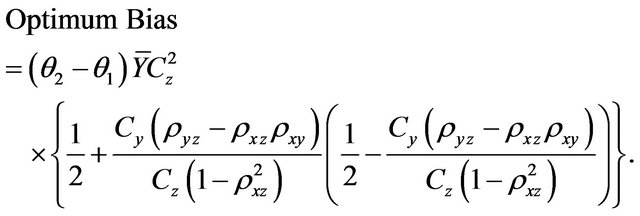
(2.8)

3. Mathematical Comparison of Proposed Estimator over Other Estimators

In this section, an improvement of our proposed estimator is shown over well-known estimators of two-phase sampling. In each case no information about population characteristics of auxiliary variables is available. It is proved through mathematical comparison that our proposed estimator outperforms the other estimators. We have compared our estimator with [3,6-11,13,14] estimators. The mathematical efficiency of our proposed estimator is given as:

a) Comparison with Robson [6] Estimator

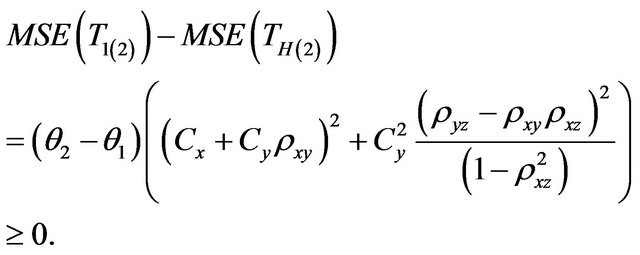(3.1)

b) Comparison with Sukhatme [3] Estimator

(3.2)

c) Comparison with Raj [7] Estimator

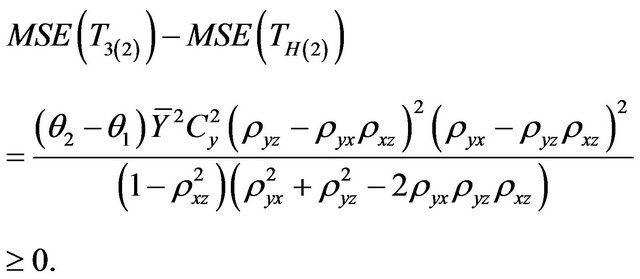(3.3)

d) Comparison with Mohanty [8] Estimator

(3.4)

e) Comparison with Srivastava [9] Estimator

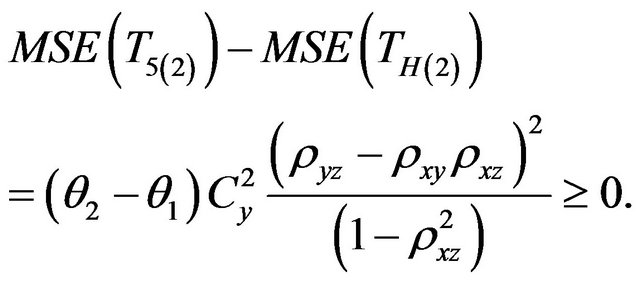(3.5)

f) Comparison with Mukerjee et al. [10] Estimator

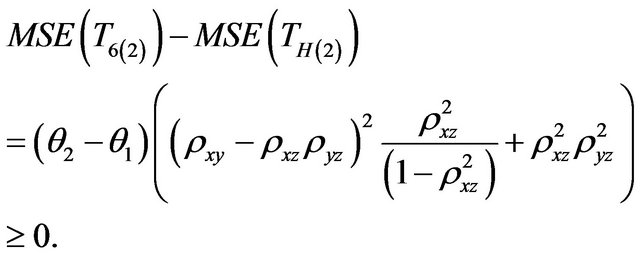(3.6)

g) Comparison with Sammiuddin and Hanif [11] Estimator Our proposed estimator gives identical result to [11] because

(3.7)

But our estimator is more preferable than [11] if we have the estimate of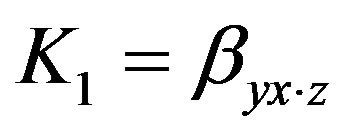, in this way we have to find only one unknown value whereas in [11] estimator we have to find two unknown values. Following special cases give another reason for the suitability of our estimator. Our estimator:

1) becomes classical ratio estimator for and;

2) converts into Robson [6] estimator for 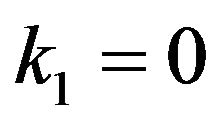and;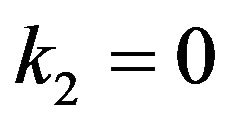

3) emerges into Mohanty [8] estimator for 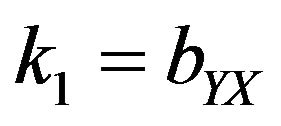and;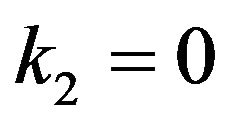

4) reduces to estimator given by Singh and Espejo [13] for;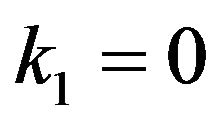

5) turns into Hanif et al. [14] estimator for.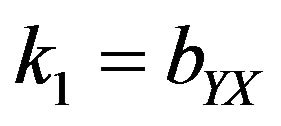

h) Comparison with Singh and Espejo [13] Estimator

(3.8)

i) Comparison with Hanif et al. [4] Estimator

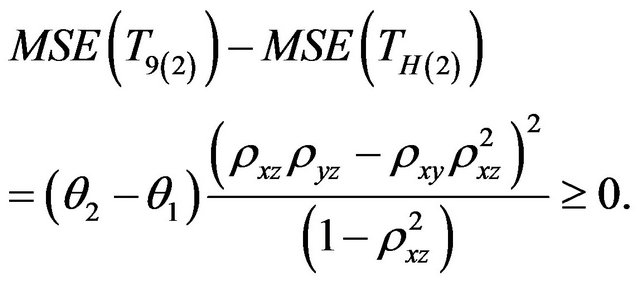(3.9)

4. Conclusion

In this paper we have proposed a regression type estimator for two-phase sampling when we don’t have any advance knowledge of auxiliary variables. [6,8,13,14] are the special cases of our estimator. From Equations (3.1) to (3.9) one can readily see that our proposed estimator is more precise than all other competing estimators discussed in Section 1, so we can say that our estimator provides more accurate estimate about the population parameters.

REFERENCES