Open Journal of Statistics
Vol.2 No.1(2012), Article ID:16880,7 pages DOI:10.4236/ojs.2012.21003
Smoothed Empirical Likelihood Inference for ROC Curves with Missing Data
Department of Mathematics and Statistics, Georgia State University, Atlanta, USA
Email: yan3@student.gsu.edu
Received September 25, 2011; revised November 4, 2011; accepted November 16, 2011
Keywords: Confidence Interval; Missing Data; ROC Curve; Smoothed Empirical Likelihood
ABSTRACT
The receiver operating characteristic (ROC) curve has been widely used in scientific research fields. After using the random hot deck imputation, we propose the smoothed empirical likelihood ratio statistic for the ROC curve with missing data. Its asymptotic distribution is a scaled chi-square distribution and empirical likelihood confidence intervals for ROC curves are constructed. The simulation study shows that the proposed interval estimates perform well based on the coverage probability for different sample sizes and response rates.
1. Introduction
The receiver operating characteristic (ROC) curve has been extensively used to evaluate the diagnostic tests. The ROC curve is usually defined as a graphical plot of the sensitivity vs (1-specificity). It is clear that ROC curve is an appealing method to summarize the accuracy of predictions in the diagnostic test. In recent years, ROC curves have been widely applied to medical research, diagnostic medicine and many other scientific research fields (Zhou, McClish and Obuchowski [1], Pepe [2]).
Empirical likelihood (EL) is a useful nonparametric statistical inference method which does not need to assume a known family of distributions (see Owen [3]). Owen [4,5] originally proposed EL confidence regions for the population mean parameter in the complete data setting. Chen and Hall [6] introduced smoothed EL confidence intervals for quantiles. To improve the performance of normal approximation methods for the ROC curve for small sample sizes, the EL based method has been used to estimate the ROC curve. Claeskens, Jing, Peng and Zhou [7] developed smoothing EL confidence intervals for ROC curves and Su et al. [8] proposed plug-in EL for the ROC curve. Liang and Zhou [9] developed semi-parametric EL confidence intervals for ROC curves with right censoring.
In recent years, missing data problem received much attention in biomedical studies, population survey andmany other related fields. Some of the responses may not be obtained due to information loss (see Qin and Qian [10], Wang and Rao [11]). There is no inference procedure about the ROC curve with missing data. Recently Qin and Qian [10] proposed smoothing EL interval estimation for the difference of two quantiles with missing data. Motivated by their idea, we propose empirical likelihood ratio for the ROC curve with missing data and prove that the resulting EL ratio has a scaled chi-squared limiting distribution. This approach is a natural extension of Claeskens et al. [7] to missing data.
The rest of the paper is organized as follows. In Section 2, adopting Qin and Qian [10]’s approach, which was also from Claeskens et al. [7], we propose the smoothed empirical likelihood ratio statistic, derive its limitingdistribution and construct the empirical likelihood confidence interval for the ROC curve. In Section 3, we conduct a simulation study to evaluate the finite sample performance of the empirical likelihood interval estimation. The conclusion is given in Section 4. The proofs are given in the Appendix.
2. Main Results
In the following, we adopt the same notations and terminologies as those in Qin and Qian [10]. Suppose there are two independent populations 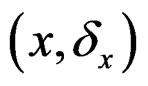 and
and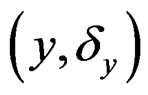 , where
, where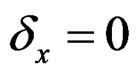 , if x is missing,
, if x is missing, 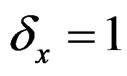 , otherwise;
, otherwise;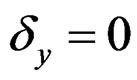 , if y is missing,
, if y is missing, 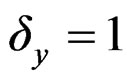 , otherwise. We assume that x, y are missing completely at random, i.e.,
, otherwise. We assume that x, y are missing completely at random, i.e., 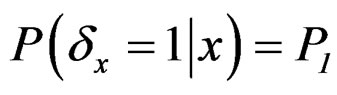 and
and . We consider i.i.d. samples of missing data
. We consider i.i.d. samples of missing data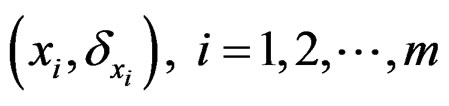 ;
;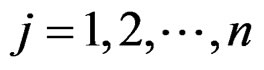
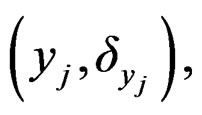 . Let
. Let ,
, 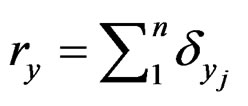 , mx = m – rx and
, mx = m – rx and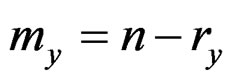 . Qin and Qian [10] use
. Qin and Qian [10] use 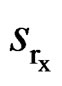 and
and 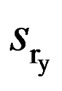 to denote the sets of respondents with respect to x and y, and use
to denote the sets of respondents with respect to x and y, and use 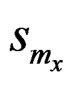 and
and 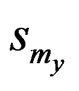 to denote the sets of non-respondents, respectively. Like Qin and Qian [10], we let
to denote the sets of non-respondents, respectively. Like Qin and Qian [10], we let  and
and 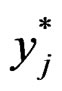 be the imputed values for the missing data with respect to x and y. Use random hot deck imputation to select a
be the imputed values for the missing data with respect to x and y. Use random hot deck imputation to select a  for some
for some 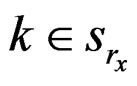 (Little and Rubin [12]). Similarly, we obtain
(Little and Rubin [12]). Similarly, we obtain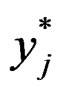 . One can obtain complete data as follows.
. One can obtain complete data as follows.
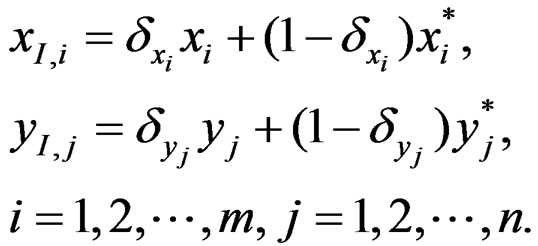
It is of interest to study two populations, one with disease and another one with non-disease. Suppose that the distribution function of disease population X is F(t) and the distribution function of non-disease population Y is G(t). The sensitivity and specificity for a continuous-scale diagnostic test are 1-F(t) and G(t) at a threshold t. At a given level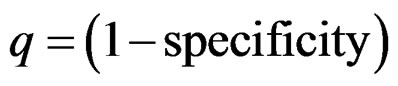 , the ROC curve is expressed as
, the ROC curve is expressed as
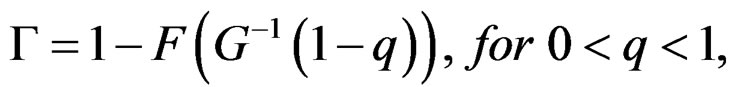
where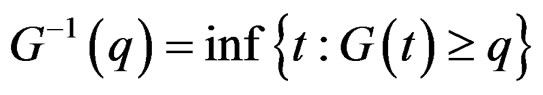 . As Qin and Qian [10], let the bandwidth
. As Qin and Qian [10], let the bandwidth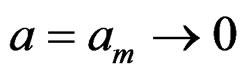 as
as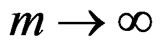 ,
, 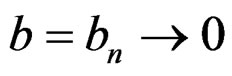 as
as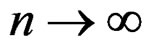 , and the kernel functions
, and the kernel functions 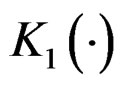 and
and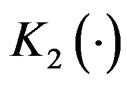 . Define
. Define
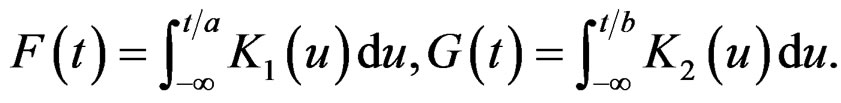
We adopt the smoothed EL approach of Qin and Qian [10] and define the profile EL ratio statistic at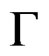 :
:
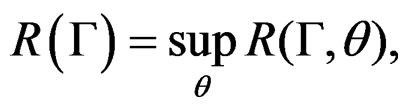
where

and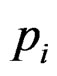 ,
, 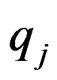 satisfy the following equations:
satisfy the following equations:
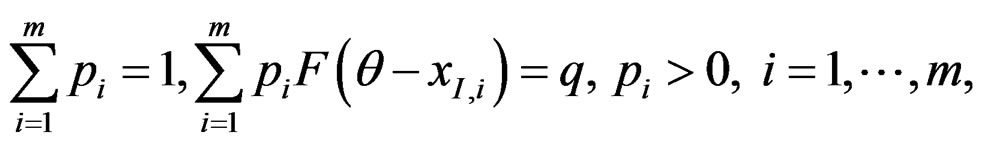

and
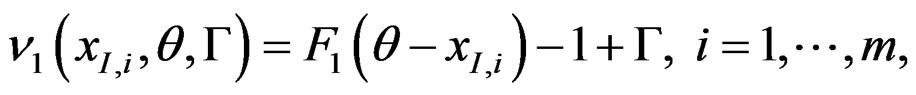

We set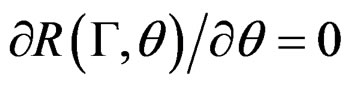 . By using the Lagrange multipliers method, we have that
. By using the Lagrange multipliers method, we have that
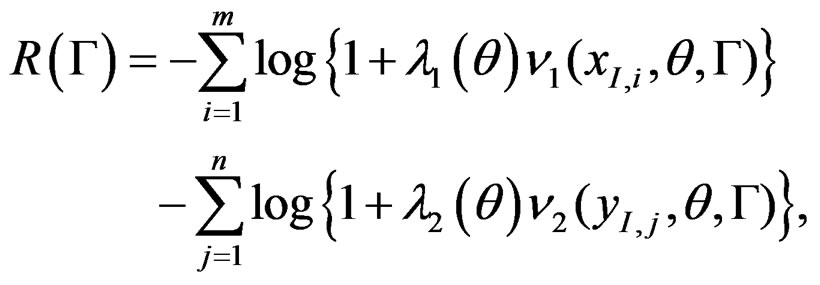
where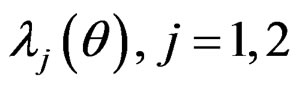 , and
, and 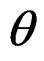 satisfy the following score equations:
satisfy the following score equations:

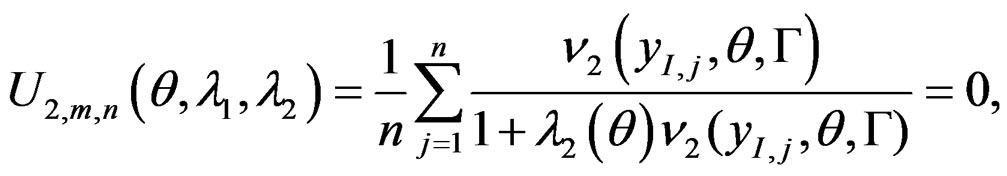
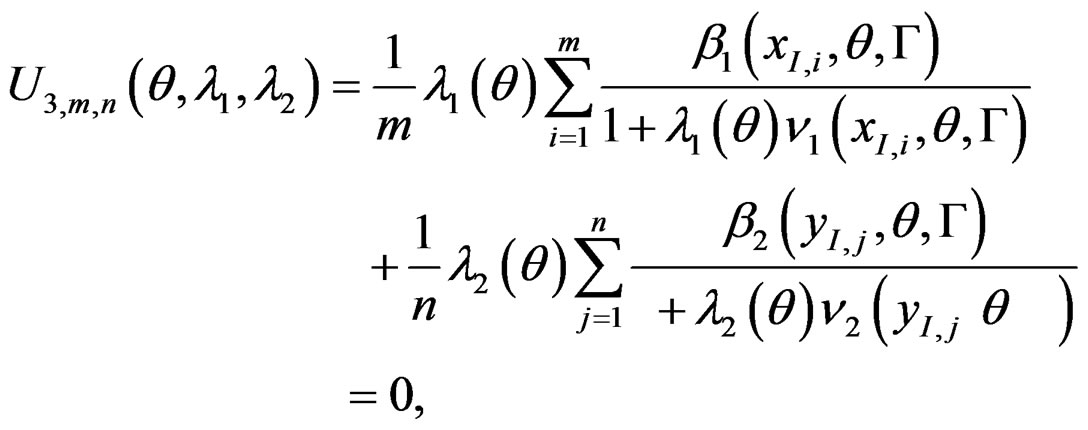
where
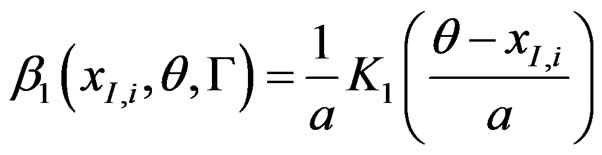
and
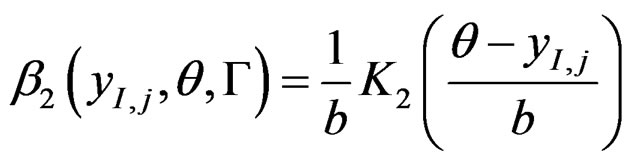 .
.
Suppose that 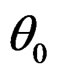 is the true value of
is the true value of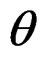 .In this paper, we assume the same regularity conditions (i)-(v) in Qin and Qian [10] with condition (ii) modified as follows:
.In this paper, we assume the same regularity conditions (i)-(v) in Qin and Qian [10] with condition (ii) modified as follows:
(ii) Denote 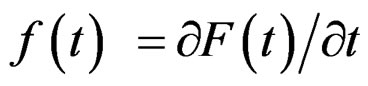 and
and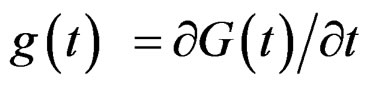 . For some
. For some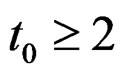 , suppose that
, suppose that 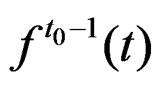 and
and 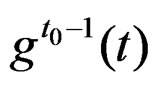 exist and are uniformly continuous and bounded in a neighborhood of
exist and are uniformly continuous and bounded in a neighborhood of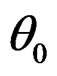 . Assume that
. Assume that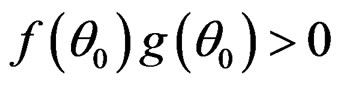 .
.
Recall that condition (iii): n/m → k as m + n → ∞. Then we state the main result about confidence intervals for the ROC curve.
Theorem 1. Under the regularity conditions (i)-(v), as m + n→∞, there exists a root 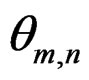 of Equation (1) such that
of Equation (1) such that  attains its local maximum at
attains its local maximum at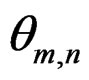 ,
,
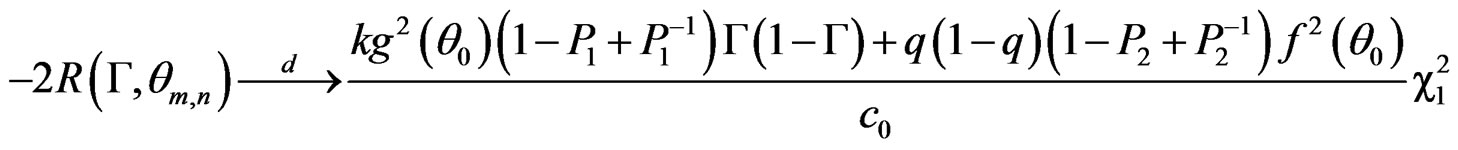
where
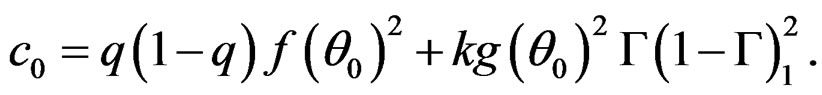
We know that k is estimated by n/m, and  and
and 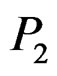 can be consistently estimated by
can be consistently estimated by
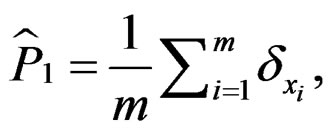
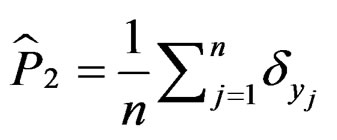
respectively. Qin and Qian [10] showed that,
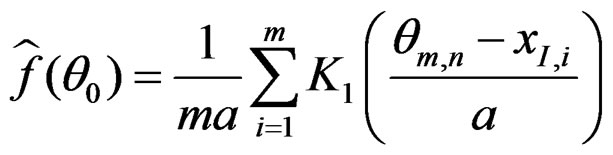
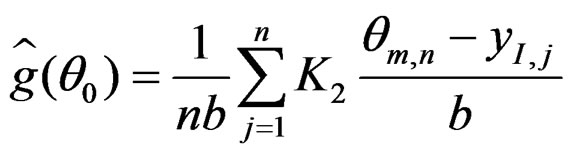
are consistent estimators of  and
and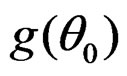 . Put
. Put
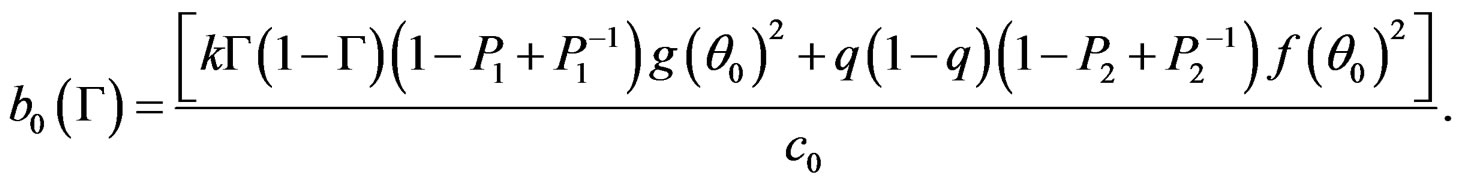
Plugging in the above consistent estimators, we obtain a consistent estimator  of
of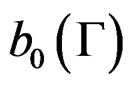 . Let
. Let 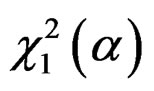 be the upper
be the upper 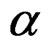 -quantile of
-quantile of . Thus, it follows from Theorem 1 that the
. Thus, it follows from Theorem 1 that the 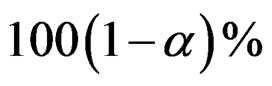 EL confidence interval for
EL confidence interval for  is given by
is given by

Remark: The asymptotic distribution of the EL statistic is a standard 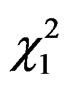 distribution for complete data since
distribution for complete data since 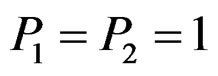 and it coincides with the conclusion of Claeskens et al. (2003).
and it coincides with the conclusion of Claeskens et al. (2003).
3. Simulation Studies
In this section, we carry out extensive simulation studies to evaluate the performance of the EL method for the ROC curve in terms of coverage probability and average length of confidence intervals with different response rates and sample sizes.
The simulation setting is similar to Qin and Qian [10]. The diseased population X is distributed as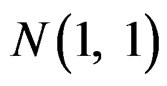 , while the non-diseased population Y follows
, while the non-diseased population Y follows . We choose kernel function
. We choose kernel function
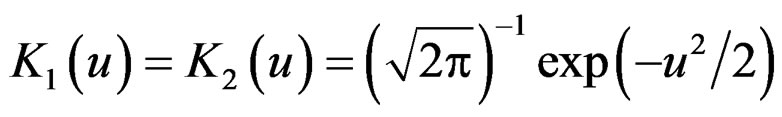
and the bandwidths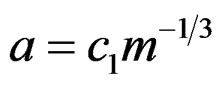 ,
,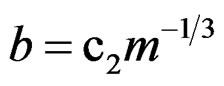 . We draw random samples x and y from the populations X and Y.
. We draw random samples x and y from the populations X and Y.
The response rates for x and y are chosen as 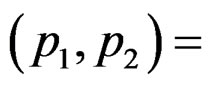
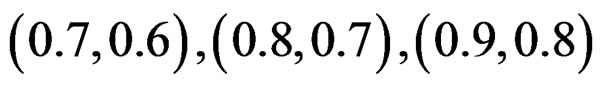 . The sample sizes are chosen to be
. The sample sizes are chosen to be 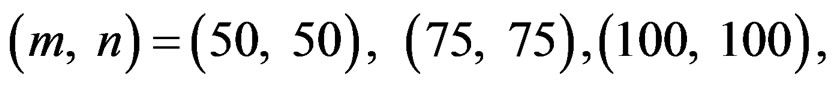
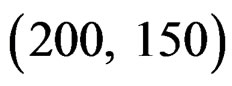 . We generate 1000 random samples of the data. The proposed EL confidence intervals for the ROC curve are constructed at q = 0.1, 0.3, 0.5, and 0.7. The nominal level of the confidence intervals is selected as
. We generate 1000 random samples of the data. The proposed EL confidence intervals for the ROC curve are constructed at q = 0.1, 0.3, 0.5, and 0.7. The nominal level of the confidence intervals is selected as .
.
From Tables 1-4 we have the following findings:
1) Note the response rate is higher and larger than 0.6 in the simulation study. For each fixed response rate and sample size, the coverage probability of confidence intervals for the ROC curve is close to the nominal level 95%. In the simulation, when sample size is small, the coverage probability is still good.
is small, the coverage probability is still good.
2) For almost all the cases in the simulation study, when the response rates increase, the coverage probabilities of confidence intervals are closer to 95%, i.e., they are more accurate, and the average length of the confidence intervals decreases, because larger response rates provide more information for the data.
3) Similarly, when the sample sizes increase, the coverage probabilities of confidence intervals are more accurate, and the average length of the confidence intervals decreases.
4) For different q = 0.1, 0.3, 0.5, and 0.7, the EL confidence intervals maintain good coverage probability, and it is very stable.

Table 1. Empirical likelihood confidence intervals for the ROC curve at 
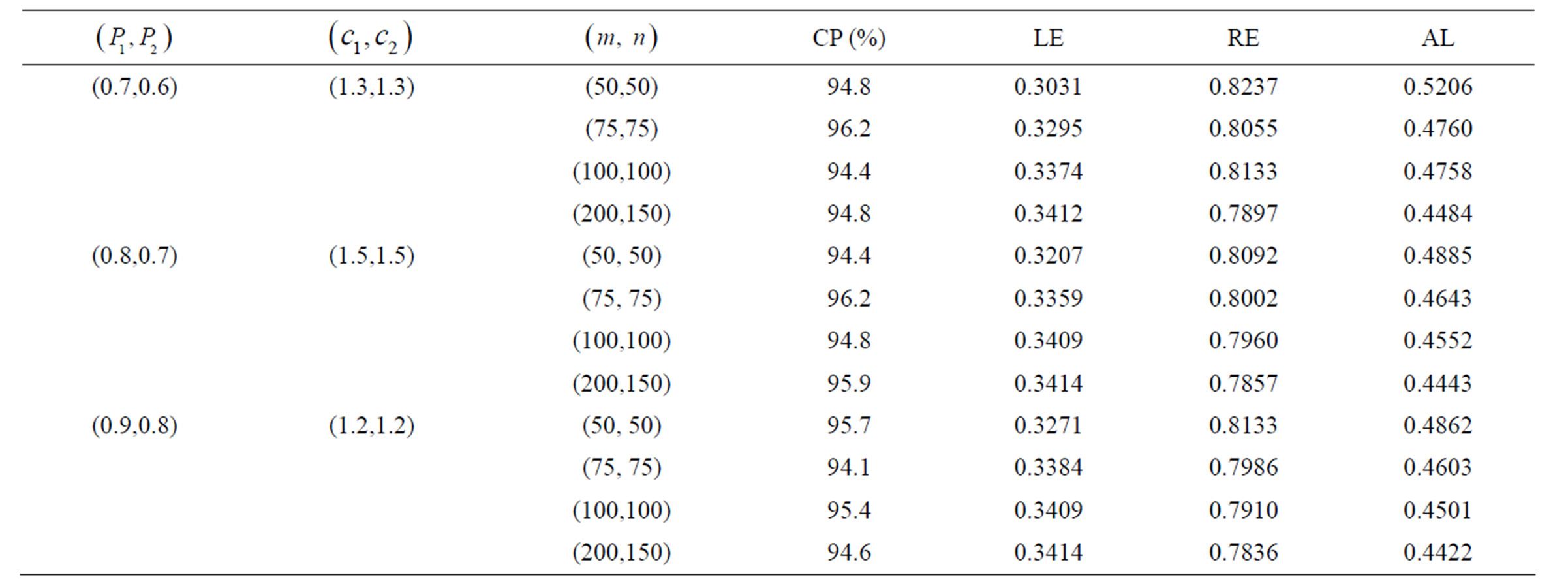
Table 2. Empirical likelihood confidence intervals for the ROC curve at 
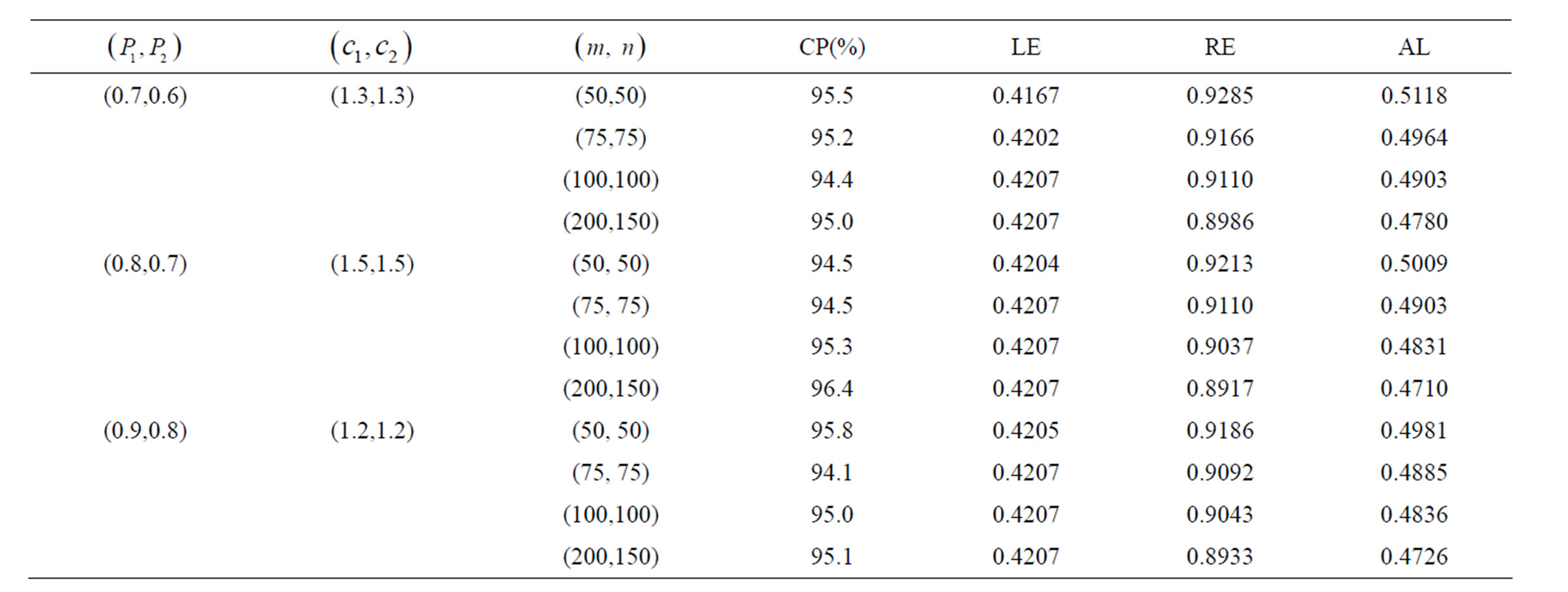
Table 3. Empirical likelihood confidence intervals for the ROC curve at 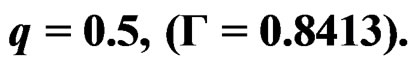
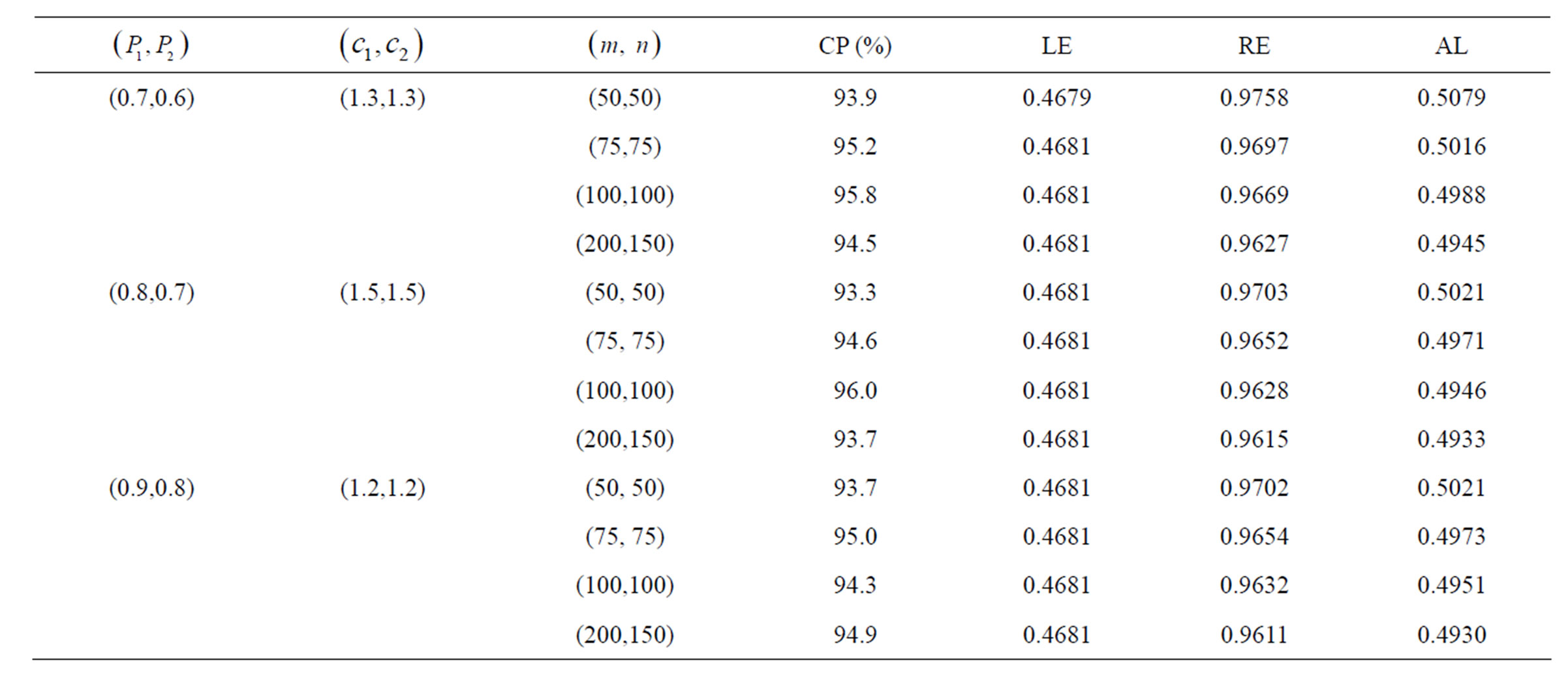
Table 4. Empirical likelihood confidence intervals for the ROC curve at 
4. Discussion
In this paper, we developed the smoothing empirical likelihood method for the ROC curve with missing datawhich is a natural extension of Claeskens et al. [7].The key technique used to impute the missing data is the random hot deck imputation procedure. Under imputation, the proposed smoothed EL statistic converges to a scaled chi-square distribution. In addition, we carry out the simulation studies to evaluate the finite sample performance of the proposed EL interval estimation for the ROC curve. For either smaller or larger q, the EL confidence intervals for the ROC curve have good coverage probabilities which are close to the nominal level. In summary, the proposed EL interval estimation is a reliable and useful tool for the ROC curve analysis with missing data. In the future, we will use other imputation methods to achieve better interval estimation and improve the performance.
5. Acknowledgements
The author acknowledges partial support under a FY09 Research Initiation Grant in Georgia State University. The author would like to thank Dr. Yichuan Zhao for his supervision.
REFERENCES
- X.-H. Zhou, D. K. McClish and N. A. Obuchowski, “Statistical Methods in Diagnostic Medicine,” Wiley, New York, 2002.
- M. S. Pepe, “The Statistical Evaluation of Medical Tests for Classification and Prediction,” Oxford University Press, Oxford, 2003.
- A. B. Owen, “Empirical Likelihood,” Chapman & Hall Ltd, London, 2001. doi:10.1201/9781420036152
- A. B. Owen, “Empirical Likelihood Ratio Confidence Intervals for a Single Functional,” Biometrika, Vol. 75, No. 2, 1988, pp. 237-249. doi:10.1093/biomet/75.2.237
- A. B. Owen, “Empirical Likelihood Ratio Confidence Regions. The Annals of Statistics,” Biometrika, Vol. 18, 1990, pp. 90-120.
- S. X. Chen and P. Hall, “Smoothed Empirical Likelihood Confidence Intervals for Quantiles,” The Annals of Statistics, Vol. 21, No. 3, 1993, pp. 1166-1181. doi:10.1214/aos/1176349256
- G. Claeskens, B.-Y. Jing, L. Peng and W. Zhou, “Empirical Likelihood Confidence Regions for Comparison Distributions and ROC Curves,” The Canadian Journal of Statistics, Vol. 31, 2003, pp. 173-190.
- H. Su, Y. Qin and H. Liang, “Empirical Likelihood-Based Confidence Interval of ROC Curves,” Statistics in Biopharmaceutical Research, Vol. 1, No. 4, 2009, pp. 407- 414. doi:10.1198/sbr.2009.0044
- H. Liang and Y. Zhou, “Semiparametirc Inference for ROC Curves with Censoring,” Scandinavian Journal of Statistics, Vol. 35, No. 2, 2008, pp. 212-227. doi:10.1111/j.1467-9469.2007.00580.x
- Y. S. Qin and Y. J. Qian, “Empirical Likelihood Confidence Intervals for the Differences of Quantiles with Missing Data,” Acta Mathematicae Applicatae Sinica (English Series), Vol. 25, No. 1, 2009, pp. 105-116. doi:10.1007/s10255-006-6116-0
- Q. Wang and J. N. K. Rao, “Empirical Likelihood-Based Inference under for Missing Response Data,” The Annals of Statistics, Vol. 30, No. 3, 2002, pp. 896-924. doi:10.1214/aos/1028674845
- R. J. A. Little and D. B. Rubin, “Statistical Analysis with Missing Data,” 2nd Edition, Wiley & John Sons, New York, 2002.
Appendix. Proof of Theorem 1
To prove Theorem 1, we need some additional lemmassimilar to those in Qin and Qian [10]. We only give an outline of the proofs since they follow similar arguments as Qin and Qian [10].
Lemma A.1. Under the regularity conditions of Theorem 1, as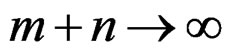 , we have
, we have
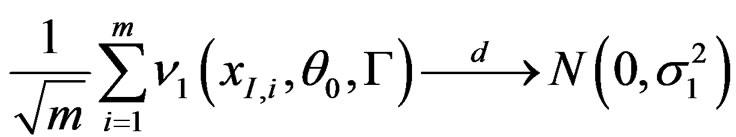
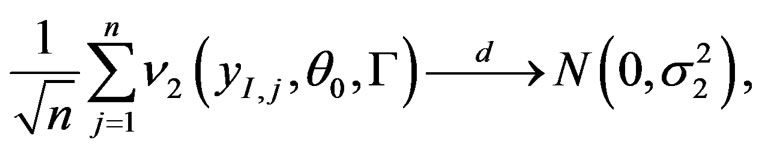
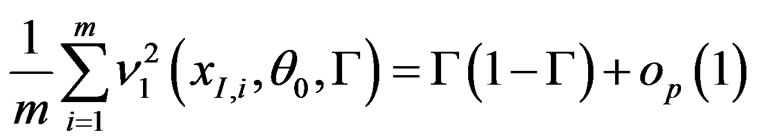
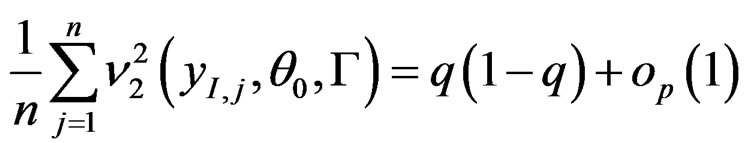
where
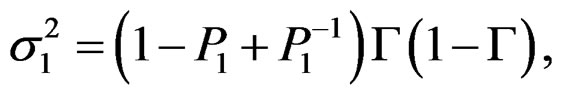
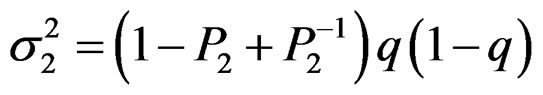 .
.
Proof of Lemma A.1. We follow the similar lines as Qin and Qian [10]. Let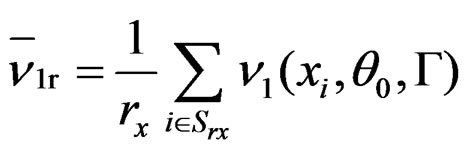 , and
, and . It follows that
. It follows that
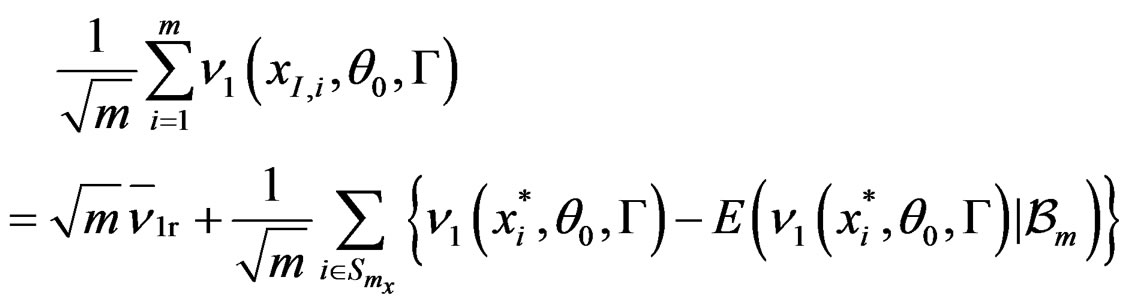
Like Qin and Qian [10], we have that
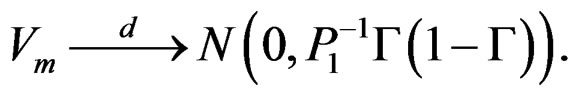
We have

where 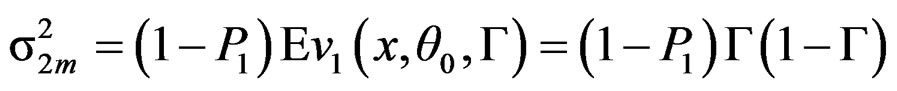 and
and  is the cumulative distribution function of
is the cumulative distribution function of . By Lemma A.1 of Qin and Qian [10], we have
. By Lemma A.1 of Qin and Qian [10], we have
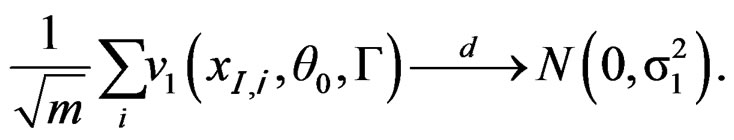
As Qin and Qian [10], we have that,
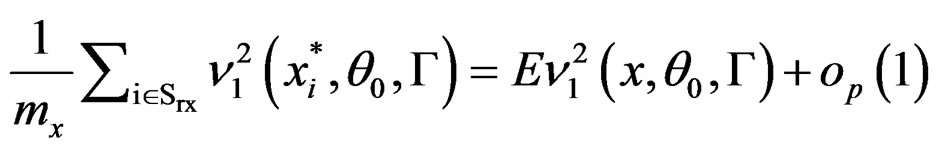

The rest of Lemma A.1 can be proved following same lines. It is omitted.
Lemma A.2. (Qin and Qian [10]). Assume that 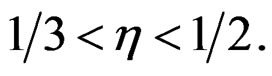 Under the regularity conditions (i)-(v),
Under the regularity conditions (i)-(v),

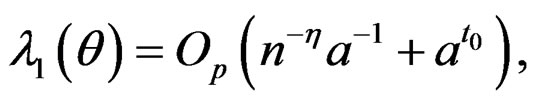
uniformly for 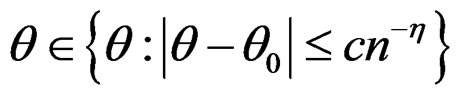 as
as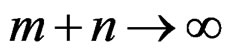 , where c is a positive constant.
, where c is a positive constant.
Proof of Lemma A.2. We follow the same arguments as Qin and Qian [10]. The proof is omitted.
Lemma A.3. (Qin and Qian [10]). Assume that 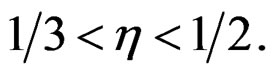 Under the regularity conditions (i)-(v), in probability there exists a root
Under the regularity conditions (i)-(v), in probability there exists a root 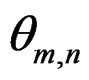 of Equation (1) such that,
of Equation (1) such that,

as , and
, and 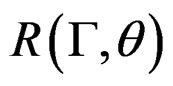 attains its local maximum value at
attains its local maximum value at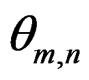 .
.
Proof of Lemma A.3. We follow the similar lines as Qin and Qian [10]. The proof is omitted.
Lemma A.4. Assume that the regularity conditions are satisfied. Then, as 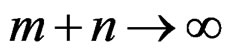
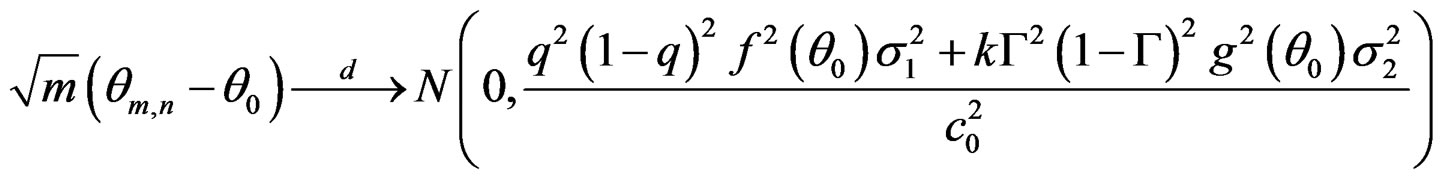
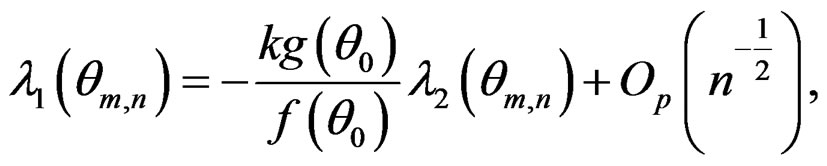
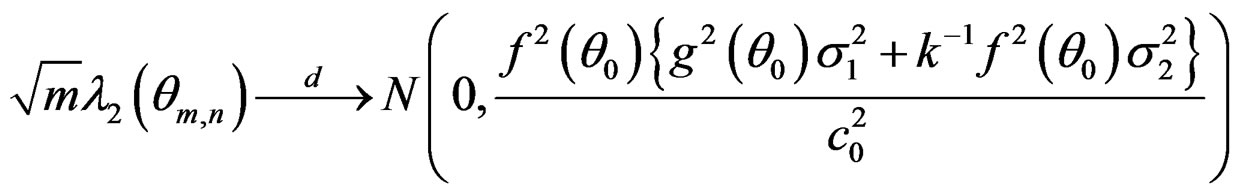
where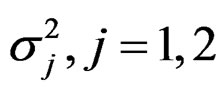 , and c0 are defined in Lemma A.1 and Theorem 1.
, and c0 are defined in Lemma A.1 and Theorem 1.
Proof of Lemma A.4. We follow the similar lines as Qin and Qian [10]. Let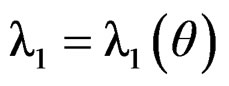 ,
,  ,
,
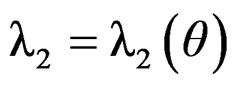 ,
,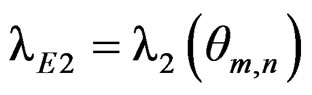 . Using the Taylor expansion, Lemma A.2 and Lemma A.3, we have
. Using the Taylor expansion, Lemma A.2 and Lemma A.3, we have
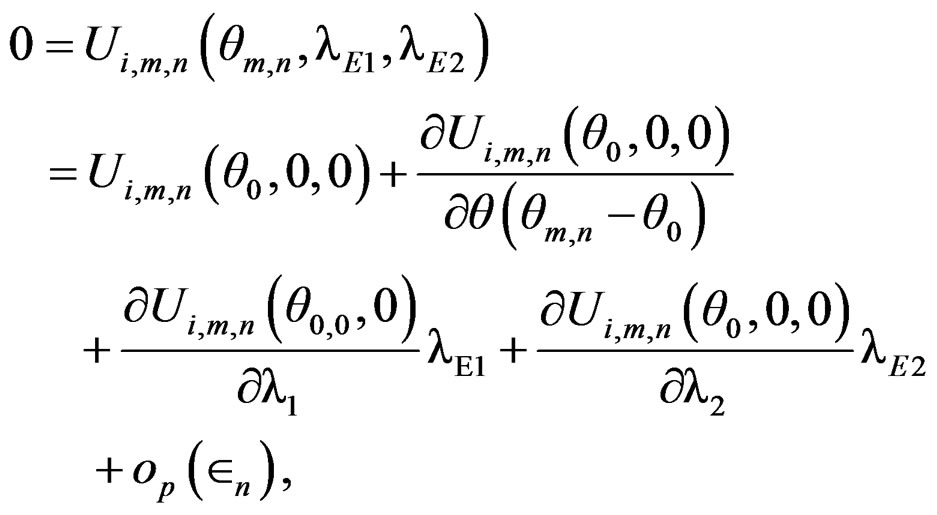
where i = 1, 2, 3,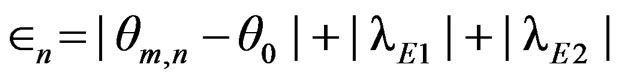 . As Lemma 4.5 of Qin and Qian [10], we can show that
. As Lemma 4.5 of Qin and Qian [10], we can show that
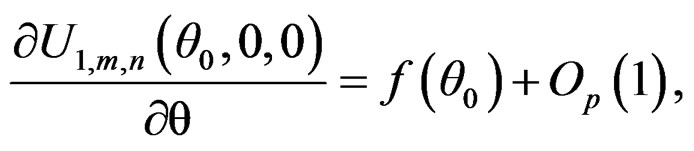
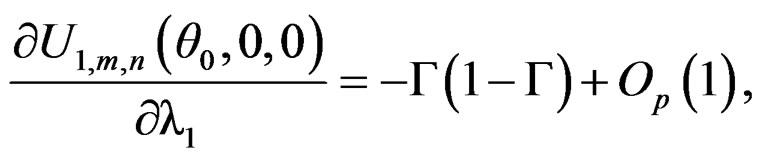
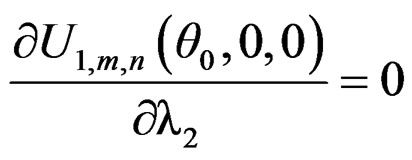

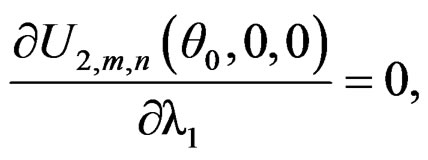

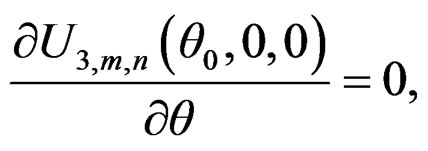

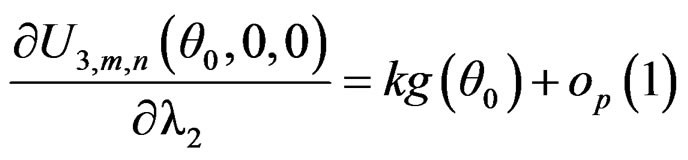
Thus
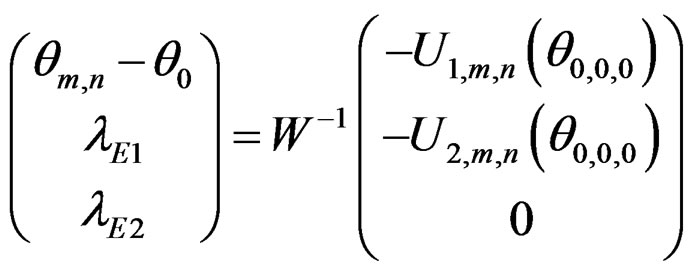
where

It follows that

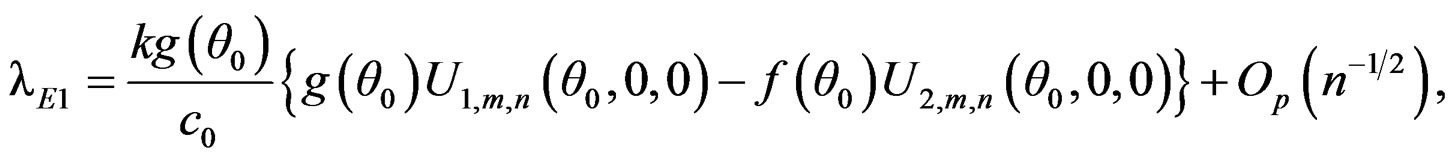
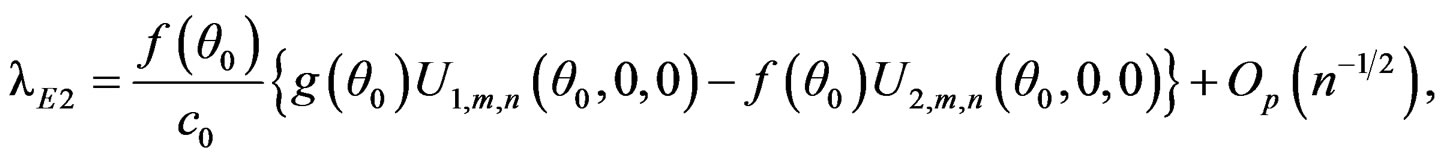
From Lemma A.1, we have

thus Lemma A.4 is proved.
Proof of Theorem 1. It is similar to the proof of Theorem 1 in Qin and Qian [10]. The proof of Theorem 1 is omitted.

