Open Journal of Physical Chemistry
Vol.05 No.04(2015), Article ID:61043,12 pages
10.4236/ojpc.2015.54012
Molecular Dynamics Simulations of Perovskites: The Effect of Potential Function Representation on Equilibrium Structural Properties
Kholmirzo T. Kholmurodov1,2, Sagille A. Ibragimova2, Pavel P. Gladishev2, Anatoly V. Vannikov3, Alexey R. Tameev3, Tatyana Yu. Zelenyak2
1Frank Laboratory of Neutron Physics, JINR, Dubna, Russia
2Dubna International University, Dubna, Russia
3A.N. Frumkin Institute of Physical Chemistry and Electrochemistry, Russian Academy of Sciences, Moscow, Russia

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 26 August 2015; accepted 9 November 2015; published 12 November 2015

ABSTRACT
The perovskites with general formula ABX3 have been widely used as for materials with their unique properties (ferroelectric, piezoelectric, dielectric, catalytic and so on). Hybrid organolead halide perovskites are a class of semiconductors with ABX3 (X = Cl, Br, and I) structures consisting of lead cations in 6-fold coordination (B site), surrounded by an octahedron of halide anions (X site, face centered) together with the organic components in 12-fold cub octahedral coordination. These hybrid perovskites have a direct band gap, a large absorption coefficient as well as high charge carrier mobility that represent a very attractive characteristic of cost-effective solar cells. Basically, these crystals are inorganic solids of CaTiO3 type held together by bonds that are either ionic or partially ionic and partially covalent. In spite of the partially covalent character of the Ti-O bond, the system is modeled by a two-body central force interatomic potential (the form of the Vashishta and Rahman interatomic potential), which has been used successfully for many materials with a perovskite structure. In the present work using molecular dynamics (MD) simulation method we investigate the dynamical and structural behavior of CaTiO3 perovskite at normal pres- sure and temperature conditions. The MD calculations were performed on a system of 16,000 particles (3200Ca + 3200Ti + 96,00O), initially in an orthorhombic-Pbnm structure. The orthorhombic MD box had edges Lx = 53.4 Å, Ly = 53.4 Å and Lz = 61.12 Å, which provided a density matching the experimental value of ρ = 4 g/cm3. Starting with this structure and using proposed interatomic potentials the MD system stabilizes at room temperature in its initial configuration. The aim of the present study to explore the effect of potential function representations on structural equilibrium properties for the perovskite models including hybrid halide ones outlined above. Concerning the perovskite equilibrium state we elucidate the role of potential function modification on the atomic pair correlation and structural re-organization. The details of the interatomic potential representation have to be crucially important for obtaining of correct analysis data in crystallic, liquid and amorphous phases including perovskite systems.
Keywords:
Perovskites, Halides, Potential Functions, Structural Properties, MD Simulations

1. Introduction
The cost effective solar energy production and reproducible device performance are the important subjects in today nanotechnology research. In this respect, computer design and modeling of nanostructures aimed on developing of solar cells prototypes of greater efficiencies represent a great scientific interest. The computer methods based on atomic/molecular modeling approach may provide a lot of useful information concerning the crystal chemistry of solar cell materials, the dynamical and structural data, the thermodynamic properties and phase transitions, charge transfer and diffusion processes, and so on. The computer analysis would obviously be helpful for performing experiments with fewer resources thereby indicating the rationally modifying ways and finding the best structure design for the solar cells materials. In the present article the review of structural characterization of a number solar cell systems together with a novel molecular dynamics (MD) simulation data are presented [1] -[5] .
Organic-inorganic hybrid solar cells. Recently, there are new opportunities for the development of photovoltaics. In 2012-2013 in the field of perovskite semiconductor photovoltaic cells were obtained principally new results for which it was achieved an efficiency of 16%. For today, the efficiency of organic-inorganic hybrid solar elements exceeded up 20% [6] . This relatively new type of photovoltaics has remarkable properties. The roots of these photovoltaic systems lie in the Grätzel’ “liquid” dye-sensitized solar cells (DSSCs). In contrast, the perovskite photovoltaic cells are solid state system with all their advantages. The best results were obtained for the synthetic organic-inorganic perovskite crystals. Organic-inorganic hybrid solar cells that combine mesoporous framework are perovskite light absorber and the electron and hole transporter. Perovskite can be formed as flexible and semi-transparent solar cells. The elements of the perovskite inferior in efficiency while the silicon single-stage and other photoelectric converters, however, have a great advantage in cost and simplicity of manufacture. Some experts are already predicting new material displacement of silicon solar cells [4] -[7] .
Organo-metallic perovskite semiconductor. Organo-metallic perovskite semiconductor structures are attractive because they have high charge carrier mobility and a large diffusion length, allowing the photogenerated electrons and holes effectively to travel long distances without losing energy. As a result, one can use solar cells with more thin layers, which absorb more light and hence, generate more electricity. In this regard, organo-me- tallic, in particular organo-lead perovskite halide solar cells has become one of the most promising candidates for next-generation solar cells [2] -[8] .
Perovskite thin film solar cells. Until recently, the perovskite thin film solar cells have been used exclusively and organic polymeric materials with a relatively low mobility of the holes. In this respect the more promising as a hole conductive materials to use more stable inorganic structures, in particular copper iodide. Hole conductors based on copper previously successfully used in solar cells sensitized with dyes and quantum dots. Copper iodide is inexpensive hole conductive material that can serve as a possible alternative to spiro-OMeTAD. This may lead to the development of inexpensive, high-performance solar cell perovskite. In the future, for such solar cells can be increased voltage and efficiency, in particular by reducing the high rate of recombination. Best efficiency solar cells perovskite already competitive with modern commercial technology at a much lower cost price [1] [5] -[8] .
Further improvement of photovoltaics. Further improvement of such devices is promising the most promising avenue of research in the field of photovoltaics. It is important to carry out a systematic study and optimization of organic-inorganic perovskite structure in order to improve the photoelectric conversion efficiency based on it. These problems will involve the precise calculation methods (as molecular dynamics and related techniques) for exploring the stability effect of substitution known organo-metallic perovskites of different ions to other similar ions. Parallel on the basis of quantum-mechanical calculations the spectral properties of various perovskite systems could be predicted. These results have to bring to determination and identification of the most stable crystal structures with the necessary spectral, photovoltaics, and other properties important for photoelectric conversion.
Stability of developed new perovskite solar cells. The formation of perovskite thin film photovoltaic cells with high efficiency involves their further studies from the point of view of the radiation and thermal stabilities. One believes that for the newly developed perovskite solar cells the problems of radiation damages will be on the top of the structural, spectroscopic and other physical methods research as future trends.
2. The Perovskites Structure Properties and Design Aspects
Understanding the basic properties and functioning of organo-metallic perovskites solar cells represent a great scientific and technological interest due to a number of their unique properties (ferroelectric, piezoelectric, dielectric, catalytic and so on). The radiation and thermal stability of perovskite developed solar cells in this respect are the problems of a great research interest as well. Synthesis of new optimal perovskite semiconductor systems inevitably demands the studies of their spectral, structural and photovoltaic properties. The formation of new organic-inorganic perovskite solar cells of high efficiency characteristics correlate with the theoretical research investigation. So far, the development of theoretical and computational methods, as like as molecular dynamics and quantum chemical calculations, are important issues for the search of optimizing perovskite structures, studying the melting and phase transitions, diffusion and conductivity phenomena, etc., that are aimed on the innovation of new photovoltaic systems unknown for today [1] [4] [9] . In the present study we have performed molecular dynamics (MD) simulation on CaTiO3 system as a basic perovskite structure. The above mentioned system represents the most studied perovskite model. We have been aimed to compare the structural behavior of the CaTiO3 perovskite under different intermolecular potential representations. Such analysis and comparison between different simulation approaches allow one to extend the studies on more complicated perovskite structures (as like as hybrid organolead ones) on stronger motivated basis.
The perovskites with general formula ABO3 have been widely used for crystal materials. A typical representative of the class of modern crystal materials known as perovskites is calcium-titanate (CaTiO3) The perovskite CaTiO3 is feroelastic with an orthorhombic symmetry at room temperature (space group Pbnm) and undergoes two phases transitions at respectively T1~1398 K (space group Mmcm) and T2~1523 K (space group Pm3m). CaTiO3 can be prepared by the combination of CaO and TiO2 at temperatures >1300˚C. The sol-gel processes have been used to make a more pure substance, as well as lowering the synthesis temperature. These compounds synthesized are more compressible due to the powders from the sol-gel process as well and bring it closer to its calculated density (~4.04 g∙mol−1). Below in Figure 1 several typical perovskite structures are shown.
Another group of metallo-organic perovskites is a system of type CH3NH3PbХ3. For example, [CH3NH3]+Pb2+Х3, perovskite of mixed halide form, methylammonium lead iodide. For the above system, X represents halogens (Br or I), halogen mixes (CH3NH3PbI3−xClx) or more complicated one, (R(CH2)2NH3)2PbХ4, with R as phenyl or halogen derivatives (see Figure 2).
In the basic structure, CaTiO3 (Ca2+, Ti4+, O2−), or general representation ABX3, alkali atoms occupy A sites, A (Cs, Rb, CH3NH3), Pb atoms occupy B sites, B (Pb), and halogen atoms occupy X sites, X (Cl, Br, I). In this regard, the perovskite system of Cs+Pb2+F− type represents the most interesting object. We emphasize the modern trend in developing of more complicate perovskites as [Me NH3]+Pb2+F−, [Rn NH3]+Pb2+F− (n > 1), [RnRmNH3]+Pb2+F−, [RnRmRkNH]+Pb2+F−, [RnRmRkRlN]+Pb2+F− with halogens F− = (F−, Cl−, Br−, I−). Figure 3 demonstrates schematic aspects of the perovskite structure models.
Basically, hybrid organolead perovskites are inorganic solids of CaTiO3 type structure held together by the ionic or partially ionic and partially covalent bonds. In spite of the partially covalent character of the Ti-O bond, the system is modeled by a two-body central force interatomic potential, which has been used successfully for many ceramics materials of hybrid halide perovskites type. In the present work a series of the MD simulations were performed to investigate the effect of potential function representations on structural equilibrium properties for the CaTiO3 model structure possessing similar behavior as hybrid halides and other complicated perovskites [3] -[10] .
3. The MD Simulation and Interaction Potential
The MD calculations were performed on a system of 16,000 particles (3200Ca + 3200Ti + 9600O), initially in
Figure 1. Several typical perovskite structures with a chemical formula ABX3 are shown. The red spheres are X atoms (usually oxygens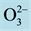 ), the blue spheres are B-atoms (a smaller metal cation, such as Ti4+), and the green spheres are the A-atoms (a larger metal cation, such as Ca2+). (Refs: A public domain of the World Wide Web and https://en.wikipedia.org/wiki/Perovskite_(structure)).
), the blue spheres are B-atoms (a smaller metal cation, such as Ti4+), and the green spheres are the A-atoms (a larger metal cation, such as Ca2+). (Refs: A public domain of the World Wide Web and https://en.wikipedia.org/wiki/Perovskite_(structure)).
Figure 2. The structure of perovskite of mixed halide form, methylammonium lead iodide [CH3NH3]+Pb2+Х3 (Refs: A public domain of the World Wide Web).
Figure 3. The structure representation of more complicate perovskite system.
an orthorhombic Pbnm structure. The structure was built using the data base of Institute of Experimental Mineralogy of Russian Academy of Sciences, http://database.iem.ac.ru/mincryst (Card No: 3594, PEROVSKITE CaTiO(3), Orthorhombic Pbnm, Z = 4; Ref.: Wyckoff R.W.G. (1963), Crystal Structures, 2, 410). The lattice parameters were as: a = 5.37 Å, alpha = 90o; b = 5.44 Å, beta = 90o; c = 7.64 Å, gamma = 90˚; unit cell volume = 223.19 Å3; molar volume = 33.61 cm3/mol.
Table 1 and Table 2 demonstrate the atomic position details of the perovskite CaTiO3 structure model.
The orthorhombic MD box had edges Lx = 53.4 Å, Ly = 53.4 Å and Lz = 61.12 Å, which provided a density matching experimental value of ρ = 4.0 g∙cm−3 as in work [1] . (Comparing with [1] where the MD parameters were used for a system of 10,240 particles = 2048Ca + 2048Ti + 6144O of an orthorhombic-Pbnm structure within the box Lx = 43.022 Å, Ly = 43.494Å and Lz = 61.107 Å, providing the density ρ = 4 g/cm3). Starting with the initial structure as described above and using the proposed interatomic potential, the MD system stabilizes at room temperature in the relaxed configuration. The MD simulation have been performed on the basis of the DL_POLY general-purpose code [11] [12] . Various combinations of the integration algorithm were used
Table 1. Co-ordinates, thermal parameters, occupation for atomic positions.
Table 2. Co-ordinates for all atomic positions.
(NPT and NVT ensembles) controlling the pressure/temperature of the system with the standard termostat and barostat relaxation procedures (see, Appendices 1 and 2 for the FIELD and CONTROL files).
It should be noted that perovskite crystals are inorganic solids held together by bonds that are either ionic or partially ionic and partially covalent [1] . In spite of the partially covalent character of the Ti-O bond, the system is modeled by a two-body central force interatomic potential, based on the form of the Vashishta and Rahman (VR) interatomic potential, which has been used successfully for many different systems. The total potential energy of the system is written as ([1] , see also Figure 4 [1] ):
The first term in the above formula is the Coulomb interaction potential between the ions Zi, Zj (in units of the electron charge |e|), rij = ri − rj is he interatomic distance between ions i and j, and λ is the screening length for the Coulombic interactions. The second term represents the steric effects of the ions sizes, where Hij and ηij are the strength and exponent of steric repulsion, respectively (in [1] the following values were used ηij = 11 (for Ca-Ca and Ti-Ti pairs), 9 (for Ca-Ti, Ca-O and Ti-O), and 7 (for O-O)). The third term represents the charge-induced dipole interaction, to include the electronic polarizabilities of the atoms, where Dij is the strength of the charge-dipole attraction (O2− is a highly polarizable ion). The last is the induced dipole-dipole potential
Figure 4. Two-body interaction potential as a function of distance. The total interaction potential is the sum of all two-body potentials [1] .
based on the van der Waals interaction, where Wij is its strength. Parameter ξ is the screening length for charge- dipole interactions, respectively.
We neglect both screening terms for the Coulombic (i.e. exp(−r/λ) = 1) and charge-dipole (ξ → 0) interactions. Also for the ions steric repulsion we consider a fixed value ηij = 12 for all interacting atomic pairs. In such approximation the above mentioned VR interatomic potential approximates the well-know Lennard-Jones (LJ) or (12 - 6) potential types that are being widely used for the MD simulations of the condensed molecular systems similar to perovskites [12] -[16] :
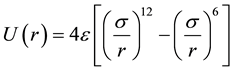 ,
,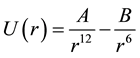 .
.
Table 3 and Table 4 show the atomic and potential parameters of the perovskite CaTiO3 model.
4. Result and Discussion
Configuration snapshots. In Figure 5 and Figure 6 we present the computer generated CaTiO3 perovskite structures at initial and relaxed (equilibrium) states. During the equilibrization the sample structure undergoes the recrystallization modification due to the cooling and melting processes. It is well know that in the single crystal the recrystallization occurs in the orthorhombic structure though the amorphous regions to be formed during the relaxation procedure. The present results obtained by present MD calculations agree with the simulation and experimental reported for the polycrystalline material similar to CaTiO3 perovskite structure [1] .
Pair distribution functions. The MD simulation results for the RDF (radial distribution function) gαβ(r) are summarized in the Figures 7-10. For the comparison we also present the results reported in [1] and obtained by the VR potential. In Figure 7. the graphs of RDF (radial distribution function) gαβ(r) vs. r are presented for the ionic pair Ca-Ca: (a) 12 - 6 potential and (b) VR potential [1] . The comparison indicate a similar RDF behave for both 12 - 6 and VR potentials. We see existing of the three largest gαβ(r) peaks for both (a) and (b) models. However, for the 12 - 6 potential the position of the gαβ(r) peaks are located closer to the origin of r axis. This means that the Ca-Ca ionic pair forms in 12 - 6 model relatively stronger bond than in the VR model. In Figure 8. the RDF graphs are presented for the ionic pair Ca-O. The comparison with the MD results of [1] indicate that the location of the gαβ(r) peak for both 12 - 6 and VR potentials are very close to each other. However, for the 12 - 6 potential we observe a very large gαβ(r) peak (the value of the gαβ(r) peak in model (a) is four times larger than in model (b)). This implies for the Ca-O a stronger ordering and ionic pair correlation for 12 - 6
Table 3. The atomic masses and charges of the perovskite system CaTiO3.
Table 4. Parameters of the two-body interaction potential used in the MD simulations.

Figure 5. Computer generated perovskite structures are shown for the CaTiO3 ((a): top view, (b): side view). The red spheres are oxygens (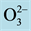 ), the smaller green spheres are metal cation Ti4+, the larger blue spheres are metal cation Ca2+.
), the smaller green spheres are metal cation Ti4+, the larger blue spheres are metal cation Ca2+.

Figure 6. Computer generated two relaxed configurations of the CaTiO3 perovskite structure are shown. The red spheres are oxygens (
Figure 7. The RDF (radial distribution function) gαβ(r) vs. r for the ionic pair Ca-Ca from the MD simulations at T = 300 K obtained by (a) 12 - 6 potential and (b) VR potential [1] .
Figure 8. The RDF (radial distribution function) gαβ(r) vs. r for the ionic pair Ca-O from the MD simulations at T = 300 K obtained by (a) 12 - 6 potential and (b) VR potential [1] .
Figure 9. The RDF (radial distribution function) gαβ(r) vs. r for the ionic pair O-O from the MD simulations at T = 300 K obtained by (a) 12 - 6 potential and (b) VR potential [1] .
potential comparing to the VR one. In Figure 9 the RDF graphs are shown for the ionic pair O-O. The comparison of the left and right hand-side graphs indicate that the amplitudes of the gαβ(r) for both 12 - 6 and VR potentials are not so much differ from each other.Though even in (a) 12 - 6 model a secondary gαβ(r) peak seem to appear which does not exist in the (b) VR poteitial model. Thus, for the O-O pair interactions negleting the Coulombic and charge-dipole screening potentail terms do not effect O-O ordering even so the O2− is a highly polarizable ion. In Figure 10 the RDF graphs are shown for the ionic pair Ti-Ti. The results show that the Ti-Ti ordering and interaction for the (a) 12 - 6 potential visibly are weakened in comparison with the (b) VR potential.
Figure 10. The RDF (radial distribution function) gαβ(r) vs. r for the ionic pair Ti-Ti from the MD simulations at T = 300 K obtained by (a) 12 - 6 potential and (b) VR potential [1] .
5. Conclusion
The paper is aimed on molecular-dynamics (MD) simulation of the CaTiO3 perovskite model concerning the effect of interatomic potential function modification on the relaxed equilibrium states. The proposed earlier in [8] the Vashishta and Rahman (VR) interatomic potential has shown to successfully work for many different systems including perovskites. In [1] the VR interaction potential was used for the MD simulation of CaTiO3 system and it was proved that the VR potential to be very effective for the describing of structural phase transitions under the temperature change; the MD results obtained in [1] were the same as in experimental observations. In the present study work we have made modification of the VR potential, neglecting both screening terms for the Coulombic (i.e. exp(−r/λ) = 1) and charge-dipole (ξ → 0) interactions, thereby approaching the VR potential to the well-know Lennard-Jones (LJ) or (12 - 6) ones. With such modifications the MD generated configuration snapshot remain similar to existing experimental and simulation observations. Nevertheless, the behavior of the RDF (radial distribution function) gαβ(r) undergoes essential changes. For the ionic pair Ca-Ca the comparison indicate a similar RDF behave for both 12 - 6 and VR potentials, showing existing of three largest gαβ(r) peaks, but for the 12 - 6 potential the position of the gαβ(r) peaks are located closer to the origin of r axis. For the ionic pair Ca-O the gαβ(r) peak for both 12 - 6 and VR potentials are very close to each other, but for the 12 - 6 potential we observe a very large gαβ(r) peak where the value of the gαβ(r) in (12 - 6) model has to be four times larger than in VR model. That just implies the Ca-O stronger ordering and ionic pair correlation for 12-6 potential comparing to the VR one. On the contrary, for the ionic pair O-O the gαβ(r) for both 12 - 6 and VR potentials are not so much differ from each other, implying that for the O-O pair interactions negleting the Coulombic and charge-dipole screening potentail terms do not effect O-O ordering even so the O2− is a highly polarizable ion. Also for the ionic pair Ti-Ti our MD results indicate that the Ti-Ti ordering and interaction for the (12 - 6) potential have to weaken in comparison with the VR potential. In conclusion, the details of the atomic pair re-organization due to interatomic potential modifications elucidate on the role of potential function representation for cystallic, liquid and amorphous phases including the perovskite systems.
Acknowledgements
The authors acknowledge the financial support from RFBR (Russian Foundation for Basic Research), grant No. 14-43-03544 (the research ideas and calculation schemes for studies organic-inorganic perovskites crystallic structures) and RSCF (Russian SCience Foundation), grant No. 15-13-00170 (the performance of molecular- dynamics research for organic-inorganic perovskites of Pbnm structure type and generalization of the results).
Cite this paper
Kholmirzo T.Kholmurodov,Sagille A.Ibragimova,Pavel P.Gladishev,Anatoly V.Vannikov,Alexey R.Tameev,Tatyana Yu.Zelenyak, (2015) Molecular Dynamics Simulations of Perovskites: The Effect of Potential Function Representation on Equilibrium Structural Properties. Open Journal of Physical Chemistry,05,110-121. doi: 10.4236/ojpc.2015.54012
References
- 1. Souza, J.A. and Rino, J.P. (2011) A Molecular Dynamics Study of Structural and Dynamical Correlations of CaTiO3. Acta Materialia, 59, 1409-1423.
http://dx.doi.org/10.1016/j.actamat.2010.11.003 - 2. Taibi-Benziada, L., Mezroua, A. and Von Der Mühll, R. (2004) CaTiO3 Related Materials for Resonators. Ceramics-Silikáty, 48, 180-184.
- 3. Calleja, M., Dove, M.T. and Salje, E.K.H. (2003) Trapping of Oxygen Vacancies on Twin Walls of CaTiO3: A Computer Simulation Study. Journal of Phyics: Condensed Matter, 15, 2301-2307.
- 4. Cai, B., Xing, Y.D., Yang, Z., Zhang, W.-H. and Qiu, J.S. (2013) High Performance Hybrid Solar Cells Sensitized by Organolead Halide Perovskitest. Energy & Environmental Science, 6, 1480.
- 5. Haruyama, J., Sodeyama, K., Han, L.Y. and Tateyama, Y. (2014) Termination Dependence of Tetragonal CH3NH3PbI3 Surfaces for Perovskite Solar Cells. Journal of Physical Chemistry Letters, 5, 2903-2909.
- 6. Jishi, R.A., Ta, O.B. and Sharif, A.A. (2014) Modeling of Lead Halide Perovskites for Photovoltaic Applications. Journal of Physical Chemistry C, 118, 28344-28349.
http://dx.doi.org/10.1021/jp5050145 - 7. Mashiyama, H., Kawamura, Y., Kasano, H., Asahi, T., Noda, Y. and Kimura, H. (2007) Disordered Configuration of Methylammonium of CH3NH3PbBr3. Determined by Single Crystal Neutron Diffractometry, Ferroelectrics, 348, 182-186.
http://dx.doi.org/10.1080/00150190701196435 - 8. Vashishta, P. and Rahman, A. (1978) Ionic Motion in α-AgI. Physical Review Letters, 40, 1337-1340.
- 9. Voronov, V.N. (2006) Ion Mobility and Properties of Perovskite ABX3 Type Systems. Preprint № 000F. Physics Institute SB RAS, Krasnoyarsk, 64 p.
http://test.kirensky.ru/zdoc/vvn_preprint.pdf - 10. Razumov, V.F. and Klyuev, M.V., Eds. (2015) Organic and Hybrid Nanomaterials: Synthesis and Application Aspects: Monograph. Ivanovo State University, Ivanovo, 426-556.
- 11. Smith, W. and Forester, T.R. (1996) DL_POLY_2.0: A General-Purpose Parallel Molecular Dynamics Simulation Package. Journal of Molecular Graphics, 14, 136-141.
- 12. Smith, W., Forester, T.R. and Todorov, I.T. (2008) The DL POLY 2 User Manual. STFC Daresbury Laboratory Daresbury, Warrington, Version 2.19.
- 13. Kholmurodov, K., Ed. (2007) Molecular Simulation Studies in Material and Biological Sciences. International Workshop. Nova Science Publishers Ltd., New York, 196 p.
- 14. Kholmurodov, K., Ed. (2009) Molecular Simulation in Material and Biological Research. Nova Science Publishers Ltd., New York, 155 p.
- 15. Kholmurodov, K., Ed. (2011) Molecular Dynamics of Nanobistructures. Nova Science Publishers Ltd., New York, 210 p.
- 16. Kholmurodov, K., Ed. (2013) Models in Bioscience and Materials Research: Molecular Dynamics and Related Techniques. Nova Science Publishers Ltd., New York, 208 p.
Appendix A
Appendix B














