Received 21 August 2014; revised 18 September 2014; accepted 14 October 2014

ABSTRACT

On the example of typical metals, it’s found that the activation energy of self-diffusion is above of the melting heat and below of vaporization heat. This corresponds to the existence of liquid-mo- bile particle classification based on the concept of randomized particles. A formula for estimating the activation energy of self-diffusion by which it is approximately half of the heat of evaporation of the substance is recommended. We derive the temperature dependence for a fraction self-diffu- sion’s particles.

Keywords:

Heat of Fusion, Heat of Boiling, Self-Diffusion, Randomized Particles, Metals

1. Introduction

Thermal state of matter is described by the Boltzmann’s distribution for the kinetic energy of the random motion of particles with energy levels from zero to infinite. In this connection it is of interest to determine the location of the self-diffusion particles in the modern graduation randomized particles energy responsible for the stabiliza- tion of solid, liquid and gaseous states of matter.

Data on self-diffusion activation energy are used for the analysis of plastic deformation in order to support optimum temperature for heating billet rolling mills. However, until now it was not possible to determine the proportion of particles capable to overcome the energy barrier of the self-diffusion, i.e. virtual (reversible) out- put from the crystal lattice. This feature provides a concept of randomized particles through a clear delineation of these particles on the energy barriers melting and boiling points. In connection with this research objective, it was to establish affiliation self-diffusion particles to one of three classes of randomized particles-crystal-mobile, liquid-mobile and vapor-mobile, determine the absolute share self-diffusion particles in accordance with the general classification of randomized particles. To this end, enough data are extensively used on the thermal cha- racteristics of typical metals, for which they have the most important theoretical and practical significance.

2. The Calculation Part

The aforementioned characteristics of simple substances, as well as their melting point and boiling point are presented in Reference [1] , which are taken from data for the typical metal in the presence of all these characte- ristics (Table 1).

As can be seen from the data, for a variety of metals with melting points from 429 to 3653 K and the boiling point of 1180 to 5640 K, with a heat of melting of from 2.81 to 35.30 kJ/mol, and the boiling heat of 99.6 to 770.18 kJ/mol activation energy for self-diffusion is above heat of melting and below the heat of evaporation of metals. This can be attributed to particles overcoming the barrier activation of self-diffusion, to a class of liquid- mobile particles within the concept of randomized particles.

This concept is based on the Boltzmann’s distribution [2] , which is relative to the kinetic energy of random thermal motion of the particles is not only true for the gas, but the condensed state of matter [3] . According to this concept [4] -[7] , the particles having an energy not higher than the melting heat are responsible for the long- range order of bonds, although a virtual character of their stay in the crystal lattice in the solid state or in the fragments of this lattice (clusters) in a liquid or gaseous states. These particles are called crystal-mobile and their share at any temperature according to the Boltzmann’s distribution expressed by the relation

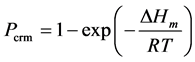. (1)

Particles with energies above the boiling heat are most randomized, fragmented, and they are named vapor- mobile. They are characterized by a zero bond order, and their share is subject to dependence

. (2)

Particles with energies the random motion higher than of the heat of melting, but lower than the heat of eva- poration, are responsible for the short-range order of unstructured communication, called liquid-mobile. Their share is the difference between one and the shares crystal-mobile and vapor-mobile

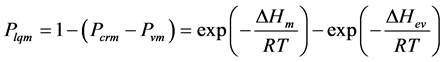. (3)

Since the sum of share crystal-, liquid- and vapor-mobile particles according to the Boltzmann’s distribution is strictly equal to unity, the particles always exist together at all temperatures (except 0 and), and, therefore, in any physical states-solid, liquid and gas, changing them only their ratio and constantly exchanging energy.

The fact that the particles are able to self-diffusion in the solid state and the energy corresponds to the range of the existence of liquid-mobile particles, indicates a further important physical sense of this class of rando- mized particles. In addition to providing plasticity and solubility of metals, which are discussed in [8] , liquid- mobile particles being also diffusing on this basis more specifically reveal its mobile nature and mechanism of the plasticity and solubility of the transition from the state of thermodynamic equilibrium to a nonequilibrium kinetic.

The regular relationship the activation energy of self-diffusion with heat melting and boiling point can be illu- strated by statistical analysis of the data in Table 1. Thus, the relationship 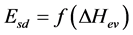may be found as straight- forward nature of the graphic placement of relevant data (Figure 1).

To express the linear nature of this relationship is first necessary to ensure the homogeneity of the set 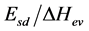(see Table 1). It can be installed by Nalimov’s criterion [9] [10]

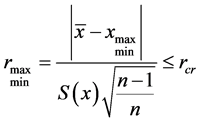(4)

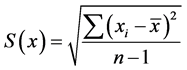, (5)

where―minimax value of the set,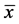―average value,―mean-square error,―volume of the set.

Normative values are tabulated Nalimov’s criterion 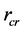for 5% level of significance are given in [10] , which are approximated in [8] , up to 5% to the equation

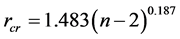. (6)

Here―the number of degrees of freedom Nalimov’s criterion.

For a given set of most deviant value 0.173 refers to plutonium, and then

.

Thus, the inequality is satisfied, the set of homogeneous, with a mean value is representative.

In this case, it is also important to justify the need to move the linear dependence of origin, as for physical reasons, it is obvious that for an arbitrarily small boiling heat of the self-diffusion activation energy is close to zero. The condition of the output line from the origin to the processing of any set is satisfied if the same or sub- stantially equal to two methods of averaging

. (7)

In this case,

.

Rounded up to the second significant digit obtain both embodiments the mean 0.52, helping equation relating the activation energy for self-diffusion in the form of heat of evaporation

(8)

Nonlinear coefficient of multiple correlation of calculated values with reference data was, with significance for its 95% confidence level [11] [12] . The coefficient of correlation for R. Shannon [13] determines the degree of determination of any model according to the expression. In this case, , indicating a key role in functional connection compared with the influence of random factors or un- accounted for determining the activation energy of self-diffusion as a function of heat of evaporation. It is possi- ble to also determine the confidence interval of this function, as recommended in [14]

, (9)

where and―maximum and minimum values in the experimental data set. For this case

,

that is ±20.6% of the average value of the function. This accuracy is typical for self-diffusion activation energy as the average for the different temperature ranges within the solid state of matter, very different for different metals.

Based on the understanding of the nature liquid-mobile particles that have the potential to leave the crystal lattice sites in excess of their thermal energy equal to, it appears that for self-diffusion, i.e. Brownian self- motion of the atoms in the crystal requires additional activation energy. Consequently, these particles must have an energy and be only part of the total share liquid-mobile particles. This proportion by analogy with the expression for the total share liquid-mobile particles (3) can be expressed as

. (10)

For illustration, we present a comparative calculations (3) and (10) for the melting point of the metal to have an idea of the total share liquid-mobile particles and that part which is provided by the self-diffusion, with the greatest development of the formation of these particles in the solid state (Table 2).

3. Discussion of Results

Here, first of all draws attention to the comparability of shares liquid-mobile particles for different metals with an average value of this indicator 0,382. Because contribute vapor-mobile the particles by melting temperature (and hence at lower) is negligibly small, not exceeding 10⁻⁹, the share of crystal-mobile particles to be the dif- ference value with a unit. As shown in [8] , the proximity of the relationship exactly at the point of destruction of the crystal melting to the proportion of the golden ratio (1.618) is not accidental and reveals the nature of this phase transition: above the melting point share of crystal-mobile particles responsible for long-range order due, and thus for the integrity of the crystal is smaller than this critical share and are not

capable of holding the crystal in the connected state. Apparently, the golden section relates to such a system- wide criteria that characterize an ideal limit for such a resistance ratio of the inner parts, when one of them pro- vides structural definition and the other―the optimum adaptability, flexibility [15] .

However, first need to check the homogeneity of the set. It is characterized by the greatest deviations again for plutonium, which has. Verification by Nalimov’s criteria gives the following results:

.

Consequently, the inequality is not satisfied, and “pop-up” value should be excluded from the set in question. It should be noted that while the demand for plutonium, it is an artificial radioactive element that is difficult to secure treatment [1] .

In plutonium excluded from the set of the average, and the most deviating value refers to cerium, accounting for 0.559. This gives a completely uniform set of:

,

and new average value within the mean-square error

includes the proportion of the golden section on unstructured component (0.382) with difference from the ad- justed average only 2.6%.

The proportion of self-diffusion particles, it is certainly much less than the total share of liquid-mobile par- ticles, which serve as a kind of reservoir for the more energetic particles. Because it is a deviation from the equi- librium solid state during the rapid heating, the elastic and plastic deformation and destruction of the crystal, on the one hand, and restoring the equilibrium state of the other. To initiate these processes is sufficient, only a small proportion of liquid-mobile particles closest to the heat of evaporation, accounting for about half of it. The very same proportion self-diffusion particles exceed the share vapor-mobile into two or more orders of magni- tude. This agrees very weak evaporation of solids in relation to their properties, to determine the existence of par- ticles liquid-mobile (solubility, plasticity), which, like other characteristics of the solid, liquid and gaseous states, reveals the same positions within the concept of randomized particles [16] [17] .

Given the diversity of bands change in the shares self-diffusion particles for various metals restrict example of the temperature dependence of for iron (Figure 2) according to (10).

4. Conclusions

1. On the example of typical metals it’s found that the activation energy for self-diffusion is above heat of melting and below heat of vaporization. This corresponds to the existence of liquid-mobile particle by classification based on the concept of randomized particles.

2. A formula for estimating the activation energy of self-diffusion by which it is approximately half of the heat of evaporation of the substance was suggested.

3. With the help of the temperature dependence for the share liquid-mobile particles expressed similar pattern to share self-diffusion particles. It is shown that the melting point of this share is typically less than 10⁻⁵.

4. Belonging of self-diffusion particles to the class liquid-mobile particles complement representation as the last tank of the equilibrium and non-equilibrium states of a crystalline substance such as a predisposition to dissolve or melt, to the elastic and plastic deformation, in which the role of self-diffusion particle most high energy status is reduced to initiate appropriate changes in these states.

References