Open Journal of Physical Chemistry
Vol.05 No.03(2015), Article ID:58339,15 pages
10.4236/ojpc.2015.53008
A Method for Calculating the Heats of Formation of Medium-Sized and Large-Sized Molecules
Bing He1,2, Hongwei Zhou1,3*, Fan Yang1, Wai-Kee Li4
1Molecular Design Institute, Chengdu Normal University, Chengdu, China
2State Key Laboratory of Biotherapy and Cancer Center, West China Hospital, Sichuan University, and Collaborative Innovation Center for Biotherapy, Chengdu, China
3IPNL, UMR IN2P3-CNRS-UCBL 5822, Villeurbanne, France
4Department of Chemistry, The Chinese University of Hong Kong, Hong Kong, China
Email: *jcbzhou@sina.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2015; accepted 25 July 2015; published 28 July 2015
ABSTRACT
A calculation method for heats of formation (HOF, referred to as DHf) based on the density functional theory (DFT) is presented in this work. Similar to Gaussian-3 theory, the atomic scheme is applied to calculate the heats of formation of the molecules. In this method, we have modified the formula for calculation of Gaussian-3 theory in several ways, including the correction for diffuse functions and the correction for higher polarization functions. These corrections are found to be significant. The average absolute deviation from experiment for the 164 calculated heats of formation is about 1.9 kcal・mol−1, while average absolute deviation from G3MP2 for the 149 (among the 164 molecules, 15 large-sized molecules can not be calculated at the G3MP2 level) calculated heats of formation is only about 1.9 kcal・mol−1. It indicates that the present method can be applied to predict the heats of formation of medium-sized and large-sized molecules, while the heats of formation of these molecules using Gaussian-3 theory are much difficult, even impossible, to calculate. That is, this method provides a choice in the calculation of DHf for medium-sized and large- sized molecules.
Keywords:
Heats of Formation, Gaussian-3 Theory, Energy, Absolute Deviation

1. Introduction
Quantum chemical methods for the calculation of thermochemical data have been developed beyond the level of just reproducing experimental data and can now make accurate predictions where the experimental data are unknown or uncertain. The more accurate one in these methods is the Gaussian-n theory [1] -[8] , which has been widely used to estimate the heats of formation [7] [8] of small-sized molecules. For example, in an assessment [9] of Gaussian-3 (G3) theory on the 148 calculated heats of formation of neutral molecules, the average absolute deviation from experiment is less than 1 kcal・mol−1. This means that G3 theory can be used to predict heats of formation of molecules accurately. However, there are some deficiencies in G3 theory and its variation (commonly referred to as G3MP2 theory and G3B3 theory), such as, i) they can only be used to calculate the heats of formation of small-sized molecules, but become computationally intensive with the increasing number of atoms in molecules, and ii) there are large deviations for some molecules, especially for polynitrogen compounds, which are the potential candidates of high energy density materials. Especially, Gaussian-4 (G4) theory [8] and various modifications that recently come out show good accuracy for the calculation of heats of formations, the aforementioned deficiencies still exist.
The correlation method for calculation of heats of formation has drawn tremendous interest to find better ways to match the computational requirements of medium-sized and large-sized molecules, including isodesmic reaction schemes [9] -[14] , group additive method, molecular mechanics and semiempirical methods [13] [15] - [17] , and linear regression correction approach [18] , etc. For the isodesmic reactions method, it is important to construct an appropriate bond separation reaction in which DHf for all components, except the target component, are known. A bond separation reaction is a reaction which breaks down any molecule composed of three or more heavy atoms, and which can be represented in classical valence structure, into its simplest set of two heavy atom molecules containing the same type of bond, i.e. the number and types of all bonds are retained. Sometimes this approach is very difficult. Of cause, it does not incorporate the energy stabilization effect caused by conjugate bonds in polyene or aromatic compounds. For group additive method, molecular mechanics, semiempirical methods [13] [15] -[17] and linear regression correction approach [18] , the results are strongly dependent on the parameters used and thus are less reliable because they are all parameterized methods. For example, the thermochemical parameters can be obtained easily by the semiempirical methods, but the heats of formation based on these parameters are either underestimated or overestimated. The deviations are so large that a set of terms are introduced to correct the heats of formation in agreement with experimental values. So, semiempirical methods cannot be used to predict heats of formation of compounds if the experimental data are unknown.
Ab initio MO method and density functional theory (DFT), on the other hand, are independent on the experimental results and parameters, and have emerged as a very reliable method to calculate geometries, energies, and frequencies of molecules. Hence, they have been used to evaluate the DHf of interested molecules [15] [16] [19] [20] . Dunning’s correlation consistent basis sets [21] -[23] (cc-pV*Z, where * denotes double, triple, quad- ruple, quintuple-zeta and sextuple-zeta, respectively) have the redundant functions removed and have been rotated [24] in order to increase computational efficiency. By combining the DFT with cc-pVDZ, the calculation results will be reliable. However, DFT/cc-pVDZ calculations do not produce DHf directly, so special model reactions have to be designed to derive the DHf (referred to as DFT DHf) from the calculated total energy and vibrational analysis results [25] -[27] . This is also the goal we will pursue.
Our objective is to develop a procedure applicable to any molecular system in an unambiguous manner, which can reproduce experimental data to an accuracy of about of 2 kcal・mol−1 even to species having larger experimental uncertainty. Recently, we have investigated the relative stabilities of N2n (N6 (D3h), N8 (Oh), N10 (D5h), N12 (D6h), N12 (D3d), N16 (D4d), N18 (D3h), N20 (Ih), N24 (D3d), N24 (D4h), N24 (D6d), N30 (D3h), N30 (D5h), N32 (D4d), N36 (D3d), N40 (D4h), N42 (D3h), N48 (D4d), N48 (D3d), N54 (D3h), N56 (D4h), N60 (D3d) and N72(D3d)) [28] [29] molecules at B3LYP/cc-pVDZ. As the potential candidates of high energy density materials, one important issue is to calculate the DHf of the molecules. However, the calculations of DHf of the molecules from N16 to N72 are very difficult, even impossible using Gaussian-n theory because these molecules are medium-sized or large-sized and the experimental energies have not been well established. Furthermore, we found that Gaussian-n theory performed poorly on the polynitrogen compounds (about 2 kcal・mol−1 for each nitrogen atom in the molecules). In such case, the computational method for heats of formation based on DFT (referred to as DFT method) was conceived as the first in a series of well defined methods that could be routinely applied to the calculation of molecular energies of these medium-sized and large-sized molecules in a systematic manner and indeed, the results agreed with experimental values and so were reliable.
2. Theoretical and Computational Method
For the reaction Reactants ® Product:
The heats of formation at 298 K (DHf) can be calculated by Equation (1).
 (1)
(1)
where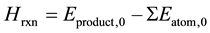 ;
;
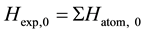 , which can be obtained from Ref. [30] ;
, which can be obtained from Ref. [30] ;
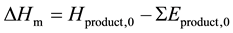 ;
;
DHatom = ΣHatom, which can be obtained from Ref. [30] .
Thereof, terms Hexp,0 and DHatom in Equation (1) are constants for the specified product whatever calculation methods are used to obtain the thermodynamic data. While terms Hrxn and DHm vary with different computational levels.
Equation (1) is applied to calculate the DHf of a compound in G3 theory and G3MP2 theory (referred to as G3MP2 DHf), where total energy of the product (Eproduct,0) and total energy of each atom of the reactants (ΣEatom,0) are referred to as “G3 (0 K)” or and “G3MP2 (0 K)”. G3 (0 K) or G3MP2 (0 K) are modified by a series of corrections (referred to as Ec) from additional calculations, including a correction for diffuse functions [9] [10]
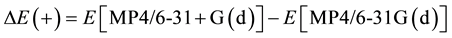 (2)
(2)
and a correction for higher polarization functions on nonhygrogen atoms and p-functions on hydrogens, [9] [10] etc.
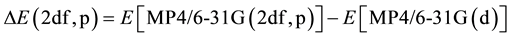 . (3)
. (3)
It can be found that the key issue is to obtain Eproduct,0 and Eatom,0. In our work, only the total energy at the level B3LYP/cc-pVDZ can be obtained. Similar to the G3 theory and G3MP2 theory, the total energy at the level B3LYP/cc-pVDZ is modified by a correction for diffuse functions
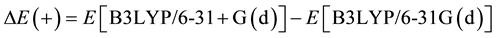 (4)
(4)
and a correction for higher polarization functions on nonhygrogen atoms and p-functions on hydrogens.
 . (5)
. (5)
Comparing to the 6
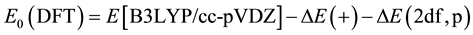 (6)
(6)
where E0 (DFT) is the energy of each atom of the reactants that Equation (1) requires. The correction energy is defined as Ec, which can be written as
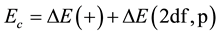 . (7)
. (7)
Note that for H (Hydrogen) to O (Oxygen) atoms, DE (+) will be removed from E0 (DFT), for fluorine atom, and DE (2df, p) will be removed from E0 (DFT). According to the above corrections, Ec for the first and second row atoms are listed in Table 1.
A number of deficiencies in the method should be noted and future developments to alleviate them are proposed. In particular, this method works poorly on dissociation energies of ionic molecules such as LiF, on inorganic molecules such as CO2 (5.6 kcal・mol−1 too low), NH3 (3.7 kcal・mol−1 too large). Also, it works poorly on the hypervalent species, such as -SO2 group and -NO2 group, where their energies are high by 19 - 21 kcal・mol−1 for the -SO2 group and low by 9 - 10 kcal・mol−1 for the -NO2 group. It was found that additional group corrections might reduce discrepancy so that experimental values could be fitted perfectly.
Now, the total energy and the enthalpy of the product can be obtained from quantum chemistry calculation
Table 1. The atomic energies of the first row and the second row.
E0: energy of each atom of the reactants (au); H0: the experimental heats of each atom of the reactants (kcal・mol−1); Hm: the correction value of the experimental heat of each atom of the reactants (kcal・mol−1); Ec: the correction energy (au).
directly. The DHexp,0 and DHatom can be obtained from correlative books [30] . The DHf of a molecule at the level B3LYP/cc-pVDZ can be calculated by Equation (1) via Equation (6).
3. Results and Discussion
In this work, 164 compounds are selected for testing. They are divided into four test sets: i) G2/97 test set, ii) CH test set, iii) NOS test set, and iv) LARGE test set.
3.1. G2/97 Test Set
There are 70 neutral molecules in this test set. The structures are taken from Ref. [9] . All calculations are carried out using the GAUSSIAN 98 program package [31] . Density Function Theory has been applied to optimize the structures at basis set cc-pVDZ. The basis sets are the correlation-consistent basis sets of Dunning, specifically the polarized valence double-ζ (cc-pVDZ). The convergence criterion is 10−8. The optimized structures of the 70 species at the level B3LYP/cc-pVDZ and G3MP2 are shown in Table 2. The harmonic vibrational frequencies have been predicted in these optimized structures. All the vibrational frequencies of the molecules both at the levels B3LYP/cc-pVDZ and G3MP2 are positive (not listed). This indicates that the molecules are at a local minimum at the levels B3LYP/cc-pVDZ and G3MP2.
In Table 2, the experimental DHf (Exp. column) are taken from Ref. [9] . Some values have been updated by values from Ref. [30] , such as the experimental value for 02 is changed from −118.4 kcal・mol−1 to −119.4 kcal・mol−1, for 48 from 8.9 kcal・mol−1 to 5.0 kcal・mol−1, etc.
It can be found that the DFT DHf deviations from experiment in some molecules are comparatively high (It is noted that the absolute DHf deviations which are greater than 2.5 kcal・mol−1 are in bold and italic in Table 2 and the subsequent tables): 01 (−7.1 kcal・mol−1), 12 (−2.5 kcal・mol−1), 13 (−3.1 kcal・mol−1), 31 (−6.0 kcal・mol−1), 37 (−2.5 kcal・mol−1), 41 (−2.6 kcal・mol−1), 50 (−2.7 kcal・mol−1), 51 (−3.1 kcal・mol−1), 53 (−4.9 kcal・mol−1), 56
Table 2. The DHf and the deviations from experiment of the 70 selected molecules of the G2/97 test set. All are in kcal・mol−1.
Exp.: experimental DHf taken form Ref. [30] ; G3MP2: DHf obtained at the level G3MP2; DFT: DHf obtained at the level B3LYP/cc-pVDZ; G3Dev: G3MP2 DHf deviation from experiment; DFTDev: DFT DHf deviation from experiment. Deviations which exceed 2.5 are in bold and italic.
(−2.7 kcal・mol−1), 58 (−3.3 kcal・mol−1) and 65 (−2.7 kcal・mol−1). The 01 (C
The G3MP2 DHf deviations of some molecules from experiment value are also comparatively high: 01 (−3.7 kcal・mol−1), 02 (−4.4 kcal・mol−1), 10 (2.8 kcal・mol−1), 13 (2.9 kcal・mol−1), 30 (5.1 kcal・mol−1), 32 (2.7 kcal・mol−1), 39 (4.7 kcal・mol−1) and 70 (3.1 kcal・mol−1). It can be found that G3MP2 does poorly on the halides, too. 01 and 02 belong to this category. G3MP2 also works poorly on the molecules which contain cumulated double-bond (-X=C=Y-), 01 (−0.9 kcal・mol−1) and 10 belong to this category. Both DFT and G3MP2 work poorly on the bicyclobutane (
The G3MP2 DHf deviations and the DFT DHf deviations from experiment value are shown in Figure 1. It can be found that the trends of the two lines are identical for the same molecule if the deviation is neglected. Most of the G3MP2 DHf deviations from experiment are positive, while most of the DFT DHf deviations from experiment are negative.
It is noted that the molecule structures are taken from the original test set of G3 theory [9] (G2/97 test set), where a “higher level correction” (HLC) [9] is added to take into account some deficiencies in the energy calculations.
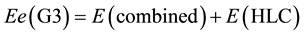
The HLC is −Anβ − B(nα − nβ) for molecules and −Cnβ − D(nα − nβ) for atoms (including atomic ions). The nβ and nα are the number of β and α valence electrons, respectively, with nα ≥ nβ. The number of valence electron pairs corresponds to nβ. Thus, A is the correction for pairs of valence electrons in molecules, B is the correction for unpaired electrons in molecules, C is the correction for pairs of valence electrons in atoms, and D is the correction for unpaired electrons in atoms. The use of different corrections for atoms and molecules can be justified,
Figure 1. DFT DHf and G3MP2 DHf deviations from experiment of the G2/97 test set.
in part, by noting that these extrapolations take some account of effects of basis functions with higher angular momentum, which are likely to be of more importance in molecules than in atoms. For G3 theory, A = 6.386 mhartrees, B = 2.977 mhartrees, C = 6.219 mhartrees, D = 1.185 mhartrees. The A, B, C, D values are chosen to give the smallest average absolute deviation from experiment for the G2/97 test set. Obviously, A, B, C and D are the fit parameters which are taken into account the electron structures of molecules in G2/97 test set, and in turn, they are used to calculate the energies of molecules in the same test set. That is, the precisions for calculation energies, especially for the molecules in the test set, are improved by introducing the fit parameters A, B, C, D. In this circumstances, it is not strange that the average absolute deviation of G3MP2 DHf from experiment is less than that of DFT DHf.
3.2. CH Test Set
There are 20 neutral molecules which are all typical hydrocarbons in this test set. All calculations are carried out using the GAUSSIAN 98 program package. Density Function Theory (DFT) has been applied to optimize the structures at basis set cc-pVDZ. The optimized structures of the 20 species at the levels B3LYP/cc-pVDZ and G3MP2 are shown in Table 3. The harmonic vibrational frequencies have been predicted in these optimized structures. All the vibrational frequencies of the molecules both at the levels B3LYP/cc-pVDZ and G3MP2 are positive (not listed). This indicates that the molecules are at local minimum at the levels B3LYP/cc-pVDZ and G3MP2.
In Table 3, the experimental DHf (Exp. column) are taken from Ref [30] . It can be found that the DFT DHf deviations of some molecules from experiment value are comparatively large: 01 (3.7 kcal・mol−1), 15 (−4.5 kcal・mol−1) and 18 (4.0 kcal・mol−1). For 01 and 18, both contain a functional group -C≡C-. It indicates that this method works poorly on the species. As is known, the isodesmic method for calculation does not incorporate the energy stabilization effect caused by conjugated bonds in polyene or aromatic compounds. It can also be found that the present method works poorly on polyene or aromatic species. The molecules 02, 03, 05, 15, 18 belong to conjugated category. The sum of absolute deviation from experiment for the 20 calculated heats of formation is 36.3 kcal・mol−1. The average absolute deviation from experiment is about 1.8 kcal・mol−1.
In this test set, the G3MP2 DHf deviations of some molecules from experiment are also comparatively high: 02 (−4.2 kcal・mol−1), 04 (−3.3 kcal・mol−1), 13 (−3.3 kcal・mol−1), 15 (−5.7 kcal・mol−1), 16 (3.0 kcal・mol−1), 19 (−5.6 kcal・mol−1) and 20 (−3.8 kcal・mol−1). These results show that G3MP2 theory, which is known as the isodesmic method, for calculation does not incorporate the energy stabilization effect caused by conjugated bonds in polyene or aromatic compounds. Whereas 02, 04, 013, 15, 16, 19, 20 belong to conjugated category. It can be found that the number of G3MP2 DHf deviations is more than that of the DFT DHf deviations. And comparing the G3MP2 DHf deviations and the DFT DHf deviations, one can find that the former is higher than that of the later. The sum of absolute deviation from experiment for the 20 calculated heats of formation is 45.4 kcal・mol−1. The average absolute deviation is about 2.3 kcal・mol−1.
The G3MP2 DHf deviations and the DFT DHf deviations from experiment are shown in Figure 2. It can be found that the trends of the two lines are identical for the same molecule if the deviation sign is neglected. Most of the G3MP2 DHf deviations from experiment are negative, while most of the DFT DHf deviations from experiment are possibly negative or positive. From the view of point of average absolute deviation from experiment, DFT DHf method is more preferable than the G3MP2 DHf method in this test set.
3.3. NOS Test Set
There are 60 neutral molecules in this test set. All calculations are carried out using the GAUSSIAN 98 program package. Density Function Theory (DFT) has been applied to optimize the structures at basis set cc-pVDZ. The optimized structures of the 60 species at the levels B3LYP/cc-pVDZ and G3MP2 are shown in Table 4. The harmonic vibrational frequencies have been predicted in these optimized structures. All the vibrational frequencies of the molecules both at the level B3LYP/cc-pVDZ and G3MP2 are positive (not listed). This indicates that the molecules are at local minimum at B3LYP/cc-pVDZ and G3MP2.
In Table 4, the experimental DHf (Exp. column) are taken from Ref [30] . In this test set, we selected some typical molecules which contain special functional groups, such as -NO2, -SO2, -X=C=Y-, etc. The calculation results show that each -NO2 group may be low by 9.6 kcal・mol−1, and each -SO2 group may be high by 20.0 kcal・mol−1. In order to fit for the experimental values, 9.6 kcal・mol−1 is added for the DFT DHf for each -NO2
Table 3. The DHf and the deviations from experiment of the 20 molecules of the CH test set. All are in kcal・mol−1.
Exp.: experimental DHf taken form Ref. [30] ; G3MP2: DHf obtained at the level G3MP2; DFT: DHf obtained at the level B3LYP/cc-pVDZ; G3Dev: G3MP2 DHf deviation from experiment; DFTDev: DFT DHf deviation from experiment.
group a molecule contains, and 20.0 kcal・mol−1 is subtracted from the DFT DHf for each -SO2 group a molecule contains. The listed DFT DHf values in Table 4 are corrected by the two values, 9.6 kcal・mol−1 and 20.0 kcal・mol−1.
In Table 4, it can be found that the DFT DHf deviations of some molecules from experiment are comparatively large: 03 (3.7 kcal・mol−1), 07 (−4.0 kcal・mol−1), 08 (−6.3 kcal・mol−1), 11 (−5.7 kcal・mol−1), 12 (−3.1 kcal・mol−1), 18 (−3.2 kcal・mol−1), 23 (3.3 kcal・mol−1), 25 (−4.0 kcal・mol−1), 27 (−4.1 kcal・mol−1), 28 (−3.2 kcal・mol−1), 29 (−4.6 kcal・mol−1), 33 (3.5 kcal・mol−1), 34 (−2.7 kcal・mol−1), 41 (−2.7 kcal・mol−1), 42 (−2.7 kcal・mol−1), 48 (−3.4 kcal・mol−1), 50 (3.4 kcal・mol−1), 51 (−6.0 kcal・mol−1), 53 (−5.0 kcal・mol−1), 54 (−4.9
Table 4. The DHf and the deviations from experiment of the 60 molecules of the NOS test set. All are in kcal・mol−1.
Exp.: experimental DHf taken form Ref. [30] ; G3MP2: DHf obtained at the level G3MP2; DFT: DHf obtained at the level B3LYP/cc-pVDZ; G3Dev: G3MP2 DHf deviation from experiment; DFTDev: DFT DHf deviation from experiment.
Figure 2. DFT DHf and G3MP2 DHf deviations from experiment of the CH test set.
kcal・mol−1) and 55 (−4.3 kcal・mol−1). Among these molecules, 03, 23, 48, 51, 53, 54, 55 contain the -NO2 group, 27 and 28 contain the -SO2 group, and 07, 18, 41, 42 contain the -CO2 group, while 08, 11, 12, 33, 34 contain the -X=C=Y- group. As mentioned above, the DFT DHf method works poorly on these species. The sum of absolute deviation from experiment for the 60 calculated heats of formation is 132.3 kcal・mol−1. The average absolute deviation is about 2.2 kcal・mol−1.
In this test set, the G3MP2 DHf deviations of some molecules from experiment value are also comparative high: For the molecules contain the -NO2 group, 02 (2.6 kcal・mol−1), 03 (2.7 kcal・mol−1) and 22 (3.5 kcal・mol−1); for the molecules contain the -SO2 group, 17 (3.7 kcal・mol−1), 27 (4.5 kcal・mol−1), 28 (9.2 kcal・mol−1) and 32 (4.2 kcal・mol−1); for the molecules contain the -X=C=Y- group, 07 (6.2 kcal・mol−1), 08 (6.3 kcal・mol−1), 10 (6.3 kcal・mol−1), 12 (−5.2 kcal・mol−1), 33 (10.2 kcal・mol−1) and 35 (−4.7 kcal・mol−1); For the molecules contain the -CO2 group, 07 (6.2 kcal・mol−1), 15 (4.6 kcal・mol−1) and 42 (3.7 kcal・mol−1). Furthermore, the G3MP2 DHf deviations of polynitrogen compounds, 06 (6.5 kcal・mol−1), 09 (5.1 kcal・mol−1), 10 (6.3 kcal・mol−1), 13 (6.7 kcal・mol−1), 14 (3.2 kcal・mol−1), 15 (4.6 kcal・mol−1) and 32 (4.2 kcal・mol−1), and of boron compounds, 29 (4.5 kcal・mol−1) and 47 (4.9 kcal・mol−1), are high. These results show that G3MP2 theory works poorly on these species. The sum of absolute deviation from experiment for the 59 calculated heats of formation, wherein the molecule 48 cannot be calculated at G3MP2, is 157.0 kcal・mol−1. The average absolute deviation from experiment for the 59 calculated G3MP2 DHf is 2.7 kcal・mol−1.
The G3MP2 DHf deviations and the DFT DHf deviations from experiment value are shown in Figure 3. It can be found that most of the G3MP2 DHf deviations from experiment value are positive, while most of the DFT DHf deviations from experiment value are possibly negative or positive. From the judgment of average absolute deviation from experiment value, the DFT DHf method is more preferable than that of G3MP2 DHf method in the test set because the average absolute deviation from experiment of the DFT DHf is lower than that of the G3MP2 DHf.
The sum of the absolute deviations from experiment is 278.7 for the above 150 calculated DFT DHf. While the sum of the absolute deviations from experiment is 281.0 for the above 149 calculated G3MP2 DHf. Both of the average absolute deviations are about 1.9 kcal・mol−1 (1.89 kcal・mol−1 for G3MP2 theory, 1.86 kcal・mol−1 for DFT method). The average absolute deviation of G3MP2 theory for the 70 molecules in G2/97 test set is only 1.1 kcal・mol−1, while the average absolute deviations of the remaining two test sets are very high (2.3 kcal・mol−1 for CH test set, and 2.7 kcal・mol−1 for NOS test set) because the former is the original test set while the later are not. Whereas, the average absolute deviations of DFT method the results are from 1.6 kcal・mol−1 to 2.2 kcal・mol−1 for all the three test sets. By taking this into account, we can conclude that the DFT method is the same effective as the G3MP2 theory in predication of DHf of compounds.
3.4. LARGE Test Set
There are 14 neutral molecules in this test set. All calculations are carried out using the GAUSSIAN 98 program package. DFT has been applied to optimize the structures at basis set cc-pVDZ. The optimized structures of the
Figure 3. DFT DHf and G3MP2 DHf deviations from experiment of the NOS test set.
Table 5. The DHf and the deviations from experiment of the 14 molecules of the LARGE test set. All are in kcal・mol−1.
Exp.: experimental DHf taken form Ref. [30] ; DFT: DHf obtained at the level B3LYP/cc-pVDZ; DFTDev: DFT DHf deviation from experiment.
14 species at the level B3LYP/cc-pVDZ are shown in Table 5. The harmonic vibrational frequencies have been predicted in these optimized structures. All the vibrational frequencies of the molecules at the level B3LYP/cc- pVDZ are positive (not listed). This indicates that the molecules are at local minimum at the level B3LYP/cc- pVDZ.
In Table 5, the experimental DHf (Exp. column) are taken from Ref. [30] . In this test set, we selected some medium-sized and large-sized molecules, of which the calculation of heats of formation of these molecules using G3 or G3MP2 theory is much difficult, even impossible.
From Table 5, it can be found that the DFT DHf deviations of some molecules from experiment value are comparative large: 02 (−4.9 kcal・mol−1), 04 (−3.1 kcal・mol−1), 05 (−5.8 kcal・mol−1), 06 (−5.6 kcal・mol−1), 07 (3.4 kcal・mol−1), 08 (2.7 kcal・mol−1) and 12 (3.3 kcal・mol−1). Among them, the deviations of the molecules 04 and 05 are mainly caused by the halogen atoms in the molecules. While the deviations of the molecules 02 and 06 are mainly caused by the -CO2 group. The sum of absolute deviation from experiment for the 14 calculated heats of formation is 36.5 kcal・mol−1. The average absolute deviation from experiment for the 14 calculated heats of formation is about 2.6 kcal・mol−1. It seems that the average absolute deviation is comparatively high in this test set. However, the high absolute deviation 5.8 kcal・mol−1, for example in 05, is acceptable because the molecules are the medium-sized and large-sized.
4. Conclusion
In this work, we have developed a method for calculating the heats of formation of medium-sized and large- sized molecules. This method has the following characteristics: i) The calculation formula for the heats of formation is derived from the famous G3 and G3MP2 theory. The atomic energies are obtained from the calculated results. There are no empirical parameters or fit parameters to be introduced to eliminate the deficiencies in the calculation of the heats of formation except the corrections of the chemical functional groups -NO2 and -SO2. ii) The average absolute deviation from experiment for the 150 calculated DFT DHf is 1.5 kcal・mol−1. While the average absolute deviation from experiment for the 149 calculated G3MP2 DHf is 1.7 kcal・mol−1. The average absolute deviation from experiment for the whole 164 calculated DFT DHf is also 1.9 kcal・mol−1. The G3MP2 DHf and DFT DHf can be used to predict the heats of formation when the experimental data are unknown or uncertain. iii) The present method can be applied to predict the heats of formation of medium-sized and large-sized molecules. The heats of formation of a molecule containing 100 up to 200 heavy atoms can be calculated by this method. Under economical consideration, this method is expected to impact the applications in the calculations of heats of formation of large-sized molecules.
Cite this paper
BingHe,HongweiZhou,FanYang,Wai-KeeLi, (2015) A Method for Calculating the Heats of Formation of Medium-Sized and Large-Sized Molecules. Open Journal of Physical Chemistry,05,71-86. doi: 10.4236/ojpc.2015.53008
References
- 1. Curtiss, L.A., Raghavachari, K., Trucks, G.W. and Pople, J.A. (1991) Gaussian-2 Theory for Molecular Energies of First- and Second-Row Compounds. Journal of Chemical Physics, 94, 7221-7230.
http://dx.doi.org/10.1063/1.460205 - 2. Curtiss, L.A. and Raghavachari, K. (1995) In: Langhoff, S.R., Ed., Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, Kluwer Academic, Netherlands, 139.
- 3. Pople, J.A., Head-Gordon, M., Fox, D.J., Raghavachari, K. and Curtiss, L.A. (1989) Gaussian-1 Theory: A General Procedure for Prediction of Molecular Energies. Journal of Chemical Physics, 90, 5622-5629.
http://dx.doi.org/10.1063/1.456415 - 4. Curtiss, L.A., Jones, C., Trucks, G.W., Raghavachari, K. and Pople, J.A. (1990) Gaussian-1 Theory of Molecular Energies for Second-Row Compounds. Journal of Chemical Physics, 93, 2537-2545.
http://dx.doi.org/10.1063/1.458892 - 5. Curtiss, L.A., Raghavachari, K., Redfern, P.C. and Pople, J.A. (1997) Assessment of Gaussian-2 and Density Functional Theories for the Computation of Enthalpies of Formation. Journal of Chemical Physics, 105, 1063-1079.
http://dx.doi.org/10.1063/1.473182 - 6. Curtiss, L.A., Redfern, P.C., Raghavachari, K. and Pople, J.A. (1998) Assessment of Gaussian-2 and Density Functional Theories for the Computation of Ionization Potentials and Electron Affinities. Journal of Chemical Physics, 109, 42-55.
http://dx.doi.org/10.1063/1.476538 - 7. Lau, C.-K., Li, W.-K., Wang, X., Tian, A.M. and Wong, N.B. (2002) A Gaussian-3 Study of and Isomers. Journal of Molecular Structure (THEOCHEM), 617, 121-131.
http://dx.doi.org/10.1016/S0166-1280(02)00411-6 - 8. Curtiss, L.A., Redfern, P.C. and Raghavachari, K. (2011) Gn Theory. Wireless Communications & Mobile Computing, 1, 810-825.
- 9. Curtiss, L.A., Raghavachari, K., Redfern, P.C., Rassolov, V. and Pople, J.A. (1998) Gaussian-3 (G3) Theory for Molecules Containing First and Second-Row Atoms. Journal of Physical Chemistry, 109, 7764-7775.
http://dx.doi.org/10.1063/1.477422 - 10. Curtiss, L.A., Redfern, P.C., Raghavachari, K., Rassolov, V. and Pople, J.A. (1999) Gaussian-3 Theory Using Reduced Moller-Plesset Order. Journal of Chemical Physics, 110, 4703-4709.
http://dx.doi.org/10.1063/1.478385 - 11. Haworth, N.L. and Bacskay, G.B. (2002) Heats of Formation of Phosphorus Compounds Determined by Current Methods of Computational Quantum chemistry. The Journal of Chemical Physics, 117, 11175-11187.
http://dx.doi.org/10.1063/1.1521760 - 12. Gong, X.D., Zhang, J. and Xiao, H.M. (1999) Studies on the Synthesis of (2S,3R)-3-Hydroxy-3-Methylproline via C-2-N Bond Formation. Proceedings of the 26th International Pyrotechnics Seminar, 136.
- 13. Chen, Z.X., Xiao, J.M., Xiao, H.M. and Chiu, Y.N. (1999) Studies on Heats of Formation for Tetrazole Derivatives with Density Functional Theory B3LYP Method. The Journal of Chemical Physics, 103, 8062-8066.
http://dx.doi.org/10.1021/jp9903209 - 14. Hehre, W.J. (1995) Practical Strategies for Electronic Structure Calculation. Wavefunction, Inc., Irvine, 102-134.
- 15. Xu, X.J., Xiao, H.M., Ma, X.F. and Ju, X.H. (2006) Looking for High-Energy Density Compounds among Hexaazaadamantane Derivatives with Bond CN, Bond NC, and Bond ONO2 Groups. International Journal of Quantum Chemistry, 106, 1561-1568.
http://dx.doi.org/10.1002/qua.20909 - 16. Wang, G.X., Gong, X.D. and Xiao, H.M. (2009) Theoretical Investigation on Density, Detonation Properties, and Pyrolysis Mechanism of Nitro Derivatives of Benzene and Aminobenzenes. International Journal of Quantum Chemistry, 109, 1522-1530.
http://dx.doi.org/10.1002/qua.21967 - 17. Ruzsinszky, A., van Alsenoy, C. and Csonka, G.I. (2002) Optimal Selection of Partial Charge Calculation Method for Rapid Estimation of Enthalpies of Formation from Hartree-Fock Total Energy. The Journal of Physical Chemistry, 106, 12139-12150.
http://dx.doi.org/10.1021/jp026913s - 18. Duan, X.M., Song, G.L., Li, Z.H., Wang, X.J., Chen, G.H. and Fan, K.N. (2004) Accurate Prediction of Heat of Formation by Combining Hartree-Fock/Density Functional Theory Calculation with Linear Regression Correction Approach. The Journal of Chemical Physics, 121, 7086-7095.
http://dx.doi.org/10.1063/1.1786582 - 19. Jursic, B.S. (2003) Density Functional Calculation of the Heats of Formation for Various Aromatic Nitro Compounds. Journal of Molecular Structure (THEOCHEM), 634, 215-224.
http://dx.doi.org/10.1016/S0166-1280(03)00345-2 - 20. Chen, P.C., Chieh, Y.C. and Tzeng, S.C. (2000) Computing Heats of Formation for Cubane and Tetrahrane with Density Functional Theory and Complete Basis Set ab Initio Methods. Journal of Molecular Structure (THEOCHEM), 499, 137-140.
http://dx.doi.org/10.1016/S0166-1280(99)00293-6 - 21. Dunning, T.H. (1989) Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. The Journal of Chemical Physics, 90, 1007-1023.
http://dx.doi.org/10.1063/1.456153 - 22. Peterson, K.A., Woon, D.E. and Dunning Jr., T.H. (1994) Benchmark Calculations with Correlated Molecular Wave Functions. IV. The Classical Barrier Height of the H + H2 → H2 + H Reaction. The Journal of Chemical Physics, 100, 7410-7415.
http://dx.doi.org/10.1063/1.466884 - 23. Wilson, A., van Mourik, T. and Dunning Jr., T.H. (1997) Gaussian Basis Sets for Use in Correlated Molecular Calculations. VI Sextuple Zeta Correlation Consistent Basis Sets for Boron through Neon. Journal of Molecular Structure (THEOCHEM), 388, 339-349.
http://dx.doi.org/10.1016/S0166-1280(96)80048-0 - 24. Davidson, E.R. (1996) Comment on “Comment on Dunning’s Correlation-Consistent Basis Sets”. Chemical Physics Letters, 220, 514-518.
http://dx.doi.org/10.1016/0009-2614(96)00917-7 - 25. Berry, R.J., Burgess Jr., D.R.F., Nyden, M.R., Zacharian, M.R., Melius, C.F. and Schwarz, M. (1996) Halon Thermochemistry: Calculated Enthalpies of Formation of Chlorofluoromethanes. The Journal of Physical Chemistry, 100, 7405-7410.
- 26. Raghavachari, K., Stefanov, B.B. and Curtiss, L.A. (1997) Accurate Thermochemistry for Larger Molecules: Gaussian-2 Theory with Bond Separation Energies. The Journal of Chemical Physics, 106, 6764-6767.
http://dx.doi.org/10.1063/1.473659 - 27. Baboul, A.G., Curtiss, L.A., Redfern, P.C. and Raghavachari, K. (1999) Gaussian-3 Theory Using Density Functional Geometries and Zero-Point Energies. The Journal of Chemical Physics, 110, 7650-7657.
http://dx.doi.org/10.1063/1.478676 - 28. Zhou, H.W., Wong, N.B., Zhou, G. and Tian, A.M. (2006) Theoretical Study on “Multilayer” Nitrogen Cages. The Journal of Physical Chemistry A, 110, 3845-3852.
http://dx.doi.org/10.1021/jp056435w - 29. Zhou, H.W., Wong, N.B., Zhou, G. and Tian, A.M. (2006) What Makes the Cylinder-Shaped N72 Cage Stable? The Journal of Physical Chemistry A, 110, 7441-7446.
http://dx.doi.org/10.1021/jp062214u - 30. Lias, S.G., Bartmess, J.E., Liebman, J.F., Holmes, J.L., Levin, R.D. and Mallard, W.G. (1988) Gas-Phase Ion and Neutral Thermochemistry. Journal of Physical and Chemical Reference Data, 17.
- 31. Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G.A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H.P., Izmaylov, A.F., Bloino, J., Zheng, G., Sonnenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery Jr., J.A., Peralta, J.E., Ogliaro, F., Bearpark, M., Heyd, J.J., Brothers, E., Kudin, K.N., Staroverov, V.N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A., Burant, J.C., Iyengar, S.S., Tomasi, J., Cossi, M., Rega, N., Millam, J.M., Klene, M., Knox, J.E., Cross, J.B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi, R., Pomelli, C., Ochterski, J.W., Martin, R.L., Morokuma, K., Zakrzewski, V.G., Voth, G.A., Salvador, P., Dannenberg, J.J., Dapprich, S., Daniels, A.D., Farkas, Ö., Foresman, J.B., Ortiz, J.V., Cioslowski, J. and Fox, D.J. (2009) Gaussian 09. Revision C.01. Gaussian, Inc., Wallingford.
NOTES
*Corresponding author.






