Open Journal of Microphysics
Vol.3 No.3(2013), Article ID:35744,7 pages DOI:10.4236/ojm.2013.33012
The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling of the Planck Scale
Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2013 Mohamed S. El Naschie. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 1, 2013; revised July 1, 2013; accepted July 10, 2013
Keywords: Scaling the Planck Scale; Weyl Scaling; Nottale Scaling; Dark Energy; Quantum Relativity
ABSTRACT
The paper presents an exact analysis leading to an accurate theoretical prediction of the amount of the mysteriously missing hypothetical dark energy density in the cosmos. The value found, namely 95.4915028% is in full agreement with earlier analysis, the WMAP and the supernova cosmic measurements. The work follows first the strategy of finding a critical point which separates a semi-classical regime from a fully relativistic domain given by topological unit interval velocity parameter then proceeds to wider aspects of a topological quantum field of fractal unit interval. This idea of a critical velocity parameter was first advanced by Sigalotti and Mejias in 2006 who proposed a critical value equal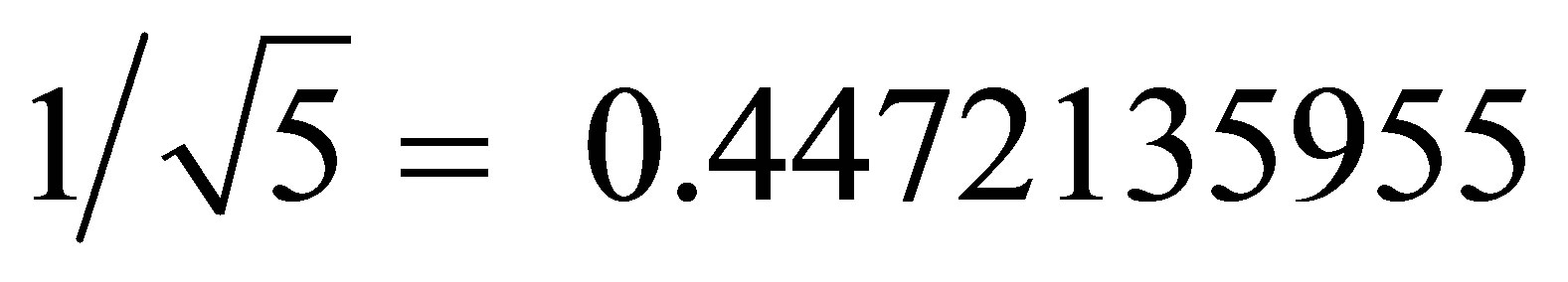 . A second interesting proposal made in 2012 by Hendi and Sharifzadeh set the critical point at 0.8256645. The present analysis is based upon a light cone velocity quantized coordinate. This leads to the same quantum relativity energy mass relation found in earlier publications by rescaling that of Einstein’s special relativity. Two effective quantum gravity formulae are obtained. The first is for the ordinary measurable energy of the quantum particle
. A second interesting proposal made in 2012 by Hendi and Sharifzadeh set the critical point at 0.8256645. The present analysis is based upon a light cone velocity quantized coordinate. This leads to the same quantum relativity energy mass relation found in earlier publications by rescaling that of Einstein’s special relativity. Two effective quantum gravity formulae are obtained. The first is for the ordinary measurable energy of the quantum particle 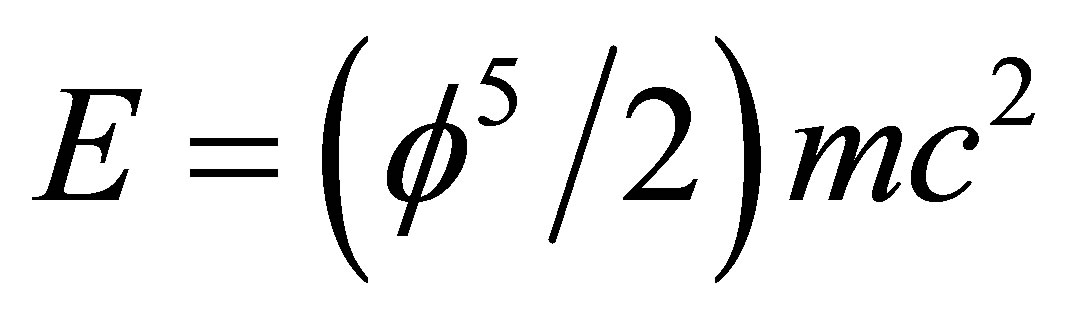 while the second is for dark energy density of the quantum wave which we cannot measure directly and we can only infer its existence from the measured accelerated expansion of the universe E(D) =
while the second is for dark energy density of the quantum wave which we cannot measure directly and we can only infer its existence from the measured accelerated expansion of the universe E(D) =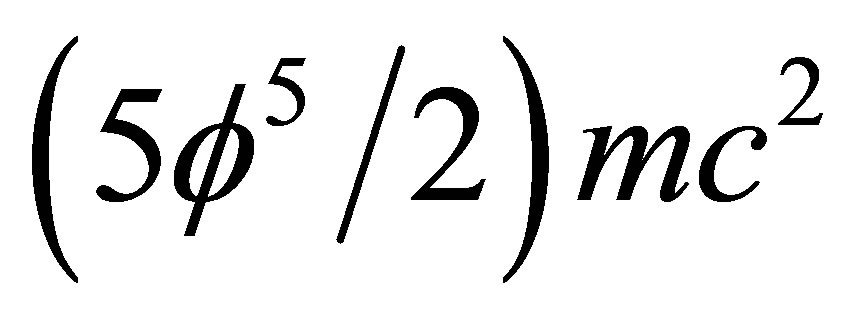 where
where . The critical velocity parameter in this case arises naturally to be
. The critical velocity parameter in this case arises naturally to be . The results so obtained are validated using a heuristic Lorentzian transformation. Finally the entire methodology is put into the wider perspective of a fundamental scaling theory for the Planck scale proposed by G. Gross.
. The results so obtained are validated using a heuristic Lorentzian transformation. Finally the entire methodology is put into the wider perspective of a fundamental scaling theory for the Planck scale proposed by G. Gross.
1. Introduction
The main objective of the present paper is to tackle head on the fundamental problem which conventional treatments of (i.e. special theory of relativity) poses for developing a theory for quantum gravity and understanding dark matter and dark energy [1-33]. We start with Sigalotti and Mejias’ discovery that the geometry of special relativity could be related to the geometry of a golden rectangular and deduced golden mean related value as a critical velocity parameter separating semi-classical and relativistic dynamics [1]. In a recent paper by Hendi and Sharifzadeh [2], the authors discussed Sigalotti et al’s discovery and added new conclusions and a critical velocity parameter. The present work follows at the beginning the basic strategy outlined in [1,2] in a slightly modified form and applies it to the major challenge of the missing hypothetical dark energy in the cosmos [3,4]. Using light cone coordinates, we define a light cone velocity and derive an effective quantum gravity formula for the energy-mass relation. The formula utilizes a critical light cone topological velocity parameter of the unit interval and predicts that dark energy density is 95.4915028% of the total energy density of the cosmos in full agreement with the cosmological measurements of WMAP and a certain major supernova [3] as well as previous analysis using different methods which will be discussed later on [24]. Incidentally the 2011 Nobel Prize in Physics went to the dedicated efforts to fulfill the daunting task of analyzing cosmic data from WMAP and supernova [3,4,15-17]. This incredible measurement achievement vitalized not only the science of quantum cosmology but in fact all of theoretical and high energy physics and may lend substantial justified importance to the present analysis [4,21,24]. Based on the present and previously obtained results we draw far reaching conclusions regarding a proposal by D. Gross to scale the Planck scale [26] as well as dark energy and its intimate relation with the particle-wave duality and quantum spacetime [15-18]. Finally in Sections 6 and 7, we briefly outline what could be termed a topological unit interval Cantorian field theory substantiating Biedenharn, Hurwitz and Gross visions [26-32].
2. Light Cone Coordinates and Critical Velocity
Similar to the light cone quantization of string theory we introduce light cone coordinates and velocity following the standard procedure [5]. Let the boost along the X direction be given by the velocity parameter [5]
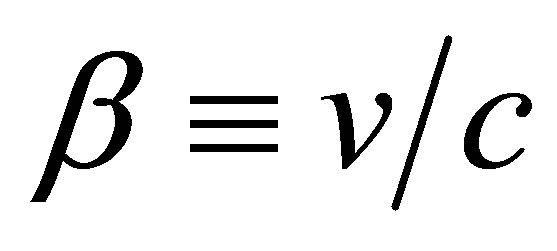 (1)
(1)
where v is the speed and c is the velocity of light. The Lorentz factor is then found from the Lorentz transformation as [5]
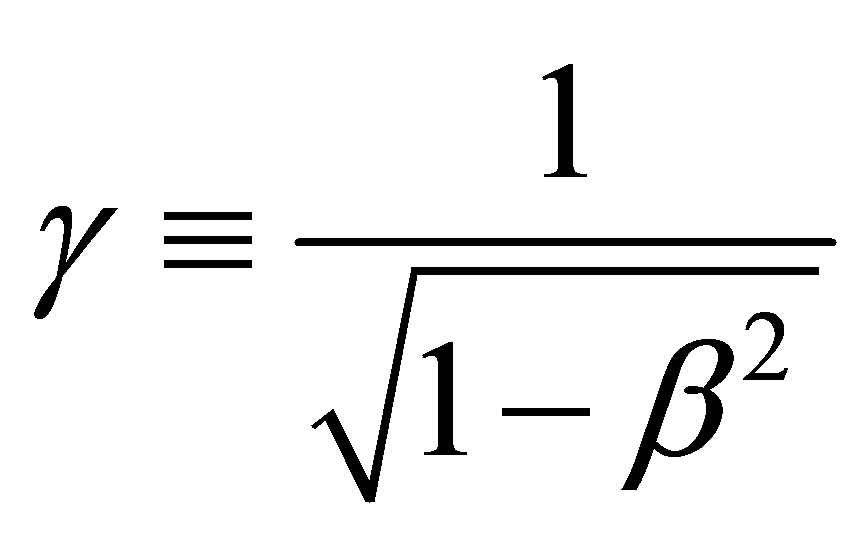 (2)
(2)
Now we introduce in the usual way the light cone coordinate [5]
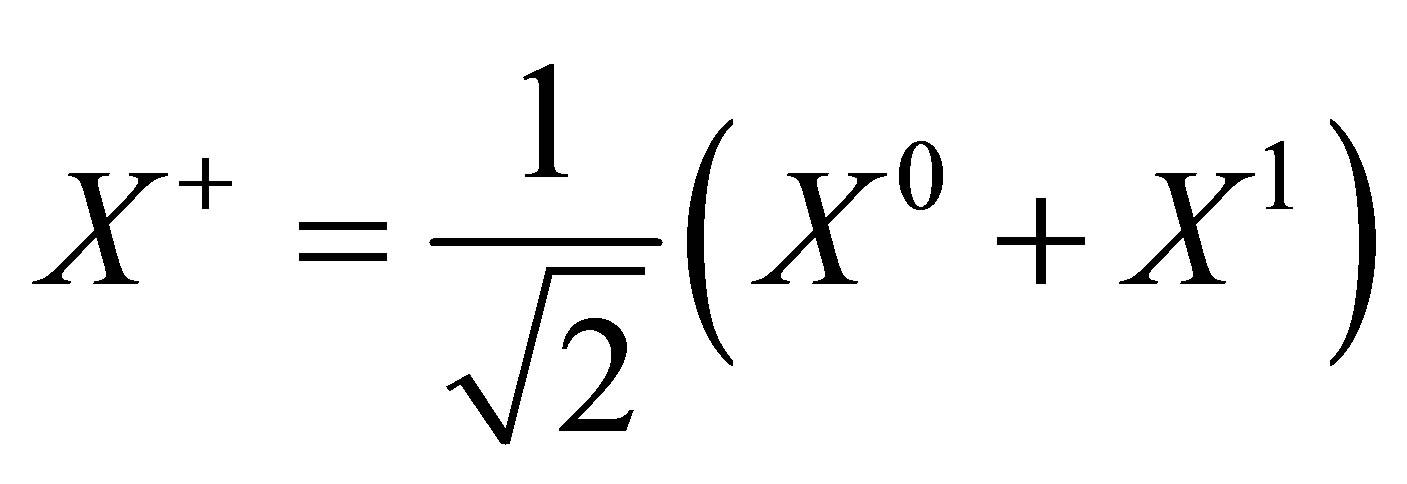 (3)
(3)
and
 . (4)
. (4)
Calling X+ time we are justified in looking at the rate of change of X− by X+ as light cone velocity
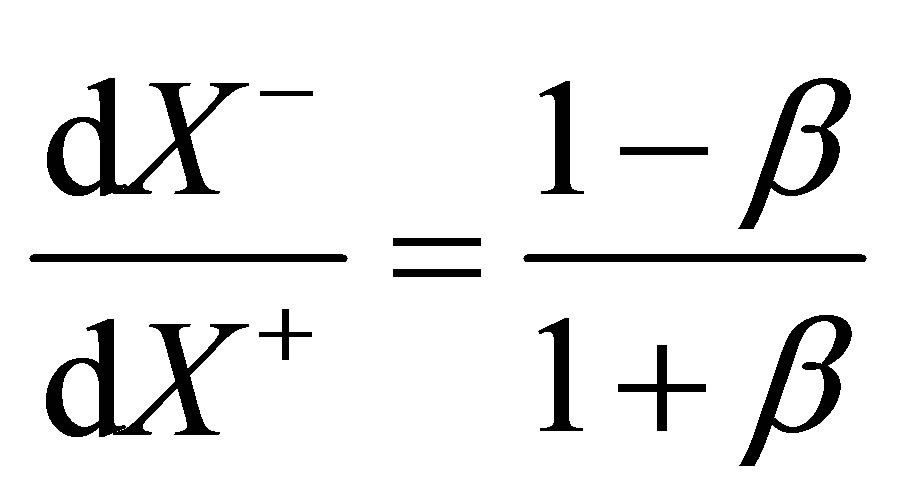 . (5)
. (5)
In the next section we will show how this point of view will impact the Lorentz factor and the classical energymass relationship  of special relativity [5-8].
of special relativity [5-8].
3. The Light Cone Critical Velocity Parameter and the Corresponding Energy-Mass Equation
As is well know, the relativistic energy is given by Einstein’s famous equation
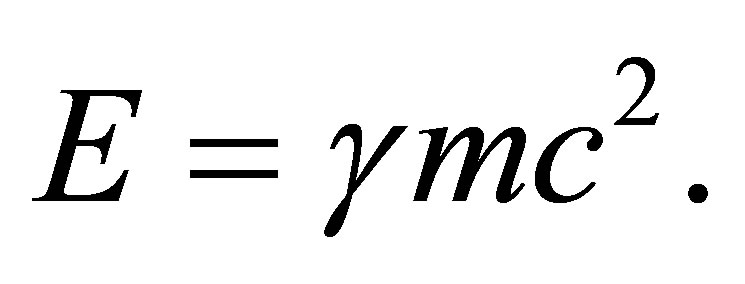 (6)
(6)
First we note that
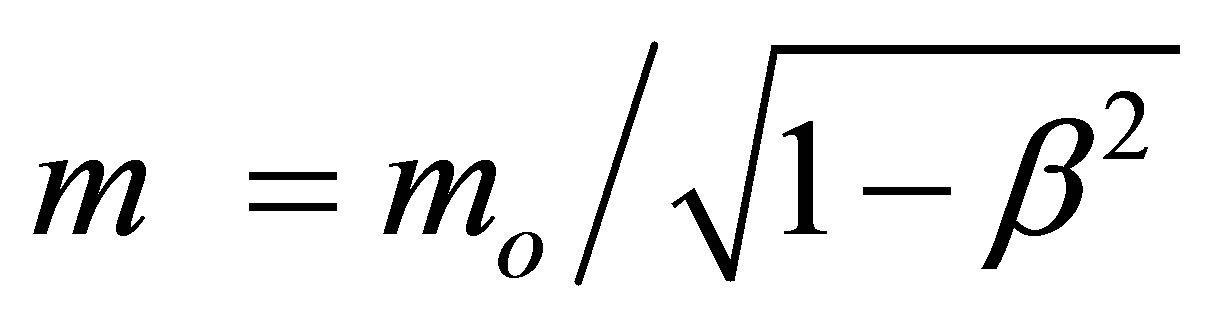 (7)
(7)
is slightly controversial [7] for the reasons explained by leading experts on the subject [6-8,25,27]. Second, and this includes our first point, we could extend E of special relativity to an EQR for quantum relativity, i.e. effective quantum gravity [8-14] by replacing c2 by the light cone velocity squared times c2
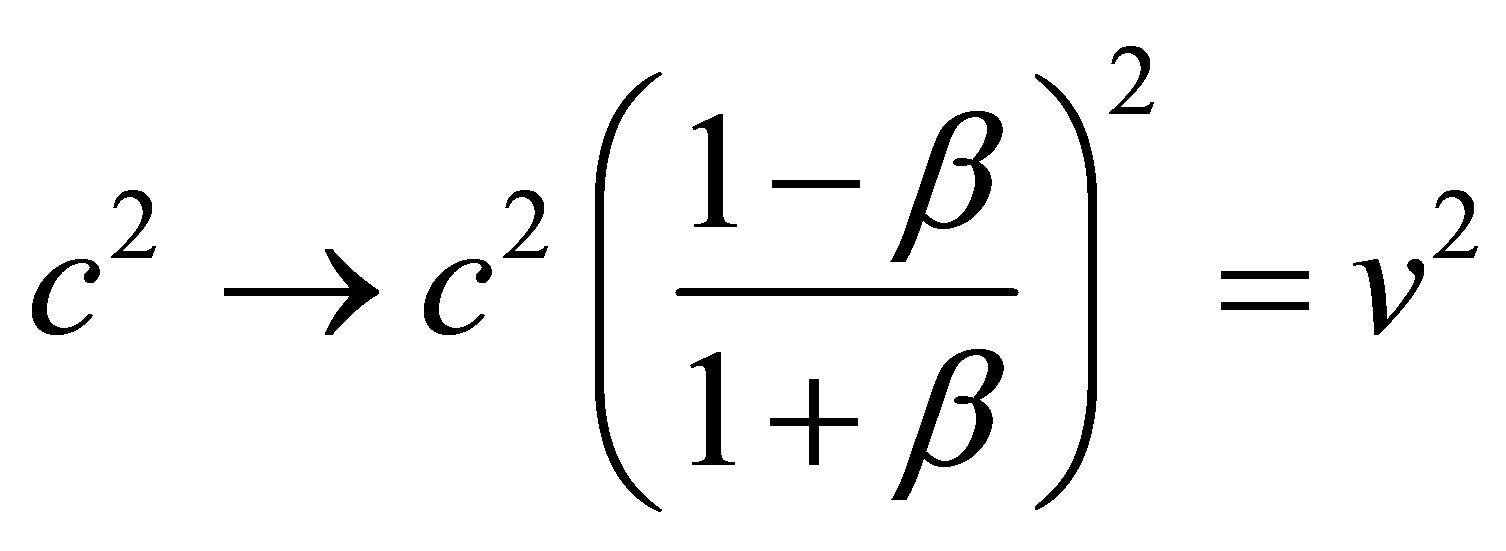 . (8)
. (8)
This then leads to a second replacement, namely that of the relativistic mass. However on the light cone we must exclude imaginary Lorentzian parameters while accepting infinite light cone velocity as in Newtonian classical mechanics [5]. Consistency then leads to the removal of the square root and we have
 (9)
(9)
which resembles certain aspects of the work on VSL theory pioneered by Moffat and Magueijo [8,25,33] as well as the author’s recent work [15-17]. Now our new energy mass equation
 (10)
(10)
is found from using Newton’s kinetic energy as a template
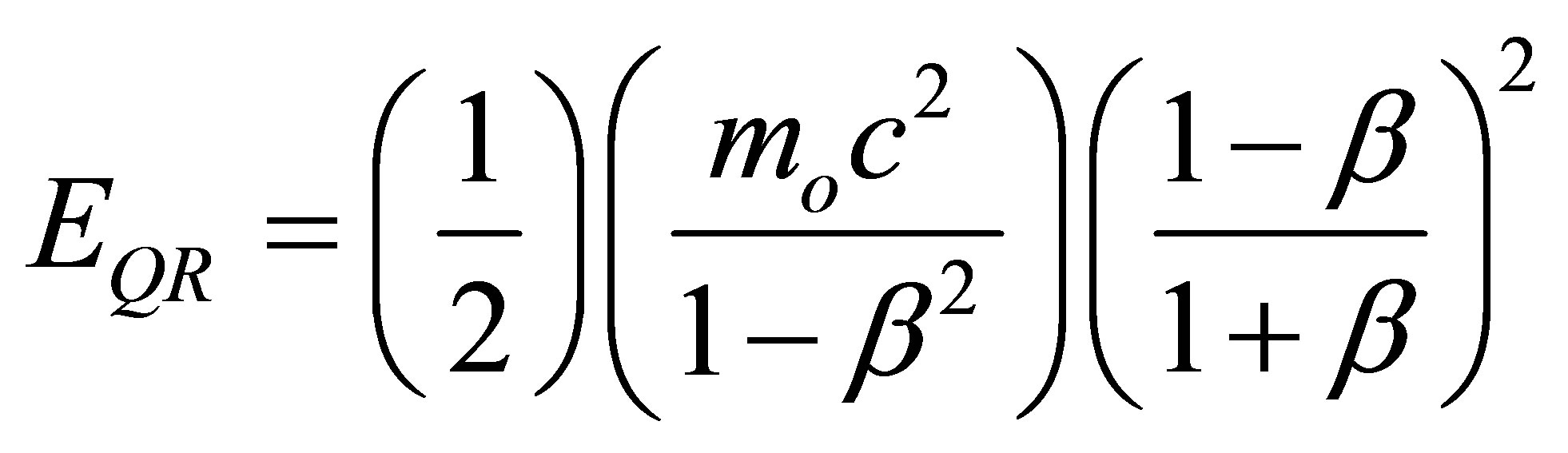 (11)
(11)
where mo is the truly rest mass [6-8]. Note that our derivation amounts to a de facto unified equation for classical relativistic and quantum mechanics [8-17]. The next decisive step is choosing the critical velocity parameter β which we do next.
4. Einstein’s Scaled Quantum Relativity Equation-Interpretation of the Result
If we contemplate the deep meaning of the EQR equation obtained in the previous section, then we easily realize it is a simple direct scaling of Einstein’s classical formula with a scaling factor [14,16]
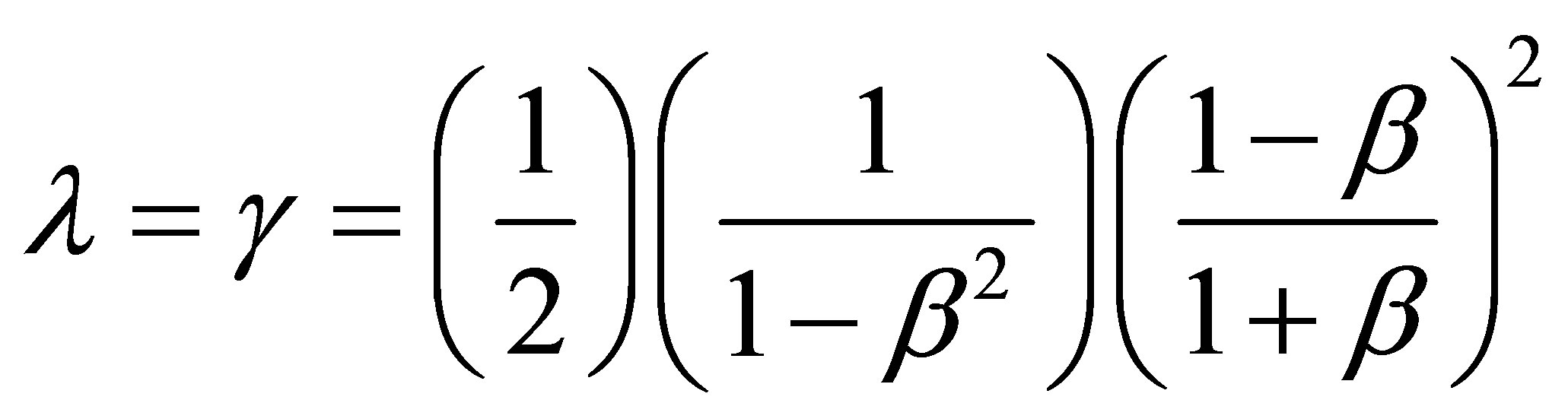 . (12)
. (12)
Suppose we set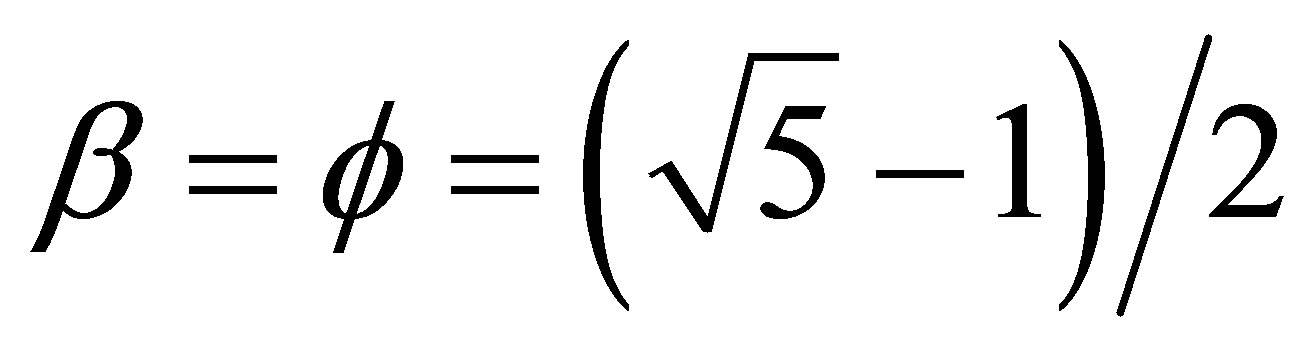 . That way we find
. That way we find
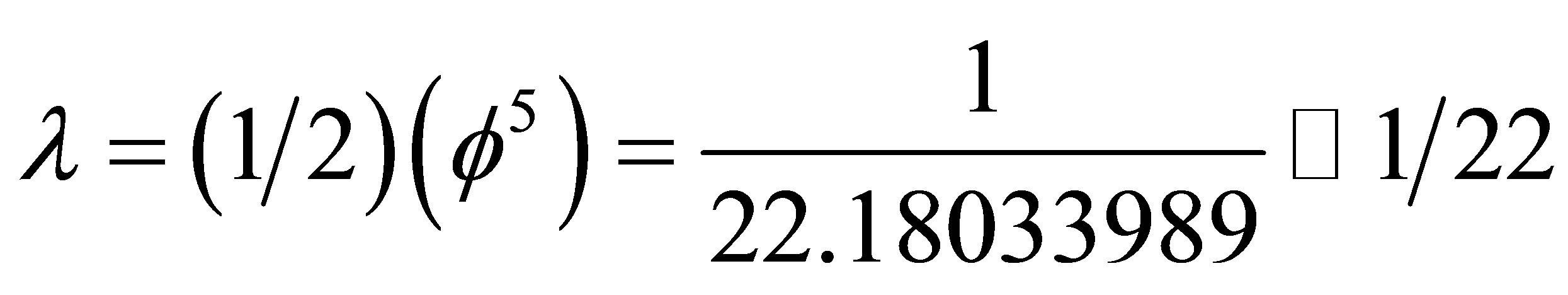 (13)
(13)
Consequently EQR which turned out to be identical to the ordinary measurable energy of the quantum particle E(O) is given by [15-18]
 . (14)
. (14)
This looks first innocent and second arbitrary. However it is neither the one nor the other. From a particle physics point of view and a Lagrangian which Einstein neither used nor established for the special theory of relativity although it is quite easily done [25], the scaling  says really that it is a quotient between a theory based on only 4 spacetime dimensions represented by a single degree of freedom, namely the photon compared to a more comprehensive theory represented by 22 dimensions left after extracting four i.e. 26 − 4 = 22. This may be regarded constructively as being Veneziano’s hidden dimensions [9] which as is well known, eliminate the negative norms from his dual resonance model [10]. These 22 dimensions in turn could again be viewed as the 12 dimensions −1 = 11 of the standard model minus the photon 12 − 1 = 11 plus another 11 super symmetric partners of an N = 1 super symmetric standard model making (2) (11) = 22 degrees of freedom [10-13] for the quantum relativity of an effectively quantum gravity theory which we have in essence introduced here [15-17].
says really that it is a quotient between a theory based on only 4 spacetime dimensions represented by a single degree of freedom, namely the photon compared to a more comprehensive theory represented by 22 dimensions left after extracting four i.e. 26 − 4 = 22. This may be regarded constructively as being Veneziano’s hidden dimensions [9] which as is well known, eliminate the negative norms from his dual resonance model [10]. These 22 dimensions in turn could again be viewed as the 12 dimensions −1 = 11 of the standard model minus the photon 12 − 1 = 11 plus another 11 super symmetric partners of an N = 1 super symmetric standard model making (2) (11) = 22 degrees of freedom [10-13] for the quantum relativity of an effectively quantum gravity theory which we have in essence introduced here [15-17].
In other words scale relativity principle or the original gauge theory of H. Weyl converted 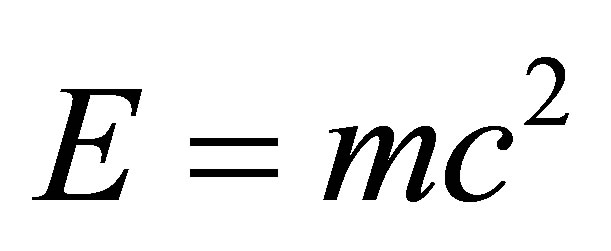 of special relativity to a formula which accounts for quantum mechanics via Hardy’s quantum entanglement for one particle
of special relativity to a formula which accounts for quantum mechanics via Hardy’s quantum entanglement for one particle 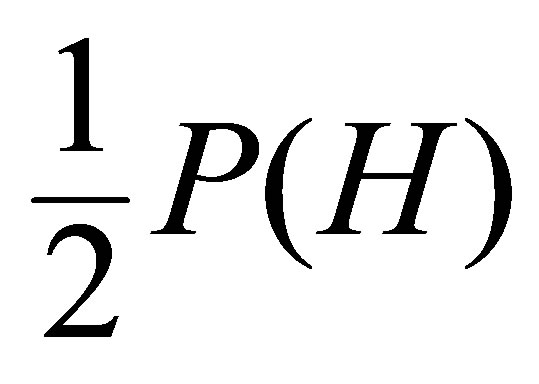 =
=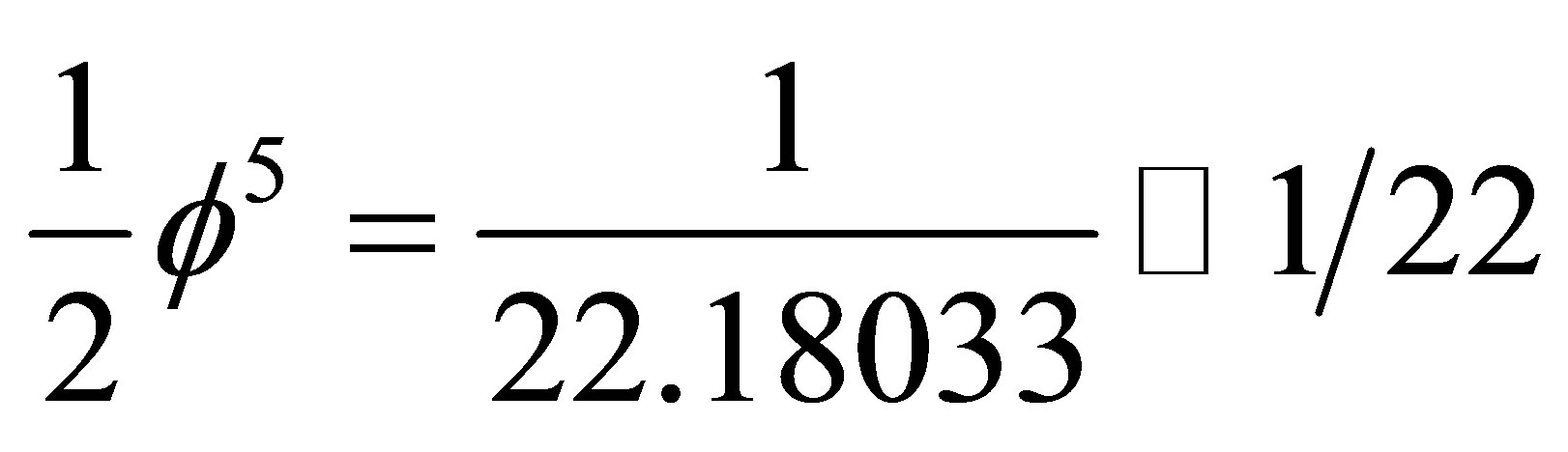 [15-17]. This formula now predicts that we have exactly
[15-17]. This formula now predicts that we have exactly
 (15)
(15)
hypothetical dark energy [3,4], in a figure of speech, hiding inside the 22 dark dimensions of the rugged Calabi-Yau-like manifold [18] of quantum relativity as opposed to the smooth 4 dimensional spacetime of special relativity [12,13]. Recent advances in understanding Equation (15) resulted in the profound realization that dark energy is the energy density of the Hawking-Hartle quantum wave of the universe as modelled by the empty set in five dimensional Kaluza-Klein spacetime [20] and is given by [21,22]
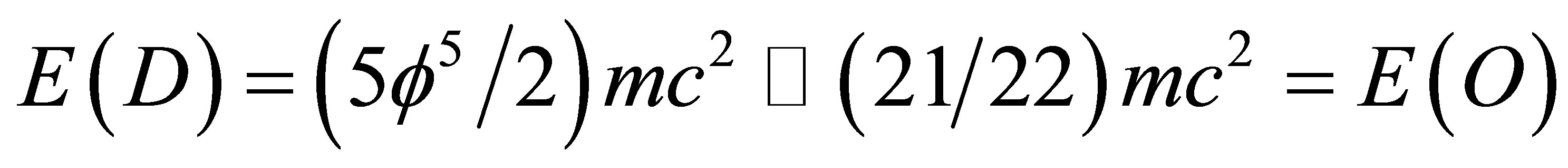 (16)
(16)
as shown previously [15-18]. As we already hinted at earlier on, this dark energy is effectively the absolute value of the negative energy stored in the five dimensional empty set modelling the quantum wave [15]. However things may be far more subtle and the quantum wave is just another picture of a KAM like quantum spacetime [19].
5. Relativistic Boost Derivation of 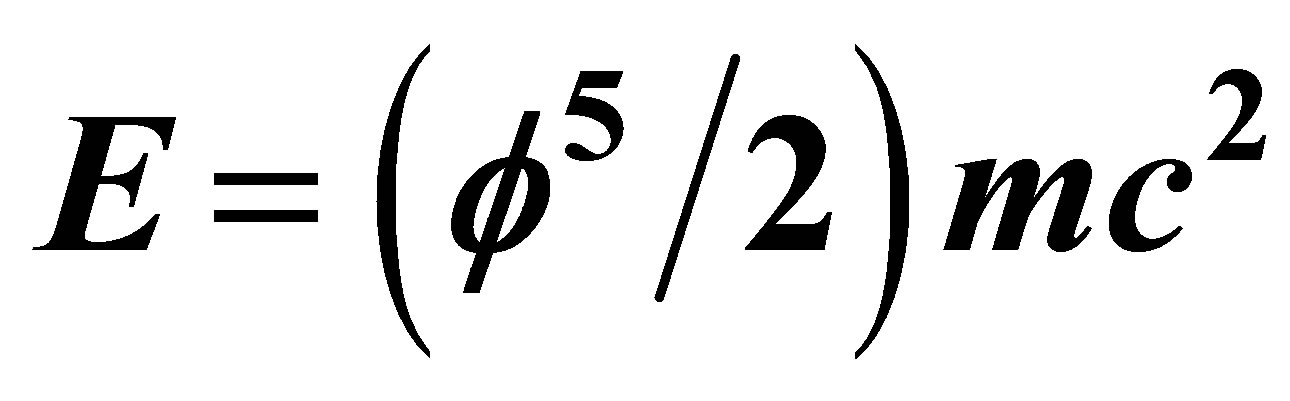
The following derivation may seem at first sight to be ad hoc and heuristic but it is much deeper than that (see Table 1). We start by introducing the three main phenomenological consequences of relativity via a boost and anti-boost transformation as the velocity tends to that of the speed of light, namely [6,24]
 (17)
(17)
and
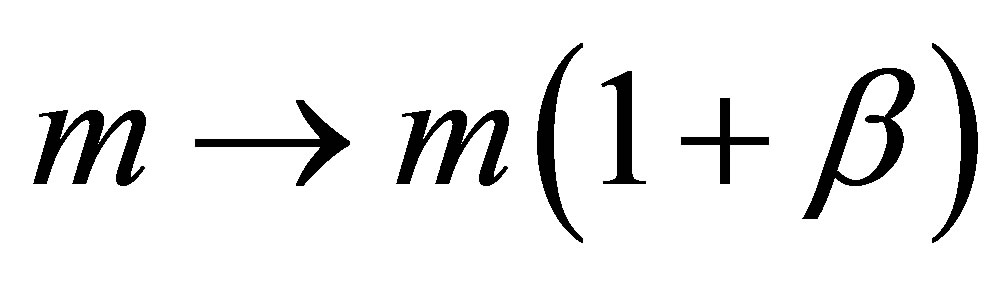 (i.e. mass increase)
(i.e. mass increase)

Table 1. Comparison between light cone derivation and relativistic boost derivation of .
.
Using Newton’s kinetic energy as a template we find
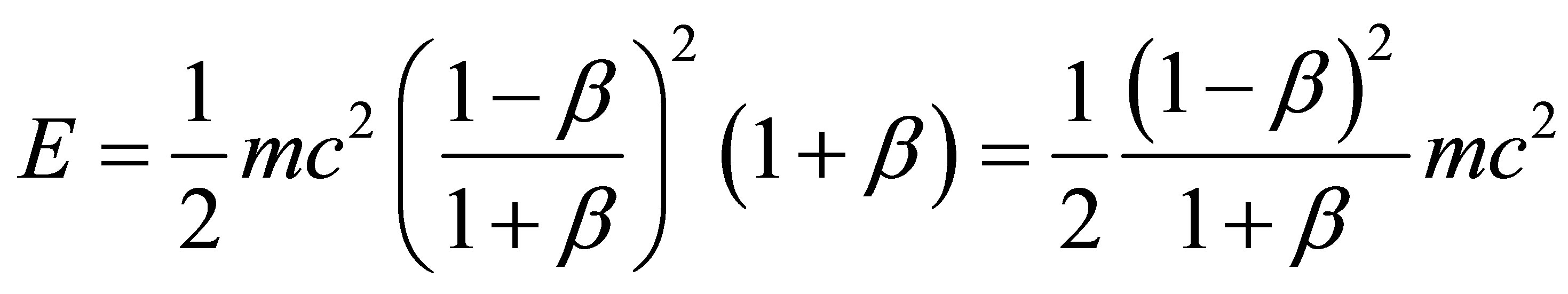 . (18)
. (18)
Equating Equation (18) to that of the light cone analysis (11) one finds
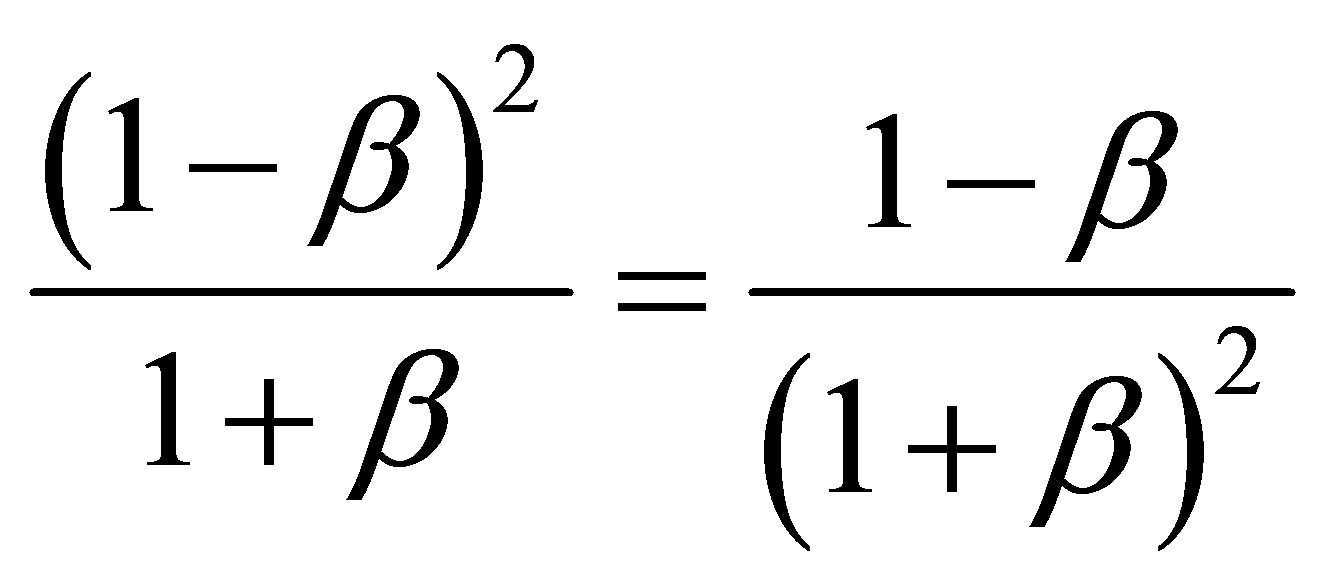 . (19)
. (19)
This gives us a quadratic equation in with the expected solution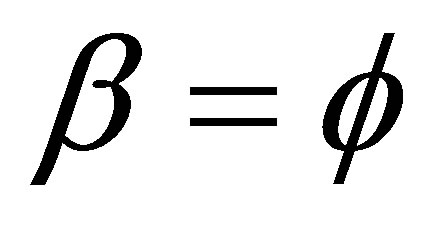 . Inserting back in (18) we find our anticipated result
. Inserting back in (18) we find our anticipated result . In Table 1 the two approaches are compared.
. In Table 1 the two approaches are compared.
6. Scaling the Planck scale and Arriving at the Missing Dark Energy Equations
In this section we set out to take seriously the extraordinarily inspiring and stimulating title of an article by D. Gross [26] “Can we scale the Planck scale?” by answering with yes and we do precisely that here [26,27].
Our starting point is naturally enough the BiedenharnHurwitz conjecture about “a meta time space with no a priori scale for a single path” [28,29]. This requirement is completely fulfilled in a Cantorian spacetime fractal [29- 31]. We then move on one more step by reducing our spacetime to a single unit interval random Cantor set and its complement [21-24]. The “speed” of this Cantorian unit interval universe will vary between zero and infinity where infinity corresponds to one which is joined back to zero in a unit circle following the fundamental equation of the continuum, namely zero equals one divided by infinity [16]. It can then be shown that while the arithmetic mean for the velocity in such an interval is 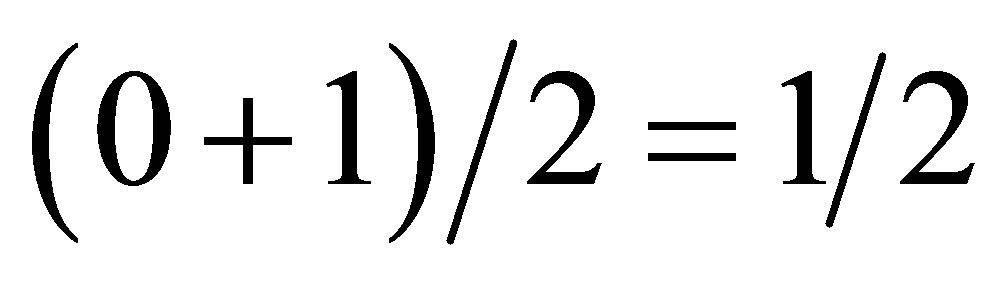 , the situation is different here because one corresponds to
, the situation is different here because one corresponds to  so that a Cantorian weight arithmetic mean shows that the average unit interval Cantorian speed is equal to the topological probability of finding the meta movement of a Cantorian point anywhere in the Cantorian set, namely
so that a Cantorian weight arithmetic mean shows that the average unit interval Cantorian speed is equal to the topological probability of finding the meta movement of a Cantorian point anywhere in the Cantorian set, namely  which is nothing but the Hausdorff dimension of this set [30,31]. The third step is to compute the resultant velocity for a five dimensional unit hyper cube. This is obviously a simple application of the extended theorem of Pythagoras
which is nothing but the Hausdorff dimension of this set [30,31]. The third step is to compute the resultant velocity for a five dimensional unit hyper cube. This is obviously a simple application of the extended theorem of Pythagoras
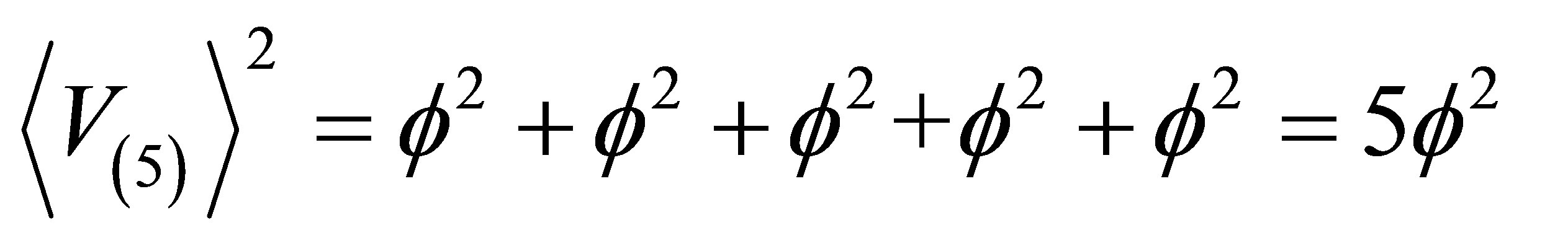 . (20)
. (20)
That way we could define 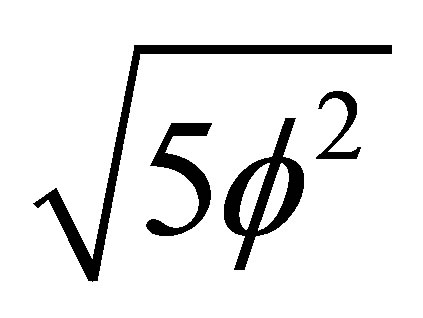 as the average topological velocity of light in five dimensional unit ball spacetime. However it is better to interpret this result in a more instructive way as a topological energy where the mass is a five dimensional m = 5 topological mass and
as the average topological velocity of light in five dimensional unit ball spacetime. However it is better to interpret this result in a more instructive way as a topological energy where the mass is a five dimensional m = 5 topological mass and 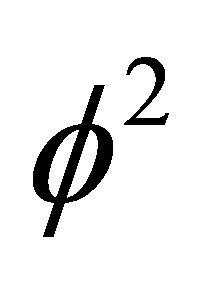 is the square of the velocity of light. Consequently we have [12,13,28,29]
is the square of the velocity of light. Consequently we have [12,13,28,29]
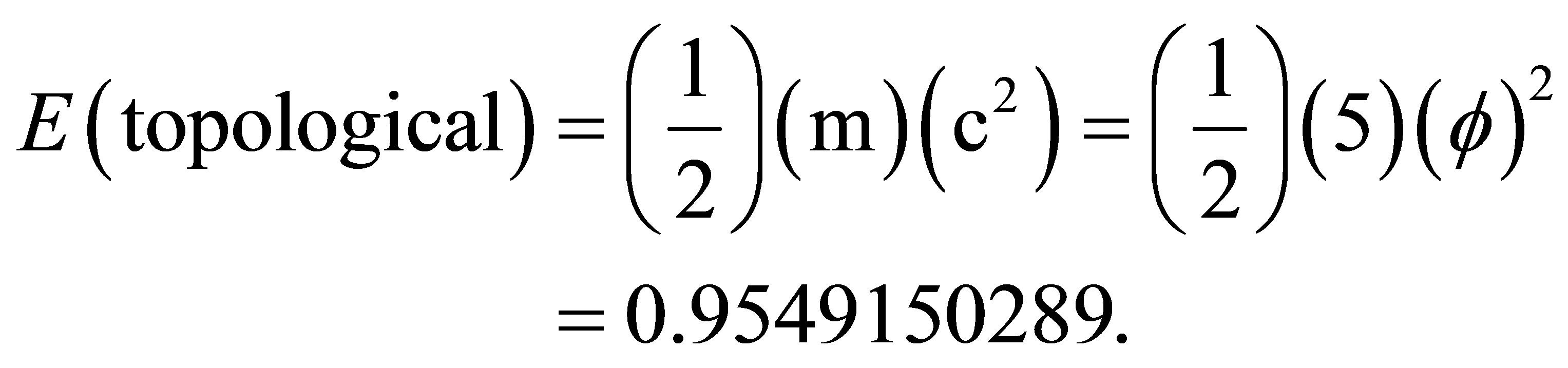 (21)
(21)
Comparing this result with that obtained using quantum relativity theory of entanglement we see that E(topological) is the exact dark energy density of the cosmos which is in astonishing agreement with recent cosmological measurements [3,4,17]. The ordinary energy density is consequently equal to 1 − (0.954150289) = 0.04508497107. This is exactly equal  and since the energy of quantum relativity is given for ordinary energy by the multiplication of Newton’s kinetic energy for
and since the energy of quantum relativity is given for ordinary energy by the multiplication of Newton’s kinetic energy for 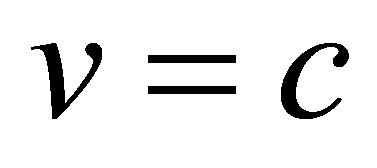 with Hardy’s generic probability of quantum entanglement
with Hardy’s generic probability of quantum entanglement  we see that
we see that  is the topological Planck energy
is the topological Planck energy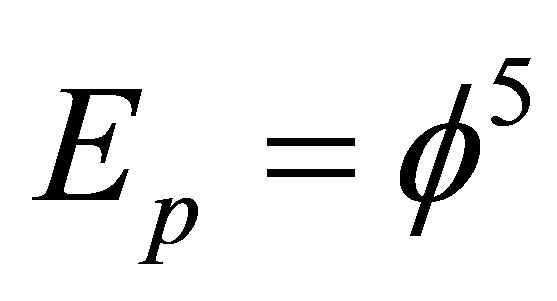 . In other words we have indeed scaled the Planck scale [26,27].
. In other words we have indeed scaled the Planck scale [26,27].
7. A Hint towards a Topological Unit Interval Cantorian Field Theory
From elementary considerations of what may be labelled, following D. Gross [26], “scaling the Planck scale” we are led slowly but surely to consider in earnest a topological unit interval Cantorian-fractal field theory which goes even deeper than modern topological field theories [32] in finding the most elementary basic elements of space, time and matter [29,30].
Let us start here by looking closely at what we have termed the topological speed of light [16]. In general velocity is a ratio between distance and time. However in our unit interval we have only a zero set and an empty set [15,17]. The zero set is measure zero and has a topological dimension equal zero so it can serve only as particles by virtue of its positive Hausdorff dimension 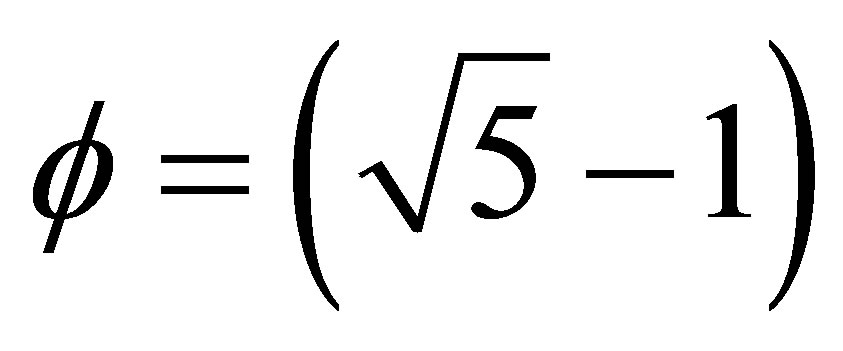 [12,19,23]. On the other hand the empty set has a positive measure 1 and a Hausdorff dimension
[12,19,23]. On the other hand the empty set has a positive measure 1 and a Hausdorff dimension  while the topological dimension is by inductive definition equal to −1 [12,21]. Thus the empty set could model a quantum wave or even much simpler, could model spacetime itself. Because we have really almost nothing in our spacetime interval, we paradoxically gain a new freedom of introducing meta time following BiedenharnHurwitz conjecture [3,4,6] and utilize the zero set for this purpose. Consequently our topological velocity or meta velocity of light replaces L/t by
while the topological dimension is by inductive definition equal to −1 [12,21]. Thus the empty set could model a quantum wave or even much simpler, could model spacetime itself. Because we have really almost nothing in our spacetime interval, we paradoxically gain a new freedom of introducing meta time following BiedenharnHurwitz conjecture [3,4,6] and utilize the zero set for this purpose. Consequently our topological velocity or meta velocity of light replaces L/t by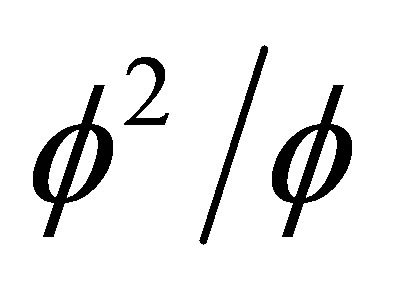 , i.e. space divided by non-space. That way we justify our weighted average or expectation value of the speed of light by setting
, i.e. space divided by non-space. That way we justify our weighted average or expectation value of the speed of light by setting
 (22)
(22)
Noting that  is a Hausdorff dimension, it is clearly related to entropy and consequently to energy [12,15]. It is thus understandable that we will have two methods of combining these entropies, namely additive entropy which applies to the empty “spacetime” sets and the multiplicative entropy which applies to the “particle” zero sets [22]. Thus in case of the empty set spacetime we obtain our energy by noting that we have
is a Hausdorff dimension, it is clearly related to entropy and consequently to energy [12,15]. It is thus understandable that we will have two methods of combining these entropies, namely additive entropy which applies to the empty “spacetime” sets and the multiplicative entropy which applies to the “particle” zero sets [22]. Thus in case of the empty set spacetime we obtain our energy by noting that we have
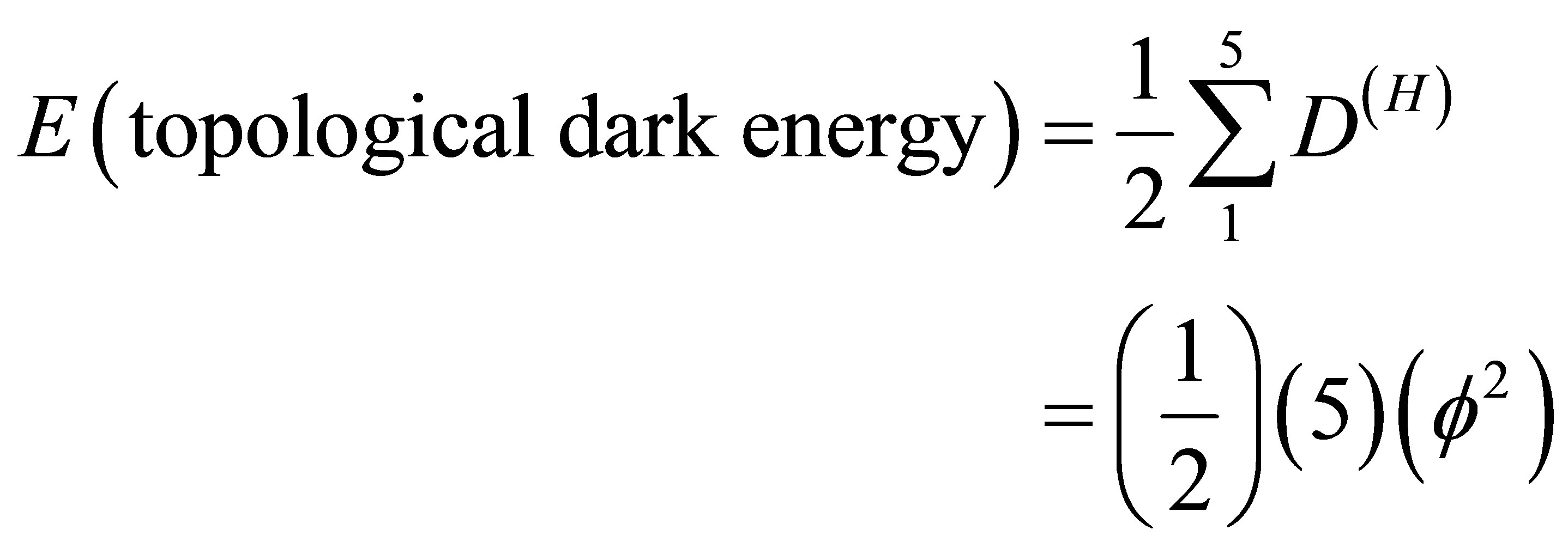 (23)
(23)
By dual complementarity to the above, multiplicative entropy leads to
 (24)
(24)
which is exactly the density of ordinary energy of the universe obtained previously using various methods [24]. Thus we could say that our unit interval field theory is quite powerful exactly because of the very limited number of variables and pure numbers which in turn embrace the universe as follows: The cobordism of the zero set is the empty set and the bordism of the empty set is the zero set. Thus we have:
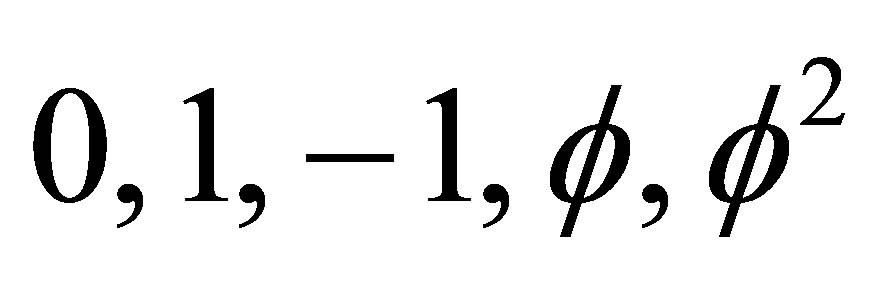 (25)
(25)
to work with. This gives us 0, 1 (Bernoulli processes)
0, 1, −1 (anti-Bernoulli processes)
 (being irrational it has all numbers in its decimal expansion)
(being irrational it has all numbers in its decimal expansion)
5 (because  and leads to Kaluza-Klein spacetime)
and leads to Kaluza-Klein spacetime)
One/infinity = zero (which is the most fundamental equation related to the continuum problem and ultimate L logic)[16].
This turned out to be all what is required for a general unified field theory at this level of description using nothing but a Cantorian unit interval and its complement. Now the road is wide open to further unsuspected topological constants, the most important of which is undoubtedly the theoretically and experimentally well established Hardy’s generic probability of quantum entanglement . It is easily shown that this is the largest topological energy possible which corresponds to Planck energy. Thus we deduce from
. It is easily shown that this is the largest topological energy possible which corresponds to Planck energy. Thus we deduce from  that the topological Planck energy is a five dimensional “unit hyper cube” energy equal to
that the topological Planck energy is a five dimensional “unit hyper cube” energy equal to
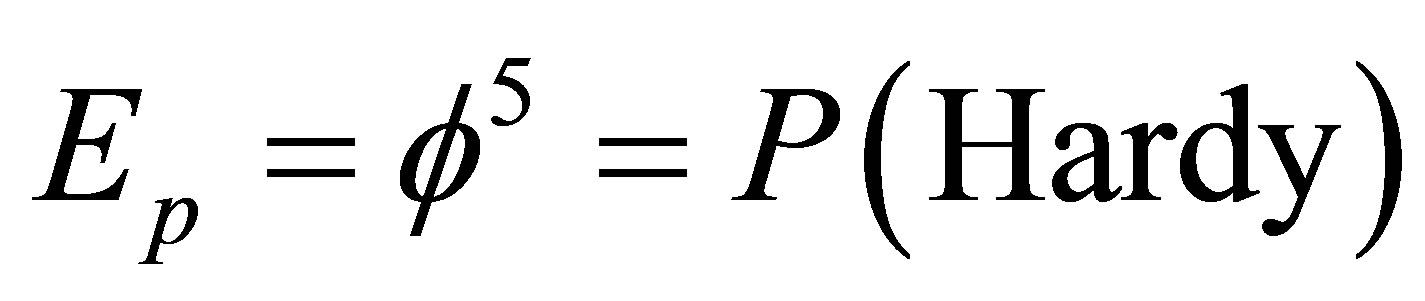 . (26)
. (26)
Now comes another unsuspected topological constant, namely the smallest possible which is the Planck quantum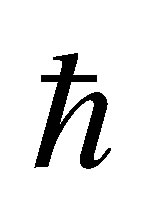 . Since in our circular unit interval
. Since in our circular unit interval  meets zero, then by an extended T-duality
meets zero, then by an extended T-duality 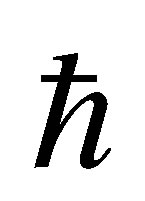 meets Ep and we have [10,16]
meets Ep and we have [10,16]
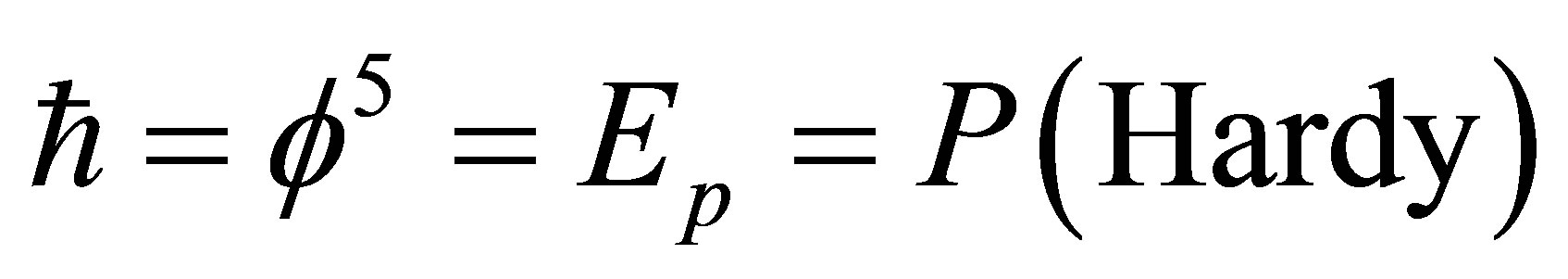 . (27)
. (27)
Maybe we should recall that in natural units the Planck energy is given by [5,10]
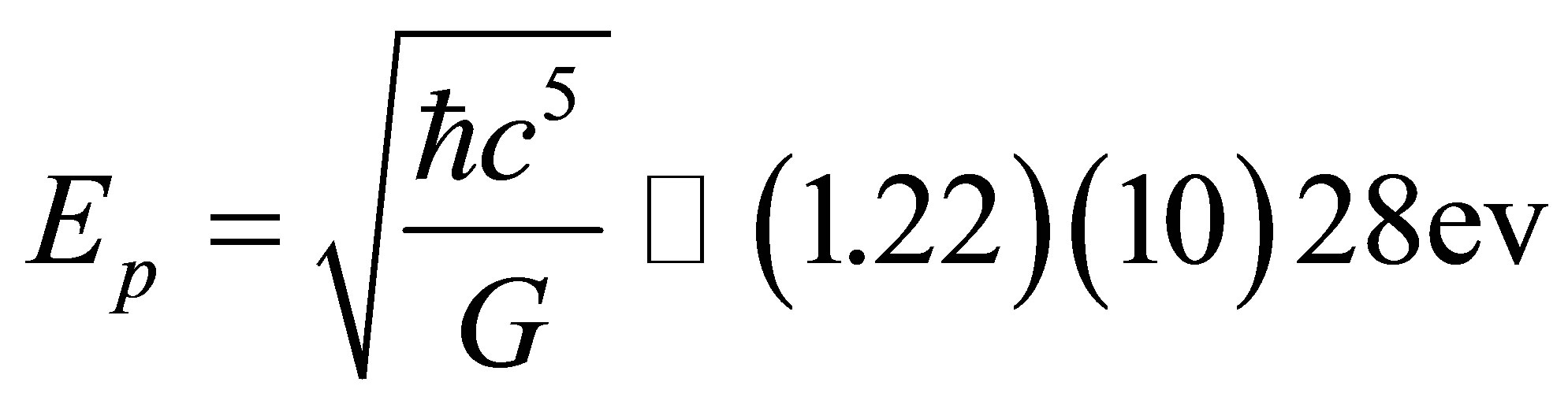 . (28)
. (28)
Setting 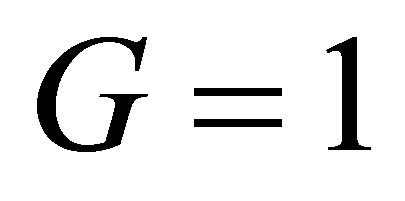 and inserting
and inserting 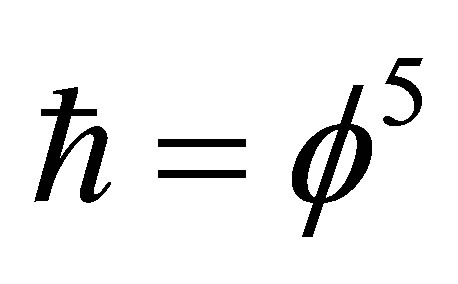 and
and 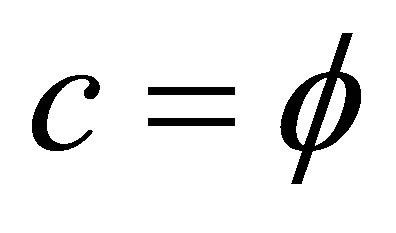 we find our topological Planck energy to be
we find our topological Planck energy to be
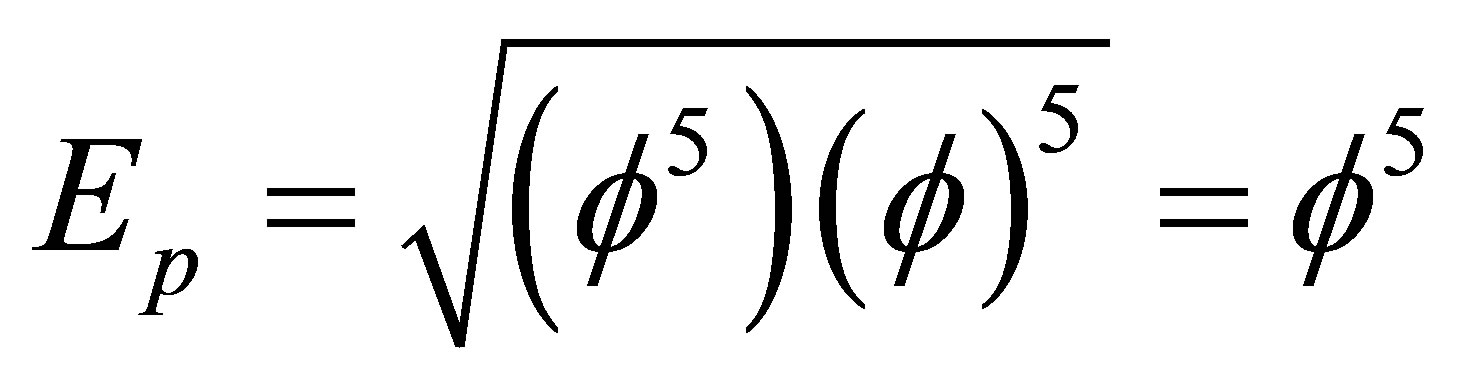 (29)
(29)
exactly as expected. There are still two values of importance, namely the topological mass for ordinary energy of the particle and that for dark energy of the wave. This is easily reasoned to be
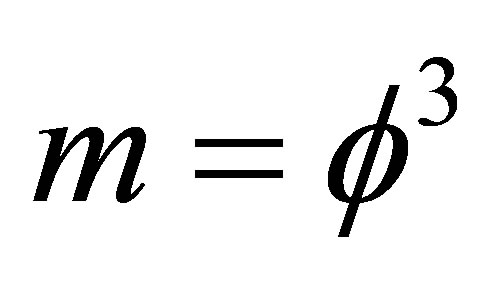 for the particle (where
for the particle (where 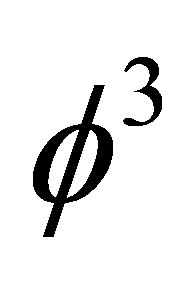 could be regarded as Unruh temperature [16] or the fractal part of
could be regarded as Unruh temperature [16] or the fractal part of  spacetime Hausdorff dimension)
spacetime Hausdorff dimension)
and
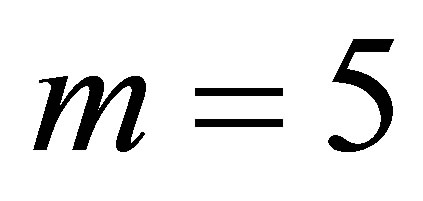 for the wave (where 5 may be regarded as the dimensionality of a Kaluza-Klein particle).
for the wave (where 5 may be regarded as the dimensionality of a Kaluza-Klein particle).
Insisting upon particle and wave simultaneously gives us  and consequently we retrieve Einstein’s total energy from [24,25]
and consequently we retrieve Einstein’s total energy from [24,25]
 (30)
(30)
in full agreement with previous derivations using different mathematical avenues.
We conclude that taking seriously Gross’ proposal to scale the Planck scale [26] is an imaginative idea which is quite real and which leads to fantastic simplification in solving truly complex problems. The idea is fully justified at the beginning by the fractal nature of spacetime expressed by Biedenharn-Hurwitz conjecture and at the end by producing the correct results of quantum gravity and quantum cosmology [12-17,21-25].
8. Conclusion
At the quantum level, gravity is normally too weak to affect things in a major way, exactly as quantum effects are of no great concern for the large scale structure of the cosmos [13,14]. That used to be the conventional wisdom [8,10,17]. However, as we started thinking about unification of all fundamental forces and similar deep and foundational issues of theoretical physics, we realized that at extremely small scales [13,14]. Gravity becomes very strong again compared to the other forces and somewhere at the Planck length all the coupling constants unify to only one [10-13]. As far as the issue of the hypothetical missing dark energy, the situation may not be dissimilar and essentially obeys Witten’s T-duality [16]. At extremely large scales comparable with the Hubble length scale [3,8], quantum mechanics and high energy particle physics become extremely important for relativity and gravity [16]. This is why one degree of freedom, single photon theory such as Einstein’s special relativity could not correctly predict the ordinary total detectable energy density in the cosmos. To do that, we need to include quantum entanglement or use more comprehensive theories such as string theory with 26 dimensions, superstrings with ten dimensions and M-theory with eleven dimensions [5,11,13]. Although the task of developing such a theory seems daunting, we could bypass much of these problems by concentrating on E = mc2 which we suspect to harbor the core of the trouble in all attempts towards a unified quantum gravity theory [8,25]. Since energy is the most basic and abstract notion in physics, it is not surprising that rescaling E to EQR of an effective quantum gravity theory [12] is simpler than expected because of an intrinsic self similarity on the level of the energy-mass equation as is trivially obvious from the Newtonian kinetic energy 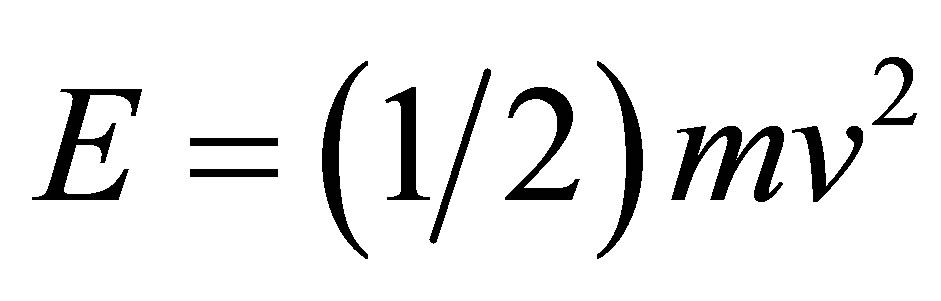 and the famous equation of special relativity E = mc2 [24]. The crux of the matter is that spacetime of relativity is smooth, connected and has only 4 dimensions. However to model real spacetime at extremely small or by T-duality extremely large scales, a complex, rugged and multidimensional manifold is needed, for instance, a CalabiYau manifold with 6 real dimensions [15] or a K3 Kähler manifold with 4 complex dimensions. Ord-Nottale fractal spacetime [13,14] and Cantorian spacetime are other options [13,14]. Using all these different theories, we arrive at the same robust formula which predicts that
and the famous equation of special relativity E = mc2 [24]. The crux of the matter is that spacetime of relativity is smooth, connected and has only 4 dimensions. However to model real spacetime at extremely small or by T-duality extremely large scales, a complex, rugged and multidimensional manifold is needed, for instance, a CalabiYau manifold with 6 real dimensions [15] or a K3 Kähler manifold with 4 complex dimensions. Ord-Nottale fractal spacetime [13,14] and Cantorian spacetime are other options [13,14]. Using all these different theories, we arrive at the same robust formula which predicts that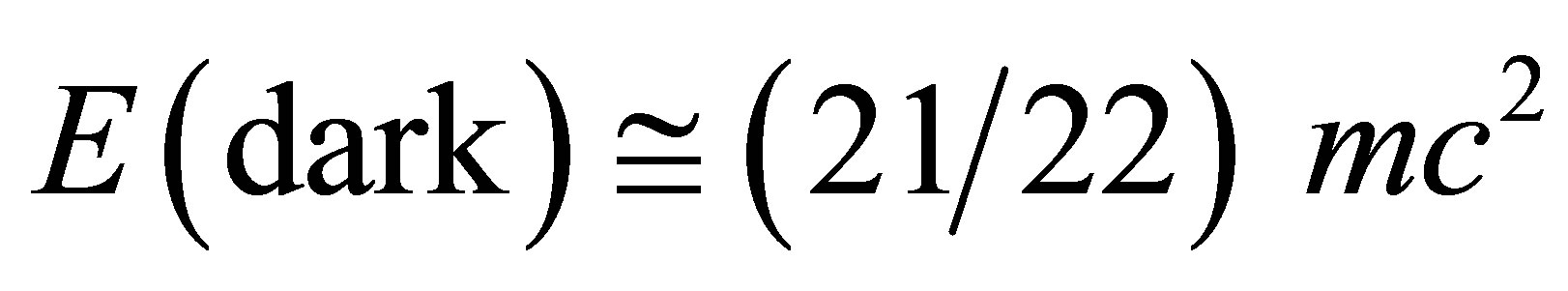 , i.e. almost 95.5% of the energy density of the cosmos is either not there at all or is hiding within the 22 hidden dimensions or fractal voids of spacetime and totally inaccessible to measurement [15-17]. It is mathematically very easy to reason why E(Dark) is not acessible to measurement. It is because dark energy is the energy of a five dimensional Kaluza-Klein empty set with a negative topological dimension and
, i.e. almost 95.5% of the energy density of the cosmos is either not there at all or is hiding within the 22 hidden dimensions or fractal voids of spacetime and totally inaccessible to measurement [15-17]. It is mathematically very easy to reason why E(Dark) is not acessible to measurement. It is because dark energy is the energy of a five dimensional Kaluza-Klein empty set with a negative topological dimension and 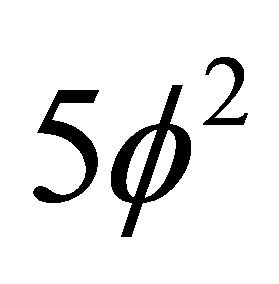 Hausdorff dimension which models the quantum wave [17]. Since measurement collapses the quantum wave, dark energy cannot be detected in a direct way. In fact, the quantum wave in view of KAM theorem [19] may be quantum spacetime itself [15]. This is possibly the more profound explanation for why we cannot find dark energy which is the very act of cosmic measurement itself which collapses the quantum Hawking-Hartle wave of the universe which harbours cosmic dark energy [23]. The present theoretical prediction, namely that ordinary energy is the energy of the quantum particle and amounts to only 4.5% of the total energy density while dark energy is the energy of the quantum wave and amounts to 95.5% is quantitatively in astonishing agreement with cosmological measurements [3,4]. It speaks volumes about the basic correctness of the theoretical underpinning of the present theory that E(O) + E(Dark) = mc2 = E(Einstein) [15-18] as well as the fact that
Hausdorff dimension which models the quantum wave [17]. Since measurement collapses the quantum wave, dark energy cannot be detected in a direct way. In fact, the quantum wave in view of KAM theorem [19] may be quantum spacetime itself [15]. This is possibly the more profound explanation for why we cannot find dark energy which is the very act of cosmic measurement itself which collapses the quantum Hawking-Hartle wave of the universe which harbours cosmic dark energy [23]. The present theoretical prediction, namely that ordinary energy is the energy of the quantum particle and amounts to only 4.5% of the total energy density while dark energy is the energy of the quantum wave and amounts to 95.5% is quantitatively in astonishing agreement with cosmological measurements [3,4]. It speaks volumes about the basic correctness of the theoretical underpinning of the present theory that E(O) + E(Dark) = mc2 = E(Einstein) [15-18] as well as the fact that 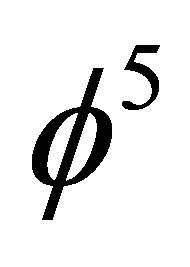 is Hardy’s probability of quantum entanglement which means that
is Hardy’s probability of quantum entanglement which means that 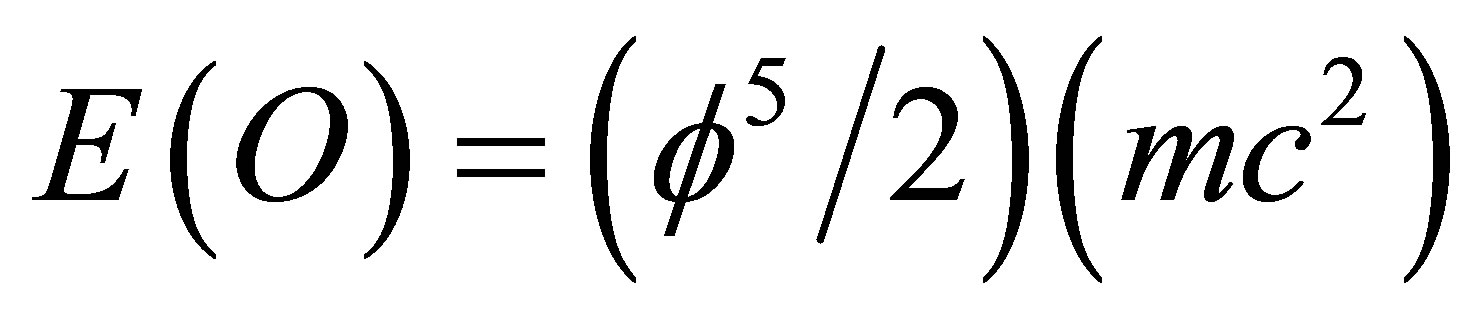 is an intersectional equation for quantum relativity unifying the view point of both theories [21,22]. Finally we put the entire present analysis in a wider perspective and more fundamental basis by treading the road outlined in D. Gross’ article regarding scaling the Planck scale [26]. The preceding results could be expressed succinctly in a few words in terms of the language of microphysics to mean that cosmic wormholes are created by Einstein-Podolsky-Rosen quantum entanglement of the Hardy type which changes the geometry of cosmic spacetime at the micro resolution to a zero measure Cantorian fractal [15-24,34].
is an intersectional equation for quantum relativity unifying the view point of both theories [21,22]. Finally we put the entire present analysis in a wider perspective and more fundamental basis by treading the road outlined in D. Gross’ article regarding scaling the Planck scale [26]. The preceding results could be expressed succinctly in a few words in terms of the language of microphysics to mean that cosmic wormholes are created by Einstein-Podolsky-Rosen quantum entanglement of the Hardy type which changes the geometry of cosmic spacetime at the micro resolution to a zero measure Cantorian fractal [15-24,34].
REFERENCES
- L. Sigalotti and A. Mejias, “The Golden Mean in Special Relativity,” Chaos, Solitons & Fractals, Vol. 30, No. 3, 2006, pp. 521-524. doi:10.1016/j.chaos.2006.03.005
- S. Hendi and M. Sharif Zadeh, “Special Relativity and the Golden Ratio,” Journal of Theoretical Physics, Vol. 1, 2012, pp. 37-45.
- L. Amendola and S. Tsujikawa, “Dark Energy: Theory and Observations,” Cambridge University Press, Cambridge, 2010.
- Nobel Foundation, “The Nobel Prize in Physics,” 2011. http://nobelprize.org.nobelprizes/physics/Laureates/2011/index.html
- B. Zwiebach, “A First Course in String Theory,” Cambridge University Press, Cambridge, 2004. doi:10.1017/CBO9780511841682
- W. Rindler, “Relativity,” Oxford Science Publications, Oxford, 2004.
- L. B. Okun, “Energy and Mass in Relativity Theory,” World Scientific, Singapore, 2009.
- J. Mageuijo and L. Smolin, “Lorentz Invariance with an Invariant Energy Scale,” arXiv: hepth/0112090V2.
- G. Veneziano, “An Introduction to Dual Models of Strong Interactions and Their Physical Motivations,” Physical Reports, Vol. C9, 1974, p. 199.
- M. Green, J. Schwarz and E. Witten, “Superstring Theory,” Cambridge University Press, Cambridge, 1994.
- B. Bavnbek, G. Esposito and M. Lesch, “New Paths towards Quantum Gravity,” Springer, Berlin 2010. doi:10.1007/978-3-642-11897-5
- M. S. El Naschie, “The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review),” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2635-2646. doi:10.1016/j.chaos.2008.09.059
- M. S. El Naschie, “A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 19, No. 1, 2004, pp. 209-236. doi:10.1016/S0960-0779(03)00278-9
- L. Nottale, “Scale Relativity and Fractal Space-Time,” Imperial College Press, London, 2011.
- M. S. El Naschie, “Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a ‘Halo’ Energy of the Schrödinger Quantum Wave,” Journal of Modern Physics, Vol. 4, 2013, pp. 591-596. doi:10.4236/jmp.2013.45084
- L. Marek-Crnjac, M. S. El Naschie and J.-H. He, “Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, pp. 78-88. doi:10.4236/ijmnta.2013.21A010
- M. S. El Naschie, “A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory,” Journal of Quantitative Information Science, Vol. 3, 2013, pp. 23- 26. doi:10.4236/jqis.2013.31006
- T. Hübsch, “Calabi-Yau Manifolds,” World Scientific, Singapore, 1992. doi:10.1142/1410
- J. Guckenheimer and P. Holmes, “Nonlinear Dynamical Systems and Bifurcation of Vector Fields,” Springer Verlag, New York, 1994.
- P. S. Wesson, “Five-Dimensional Physics,” World Scientific, Singapore, 2006.
- M. S. El Naschie, “A Fractal Menger Sponge Spacetime Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, pp. 107-121. doi:10.4236/ijmnta.2013.22014
- M. S. El Naschie, “Dark Energy from Kaluza-Klein Spacetime and Noether’s Theorem via Lagrangian Multiplier Method,” Journal of Modern Physics, Vol. 4, 2013, pp. 757-760. doi:10.4236/jmp.2013.46103
- M.S. El Naschie, “Quantum Entanglement: Where Dark Energy and Negative Gravity plus Accelerated Expansion of the Universe Comes from,” Journal of Quantitative Information Science, Vol. 3, No. 2, 2013, pp. 57-77. doi:10.4236/jqis.2013.32011
- M. S. El Naschie, “A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 1, 2013, pp. 43-54. doi:10.4236/ijmnta.2013.21005
- J. Magueijo, “Faster than the Speed of Light,” Arrow Books, London, 2003.
- D. Gross, “Can We Scale the Planck Scale?” Physics Today, Vol. 42, No. 6, 1989, p. 9.
- A. Albrecht and C. Skordis, “Phenomenology of a Realistic Accelerating Universe Using only Planck scale Physics,” arXiv: astro-ph/9908085V2
- L. Biedenharn and L. Horwitz, “Quantum Theory and Exceptional Gauge Groups,” Proceedings of Second John Hopkins Workshop, California, 21 April 1978.
- M. S. El Naschie, “Dimensional Symmetry Breaking, Information and Fractal Gravity in Cantorian Space,” Biosystems, Vol. 46, No. 1-2, 1998, pp. 41-46. doi:10.1016/S0303-2647(97)00079-8
- M. Crasmareanu and C. Hretcanu, “Golden Differential Geometry,” Chaos, Solitons & Fractals, Vol. 38, No. 5, 2008, pp. 1229-1238. doi:10.1016/j.chaos.2008.04.007
- M. S. El Naschie, “Fractal Gravity and Symmetry Breaking in Hierarchal Cantorian Space,” Chaos, Solitons & Fractals, Vol. 8, No. 11, 1997, pp. 1865-1872. doi:10.1016/S0960-0779(97)00039-8
- E. Witten, “Topological Quantum Field,” Communications in Mathematical Physics, Vol. 117, No. 3, 1988, pp. 353-386. doi:10.1007/BF01223371
- J. Mageuijo and J. Moffat, “Comments on “Note on Varying Speed of Light Theories,” arXiv:0705.4507V1[gr-9c]
- J. Maldacena and L. Susskind, “Cool Horizons for Entangled Black Holes,” 11 July 2013. arXiv: 1306.0533V2[hep-th]

