Open Journal of Microphysics
Vol.3 No.2(2013), Article ID:31731,9 pages DOI:10.4236/ojm.2013.32007
Search for High Energy Electrons from New Neutral Massive Gauge Boson Decay in the CMS Detector at the LHC Using Monte Carlo Simulation
Department of Physics, Faculty of Science, Cairo University, Giza, Egypt
Email: mansourhesham@yahoo.com, nady.bakhet@cern.ch, nady.bakhet@yahoo.com
Copyright © 2013 H. M. M. Mansour, Nady Bakhet. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 27, 2012; revised January 28, 2013; accepted February 6, 2013
Keywords: LHC; CMS; Monte Carlo Simulation; New Boson; SM; B-L; Gauge Boson
ABSTRACT
The existence of new heavy neutral massive boson Z′ is a feature of many extensions of Standard Model models as the two-Higgs-doublet model (2HDM), the Hidden Abelian Higgs Model (HAHM), Left-Right Symmetric Model (LRSM), Sequential Standard Model (SSM) and Baryon number minus Lepton number Model (B-L). In the present work we search for two high energy electrons produced from decaying  heavy neutral massive boson in the events produced in proton-proton collisions at LHC and can be detected by CMS detector. We used the data which is produced from proton-proton collisions by Monte Carlo events generator for different energies at LHC, then we use the angular distribution, invariant mass, combined transverse momentum and combined rapidity distributions for the two high energy electrons produced from
heavy neutral massive boson in the events produced in proton-proton collisions at LHC and can be detected by CMS detector. We used the data which is produced from proton-proton collisions by Monte Carlo events generator for different energies at LHC, then we use the angular distribution, invariant mass, combined transverse momentum and combined rapidity distributions for the two high energy electrons produced from 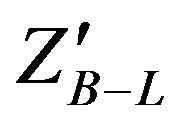 decay channel to detect the
decay channel to detect the  signal. B-L extension of the SM model predicts the existence of a
signal. B-L extension of the SM model predicts the existence of a 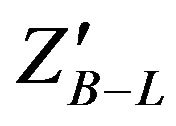 heavy neutral massive boson at high energies. From our results which we had simulated using MC programs for
heavy neutral massive boson at high energies. From our results which we had simulated using MC programs for  in the B-L extension of standard model, we predict a possible existence of new gauge
in the B-L extension of standard model, we predict a possible existence of new gauge  at LHC in the mass range 1 TeV to 1.5 TeV via electrons identification of the two high energy electrons by CMS detector.
at LHC in the mass range 1 TeV to 1.5 TeV via electrons identification of the two high energy electrons by CMS detector.
1. Introduction
The Standard Model (SM) of particles physics provides a good explanation for most known particles but there are several points need an answer, dark matter, dark energy, CP violation to explain the baryonic matter-antimatter asymmetry of the universe and finally neutrino oscillations. From that we can say the SM requires an extension. B-L model is an extension for the SM which is based on the gauge group [1-3] 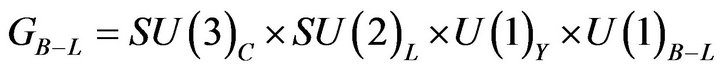 . The invariance of the Lagrangian under this gauge symmetry implies the existence of a new gauge boson (beyond the SM ones) and the spontaneous symmetry breaking in this model provides a natural explanation for the presence of three right-handed neutrinos in addition to an extra gauge boson and a new scalar Higgs. Therefore, it can lead to a very interesting phenomenology which is different from the SM results and it can be tested at the LHC.
. The invariance of the Lagrangian under this gauge symmetry implies the existence of a new gauge boson (beyond the SM ones) and the spontaneous symmetry breaking in this model provides a natural explanation for the presence of three right-handed neutrinos in addition to an extra gauge boson and a new scalar Higgs. Therefore, it can lead to a very interesting phenomenology which is different from the SM results and it can be tested at the LHC.
An extra neutral massive gauge boson corresponding to the B-L gauge symmetry is predicted. There are many models which contain extra gauge bosons. These models can be classified into two categories depending on whether or not they arise in a GUT scenario. In some of these models, 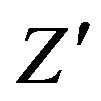 and SM Z are not true mass due to mixing. This mixing induces the couplings between the extra
and SM Z are not true mass due to mixing. This mixing induces the couplings between the extra  boson and the SM fermions.
boson and the SM fermions.
In the B-L extension of the SM model, the extra  boson and SM fermions are coupled through the nonvanishing B-L quantum numbers. Searching for
boson and SM fermions are coupled through the nonvanishing B-L quantum numbers. Searching for 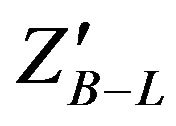 is accessible via a clean dilepton signal at LHC. We will simulate B-L extension of the SM at LHC which is based on the gauge group
is accessible via a clean dilepton signal at LHC. We will simulate B-L extension of the SM at LHC which is based on the gauge group  using MC programs then search for the
using MC programs then search for the 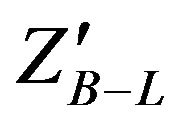 boson in the dielectron events produced in pp collisions at different energies of LHC where the leptonic decay
boson in the dielectron events produced in pp collisions at different energies of LHC where the leptonic decay 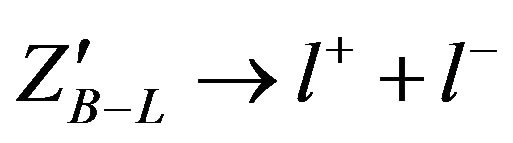 provides the most distinctive signature for observing the
provides the most distinctive signature for observing the  signal at the Large Hadron Collider. The results in this paper were produced by using simulation events generator PYTHIA8 [4-6] and other software tools as CalcHep, MadGraph/Madevent, FeynRules, ROOT data analysis, Physics Analysis Workstation (PAW), ROOFIT package to fit any resulted histogram in order to get P.D.F. (Probability density function) and Mathematica.
signal at the Large Hadron Collider. The results in this paper were produced by using simulation events generator PYTHIA8 [4-6] and other software tools as CalcHep, MadGraph/Madevent, FeynRules, ROOT data analysis, Physics Analysis Workstation (PAW), ROOFIT package to fit any resulted histogram in order to get P.D.F. (Probability density function) and Mathematica.
In this paper, the results are organized into three subsections. Firstly, we present the production of  at LHC which includes production cross section, different branching ratios and total width. Secondly, the detection of
at LHC which includes production cross section, different branching ratios and total width. Secondly, the detection of 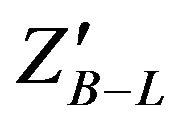 signal at LHC via the decay channel
signal at LHC via the decay channel  then we study the dielectron angular distribution, dielectron asymmetry, Drell Yan background events for this channel and dielectron invariant mass. Thirdly, we present the properties of
then we study the dielectron angular distribution, dielectron asymmetry, Drell Yan background events for this channel and dielectron invariant mass. Thirdly, we present the properties of 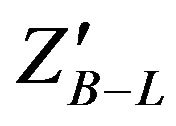 which include Luminosity, Significance, Transverse momentum and Rapidity.
which include Luminosity, Significance, Transverse momentum and Rapidity.
2. Results
In this section we present our results for production and detection of a 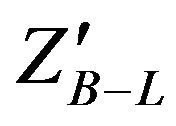 signal of the B-L extension of SM using MC programs [7,8]. We present the production cross section of
signal of the B-L extension of SM using MC programs [7,8]. We present the production cross section of 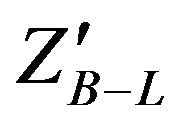 at LHC as a function of
at LHC as a function of  mass for various
mass for various 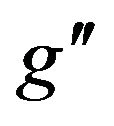 values (where
values (where 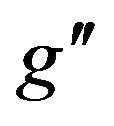 is the U(1)B–L gauge coupling constant) and for various energies at LHC, branching ratios as a function of
is the U(1)B–L gauge coupling constant) and for various energies at LHC, branching ratios as a function of  mass for heavy neutrino mass = 200 GeV which will affect the results of
mass for heavy neutrino mass = 200 GeV which will affect the results of 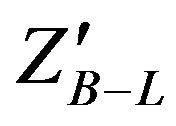 due to the fact that it is a heavy particle. We obtained different results in comparison with Ref [9]. The analysis in this paper did not take into account the existence of new decay channel for heavy neutrino in B-L model which is one of the important signatures of B-L model and they did not give any branching ratio for heavy neutrino. After that we will present
due to the fact that it is a heavy particle. We obtained different results in comparison with Ref [9]. The analysis in this paper did not take into account the existence of new decay channel for heavy neutrino in B-L model which is one of the important signatures of B-L model and they did not give any branching ratio for heavy neutrino. After that we will present 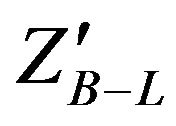 total width as a function of
total width as a function of 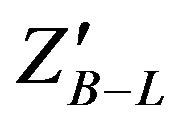 mass for various values of
mass for various values of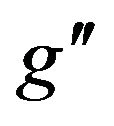 . Both angular distribution of dielectron and invariant mass of dielectron produced of
. Both angular distribution of dielectron and invariant mass of dielectron produced of  decay are used to detect
decay are used to detect  signal at LHC. Finally, we will focus on the properties of
signal at LHC. Finally, we will focus on the properties of  such as Luminosity, Significance, Transverse momentum and Rapidity.
such as Luminosity, Significance, Transverse momentum and Rapidity.
2.1. Production of  at LHC
at LHC
2.1.1. Production Cross Section
In Figures 1 and 2 we present the production cross section for 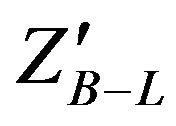 for the most relevant production mechanisms for different CM energies. Figure 1 gives the cross section for
for the most relevant production mechanisms for different CM energies. Figure 1 gives the cross section for 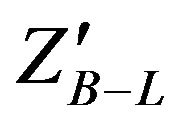 at LHC as a function of
at LHC as a function of  mass for various
mass for various 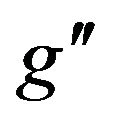 values (where
values (where 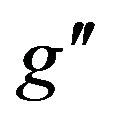 is the U(1)B.L gauge coupling constant) at CM energy of LHC = 14 TeV. Figure 2 gives cross sections for
is the U(1)B.L gauge coupling constant) at CM energy of LHC = 14 TeV. Figure 2 gives cross sections for 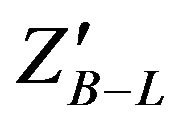 at LHC for CM energies √s = 5, 7, 10, 12, 14 TeV at fixed value of
at LHC for CM energies √s = 5, 7, 10, 12, 14 TeV at fixed value of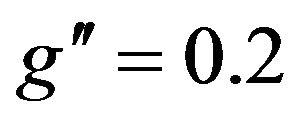 . At the patron level, the
. At the patron level, the  production cross section depends on two main parameters, the mass of
production cross section depends on two main parameters, the mass of 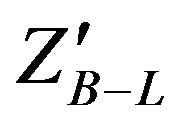 and the coupling constant
and the coupling constant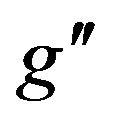 . Therefore, the B-L model is controlled by two parameters: the mass of the
. Therefore, the B-L model is controlled by two parameters: the mass of the  and the coupling constant
and the coupling constant  determining
determining  couplings.
couplings.
Two experimental constraints exist on these two parameters, the first comes from direct search for heavy neutral gauge bosons at the CDF experiment which excludes a 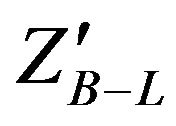 mass less than 600 GeV and the second limit comes from LEP II where:
mass less than 600 GeV and the second limit comes from LEP II where:
 (1)
(1)
The interactions of  boson with the SM fermions in B-L model is described by
boson with the SM fermions in B-L model is described by
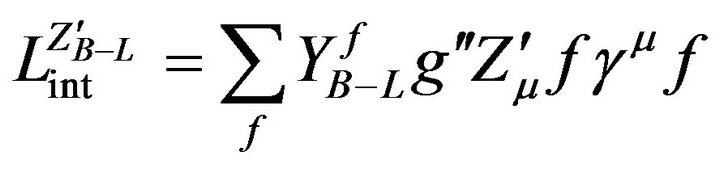 (2)
(2)
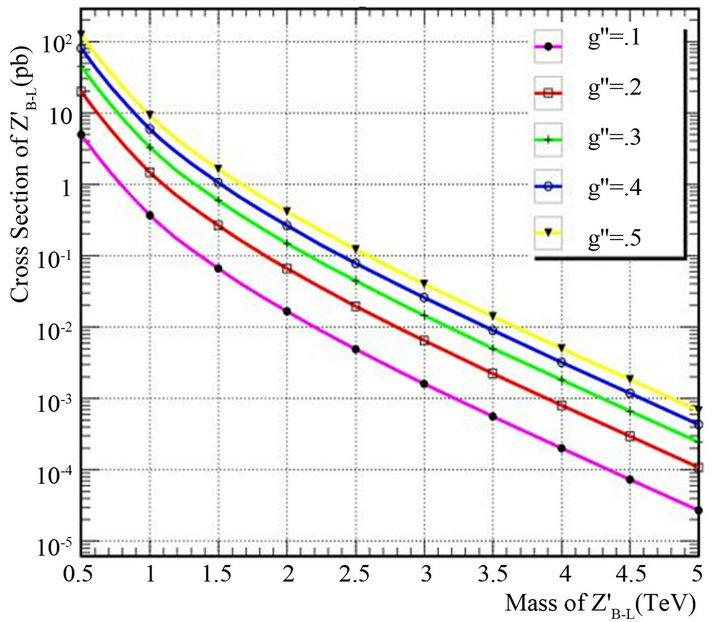
Figure 1. Cross section for 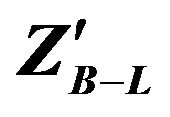 as a function of
as a function of  mass for various
mass for various 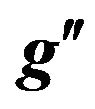 values (where
values (where 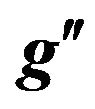 is the U(1)B–L gauge coupling constant) at fixed CM energy of LHC = 14 TeV.
is the U(1)B–L gauge coupling constant) at fixed CM energy of LHC = 14 TeV.

Figure 2. Cross section for  as a function of
as a function of 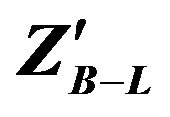 mass for various energies of LHC at √s = 5, 7, 10, 12, 14 TeV at fixed value of
mass for various energies of LHC at √s = 5, 7, 10, 12, 14 TeV at fixed value of .
.
where YB–L is the B-L charge associated with the fermions f (see Table 1). The extra neutral gauge boson 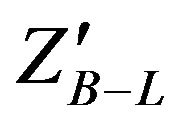 acquires a mass due to the B-L gauge symmetry breaking
acquires a mass due to the B-L gauge symmetry breaking
 (3)
(3)
where  is the U(1)B–L gauge coupling constant and υ′ is the symmetry breaking scale.
is the U(1)B–L gauge coupling constant and υ′ is the symmetry breaking scale.
The production cross sections for 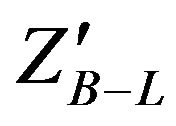 signal in Figures 1 and 2 were computed using MadGraph5 and PYTHIA8 where we generated the process pp → ZB–L of B-L model using MadGraph5 and export this process to PHYTHIA8 then the main switches are on for Initial state Radiation(ISR), Final State Radiation(FSR), FSRinResonances, Decay hadronization, allow resonance decays and master switch for multiparton interactions to stay on.
signal in Figures 1 and 2 were computed using MadGraph5 and PYTHIA8 where we generated the process pp → ZB–L of B-L model using MadGraph5 and export this process to PHYTHIA8 then the main switches are on for Initial state Radiation(ISR), Final State Radiation(FSR), FSRinResonances, Decay hadronization, allow resonance decays and master switch for multiparton interactions to stay on.
2.1.2. Branching Ratios of 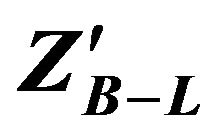
In Figure 3, the branching ratios of 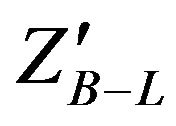 to different quarks are equal approximately and for different leptons are higher than those for quarks. Also the branching ratio for heavy neutrino which have mass 200 GeV in our search is less than those for the charged leptons and light neutrinos. In particular,
to different quarks are equal approximately and for different leptons are higher than those for quarks. Also the branching ratio for heavy neutrino which have mass 200 GeV in our search is less than those for the charged leptons and light neutrinos. In particular,  varies between 17% to 17.5% where (l = electron, muon, tau) but for heavy neutrino
varies between 17% to 17.5% where (l = electron, muon, tau) but for heavy neutrino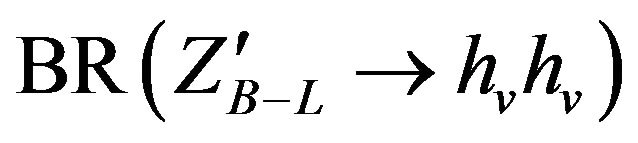 ) varies from 6% to 8% and for light neutrino
) varies from 6% to 8% and for light neutrino  varies between 8.5% to 9% and
varies between 8.5% to 9% and 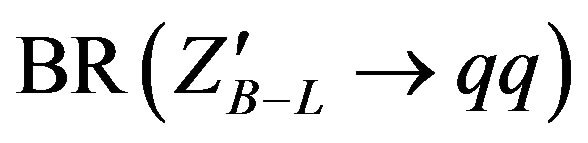 varies from
varies from

Table 1. B-L quantum number for different particles.
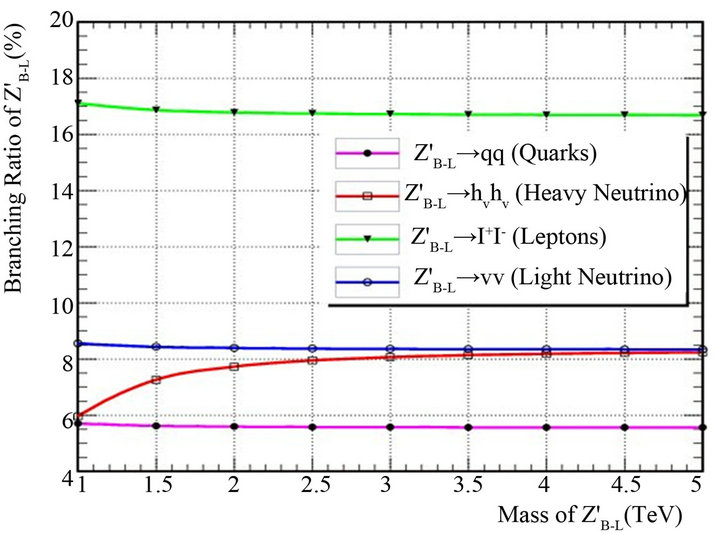
Figure 3. Branching ratios for 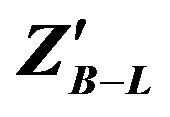 as a function of
as a function of  for
for .
.
5.5% to 6%. The probabilities that  can decay into one light and one heavy neutrino are highly suppressed by the corresponding (heavy-light) neutrino mixing and thus they can safely be neglected. Heavy neutrino is the most characteristic for B-L model so it has an effect on different branching ratios because it is rather massive than the SM neutrino. From Figure 3 one can search for
can decay into one light and one heavy neutrino are highly suppressed by the corresponding (heavy-light) neutrino mixing and thus they can safely be neglected. Heavy neutrino is the most characteristic for B-L model so it has an effect on different branching ratios because it is rather massive than the SM neutrino. From Figure 3 one can search for  at LHC via a clean dilepton signal which can be one of the first new physics signatures to be observed at the LHC. We will study
at LHC via a clean dilepton signal which can be one of the first new physics signatures to be observed at the LHC. We will study 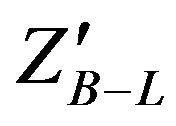 in this paper by using the decay channel of
in this paper by using the decay channel of  to electrons pair using PYTHIA8 and turn off all other decay channels for
to electrons pair using PYTHIA8 and turn off all other decay channels for 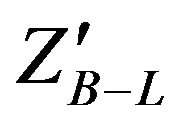 where the ratio of dielctron channel is the highest one.
where the ratio of dielctron channel is the highest one.
2.1.3. Total Width of 
 boson decays only to fermions at tree-level and its width is given by the following expression
boson decays only to fermions at tree-level and its width is given by the following expression
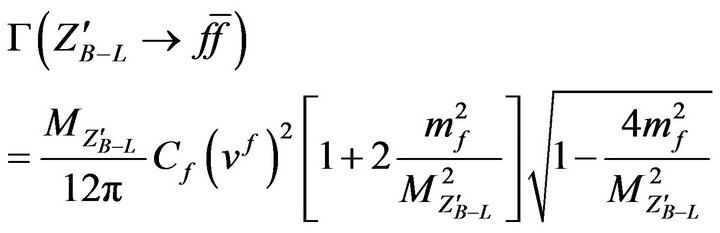 (4)
(4)
where mf is the mass and Cf the number of colors for the fermion type f. In Figure 4 we present the total decay width of the  as a function of
as a function of  mass for fixed values of
mass for fixed values of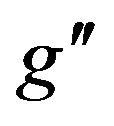 . Figure 5 presents the total decay width of the
. Figure 5 presents the total decay width of the  as a function of
as a function of  for fixed values of
for fixed values of 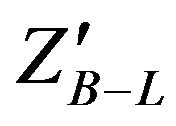 mass.
mass.
From Figures 4 and 5 we note that the total width of a  gauge boson varies from a few hundreds of GeV over a mass range of
gauge boson varies from a few hundreds of GeV over a mass range of  depending on the value of
depending on the value of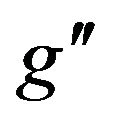 . The decay widths of
. The decay widths of  in this model are then given by:
in this model are then given by:
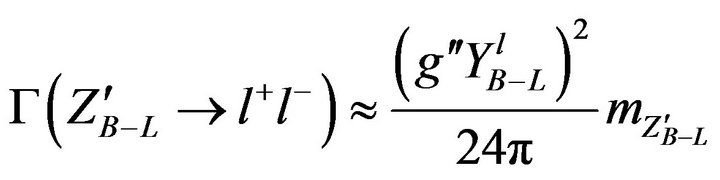 (5)
(5)

Figure 4. Total width for 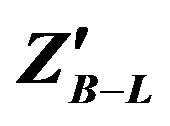 as a function of mass
as a function of mass 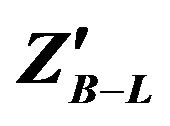 for fixed values of
for fixed values of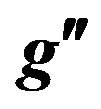 .
.

Figure 5. Total width for  as a function of
as a function of  for fixed values of
for fixed values of 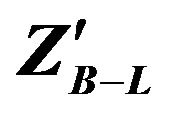 mass.
mass.

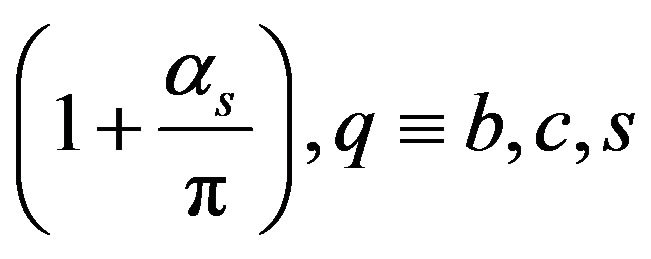 (6)
(6)

 (7)
(7)
The main switches for Initial State Radiation, Final Sate Radiation and multiple interactions are on. Figure 4 presents the total width for  as a function of mass
as a function of mass 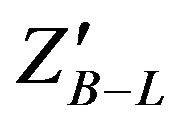 for fixed values of
for fixed values of 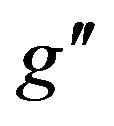 .Here, we used CM energy of LHC 14 MeV. Figure 5 presents the total width for
.Here, we used CM energy of LHC 14 MeV. Figure 5 presents the total width for  as a function of
as a function of 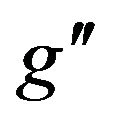 for fixed values of
for fixed values of  mass. We note that the total width of
mass. We note that the total width of 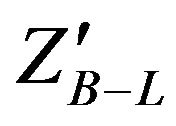 increase with increasing the mass of
increase with increasing the mass of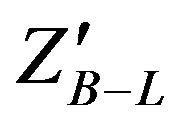 .
.
In Figure 6 we present the relative variation of the total width as a function of the heavy neutrino mass for different values of 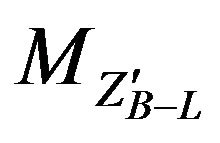 and for
and for . We note the importance of taking into consideration the heavy neutrino since their relative contribution to the total width can be as large as 20% where
. We note the importance of taking into consideration the heavy neutrino since their relative contribution to the total width can be as large as 20% where 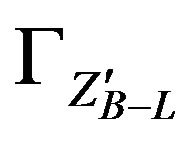 is the total width of
is the total width of  which includes all decay channels (also decay channel of heavy neutrino ) whereas
which includes all decay channels (also decay channel of heavy neutrino ) whereas 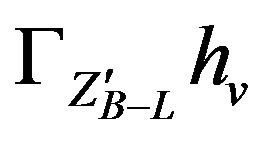 decoupled includes all decay channels except decay channel of heavy neutrino is turn off.
decoupled includes all decay channels except decay channel of heavy neutrino is turn off.
2.2. Detection of 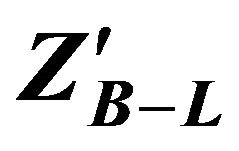 Signal at LHC
Signal at LHC
2.2.1. Dielectron Angular Distribution
In addition to the dilepton invariant mass 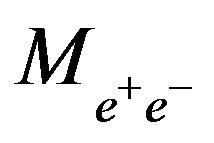 analysis, it has been shown that the angular distribution of the dilepton events [10] can also be used to test the presence of a
analysis, it has been shown that the angular distribution of the dilepton events [10] can also be used to test the presence of a  boson by detecting its interference with the SM Z boson. The massive resonance search technique
boson by detecting its interference with the SM Z boson. The massive resonance search technique
(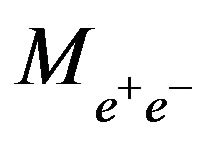 analysis) is extended to include dilepton angular information to detect
analysis) is extended to include dilepton angular information to detect , so we will use the dielectron angular distribution cos(θ*) where θ* is the angle in the dielectron rest reference frame between the negative electron and the incident incoming quark. PYTHIA8 gives θ only in Lab frame but we use θ* here which is in rest frame so we must convert from lab frame to rest frame to get θ* by using boost vector. We define two additional reference frames: a) the colliding proton CM frame denoted by O (this frame is identical to the laboratory frame) and b) The rest frame of the dilepton system denoted by O*. The dilepton system is boosted along the beam axis. The z-axis is chosen as the direction of one of the beams, and it is then identical for O and O* frames. It should be noted that there is a sign ambiguity in the measurement of cos(θ*) since for a particular event, there is no information about whether the incoming quark comes from the positive or negative z directions [11]. Instead, it is useful to consider the quantity
, so we will use the dielectron angular distribution cos(θ*) where θ* is the angle in the dielectron rest reference frame between the negative electron and the incident incoming quark. PYTHIA8 gives θ only in Lab frame but we use θ* here which is in rest frame so we must convert from lab frame to rest frame to get θ* by using boost vector. We define two additional reference frames: a) the colliding proton CM frame denoted by O (this frame is identical to the laboratory frame) and b) The rest frame of the dilepton system denoted by O*. The dilepton system is boosted along the beam axis. The z-axis is chosen as the direction of one of the beams, and it is then identical for O and O* frames. It should be noted that there is a sign ambiguity in the measurement of cos(θ*) since for a particular event, there is no information about whether the incoming quark comes from the positive or negative z directions [11]. Instead, it is useful to consider the quantity , where
, where  is the angle between the dilepton system boost
is the angle between the dilepton system boost  (relative to the O frame) and the lepton direction
(relative to the O frame) and the lepton direction
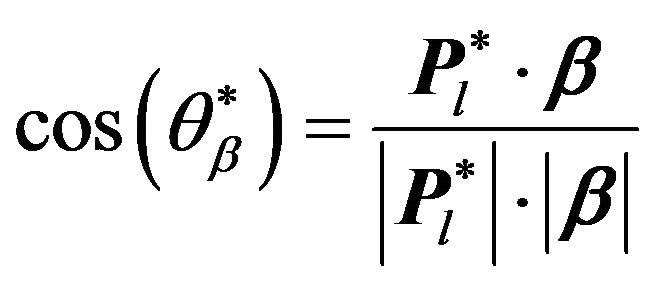 (8)
(8)
where the boost vector is
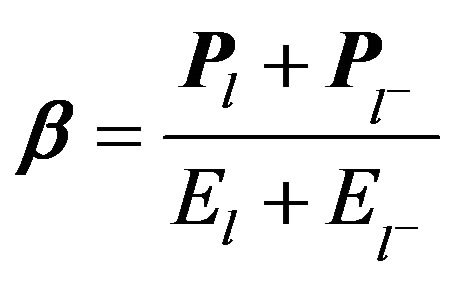 (9)
(9)
In order to obtain 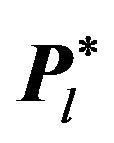 the boost vector of the dilepton system should be found and the transformation to the O* frame should be performed. Figure 7 gives the angular
the boost vector of the dilepton system should be found and the transformation to the O* frame should be performed. Figure 7 gives the angular
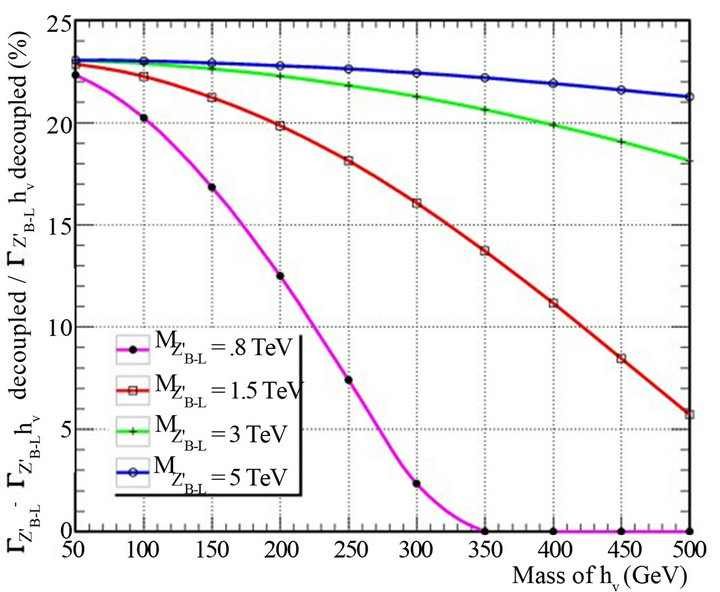
Figure 6. Total width for  as a function of heavy neutrino mass for fixed values of
as a function of heavy neutrino mass for fixed values of 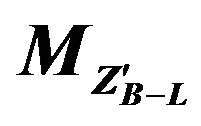 and
and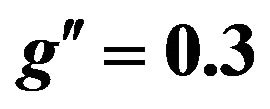 .
.

Figure 7. Angular distribution of dielectron of  boson decay where forward electrons have cos(θ*) > 0 and backward electrons have cos(θ*) < 0.
boson decay where forward electrons have cos(θ*) > 0 and backward electrons have cos(θ*) < 0.
distribution of dielectron of  boson decay as a function of cos(θ*) .
boson decay as a function of cos(θ*) .
2.2.2. Dielectron Asymmetry AFB
In the process  where
where  boson has both vector and axial vector couplings to the fermions, these couplings create an asymmetry in the momentum of the electron visible in the polar angle of the lepton pair's center of mass frame. This polar angle which is measured in the center of mass frame of the leptons is typically referred to as the Collins Soper frame. The angular cross section measured in this frame is given by:
boson has both vector and axial vector couplings to the fermions, these couplings create an asymmetry in the momentum of the electron visible in the polar angle of the lepton pair's center of mass frame. This polar angle which is measured in the center of mass frame of the leptons is typically referred to as the Collins Soper frame. The angular cross section measured in this frame is given by:
 (10)
(10)
Here θ* is the emission angle of the electron relative to the quark momentum in the lepton’s center of mass frame (see Figure 8). The constants A and B are determined by the weak isospin and charge of the incident quarks as well as the mass of the dilepton pair. From this cross section, it is convenient to define Nf as the number of events whose θ* is positive, and Nb as the number of events whose θ* is negative. The asymmetry can then be written as:
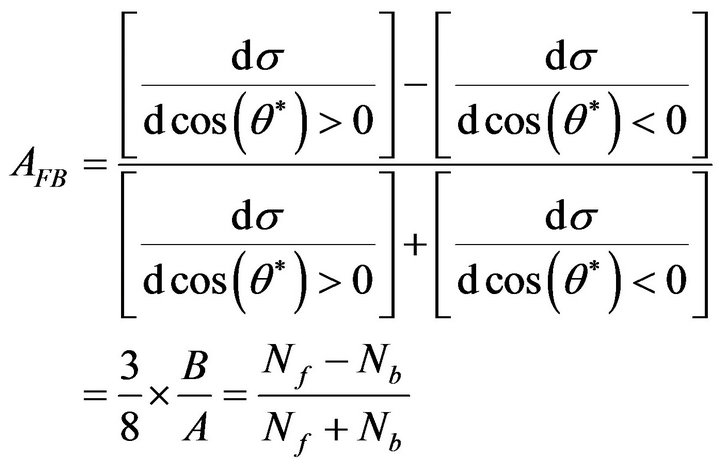 (11)
(11)
This is the general form of the asymmetry.
Collins and Soper noted that an ambiguity exists in the determination of the emission angle θ* when considering
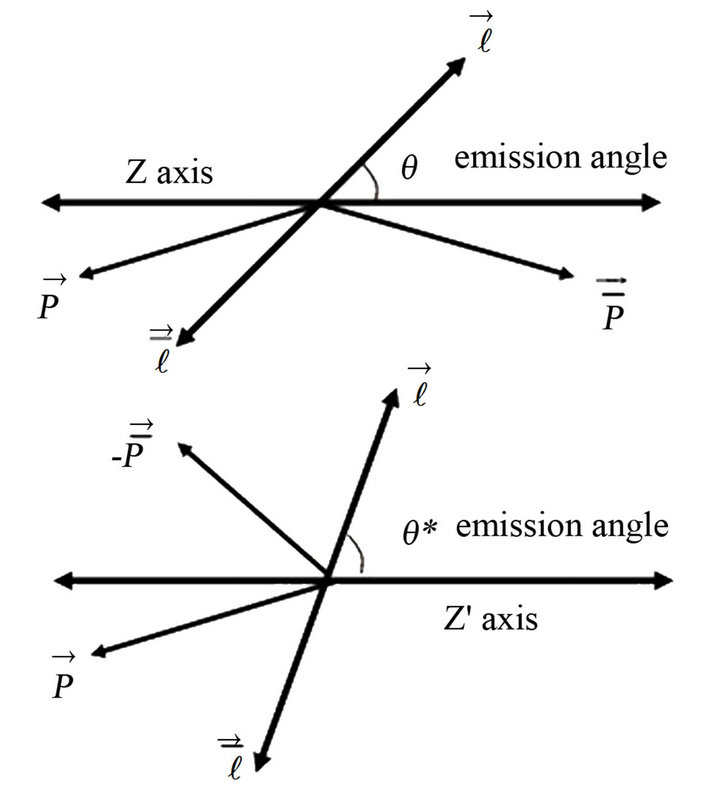
Figure 8. The lepton’s center of mass frame and the CollinsSoper frame.

This Drell-Yan process is quite simple [12] when the incoming quarks have no transverse momentum. In such a case, the emission angle is determined by the angle the electron makes with the proton beam and thus the incoming quark momentum vector. However, since circular acceleration implies a certain amount of transverse momentum by construction, an ambiguity arises. Since the quark’s individual momenta cannot be measured, the momenta boosted into the center of mass frame of the leptons are even more difficult to separate. Consequently, the dependence of the transverse momentum must be minimized. The polar θ* axis is the bisector of the proton beam momentum and the negative (−) of the antiproton beam momentum when the two are boosted into the center of mass frame of the leptons. In so doing, the dependence on the transverse momentum of the incoming quark pair is minimized.
Table 2 shows the numbers of forward and backward electrons produced from  decay in the range of
decay in the range of 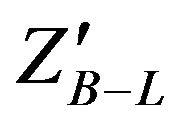 mass 500 GeV to 1500 GeV and also asymmetry calculation.
mass 500 GeV to 1500 GeV and also asymmetry calculation.
Figure 9 shows the dielectron asymmetry distribution for forward and backward electrons for various values of 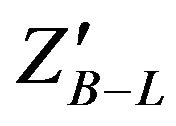 masses.
masses.
2.2.3. Drell Yan Background Events
The histogram in Figure 10 shows the generated dielctron events for a reconstructed mass of 50 to 700 GeV for SM Zo. There is a peak centered on the 100 GeV for 6000 events were generated by PHYTHIA8. This peak, or resonant signal corresponds to the production of a Zo with a mass of 91.188 GeV. This process is called the Drell-Yan spectrum and dielectron are produced from Zo decay and they act as SM background for 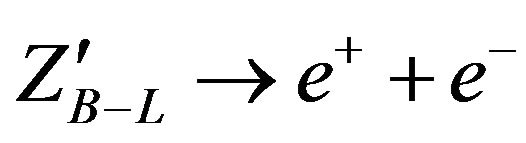 process
process
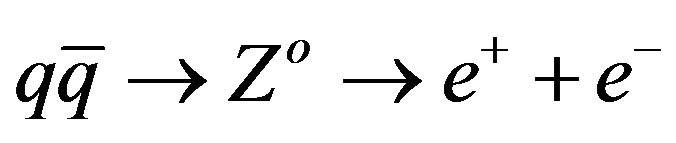
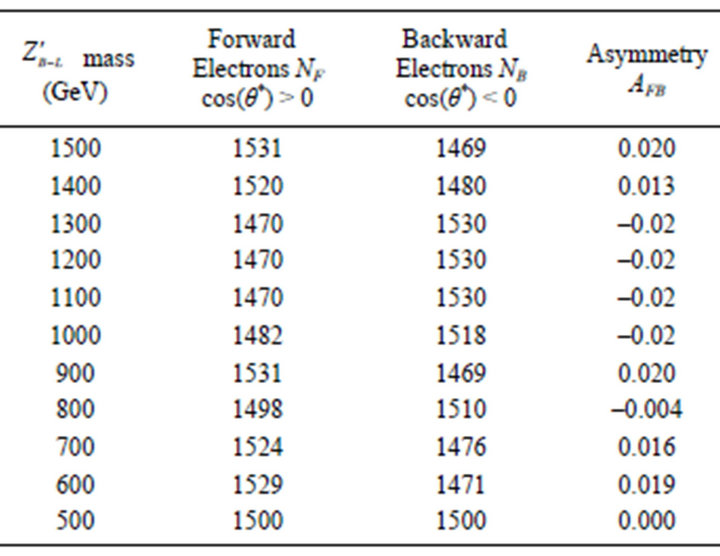
Table 2. The numbers of forward and backward electrons produced from 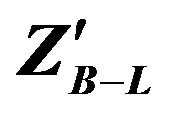 decay in the range of
decay in the range of 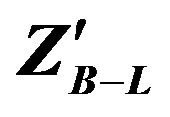 mass 500 GeV to 1500 GeV and also asymmetry calculation.
mass 500 GeV to 1500 GeV and also asymmetry calculation.

Figure 9. Dielectron asymmetry distribution for forward and backward electrons for various values of  masses.
masses.

Figure 10. The Drell-Yan background electrons produced from Zo boson for quark and antiquark annihilation.
Here q is a quark from an incoming proton and it is annihilated with its antiparticle q from another incoming proton and produces a Zo which then decays into two dielectron. The reconstructed mass of Zo will be calculated according to the equation:
 (12)
(12)
2.2.4. Dielectron Invariant Mass
Now, we will use the dilepton invariant mass  from the dilepton events [13] to test the presence of a
from the dilepton events [13] to test the presence of a 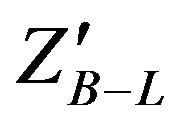 boson at LHC through the massive resonance search technique (
boson at LHC through the massive resonance search technique (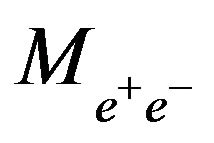 analysis) beside the last method of dilepton angular information to detect
analysis) beside the last method of dilepton angular information to detect 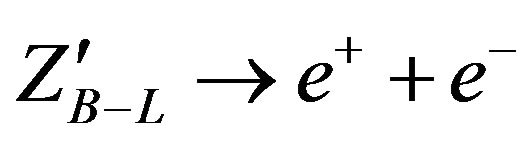 which we have used before. By using PYTHIA8, ROOT and ROOFIT we created a series of
which we have used before. By using PYTHIA8, ROOT and ROOFIT we created a series of 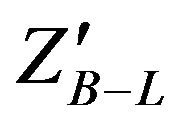 signals with masses from 500 GeV/c2 to 1500 GeV/c2 as in Table 3, then the mass of
signals with masses from 500 GeV/c2 to 1500 GeV/c2 as in Table 3, then the mass of  is reconstructed from the energy and momenta of the selected dielectron at coupling constant equal
is reconstructed from the energy and momenta of the selected dielectron at coupling constant equal 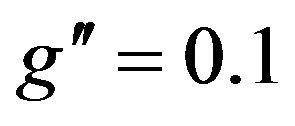 [14]. We generated 5000 events for every signal mass where the backgrounds Drell-Yan events and desired signal events are selected by applying a number of selection cuts on all events samples (5000 events).
[14]. We generated 5000 events for every signal mass where the backgrounds Drell-Yan events and desired signal events are selected by applying a number of selection cuts on all events samples (5000 events).
1) Transverse energy of selected electrons ET > 100 GeV.
2) The selected electrons must be in the central or in the forward regions of |η| < 1.442 or 1.566 < |η| < 2.5 then we choose the two highest-energy electrons where η is the pseudo rapidity of emitted electrons which describes the angle of a particle relative to beam axis.
 (13)
(13)
θ is the angle between the particle momentum vector P and the beam axis (Figure 11).
From Figure 12 we find a peak at 1 TeV which is the reconstruction mass of 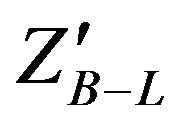 from the electron-positron invariant masses. This allowed us to compare the signal
from the electron-positron invariant masses. This allowed us to compare the signal

Table 3. The expected number of events, signal events for , background events, and Significance calculation at
, background events, and Significance calculation at  using PYTHIA8.
using PYTHIA8.
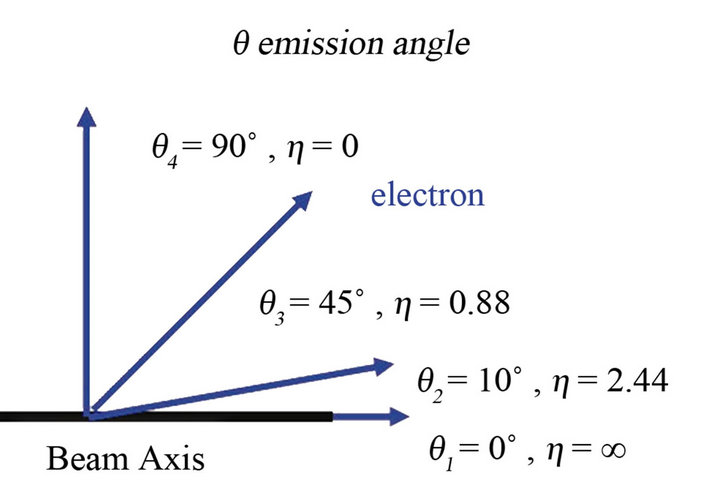
Figure 11. The Pseudo rapidity of produced electrons of 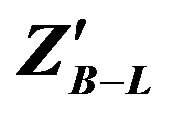 decay.
decay.
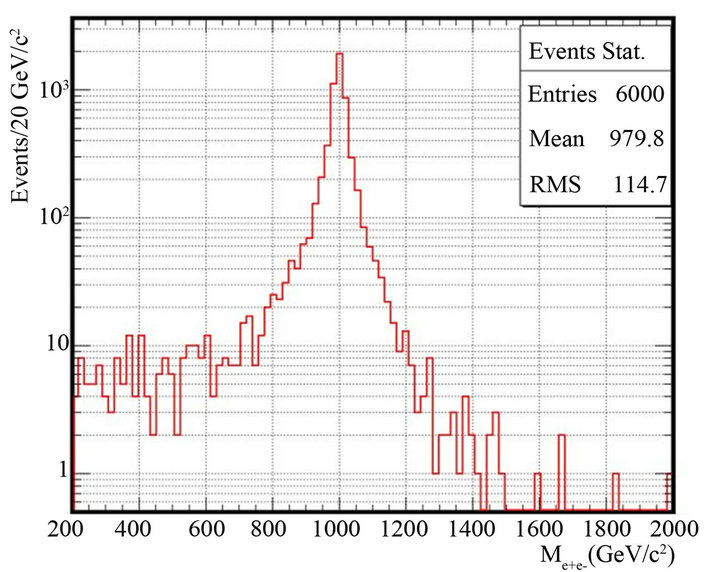
Figure 12. The reconstruction for 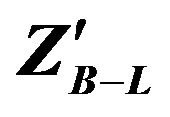 mass from produced dilectron invariant masses at
mass from produced dilectron invariant masses at  mass 1 TeV.
mass 1 TeV.
generated events with the Drell Yan background from Figure 10.
2.3. Properties of 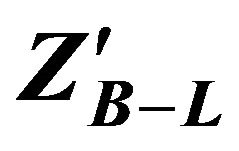
2.3.1. Luminosity
For each generated signal, PYTHIA8 calculated the cross section for each process. This is important because it allows us to scale our generated events to what an actual signal would look like given the luminosity [15]. The luminosity is the number of events collision per unit area in an accelerator. Therefore, the number of expected events Nexp can be determined by the formula: Nexp = Lσ where Nexp = NS + NB and σ is the PYTHIA8 cross section of generated events and L is the luminosity and NS is the number of signal events and NB is the number of background events. Figure 13 give the required luminosity for  observation at LHC for different masses at
observation at LHC for different masses at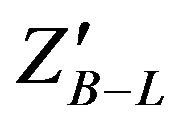 . We note that the value of the luminosity increases by increasing
. We note that the value of the luminosity increases by increasing  mass.
mass.
2.3.2. Significance Calculations
To calculate the significance, each reconstructed mass is fitted by a Gaussian using the ROOFIT package and using the standard deviation with 3σ mass window around the fitted peak for example from Figure 12 at 1000 GeV peak the mass windows is 450 GeV then σ = 75 and µ = 1000. We will integrate the Gaussian from 550 to 1450 to get the fraction of signal event, then we will multiply this fraction by the total expected events Nexp to get the number of signal event NS then we can calculate the background events NB by:
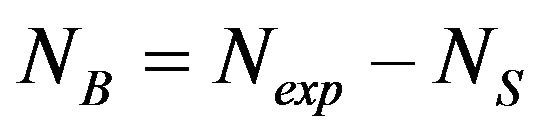 (14)
(14)
The significance formula is:
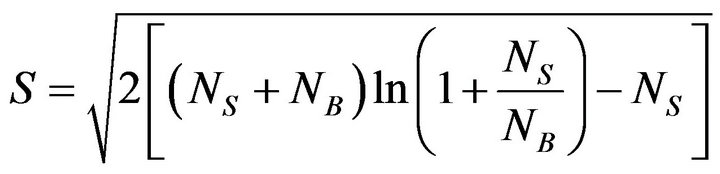 (15)
(15)
where NS is the number of signal events and NB is the number of background events. Table 3 shows a summary of signal events and background events for different values of  mass and the corresponding significance. Figure 14 shows the signal significance as a function of the mass of
mass and the corresponding significance. Figure 14 shows the signal significance as a function of the mass of  for
for .
.

Figure 13. Luminosity required for observation  as a function of
as a function of 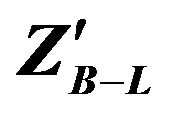 mass for
mass for 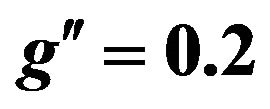 at the CM energy of LHC √s = 14 TeV.
at the CM energy of LHC √s = 14 TeV.

Figure 14. Signal significance as a function of the mass for 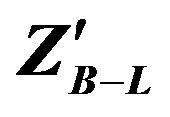 for
for .
.
2.3.3. Transverse Momentum
Figure 15 show the transverse momentum PT distributions of positron and electron pairs in invariant mass region  produced from
produced from  decay. The results are obtained using PYTHIA8 of proton-proton collisions at a center-of-mass energy of 14 TeV at LHC and
decay. The results are obtained using PYTHIA8 of proton-proton collisions at a center-of-mass energy of 14 TeV at LHC and . The distributions are measured over the ranges |η| < 1.442 or 1.566 < |η| < 2.5 and the transverse energy of selected electrons is ET > 100 GeV. The distributions for y and PT are normalized by total cross sections within acceptance regions described are shown in Figures 16 and 17.
. The distributions are measured over the ranges |η| < 1.442 or 1.566 < |η| < 2.5 and the transverse energy of selected electrons is ET > 100 GeV. The distributions for y and PT are normalized by total cross sections within acceptance regions described are shown in Figures 16 and 17.
Figures 18 and 19 show the measurement of the rapidity y where the transverse-momentum PT distributions and rapidity of the  boson provide a new information about the dynamics of proton collisions at high energies and the PT spectrum provides a better understand-
boson provide a new information about the dynamics of proton collisions at high energies and the PT spectrum provides a better understand-

Figure 15. Transverse momentum for dielectron for mass of 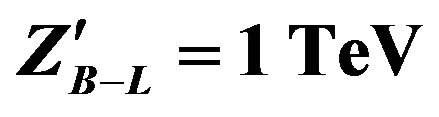 and energy of LHC = 14 TeV and
and energy of LHC = 14 TeV and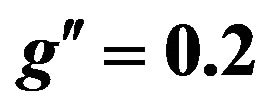 .
.
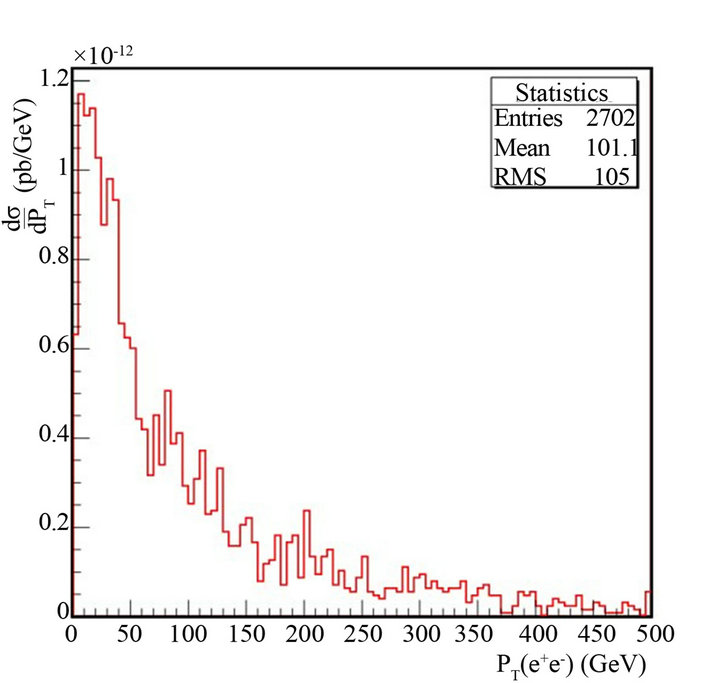
Figure 16. Differential cross section as a function of dielctron transverse momentum at 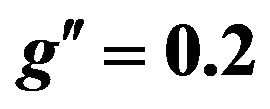 and energy of LHC = 14 TeV.
and energy of LHC = 14 TeV.

Figure 17. The normalized differential cross section for  boson as a function of transverse-momentum of dielectron.
boson as a function of transverse-momentum of dielectron.
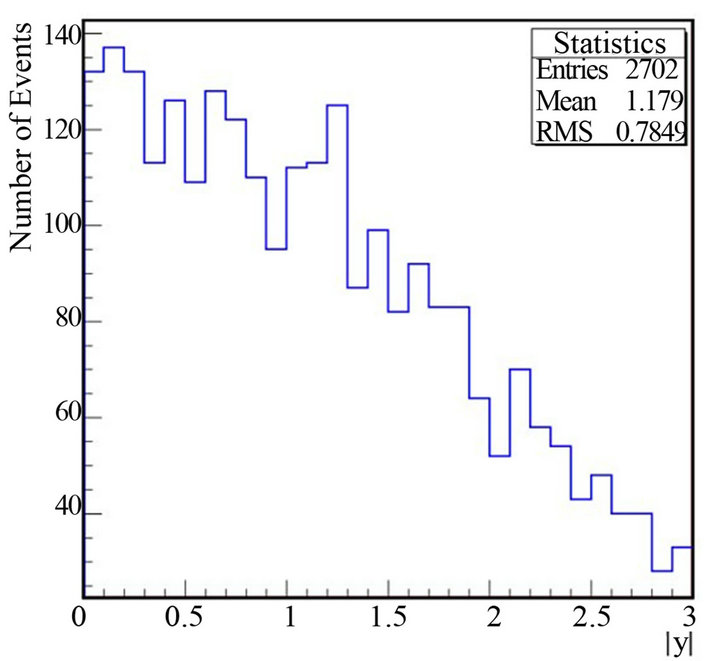
Figure 18. Absolute value of rapidity for dielectron for mass of  and energy of LHC=14 TeV and
and energy of LHC=14 TeV and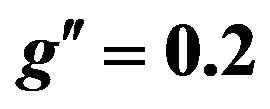 .
.

Figure 19. The normalized differential cross section for  as a function of the absolute value of rapidity of dielectron for mass of
as a function of the absolute value of rapidity of dielectron for mass of 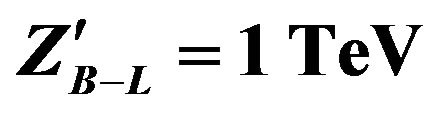 at CM energy of LHC = 14 TeV and
at CM energy of LHC = 14 TeV and .
.
ing of the underlying collision process at low transverse momentum.
The measurements of the rapidity and transverse momentum spectra are based on samples over boson events reconstructed in each dilepton decay mode and collected using high PT single lepton. For the  boson candidates selected pairs of leptons are required to have a reconstructed invariant mass in the range
boson candidates selected pairs of leptons are required to have a reconstructed invariant mass in the range  . The two electrons candidates with the highest PT in the event are used to reconstruct a
. The two electrons candidates with the highest PT in the event are used to reconstruct a  candidate. Electrons are required to have ET >100 GeV and |η| < 1.442 or 1.566 < |η| < 2.5.
candidate. Electrons are required to have ET >100 GeV and |η| < 1.442 or 1.566 < |η| < 2.5.
2.3.4. Rapidity of Z′B.L
The rapidity is defined as
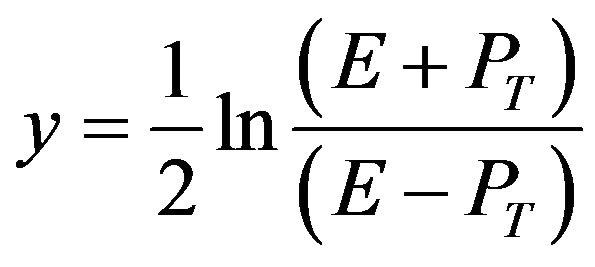 (16)
(16)
where E is the energy of the  candidate and PT is its longitudinal momentum along the anticlockwise beam axis (the z axis of the detector). The y and PT of
candidate and PT is its longitudinal momentum along the anticlockwise beam axis (the z axis of the detector). The y and PT of 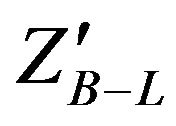 are determined from the leptons momenta. The measured differential dielectron cross sections are normalized to the inclusive Z cross section. The differential cross section is determined in each y or bin by subtracting from the number of detected events in a bin the estimated number of background events. The distributions are corrected for signal acceptance and efficiency and for the effects of detector resolution and electromagnetic finalstate radiation (FSR) using an unfolding technique based on the inversion of a response matrix. The final result takes into account the bin width and is normalized by the measured total cross section.
are determined from the leptons momenta. The measured differential dielectron cross sections are normalized to the inclusive Z cross section. The differential cross section is determined in each y or bin by subtracting from the number of detected events in a bin the estimated number of background events. The distributions are corrected for signal acceptance and efficiency and for the effects of detector resolution and electromagnetic finalstate radiation (FSR) using an unfolding technique based on the inversion of a response matrix. The final result takes into account the bin width and is normalized by the measured total cross section.
The distribution of  bosons is symmetric about y = 0 and therefore the appropriate measurement is the distribution as a function of the absolute value of rapidity The measurement is normalized to the total cross sectio
bosons is symmetric about y = 0 and therefore the appropriate measurement is the distribution as a function of the absolute value of rapidity The measurement is normalized to the total cross sectio
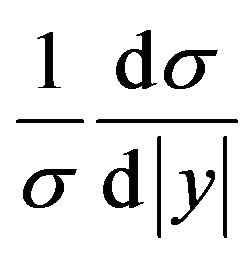 (17)
(17)
and σ is the total cross section is determined by 2702 events
3. Conclusion
In this work, we have presented the LHC potential to discover a heavy neutral massive gauge boson  in B-L extension of SM model via search for two high energy electrons using MC programs where we have simulated the production of
in B-L extension of SM model via search for two high energy electrons using MC programs where we have simulated the production of 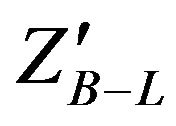 for different center of mass energies at LHC for various values of coupling constant
for different center of mass energies at LHC for various values of coupling constant 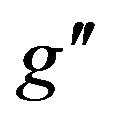 and also presented all possible branching ratios of
and also presented all possible branching ratios of 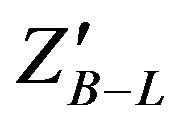 to different decay channels to fermions and presented the total width of
to different decay channels to fermions and presented the total width of . We have used the two high energy electrons angular distribution and the two high energy electrons invariant mass to detect
. We have used the two high energy electrons angular distribution and the two high energy electrons invariant mass to detect  signal at LHC. Finally, we calculated the luminosity, significance, dielectron transverse momentum, rapidity and differential cross section. All these signatures predict the existence of a new gauge boson
signal at LHC. Finally, we calculated the luminosity, significance, dielectron transverse momentum, rapidity and differential cross section. All these signatures predict the existence of a new gauge boson 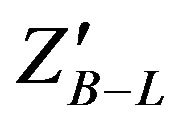 at LHC in the mass range 1 TeV to 1.5 TeV via detection of the two high energy electrons in CMS.
at LHC in the mass range 1 TeV to 1.5 TeV via detection of the two high energy electrons in CMS.
4. Acknowledgements
It is a pleasure to thank L. Basso (Freiburg Univ. Germany) for useful discussions of B-L model, T. Sjostrand (Lund Univ. Sweden) for useful discussions of PYTHIA, J. Alwall (Stanford Univ. USA) for useful discussions of Mad-Graph5/MadEvent and C. Duhr also many thanks to the administration of the faculty of science Cairo University Egypt particular to Prof. Gamal Abd El Nasir, Prof. Sherief Mourad and Prof. Omar Osman.
REFERENCES
- L. Basso, Ph.D. Thesis, University of Southampton, Southampton, 2011.
- L. Basso, Master’s Thesis, University of Padua, Padova, 2007.
- L. Basso, A. Belyaev and S. Moretti, arXiv:0812.4313v1 [hep-ph] 22 Dec 2008.
- T. Sjostrand, S. Mrenna and P. Skands, “PYTHIA 6.4 Physics and Manual,” Journal of High Energy Physics, Vol. 26, 2006. doi:10.1088/1126-6708/2006/05/026
- T. Sjostrand, CERN-LCGAPP-2005-05 July 2005.
- T. Sjostrand. http://home.thep.lu.se/torbjorn/php8160/welcome.php
- T. Sjostrand, P. Eden and C. Friberg, Phys. Commun., 135, 238.
- T. Sjostrand, et al., “High-Energy-Physics Event Generation with Pythia 6.1,” Computer Physics Communications, Vol. 135, No. 2, 2001, pp. 238-259. doi:10.1016/S0010-4655(00)00236-8
- P Mine, Emam 2008 J. Phys. G: Nucl. Part. Phys. 35 115008.
- CDF, Collaboration-arXiv:hep-ex/0602045v1, 2006.
- G. Bella, E. Etzion and N. Hod, “Introduction to the MCnetMOSES Project and Heavy Gauge Bosons Search at the LHC,” arXiv:1004.1649v1 [hep-ex], 2010. http://arxiv.org/pdf/1004.1649.pdf
- D. Bandurin, CMS AN-2008/044, Kansas State University, Manhattan, 2008.
- D. Evans, C. Hill, J. Jackson and D. Newbold, CMS AN-2008/048.
- M. Carena and A. Daleo, arXiv:hep-ph/0408098v1, 2004.
- Christopher Rogan Fall 2004 Junior Paper.

