Open Journal of Microphysics
Vol.2 No.3(2012), Article ID:21694,3 pages DOI:10.4236/ojm.2012.23006
Second Thoughts about the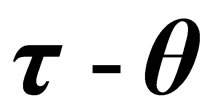 
Puzzle
Grande_Maison_Hosoyama 110, 5-25-7 Hosoyama, Asao-ku, Kawasaki-shi, Kanagawa 215-0001, Japan
Email: kozoaoki@gmail.com
Received April 24, 2012; revised June 3, 2012; accepted June 28, 2012
Keywords: Conservation of Parity; Parity of Pion; Parity of Pentaquark Proton; Parity of Deuteron;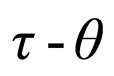 
Puzzle; Conservation of Particle Number
ABSTRACT
The new parity value of 
was determined according to the hypothesis of conservation of particle number. The theoretical pentaquark proton’s parity value was also determined, and it was found that the conservation of parity is account nicely for the 
puzzle.
1. Introduction
In 1951, Panofsky et al. [1] reported on the parities of pions from the reaction of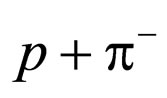 
and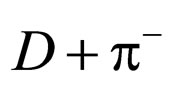
. The reaction between proton (p) and charged pion (
) is
In the general two-body system, the parity formula is
where Pa and Pb are the intrinsic parities, l is the angular momentum. The traditional proton, neutron, and meson’s parity values in common use are +1, +1, and –1, respectively. The parity is a multiplicative quantum number. Since the initial state (
) is S state (l = 0) and the angular momentum is 0, the initial state’s parity is
The final state’s parity is
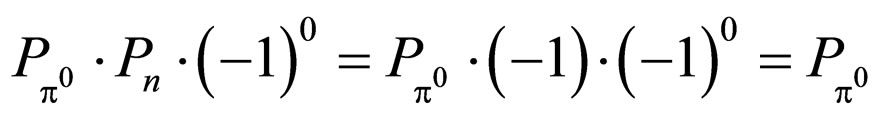
It was considered that the two parities are same by the conservation of parity.
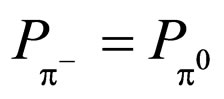
In 1954, Chinowsky and Steinberger [2] obtained the parity value (–1) of 
from the absorption of negative pions in deuterium. In 1959, Plano et al. [3] determined the parity value (–1) of neutral pion (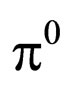
). However the quark numbers by the traditional formula are not add up between the initial state and the final state. It is thought of as a serious problem.
By the way, the two different decays were found for the positively charged strange mesons [3]:
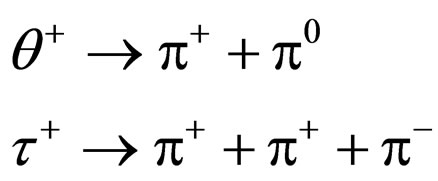
The charged kaon (K+) [4] used to be called 
and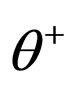
. Both the 
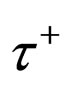and 
particles were supposed to be two different particles, but they are the same particles. The two final states have different parities, and it is known as the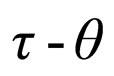 
puzzle [5-8].
In this paper, the parities of the pentaquark proton, deuteron, and neutral pion are re-searched based on the hypothesis of conservation of particle number [9]. It is attested to the conservation of parity for the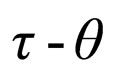 
puzzle.
2. Results and Discussion
2.1. The Parity of 
for the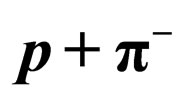 
Reaction
The traditional formula and quark contents by experiment [1,3] are
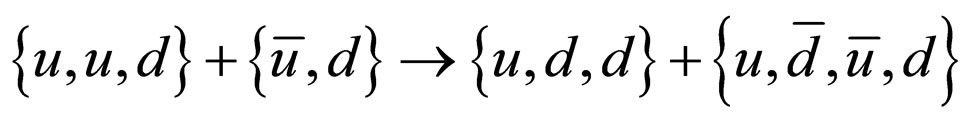
The numbers of down and anti-down quarks, d and d-bar, are not add up between the left-hand member and the right-hand member. It is necessary for the adjustment of particle numbers. To adjust their member, the pentaquark proton (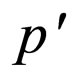
) is adopted [9]. According to the hypothesis of conservation of particle number, the above formulae for 
are as indicated below.
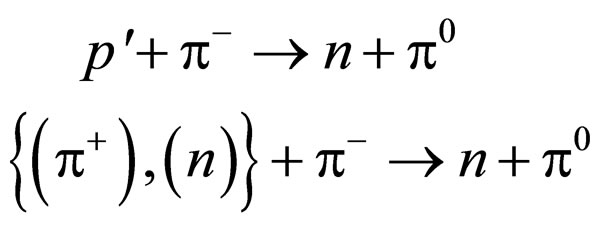
where the {(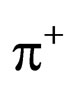
), (n)} is a pentaquark proton (
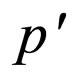), the quark content is {u, d-bar} {u, d, d} [9]. The pentaquark proton’s parity (
) is –1, since the parity formula is
The initial state’s parity is
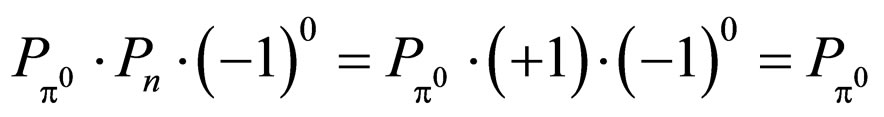
By the conservation of parity,
The new parity value of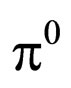 
is +1, not –1 in common use.
2.2. The Parity of 
for the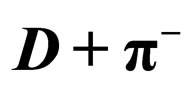 
Reaction
The numbers of down and anti-down quarks are not add up between the left-hand member and the right-hand member by experiment [1].
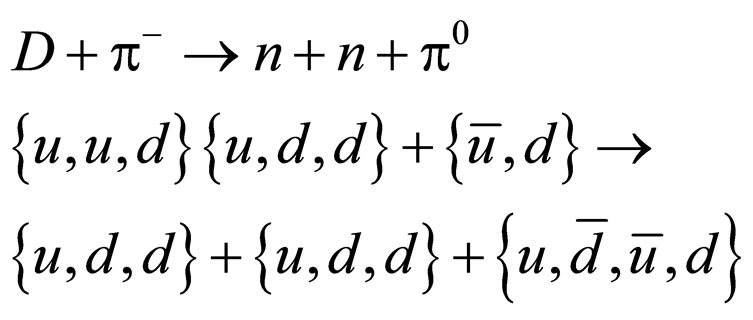
It is necessary for the adjustment of particle numbers. To adjust their member, the pentaquark proton (
) is adopted [9]. According to the hypothesis of conservation of particle number, the above formulae for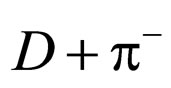 
are as indicated below. The reaction between the deuteron (
) and charged pion (
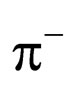) is
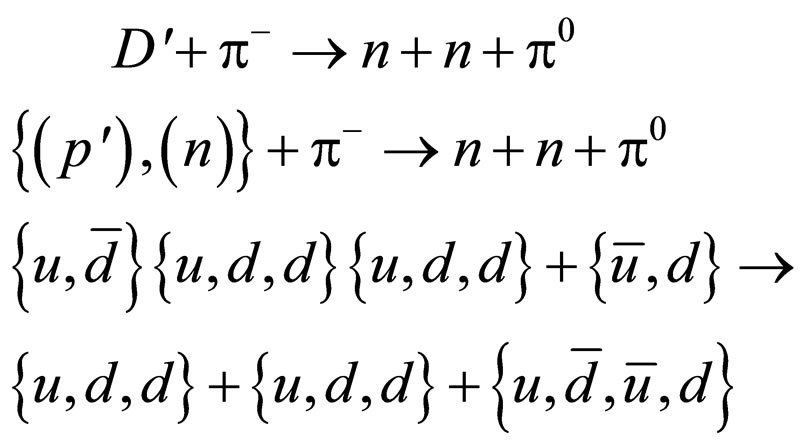
where the {(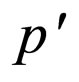
),(n)} is the deuteron(D′) [9].
The deuteron’s parity (PD′) is –1, since the parity formula is
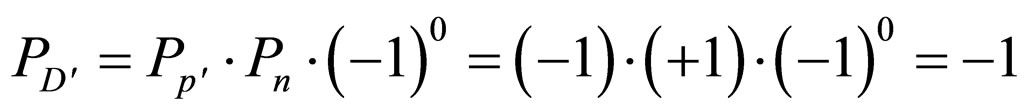
The initial state’s parity is
The final state’s parity is
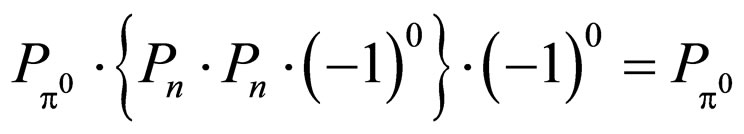
By the conservation of parity,
The new parity value of 
in this reaction is also +1.
2.3. The Parity of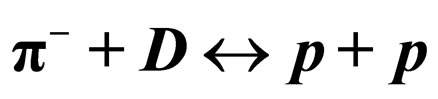 
Reaction
The reaction between the 
and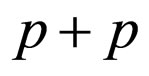 
by experiment [10] is
This reaction was not considered by Aoki [9]. The formula for the quark content
of the traditional proton is
However the numbers of down and anti-down quarks are not add up between the left-hand member and the right-hand member. The parity is not conserved. The formula of the left-hand parity is
The formula of the right-hand parity is:
To adjust their member, the pentaquark proton (p′) is adopted [9].
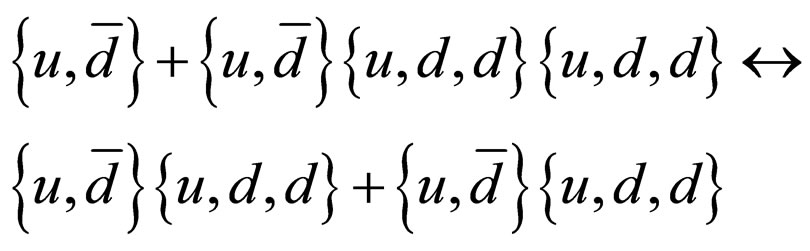
The formula of the left-hand parity is
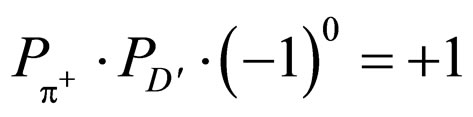
The formula of the right-hand parity is
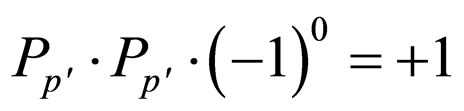
The parity is conserved by the hypothesis of conservation of particle number.
2.4. The Validation of Conservation of Parity for the 
Puzzle
In the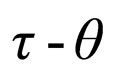 
puzzle [5-8], the two parities of 
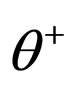and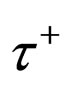 
have same value (–1), since the positively charged Kaon (K+) is a meson. The K+ was shown as follows by Aoki [9].
where the anti-strange quark (s-bar) is the composite particle consisting of the anti-down quark(d-bar) and
, the 
is the 
and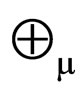 
pair, the 
is the neutrino-antineutrino pair, and the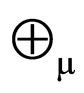 
is the muonneutrino-antimuonneutrino pair. The parity of 
is +1. The 
may be the two photons.
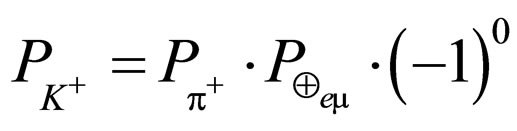
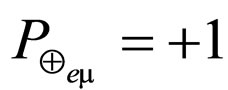
The 
and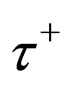 
masses, lifetimes, and spins are no difference with each other. In the traditional expression, the parities are
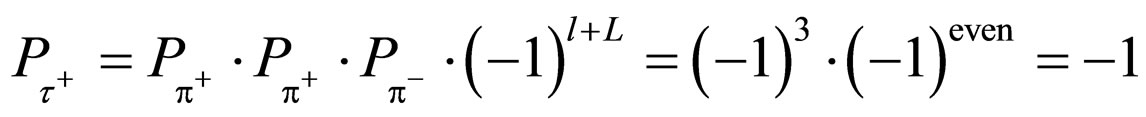
where l is the angular momentum between 
and
, L is the angular momentum between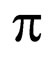 
and the center of
,
.
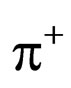The two final states have the different parities, +1 and –1. The parity for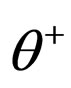 
is not conserved. It is considered as the parity violation in weak interactions. However the parity is conserved as follows by the new parity value (+1) of
.
The neutral pions of both initial states were added by the hypothesis of conservation of particle number. The 
for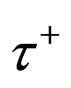 
is corresponding to the
. The initial state’s parities for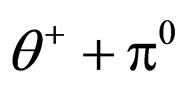 
and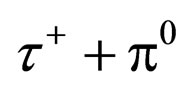 
are –1.
The final state’s parity for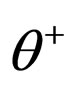 
is –1.
The final state’s parity for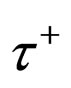 
is –1.
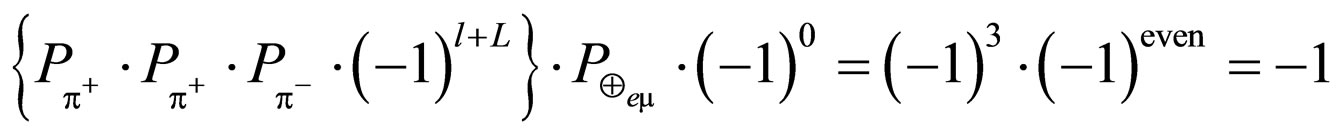
3. Conclusions
The new parity values of the the pentaquark proton (p′)deuteron (D′), and neutral pion (
), are –1, –1, and +1, respectively.
It was attested to the conservation of parity for the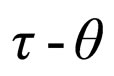 
puzzle.
REFERENCES
- W. K. H. Panofsky, R. L. Aamodt and J. Hadley, “The Gamma-Ray Spectrum Resulting from Capture of Negative π-Mesons in Hydrogen and Deuterium,” Physical Review, Vol. 81, No. 4, 1951, pp. 565-574. doi:10.1103/PhysRev.81.565
- W. Chinowsky and J. Steinberger, “Absorption of Negative Pions in Deuterium: Parity of the Pion,” Physical Review, Vol. 95, No. 6, 1954, pp. 1561-1564. doi:10.1103/PhysRev.95.1561
- R. Plano, A. Prodell, N. Samios, M. Schwartz and J. Steinberger, “Parity of the Neutral Pion,” Physical Review Letters, Vol. 3, No. 11, 1959, pp. 525-527. doi:10.1103/PhysRevLett.3.525
- C. Amsler, et al., “Review of Particle Physics,” Physics Letters B, Vol. 667, No. 1-5, 2008, pp. 1-6. doi:10.1016/j.physletb.2008.07.018
- R. H. Dalitz, “The Decay of the t-Meson,” Proceedings of the Royal Society, Section A, Vol. 66, No. 8, 1953, pp. 710-713.
- R. H. Dalitz, “On the Analysis of t-Meson Data and the Nature of the Meson,” Philosophical Magazine, Vol. 44, No. 357, 1953, pp. 1068-1080.
- R. H. Dalitz, “Decay of t-Mesons of Known Charge,” Physical Review, Vol. 94, No. 4, 1954, pp. 1046-1051. doi:10.1103/PhysRev.94.1046
- A. K. Wróblewski, “The Downfall of Parity: The Revolution That Happened Fifty Years Ago,” Acta Physica Polonica B, Vol. 39, No. 2, 2008, pp. 251-264.
- K. Aoki, “Hypothesis of Conservation of Particle Number,” Open Journal of Microphysics, Vol. 1, No. 1, 2011, pp. 1-12. doi:10.4236/ojm.2011.11001
- R. Durbin, H. Loar and J. Steinberger, “The Spin of the Pion via the Reaction p+ + d «p + p,” Physical Review, Vol. 83, No. 3, 1951, pp. 646-648.