Received 9 September 2015; accepted 3 April 2016; published 6 April 2016

ABSTRACT

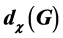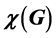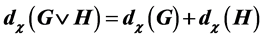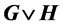We investigate the dominating-c-color number, , of a graph G. That is the maximum number of color classes that are also dominating when G is colored using colors. We show that where is the join of G and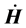. This result allows us to construct classes of graphs such that 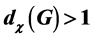and 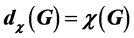thus provide some infor- mation regarding two questions raised in [1] and [2] .

Keywords:

Graph Coloring, Dominating Sets, Dominating Coloring Classes, Chromatic Number, Dominating Color Number

1. Introduction

Let G be a graph with vertex set V and edge set E. A subset I of V is independent if no two vertices in I are adjacent. A subset S of V is a dominating set if every vertex in 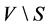is adjacent to at least one vertex in S. We define a coloring C of G with k colors to be a partition of V into k independent sets:

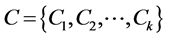
such that

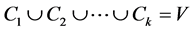
and 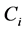is independent for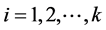. The minimum of k for which such a partition is possible is the chromatic number of G, denoted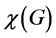. The dominating-c-color number of G is motivated by a two-stage optimization problem. First, we partition the vertex set of G into the minimum number of independent sets; secondly, we maximize the independent sets that are also dominating in G. Clearly, the number of independent sets we use in the first stage will be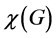, the chromatic number of G. Among all colorings of G using 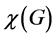colors, the maximum number of independent sets that are also dominating is defined to be the dominating- c-color number of G, denoted by. Formally, we have

The dominating-c-color number of G was first introduced in [2] . More research has been done in this area since then (see for example [1] [3] [4] ). However, the two interesting questions posed in [1] and [2] remain unanswered. In this article, we present some more results about the dominating-c-color number of a graph that are relevant to these two questions.

2. Main Results

The following observation was made in [2] .

Theorem 1 For all graph G,

The following two questions are posed in [1] and [2] .

Question 1. Characterize the graphs G for which

Question 2. Characterize the graphs G for which

Neither of the two extreme cases is trivial. It is known that if G has an isolated vertex, then. However, a graph G with can be connected and have arbitrarily large minimum degree.

Theorem 2. [1] For every integer there exists a connected graph G with and

The following lemma may help us understand the relation between the structure of a graph and its dominating-c-color number. It shows that if a graph G contains a complete bipartite graph as a spanning subgraph, then the dominating-c-color number of G is the sum of the dominating-c-color numbers of these two subgraphs.

Lemma 1. If can be partitioned into two sets and such that every vertex in is adjacent to every vertex in, then where is the subgraph of G induced by for.

Proof. Since in any coloring of G, no vertex in can share a color with a vertex in, we have. Let and. Let be a -coloring of with dominating coloring classes using the colors. Let be a -coloring of with dominating coloring classes using the colors. The combination of and is clearly a -coloring of G. A coloring class of C is either a coloring class of or a coloring class of. Suppose that S is a coloring class of that dominates. Every vertex in is adjacent to at least one vertex in S. Every vertex in is adjacent to every vertex in. Therefore S is a dominating set in G. Similarly, every coloring class of that dominates is a dominating set in G. C is a coloring of G with at least coloring classes. We have

Suppose that is a coloring of G with colors and dominating coloring classes. The restriction of to is a coloring of with colors for. Let S be a dominating coloring class of. or. Suppose that. Then S is a dominating set for. Therefore, every dominating coloring class of is either a dominating coloring class of or a dominating coloring class of. Therefore

Using Lemma 1, we have a sufficient condition for the dominating-c-color number of a graph to be greater than one.

Corollary 1. If the complement of G is disconnected, then.

The join of two graphs and, denoted by, is defined by

In other words, we construct by taking a copy of each of and and joining every vertex in with every vertex in. It is known that By Lemma 1, there is a similar relation between the dominating-c-color numbers.

Theorem 3.

It is shown in [1] that it is possible for a graph with chromatic number k to have dominating-c-color number l for any k such that and. We present a new construction to prove this result using Theorem 3.

Theorem 4. For all integers such that and there exists a connected graph G with and.

Proof. We prove by induction on l. If, the existence of such graphs is guaranteed by Theorem 2. For it is easy to check that and Therefore the theorem is true for. Suppose that and Let and By inductive hypothesis, there is a connected graph H with and. Let Since, by Theorem 3 we have

and

This proves the theorem.

Next we turn our attention to Question 2. Arumugam et al. [2] showed that if G is uniquely c-colorable, then. Therefore if G contains a subgraph that is uniquely -colorable, then. It is natural to ask whether there are any other kind of such graph, that is, whether there are any graph G such that and G does not contain a uniquely k-colorable subgraph. For, the answer is no since every edge is a uniquely 2-colorable subgraph. For, the answer is yes. Arumugam et al. [1] showed that for any nonnegative integer i. was not uniquely 3-colorable for. Using this fact and Theorem 3, we can show that the answer of our question is yes for all.

First, we need a technical lemma.

Lemma 2. The graph is uniquely -colorable if and only if is uniquely -colorable and is uniquely -colorable.

The proof is easy and omitted.

Theorem 5. Let k be an integer greater than 3. There is a graph such that and do not contain a uniquely k-colorable subgraph.

Proof. We prove by induction on k. We have shown that the statement is true for. Suppose that and the statement is true for. Let Since by Theorem 3 and the inductive hypothesis. Every k-chromatic subgraph H of must have the form where is a subgraph of. By Lemma 2, H is uniquely k-colorable if and only if is uniquely -colorable. Since does not contain a uniquely - colorable subgraph, does not contain any uniquely k-colorable subgraph. This proves the theorem.

The graphs constructed in Theorem 5 contain large cliques. In fact, contains many copies of. If for some integers l and j, we may reduce the size of the largest clique in by taking the join of copies of in the first l steps and then taking the join with afterwards. Thus, we have the following result.

Theorem 6. Let be nonnegative integers and. There is a graph such that. does not contain a uniquely k-colorable subgraph and the largest clique in has size.

3. Remarks

It is well known that there are uniquely k-colorable graphs with arbitrarily large girth. Therefore, there are graphs G such that and G has arbitrarily large girth. In light of Theorems 5 and 6, we would like to ask the following question.

Question 3. Are there triangle-free graphs G such that and does G not contain a uniquely k-colorable graph? Furthermore, are there such graphs with arbitrarily large girth?

Cite this paper

Bing Zhou, (2016) On the Maximum Number of Dominating Classes in Graph Coloring. Open Journal of Discrete Mathematics,06,70-73. doi: 10.4236/ojdm.2016.62006

References