Open Journal of Discrete Mathematics
Vol.05 No.03(2015), Article ID:58268,10 pages
10.4236/ojdm.2015.53005
On the Signed Domination Number of the Cartesian Product of Two Directed Cycles
Ramy Shaheen
Department of Mathematics, Faculty of Science, Tishreen University, Lattakia, Syria
Email: shaheenramy2010@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 March 2015; accepted 21 July 2015; published 24 July 2015
ABSTRACT
Let D be a finite simple directed graph with vertex set V(D) and arc set A(D). A function  is called a signed dominating function (SDF) if
is called a signed dominating function (SDF) if 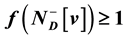 for each vertex
for each vertex . The weight
. The weight 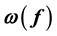 of f is defined by
of f is defined by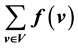 . The signed domination number of a digraph D is
. The signed domination number of a digraph D is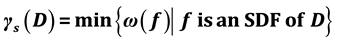 . Let Cm × Cn denotes the cartesian product of directed cycles of length m and n. In this paper, we determine the exact values of gs(Cm × Cn) for m = 8, 9, 10 and arbitrary n. Also, we give the exact value of gs(Cm × Cn) when m,
. Let Cm × Cn denotes the cartesian product of directed cycles of length m and n. In this paper, we determine the exact values of gs(Cm × Cn) for m = 8, 9, 10 and arbitrary n. Also, we give the exact value of gs(Cm × Cn) when m, 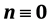 (mod 3) and bounds for otherwise.
(mod 3) and bounds for otherwise.
Keywords:
Directed Graph, Directed Cycle, Cartesian Product, Signed Dominating Function, Signed Domination Number

1. Introduction
Throughout this paper, a digraph 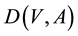 always means a finite directed graph without loops and multiple arcs, where
always means a finite directed graph without loops and multiple arcs, where  is the vertex set and
is the vertex set and 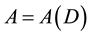 is the arc set. If uv is an arc of D, then say that v is an out-neighbor of u and u is an in-neighbor of v. For a vertex
is the arc set. If uv is an arc of D, then say that v is an out-neighbor of u and u is an in-neighbor of v. For a vertex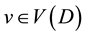 , let
, let 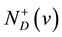 and
and  denote the set of out-neighbors and in-neighbors of v, respectively. We write
denote the set of out-neighbors and in-neighbors of v, respectively. We write 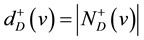 and
and 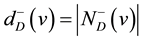 for the out-degree and in-degree of v in D, respectively (shortly
for the out-degree and in-degree of v in D, respectively (shortly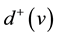 ,
,

















graph D is
The Cartesian product 







In the past few years, several types of domination problems in graphs had been studied [3] -[7] , most of those belonging to the vertex domination. In 1995, Dunbar et al. [3] , had introduced the concept of signed domination number of an undirected graph. Haas and Wexler in [1] , established a sharp lower bound on the signed domination number of a general graph with a given minimum and maximum degree and also of some simple grid graph. Zelinka [8] initiated the study of the signed domination numbers of digraphs. He studied the signed domination number of digraphs for which the in-degrees did not exceed 1, as well as for acyclic tournaments and the circulant tournaments. Karami et al. [9] established lower and upper bounds for the signed domination number of digraphs. Atapour et al. [10] presented some sharp lower bounds on the signed k-domination number of digraphs. Shaheen and Salim in [11] , were studied the signed domination number of two directed cycles Cm ´ Cn when m = 3, 4, 5, 6, 7 and arbitrary n. In this paper, we study the Cartesian product of two directed cycles Cm and Cn for mn ≥ 8n. We mainly determine the exact values of


Theorem 1.1 (Zelinka [8] ). Let D be a directed cycle or path with n vertices. Then
Lemma 1.2 (Zelinka [8] ). Let D be a directed graph with n vertices. Then
Corollary 1.3 (Karami et al. [9] ). Let D be a directed of order n in which 


In [11] , the following results are proved.
Theorem 1.4 [11] :








2. Main Results
In this section we calculate the signed domination number of the Cartesian product of two directed cycles Cm and Cn for m = 8, 9, 10 and 
The vertices of a directed cycle Cn are always denoted by theintegers 




Let us introduce a definition. Suppose that f is a signed dominating function for Cm ´ Cn, and assume that



Remark 2.1: Let f is a 



Since Cm × Cn is 2-regular, it follows from 










Remark 2.2. Since the case 
Let f be a signed dominating function for Cm ´ Cn, then we denote 
column Kj and put

Then we have
For the remainder of this section, let f be a signed domination function of Cm × Cn with signed dominating sequence
Lemma 2.3. If 



Proof. Let








Theorem 2.4.
Proof. We define a signed dominating function f as follows:







By the definition of f, we have sj = 2 for j is odd and sj = 4 for j is even. Notice, f is a SDF for C8 × Cn when

Now, let us define the following functions:


We note:
f1 is a SDF of C8 × Cn when
f2 is a SDF of C8 × Cn when
f3 is a SDF of C8 × Cn when
f4 is a SDF of C8 × Cn when
Hence,

For example, f1 is a SDF of C8 × C12, where
{Here, we must note that, for simplicity of drawing the Cartesian products of two directed cycles Cm × Cn, we do not draw the arcs from vertices in last column to vertices in first column and the arcs from vertices in last row to vertices in first row. Also for each figure of Cm × Cn, we replace it by a corresponding matrix by signs − and + which descriptions −1 and +1 on figure of
By Remark 2.2, for any minimum signed dominating function f of C8 × Cn with signed dominating sequence





Hence, by (1), (2) and (3) we get


Assume that
Let f' ba a signed dominating function with signed dominating sequence
If m, n ≤ 7, then by Theorem 1.4 is the required (because
Claim 2.1. For k ≥ 2, we have 


Figure 1. (a) A signed dominating function of C8 × C12; (b) A corresponding matrix of a signed dominating function of C8 × C12.
Proof of Claim 2.1. We have the subsequence 
Now, if 



Assume that 

Case 1. If 



Case 2. Let


For


Assume that 



For the case 3, we need the following claim:
Claim 2.2. Let f' be a minimum signed dominating function of C8 × Cn with signed dominating sequence

Figure 2. The form
Case 3. Let 

Then we have
Since the case 

If



If



Let 

Then we have one possible is as the form





By Lemma 1.2, and above arguments, we conclude that


Hence, from (1), (15) and (16), deduce that
Finally, we result that:

Theorem 2.5.
Proof. We define a signed dominating function f as follows: 



By define f, we have sj = 3 for





From Corollary 1.3 is


For
If
By Remark 2.2, we have sj = 1, 3, 5, 7 or 9. By Lemma 2.3, if sj = 1 then



cases 


We define
Then we have
Figure 3. A corresponding matrix of a signed dominating function of C9 × C6.
If we have one case from the cases X9 ≥ 1, X7 ≥ 2, X5 + X7 ≥ 2 or X5 ≥ 3. Then by (19) is
Assume the contrary, i.e., (X9 = 0, X7 < 2, X5 + X7 < 2 and X5 < 3).
Hence,
Claim 2.3. There is only one possible for 



The proof comes immediately by the drawing. □
Case 1. X7 = 1 and X5 = X9 = 0. Without loss of generality, we can assume sn = 7. Then we have the form






Subcase 1.1. For






Subcase 1.2. For






Case 2. X5 = 2 and






Subcase 2.1. d = 1, without loss of generality, we can assume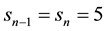
For




Subcase 2.2. d = 2, let

If n º 1(mod 3), then





Subcase 2.3. d = 3, let




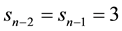





Subcase 2.4. d ≥ 4, let 

We have the form






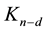









Finally, we deduce that does not exist a signed dominating function f of C9 × Cn for 


From (18) and (20) is
Theorem 2.6.
Proof. We define a signed dominating function f as follows:











and 

By define f and 


is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
is a SDF for C10 × Cn when
For an illustration 



By Remark 2.2, we have sj = 0, 2, 4, 6, 8 or 10. Also by Lemma 2.3, if sj = 0, then 




So, we get
Corollary 2.7. For
Proof. By Corollary 1.3 we have

Let us a signed dominating function f as follows: 








By define f, we have sj = m/3 for




For n º 1, 2(mod 3).
Let 



Thus,


Figure 4. A corresponding matrix of a signed dominating function of C10 × C11.
3. Conclusions
This paper determined that exact value of the signed domination number of Cm × Cn for m = 8, 9, 10 and arbitrary n. By using same technique methods, our hope eventually lead to determination 
Based on the above (Lemma 2.3 and Theorems 1.4, 2.4, 2.5 and 2.6), also by the technique which used in this paper, we again rewritten the following conjecture (This conjecture was mention in [11] ):
Conjecture 3.1.
Cite this paper
RamyShaheen, (2015) On the Signed Domination Number of the Cartesian Product of Two Directed Cycles. Open Journal of Discrete Mathematics,05,54-64. doi: 10.4236/ojdm.2015.53005
References
- 1. Haas, R. and Wexler, T.B. (1999) Bounds on the Signed Domination Number of a Graph. Discrete Mathematics, 195, 295-298.
http://dx.doi.org/10.1016/S0012-365X(98)00189-7 - 2. West, D.B. (2000) Introduction to Graph Theory. Prentice Hall, Inc., Upper Saddle River.
- 3. Dunbar, J.E., Hedetniemi, S.T., Henning, M.A. and Slater, P.J. (1995) Signed Domination in Graphs, Graph Theory, Combinatorics and Application. John Wiley & Sons, Inc., Hoboken, 311-322.
- 4. Cockayne, E.J. and Mynhart, C.M. (1996) On a Generalization of Signed Domination Functions of Graphs. Ars Combinatoria, 43, 235-245.
- 5. Hattingh, J.H. and Ungerer, E. (1998) The Signed and Minus k-Subdomination Numbers of Comets. Discrete Mathematics, 183, 141-152.
http://dx.doi.org/10.1016/S0012-365X(97)00051-4 - 6. Xu, B. (2001) On Signed Edge Domination Numbers of Graphs. Discrete Mathematics, 239, 179-189.
http://dx.doi.org/10.1016/S0012-365X(01)00044-9 - 7. Broere, I., Hattingh, J.H., Henning, M.A. and McRae, A.A. (1995) Majority Domination in Graphs. Discrete Mathematics, 138, 125-135.
http://dx.doi.org/10.1016/0012-365X(94)00194-N - 8. Zelinka, B. (2005) Signed Domination Numbers of Directed Graphs. Czechoslovak Mathematical Journal, 55, 479-482.
http://dx.doi.org/10.1007/s10587-005-0038-5 - 9. Karami, H., Sheikholeslami, S.M. and Khodkar, A. (2009) Lower Bounds on the Signed Domination Numbers of Directed Graphs. Discrete Mathematics, 309, 2567-2570.
http://dx.doi.org/10.1016/j.disc.2008.04.001 - 10. Atapour, M., Sheikholeslami, S., Hajypory, R. and Volkmann, L. (2010) The Signed k-Domination Number of Directed Graphs. Central European Journal of Mathematics, 8, 1048-1057.
http://dx.doi.org/10.2478/s11533-010-0077-5 - 11. Shaheen, R. and Salim, H. (2015) The Signed Domination Number of Cartesian Products of Directed Cycles. Submitted to Utilitas Mathematica.







































