Open Journal of Discrete Mathematics
Vol.4 No.3(2014), Article
ID:47540,10
pages
DOI:10.4236/ojdm.2014.43010
Classification of the Subsets , and the Additive Channals
, and the Additive Channals
Vladimir Leontiev1, Garib Movsisyan2, Arthur Osipyan1
1Moscow State University, Moscow, Russia
2BIT Group, Moscow, Russia
Email: vkleontiev@yandex.ru, garib@firmbit.ru, osipyan.arthur.a@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 April 2014; revised 23 May 2014; accepted 22 June 2014
ABSTRACT
The problem of classification of the subset of the vertices of the n-dimensional unit cube in respect to all “shifts” by a vector from 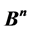 is studied. Some applications for the investigation of the additive channels of communication are represented.
is studied. Some applications for the investigation of the additive channels of communication are represented.
Keywords:Additive Channel, Code, Group, Stabilizer, Cardinality, Transitive Set

Let 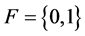 be a two element Galois field and
be a two element Galois field and  be an n-dimensional space on that field. In other words,
be an n-dimensional space on that field. In other words,  is the set of vertices of the n-dimensional unit cube,
is the set of vertices of the n-dimensional unit cube, 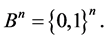 The subsets
The subsets 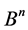 have many different interpretations in the terms of Boolean function theory, or of correcting code theory, or of partially ordered set theory, or that of additive channels etc. And each of these theories is connected with a certain class of restrictions imposed on the properties of the subsets,
have many different interpretations in the terms of Boolean function theory, or of correcting code theory, or of partially ordered set theory, or that of additive channels etc. And each of these theories is connected with a certain class of restrictions imposed on the properties of the subsets,  We consider the “shift” of the subsets
We consider the “shift” of the subsets , and we define equvalence as equality that is accurate within the shift. To define the subsets stabilizers and the transitive subfamilies we use the classic ways connected with Burnside’s Lemma.
, and we define equvalence as equality that is accurate within the shift. To define the subsets stabilizers and the transitive subfamilies we use the classic ways connected with Burnside’s Lemma.
Let 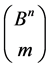 be the family of all m-element subsets of the cube
be the family of all m-element subsets of the cube 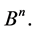 The transformation group
The transformation group  operates on this set as follows. For any
operates on this set as follows. For any 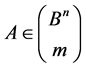 and
and 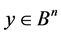 let the following is valid:
let the following is valid:
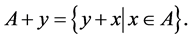
Thus 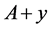 is the shift of the set
is the shift of the set 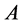 on the vector
on the vector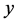 . The transitive set generated by
. The transitive set generated by  has the standard form:
has the standard form:
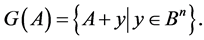
The family 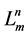 of all transitive sets
of all transitive sets 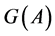 generates the partition
generates the partition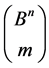 :
:

The cardinality  of a transitive set is found in terms of the stabilizer
of a transitive set is found in terms of the stabilizer 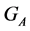 of the set
of the set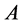 :
:
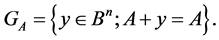
It is well known [1] [2] that  is a subsets in
is a subsets in 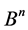 and the cardinality of the transitive set
and the cardinality of the transitive set  is equal to the index of the subsets
is equal to the index of the subsets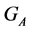 ; that is:
; that is:
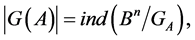 (1)
(1)
where 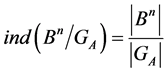 is the index of the group
is the index of the group 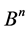 in regard to the subsets
in regard to the subsets .
.
Example.
1) Let  be a subgroup in
be a subgroup in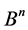 , and
, and 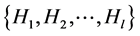 be the family of cosets of the subgroup
be the family of cosets of the subgroup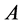 , and
, and

If we form the set:
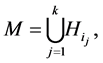
out of an arbitrary collection of the cosets , then
, then 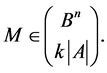
Let  and
and 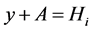 be an arbitrary cosets to the subgroup
be an arbitrary cosets to the subgroup ; then
; then  Consequently, any element of the group,
Consequently, any element of the group, 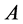 , belongs to the stabilizer of the set
, belongs to the stabilizer of the set , and thus:
, and thus:  and
and 
This example will be used in the sequel.
As (1) shows, to define the cardinality of the transitive set 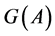 it is sufficient to know the cardinality of the stabilizer
it is sufficient to know the cardinality of the stabilizer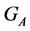 .
.
Let us note that the group  acts on the given set
acts on the given set , that is,
, that is,  is a stabilizer and we can use the same way of argumentation as we did above.
is a stabilizer and we can use the same way of argumentation as we did above.
If , then the transitive set
, then the transitive set 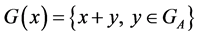 is defined in the standard way and:
is defined in the standard way and:
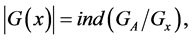 (2)
(2)
where 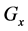 is the stabilizer of the element,
is the stabilizer of the element,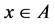 . Taking into account that:
. Taking into account that:
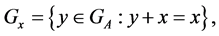
we have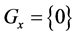 , for all
, for all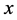 . Then we have from (2):
. Then we have from (2):

that is,  is equal to the index of the unit subgroup E, or:
is equal to the index of the unit subgroup E, or:
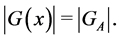
Lemma 1. The following comparison holds:

This immediately follows from the formula of the partition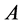 :
:
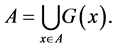
If  is the power index of the prime number
is the power index of the prime number , which is included in the canonic presentation
, which is included in the canonic presentation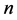 , then the following statements hold true:
, then the following statements hold true:
Corollary 1. The following inequality holds true:
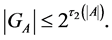
Corollary 2. The stabilizer 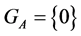 for any
for any 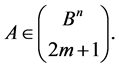
Corollary 3. Let 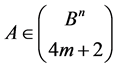 and
and 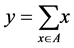 Then either
Then either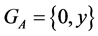 , or
, or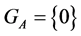 .
.
Lemma 2. The stabilizer  for an arbitrary set
for an arbitrary set 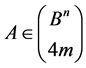 if
if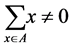 .
.
Proof. We assume, 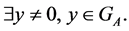 Then the elements of the set
Then the elements of the set  satisfy the following system:
satisfy the following system:
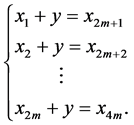
Adding up all the equations of the system, we get the following equality:  From this it follows that:
From this it follows that:  which is a contradiction and it proves the Lemma.
which is a contradiction and it proves the Lemma.
In the general case, if the element  belongs to the stabilizer
belongs to the stabilizer  of the subsets
of the subsets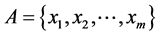 , the following holds true (according to the definition):
, the following holds true (according to the definition):
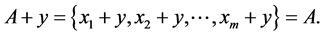 (3)
(3)
Let 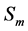 be a symmetrical group of the degree
be a symmetrical group of the degree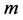 . We denote the elements of the group
. We denote the elements of the group 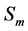 corresponding to transformation (3) by
corresponding to transformation (3) by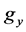 . Consequently, the element
. Consequently, the element  should by written as follows:
should by written as follows:
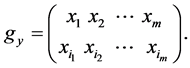
We consider the expansion 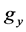 into a product of independent cycles:
into a product of independent cycles:
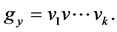 (4)
(4)
Lemma 3. If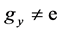 , then
, then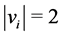 ,
, .
.
Proof. If , we have from (4):
, we have from (4):
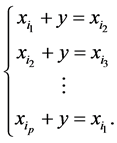 (5)
(5)
It follows from (5) that:
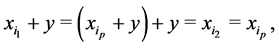
that is, 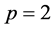 Q. E. D.
Q. E. D.
To calculate the stabilizer one has to consider the multiset:

which has a key role for the further considerations.
Let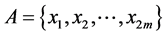 , and:
, and:
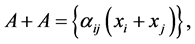
where 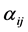 is the multiplicity of the inclusion of the element,
is the multiplicity of the inclusion of the element, 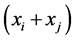 , into
, into .
.
Lemma 4. The stabilizer , of the set
, of the set , is the sets of elements
, is the sets of elements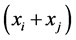 , where each occurs m times plus the zero element.
, where each occurs m times plus the zero element.
Proof. Let 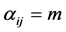 then the following holds true:
then the following holds true:

Two different  pairs:
pairs: 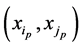 and
and , have no common elements; otherwise they coinside.
, have no common elements; otherwise they coinside.
Thus, the set of pairs 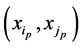 form the partition
form the partition , and the point y belongs to
, and the point y belongs to , according to Lemma 3.
, according to Lemma 3.
From Lemma 4 a simple algorithm for building the stabilizer 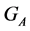 follows and, as a matter of fact, it is reduced to building of the multiset,
follows and, as a matter of fact, it is reduced to building of the multiset, . Complexity of such an algorithm is
. Complexity of such an algorithm is , where
, where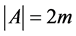 . The volume of the input information is the length of the recording of the set
. The volume of the input information is the length of the recording of the set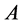 , that is,
, that is,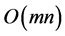 .
.
Lemma 5. If the cardinality of the subsets 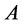 and that of the stabilizer
and that of the stabilizer 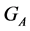 satisfy the following conditions:
satisfy the following conditions:
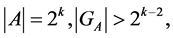
then:
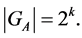
Proof. Let  For any
For any 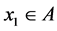 we build the set
we build the set . We choose any element
. We choose any element 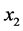 from
from 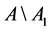 and define the set
and define the set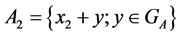 . We assume that there exists
. We assume that there exists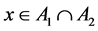 . Then the vector
. Then the vector  can be represented in two ways, namely:
can be represented in two ways, namely:
 and
and 
where . Consequently, we get:
. Consequently, we get: , which contradicts the choice of the element
, which contradicts the choice of the element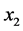 . Hence, the following holds true:
. Hence, the following holds true:
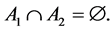 (6)
(6)
Taking into account that 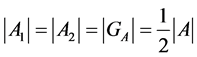 we have:
we have:
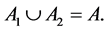 (7)
(7)
We denote . Taking into account that
. Taking into account that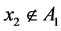 , we have:
, we have: . It follows from (6) and (7) that
. It follows from (6) and (7) that  is represented either in the form:
is represented either in the form:
 , or
, or 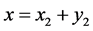
where . If
. If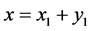 , then
, then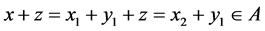 . It can be proved in the same way that
. It can be proved in the same way that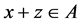 , for the case,
, for the case, 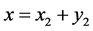 , Consequently,
, Consequently,  We got a contradiction and it concludes the proof of Lemma 5 if we take into account Lemma 1.
We got a contradiction and it concludes the proof of Lemma 5 if we take into account Lemma 1.
Lemma 5 is a useful tool for calculation of the stabilizer 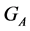 for
for . Its content can be interpreted as follows. If it is possible to define
. Its content can be interpreted as follows. If it is possible to define  elements belonging to
elements belonging to , then, taking into account that the cardinality of a stabilizer is an exponent with the base 2, we directly get:
, then, taking into account that the cardinality of a stabilizer is an exponent with the base 2, we directly get: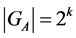 .
.
Examples.
2) If , then
, then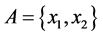 . Consequently,
. Consequently, . Taking Lemma 4 into account, we get:
. Taking Lemma 4 into account, we get:
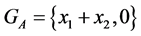
3) If 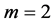 then
then 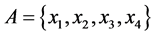 Consequently:
Consequently:
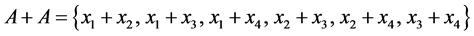
All the partitions into pairs of the set  are generated by one of them, for instance:
are generated by one of them, for instance:

It follows from this that if:

then the following equalities hold true:
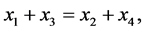
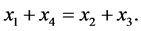
Consequently, the following statement holds true:
Statement 1. If  then
then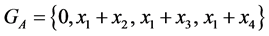 , But if
, But if 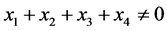 then
then 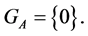
Examples.
4) Let  Then:
Then:
 and
and .
.
5) Let 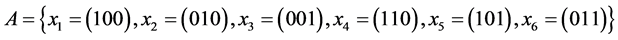 Then:
Then:
 And as
And as 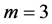 then:
then: 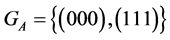
Now let us calculate the number of the sets that are transitive in regard to the group  The tool for such calculation is Burnside’s Lemma: [1] [2] .
The tool for such calculation is Burnside’s Lemma: [1] [2] .
Lemma (Burnside’s) 6. The number 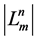 of the equivalence classes or transitive sets is as follows:
of the equivalence classes or transitive sets is as follows:
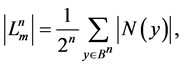
where  is the set of the (stationary) points
is the set of the (stationary) points 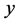 of the transformation, that is:
of the transformation, that is:
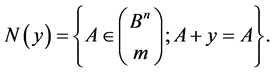
Lemma 7. The number of the solutions 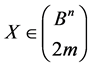 of the following equation:
of the following equation:
 (8)
(8)
is , if
, if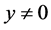 .
.
Proof. According to Lemma 3, Equation (8) is equivalent to the system of the following equations:
 (9)
(9)
where the partition  is chosen for the sake of certainty. Let us note that the following equation:
is chosen for the sake of certainty. Let us note that the following equation:
 (10)
(10)
has exactly  solutions for
solutions for  and it does not depend on
and it does not depend on  if
if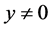 . Indeed, choosing an
. Indeed, choosing an 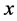 we get:
we get: . Further, if
. Further, if  and
and 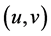 are two solutions of Equation (10), then either these solutions do not overlap, or they coinside. Indeed, we get
are two solutions of Equation (10), then either these solutions do not overlap, or they coinside. Indeed, we get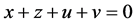 , from
, from 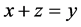 and
and ; consequently, it follows from
; consequently, it follows from  that
that  In the same way, if
In the same way, if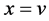 , then
, then 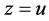 Thus, all the solutions of system (9) can be obtained by choosing
Thus, all the solutions of system (9) can be obtained by choosing 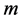 pairs from
pairs from 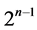 pairs, which are solutions of (10).
pairs, which are solutions of (10).
Theorem 1. The following equalities are valid:
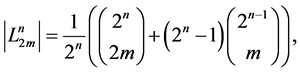 (11)
(11)
 (12)
(12)
Proof. We get from Burnside’s Lemma:
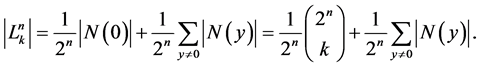
Then, for the case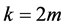 , taking into account Lemma 7, we get:
, taking into account Lemma 7, we get:
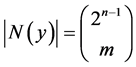
For . This directly proves Formula (11).
. This directly proves Formula (11).
For the case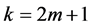 , taking into account Corollary 2, we get:
, taking into account Corollary 2, we get: 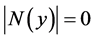 for all
for all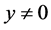 , which proves formula (12).
, which proves formula (12).
Thus, the above statements make, more or less, possible to know the structure of the stabilizer 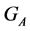 of the set
of the set
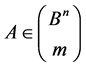 and to find the number of the transitive sets
and to find the number of the transitive sets 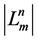 which are generated by the action of the group
which are generated by the action of the group  on
on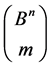 .
.
Let us also note that, according to Corollary 1, 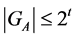 , if
, if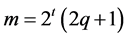 , where
, where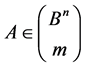 . On the other hand, as Example 1 shows, for any subgroup
. On the other hand, as Example 1 shows, for any subgroup 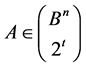 and for any collection of contiguous classes
and for any collection of contiguous classes  of the group
of the group  in regard to
in regard to 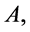 then the set
then the set  is in the family
is in the family 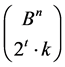 and
and 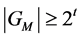
For an odd 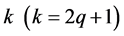 the cardinality of the set
the cardinality of the set 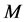 is equal to
is equal to , and its stabilizer
, and its stabilizer  has
has  elements. This shows that it is possible to draw the above mentioned boundary for the stabilizers of the considered sets. The following example of a contiguous class
elements. This shows that it is possible to draw the above mentioned boundary for the stabilizers of the considered sets. The following example of a contiguous class 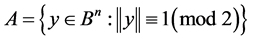 with the stabilizer
with the stabilizer 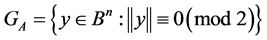 illustrates the above mentioned considerations, because
illustrates the above mentioned considerations, because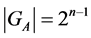 . Thus, the estimate
. Thus, the estimate  for the case
for the case 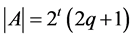 is not so bad evaluation for the cardinality of the stabilizer of the set
is not so bad evaluation for the cardinality of the stabilizer of the set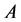 . The “average” value of this boundary in the whole interval of the cardinalities
. The “average” value of this boundary in the whole interval of the cardinalities , is
, is 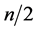 and this can serve as a “realistic” boundary for the cardinality of the stabilizer for a uniform distribution on the family of the sets
and this can serve as a “realistic” boundary for the cardinality of the stabilizer for a uniform distribution on the family of the sets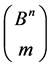 .
.
The family  of all transitive sets
of all transitive sets , where
, where , generates the partition
, generates the partition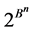 :
:
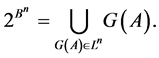 (13)
(13)
As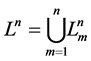 , then, according to Theorem 1, we have for the numbers
, then, according to Theorem 1, we have for the numbers 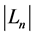 of the transitive sets the following equality:
of the transitive sets the following equality:
Corollary 4.
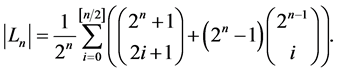
Shifts and Additive Channels. One of the applications of the above considerations are the so called additive channels.
We call any subsets 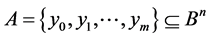 additive channel [3] [4] , if it carries out the following dictionary function:
additive channel [3] [4] , if it carries out the following dictionary function:
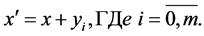 (14)
(14)
Thus, any word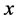 , if transmitted through the additive channel
, if transmitted through the additive channel , is transformed into one of the words
, is transformed into one of the words 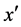 of (14), in the result of the shift by the vector
of (14), in the result of the shift by the vector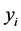 .
.
Definition 1 [5] . We define the  th order neighbourhood of the vector,
th order neighbourhood of the vector, 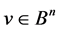 , in regard to
, in regard to , as follows:
, as follows:
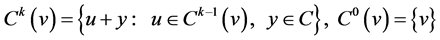 .
.
Definition 2. The code,  , corrects the errors of the additive channel
, corrects the errors of the additive channel  if the following condition holds true:
if the following condition holds true:
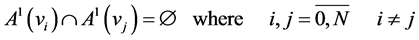 .
.
The equivalent definition has the following form: The code 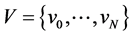 corrects the errors of the additive channel
corrects the errors of the additive channel 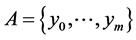 if the following condition holds true:
if the following condition holds true:
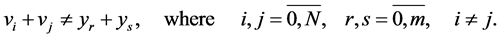 (15)
(15)
As the 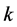 order cardinality does not depend on the vector
order cardinality does not depend on the vector  we denote:
we denote:
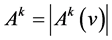 .
.
Let us note that for the cardinality of the code  correcting the errors of the additive channel
correcting the errors of the additive channel 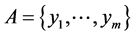 the following boundaries hold true [3] [4] :
the following boundaries hold true [3] [4] :
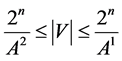 (16)
(16)
Actually, condition (15) makes possible to decode the initial message at the channel output through a standard “decoding table” of any word.
If one takes the sphere of radius t with the centre at zero as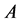 , then he gets the classic channel through which there take place no more than t distortions of the form:
, then he gets the classic channel through which there take place no more than t distortions of the form: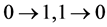 .
.
The main problem when investigating a given additive channel 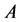 is the building the code
is the building the code 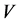 of the maximum cardinality, correcting the errors of the channel
of the maximum cardinality, correcting the errors of the channel . Consequently, each additive channel generates its own coding theory, and the possibilities of examining and sorting out all these communication tools are rather limited. At the same time, some most simple considerations show that many of these additive channels are equivalent (identical) in the sense of their content. Indeed, the channels,
. Consequently, each additive channel generates its own coding theory, and the possibilities of examining and sorting out all these communication tools are rather limited. At the same time, some most simple considerations show that many of these additive channels are equivalent (identical) in the sense of their content. Indeed, the channels,  and
and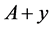 , are equivalent for any
, are equivalent for any , in the sense that any code
, in the sense that any code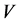 ,correcting the errors of the additive channel
,correcting the errors of the additive channel 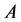 corrects the errors of the additive channel
corrects the errors of the additive channel 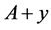 as well, and vice versa. The above classification of the additive channels is based on these considerations. In particular, one can always consider that
as well, and vice versa. The above classification of the additive channels is based on these considerations. In particular, one can always consider that 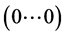 belongs to the channel
belongs to the channel 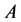 otherwise one could pass to the equivalent channel including the zero vector, without any loss of generality.
otherwise one could pass to the equivalent channel including the zero vector, without any loss of generality.
Another definition of equivalence of additive channals is directly connected with the error correcting code.
Let  be a predicate given on the Cartesian product
be a predicate given on the Cartesian product 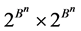 or:
or:
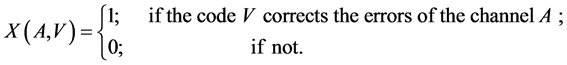
Definition 3 [5] . The two additive channels 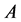 and
and 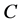 are equivalent if the following condition holds true for all
are equivalent if the following condition holds true for all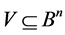 :
:
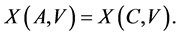 (17)
(17)
Actually, condition (17) means that if the code  corrects the errors of the channel
corrects the errors of the channel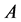 , then the code
, then the code 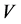 corrects the errors of the channel
corrects the errors of the channel 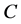 as well, and vice versa. In particular, if:
as well, and vice versa. In particular, if:
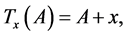
(that is, 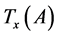 is a shift transformation) then:
is a shift transformation) then:

for any pair of points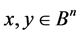 ,where the tilde sign
,where the tilde sign 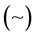 means the notion of equivalence introduced above.
means the notion of equivalence introduced above.
We denote the equivalence class including the channel 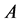 by
by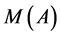 .
.
Example. 
One easily can see that these channels are equivalent though 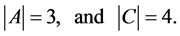
Actually, in the general case, the channel cardinality is not any obstacle for classification and, in some certain cases, it defines the channel equivalence one to one.
Statement 2. For any channel 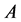 with the cardinality
with the cardinality 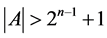 the followingtakes place:
the followingtakes place:
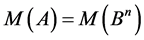 .
.
Proof. It follows from (16) that any code  for which either
for which either , or
, or , is consisted of one vector. On the other hand, for any code
, is consisted of one vector. On the other hand, for any code 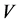 consisted of one vectorthe following equality is valid:
consisted of one vectorthe following equality is valid:
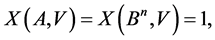
that is:
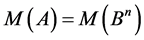 .
.
Q. E. D.
Note that the following example excludes the possibility of the contrary statement.
Example.
7) Let: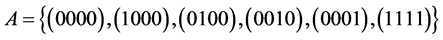 . Then:
. Then: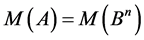 , if
, if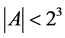 .
.
Now let us go back to Example 6. We have:

It is obvious that this example is not an exception; therefore, we can use the following equality:
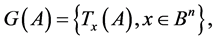
where  is the transitive set of the channel
is the transitive set of the channel  in regard to the group of transformation
in regard to the group of transformation . We get:
. We get:
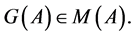
Taking into account (13), we state the following:
Theorem 2. For any channel  there exist the channels
there exist the channels 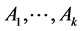 from
from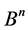 , such that the partition
, such that the partition
 is unique.
is unique.
This theorem shows the connection between the classes of equivalence for communication channels and the transitive sets of subsets , which are generated through the the action of the group
, which are generated through the the action of the group  on them.
on them.
Though the expansion of 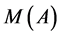 is unique, the transitive sets included in the expansion are generated by different collections of “basic” channels,
is unique, the transitive sets included in the expansion are generated by different collections of “basic” channels,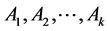 .
.
We reduced the investigation of communication channels to the investigation of transitive sets, and thus the investigation of the latter is reduced to that of the classes of equivalence, which can further be described introducing the relations of partial order:

Consequently, we came to the necessity of introducing of an invariant of an equivalence class, characterizing the given order.
An invariant of any  is the set
is the set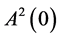 , including the zero vector, and this is its difference from the set
, including the zero vector, and this is its difference from the set 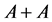 which was defined above.
which was defined above.
Theorem 3. For any channels 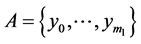 and
and 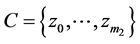 the following holds:
the following holds:

Proof. Let: , and the code
, and the code 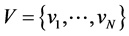 corrects the errors of the channel
corrects the errors of the channel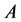 . Then, taking into account (15), we have:
. Then, taking into account (15), we have:

Consequently, 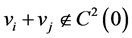 , which means that the code
, which means that the code 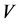 corrects the errors of the channel
corrects the errors of the channel .
.
If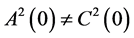 , then—without any loss of generality—we can assume that there exist
, then—without any loss of generality—we can assume that there exist  and
and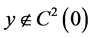 . We consider the code
. We consider the code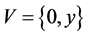 . Let us show that
. Let us show that 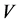 corrects the errors of the channel
corrects the errors of the channel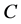 , but does not correct the errors of the channel
, but does not correct the errors of the channel . To prove this it is sufficient to show that both channels
. To prove this it is sufficient to show that both channels  and
and 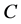 include the zero point, and it can be done applying the shift transformation. Obviously, this transformation does not change the sets
include the zero point, and it can be done applying the shift transformation. Obviously, this transformation does not change the sets  and
and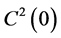 . The code
. The code  corrects the errors of the channel
corrects the errors of the channel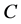 , because:
, because:

But , that is,
, that is,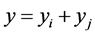 . Hence:
. Hence:
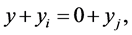
that is, the code 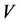 does not correct the errors of A. Q. E. D.
does not correct the errors of A. Q. E. D.
Unfortunately, the answer to the question: “is every set from 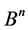 invariant under action of any equivalence class” is negative. For instance, all sets having cardinality 3 or 5 have no invariants from Bn .
invariant under action of any equivalence class” is negative. For instance, all sets having cardinality 3 or 5 have no invariants from Bn .
Statement 3. An equivalence class does not include more than one group.
Proof. Let the channels, 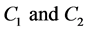 be groups from
be groups from . It follows from the following obvious equalities:
. It follows from the following obvious equalities:

that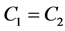 . Q. E. D.
. Q. E. D.
Statement 4. If the group, 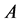 , is the equivalence class invariant of some channel
, is the equivalence class invariant of some channel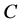 , then
, then  and it has the maximum cardinality in that equivalence class.
and it has the maximum cardinality in that equivalence class.
In other words, a group channel is a “preferable generator” in its equivalence class.
Concluding, we note that the preceding definitions are symmetrical in regard to the pair 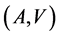 and, consequently, both the generation and correction of errors have the same essence. It means that all statements in regard to the communication channels
and, consequently, both the generation and correction of errors have the same essence. It means that all statements in regard to the communication channels  hold true in regard to the codes
hold true in regard to the codes  of the pair
of the pair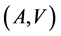 .
.
References
- Lang, S. (1968) Algebra (in Russian). Moscow, Mir.
- Sachkow, W.N. (1977) Combinatric Methods of Descret Mathematics (in Russian). Nauka, Moscow.
- Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2006) Perfect Codes in Additive Channels. Reports of RAS, 411, 306-309 (in Russian).
- Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2008) On Perfect Codes in Additive Channels. Problems of Information Transmission, 44, 12-19.
- Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2010) Correction of Errors in an Additive Channel. Vol. 2, Westnik RAU, 12-25 (in Armenian).

