Open Journal of Discrete Mathematics
Vol.4 No.1(2014), Article ID:42402,10 pages DOI:10.4236/ojdm.2014.41003
Equidistribution in Sharing Games
Carlos D’Andrea1, Emiliano Gómez2
1Departament d’Àlgebra i Geometria, Universitat de Barcelona, Barcelona, Spain
2Department of Mathematics, University of California, Berkeley, Berkeley, USA
Email: cdandrea@ub.edu, emgomez@math.berkeley.edu
Copyright © 2014 Carlos D’Andrea, Emiliano Gómez. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Carlos D’Andrea, Emiliano Gómez. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received August 30, 2013; revised September 25, 2013; accepted October 12, 2013
ABSTRACT
Games often provide a good introduction to interesting phenomena in mathematics. In this note, we examine three variations of an iterative sharing game played around a circular (or not so circular) table. More precisely, for each variation, we study the tendency toward equal distribution among the players. In the first variation, the players have discrete amounts at each step. The second variation removes this restriction, and the third one considers an infinitely long table with an infinite number of players.
Keywords: Equidistribution; Iteration; Linear Transformation; Limit Distribution
1. Sharing around a Table with Discrete Amounts
Suppose you have 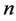 persons seated around a circular table, each having an even number of dimes. Number them from 1 to
persons seated around a circular table, each having an even number of dimes. Number them from 1 to 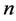 counterclockwise, and denote by
counterclockwise, and denote by 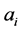 the (even) number of dimes that the i-th person has,
the (even) number of dimes that the i-th person has, 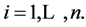
The game is played by repeating the same two steps over and over, as follows: first, each person gives one half of her dimes to the person sitting on her right. In symbols,
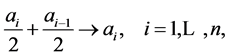 (1)
(1)
with the convention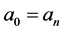 . Note that the new
. Note that the new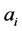 ’s are not all necessarily even. The second step, which allows us to repeat (1), is to add one dime to each odd
’s are not all necessarily even. The second step, which allows us to repeat (1), is to add one dime to each odd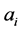 :
:
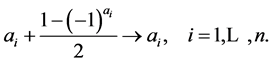 (2)
(2)
We call this game the “discrete sharing game”.
Proposition 1.1 By iterating (1) and (2), after a finite number of steps, we will have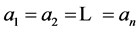 , i.e. every person ends up with the same number of dimes.
, i.e. every person ends up with the same number of dimes.
This problem can be found in [1]. The proof follows easily from two observations. First, the maximum amount around the table cannot increase, nor can the minimum amount decrease. Second, if the minimum amount is strictly smaller than the maximum amount, then after the next step, either the minimum amount will have increased, or else the number of players having the minimum amount will have decreased. Together, these observations imply that after finitely many steps, the maximum and minimum amounts will coincide. We leave the details of the proof to the reader. Another interesting problem is to determine the number of iterations needed to reach equidistribution in terms of the initial data (see Figures 1, 2 and 3).
An iterative sharing game that tends toward the equal distribution of the players’ amounts is what we call an
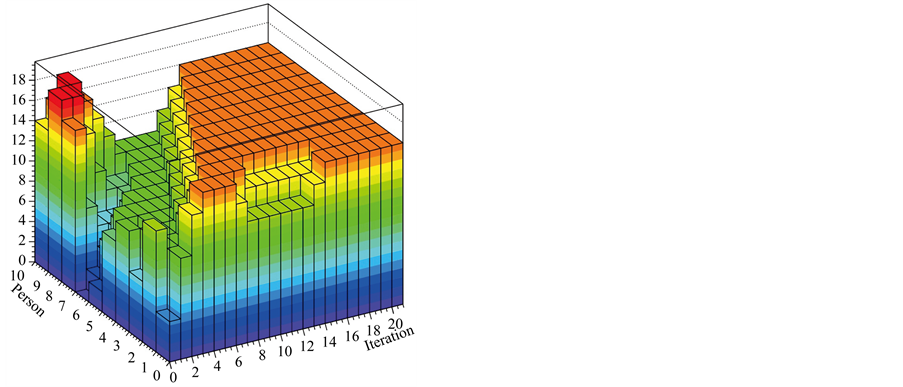
Figure 1. 3-D graph of the discrete sharing game with 10 players and with initial distribution as shown. In this example, equidistribution is achieved at the 16-th iteration.
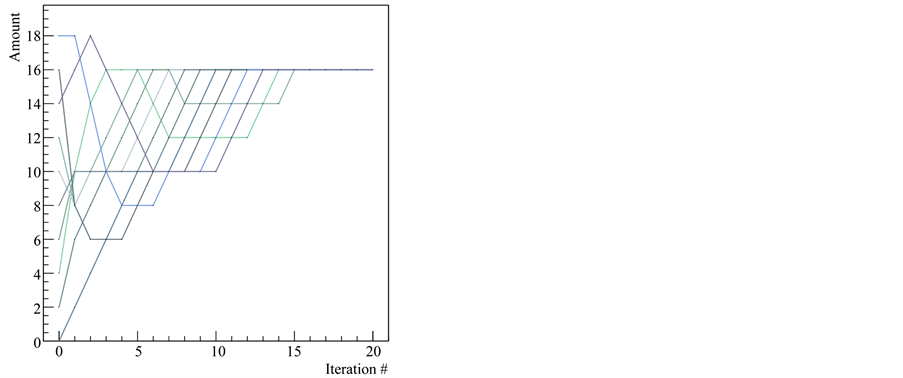
Figure 2. 2-D graph of the game given in Figure 1. This graph does not show how the initial amounts are distributed around the table.
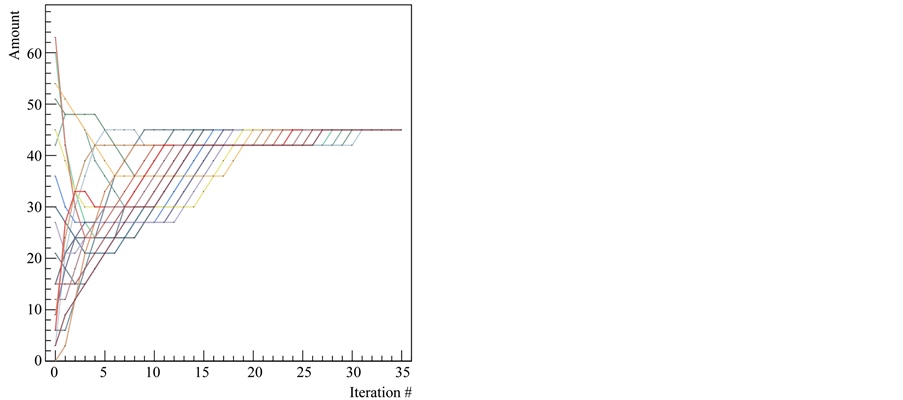
Figure 3. 2-D graph of a generalized discrete sharing game with 20 players and k = 3.
“equidistribution process”. You may think that in the above example, the equidistribution is due to the fact that the sharing is done by halves. However, Proposition 1.1 generalizes without much effort: suppose all the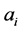 ’s are initially multiples of a fixed number
’s are initially multiples of a fixed number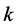 . Replace (1) with
. Replace (1) with
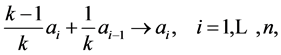
and (2) with a similar step where you add dimes until you reach the first multiple of  greater than or equal to
greater than or equal to 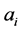 for all
for all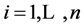 . Then again you will end up with
. Then again you will end up with  after a finite number of steps.
after a finite number of steps.
2. Sharing around a Table with Complex Numbers
Suppose there are 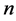 persons around a circular table, numbered counterclockwise as before. But this time each of them starts with an initial amount
persons around a circular table, numbered counterclockwise as before. But this time each of them starts with an initial amount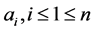 , that can be any complex number. Let
, that can be any complex number. Let 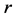 be a positive real number,
be a positive real number,![]() . It will play the role of
. It will play the role of 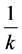 above. We want to study the behavior of
above. We want to study the behavior of
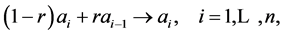
as the number of iterations goes to infinity. Note that the balancing step (2) does not make sense here anymoreas neither the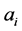 ’s are necessarily integers nor
’s are necessarily integers nor  for some
for some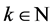 . We can give a realistic feeling to the game if we restrict the
. We can give a realistic feeling to the game if we restrict the ’s to real numbers. Then at each step, each person is sharing her wealth
’s to real numbers. Then at each step, each person is sharing her wealth 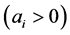 or debt
or debt 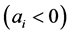 by giving a portion
by giving a portion  of her number to the person on her right. But this restriction is unnecessary, so we will work in the more general setting of complex numbers. In contrast to the discrete version of the last section, we call this the “complex sharing game”.
of her number to the person on her right. But this restriction is unnecessary, so we will work in the more general setting of complex numbers. In contrast to the discrete version of the last section, we call this the “complex sharing game”.
For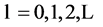 , let
, let ![]() be the amount that person
be the amount that person ![]() has after the
has after the  -th step. Then
-th step. Then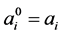 , and we also extend the definition by setting
, and we also extend the definition by setting ![]() whenever
whenever , so that
, so that ![]() makes sense for any integer i. The rule for sharing at each step then yields
makes sense for any integer i. The rule for sharing at each step then yields
![]() (3)
(3)
where the sub-indices are understood modulo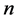 .
.
Note that if![]() , then
, then 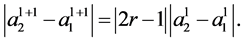 Since
Since 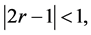 clearly this sharing game with only two people is an equidistribution process. This is particularly trivial if
clearly this sharing game with only two people is an equidistribution process. This is particularly trivial if 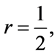 in which case both persons will have the same number after just one step. From now on, we assume
in which case both persons will have the same number after just one step. From now on, we assume![]() . Note also that the sum of the numbers around the table remains constant with each step. Let us denote this constant by
. Note also that the sum of the numbers around the table remains constant with each step. Let us denote this constant by![]() , that is
, that is

2.1. The Sharing Transformation and Its Eigenvalues
We can model the sharing process (3) with the aid of the  -linear transformation
-linear transformation 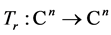 given by
given by
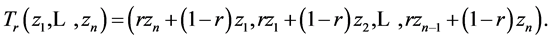
With the notation as above, we see that 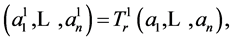 where the exponent on
where the exponent on  indicates the number of times that this transformation is composed with itself:
indicates the number of times that this transformation is composed with itself: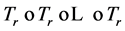 .
.
In the canonical basis of ,
, 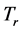 has matrix
has matrix
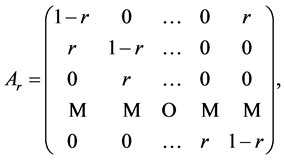
which has entries  along the main diagonal,
along the main diagonal, 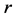 on the diagonal immediately below and at the upper right corner, and zero elsewhere. This is a “stochastic” or “Markov” matrix, as its entries are all non-negative and the sum of the entries in each row is equal to 1. For more information on these matrices and their interesting properties, we refer the reader to [2]. We will presently prove some of these properties for our matrix
on the diagonal immediately below and at the upper right corner, and zero elsewhere. This is a “stochastic” or “Markov” matrix, as its entries are all non-negative and the sum of the entries in each row is equal to 1. For more information on these matrices and their interesting properties, we refer the reader to [2]. We will presently prove some of these properties for our matrix  in order to make this note more self-contained, but the reader should be aware that both Propositions 1.1 and Theorem 2.2 below hold for any stochastic matrix.
in order to make this note more self-contained, but the reader should be aware that both Propositions 1.1 and Theorem 2.2 below hold for any stochastic matrix.
Proposition 2.1 The matrix 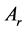 has n distinct eigenvalues
has n distinct eigenvalues 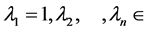 with
with  for
for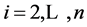 .
.
Proof. Let 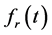 be the characteristic polynomial of
be the characteristic polynomial of 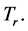 Computing it explicitly, we obtain
Computing it explicitly, we obtain
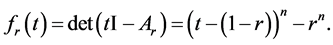
Let  be the nth distinct complex roots of
be the nth distinct complex roots of  Then it is easy to see that the
Then it is easy to see that the  (distinct) roots of
(distinct) roots of ![]() are
are
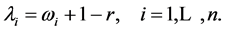
If we set 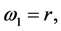 then we have that
then we have that  For
For 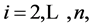 we have
we have 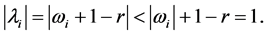 The inequality is strict, as
The inequality is strict, as ![]() is not a positive real number if
is not a positive real number if ![]() □
□
An eigenvector associated to the eigenvalue 1 is 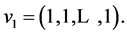 In our game, this eigenvector corresponds to the case where every person has the same amount
In our game, this eigenvector corresponds to the case where every person has the same amount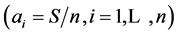 . Clearly, this situation is stable, i.e. does not change after applying
. Clearly, this situation is stable, i.e. does not change after applying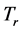 . Let
. Let 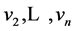 denote eigenvectors for the eigenvalues
denote eigenvectors for the eigenvalues 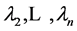 respectively. Thus
respectively. Thus 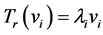 for each
for each ![]() Now we are ready for the main result of this section, which is that the complex sharing game also tends toward equal distribution among the
Now we are ready for the main result of this section, which is that the complex sharing game also tends toward equal distribution among the  players. (See Figures 4 and 5).
players. (See Figures 4 and 5).
Theorem 2.2 The complex sharing game described by (3) is an equidistribution process. That is,
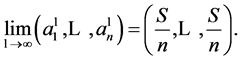
Proof. Note that  is a basis for
is a basis for  consisting of eigenvectors of
consisting of eigenvectors of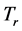 . Write
. Write
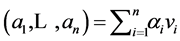 with
with . Then
. Then
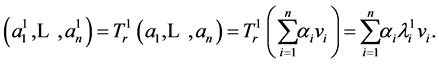
Proposition 2.1 now implies that
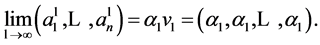
Therefore the game is indeed an equidistribution process. □
Note that, since the sum of the n numbers remains constant at each step of the iteration above, we must have
 There is another way to obtain the value of
There is another way to obtain the value of![]() . Let
. Let 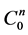 be the subspace of
be the subspace of 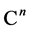 defined as
defined as 
Lemma 2.1 Let 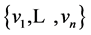 be the basis of eigenvectors fixed above. Then
be the basis of eigenvectors fixed above. Then  is a basis of
is a basis of 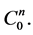
Proof. Write 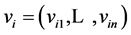 for
for![]() . Since
. Since 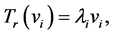 we have
we have
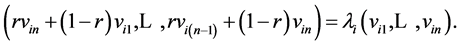
Adding the coordinates on each side of this identity, we get

Since  for
for  we conclude that
we conclude that  Therefore, the subspace spanned by
Therefore, the subspace spanned by  is contained in
is contained in ![]() and since both of these spaces have dimension
and since both of these spaces have dimension![]() , we must have equality, proving the claim. □
, we must have equality, proving the claim. □
We can use this statement to compute the value of![]() . We have
. We have

Recall that we chose  Since
Since , the sum of the coordinates of this vector is equal
, the sum of the coordinates of this vector is equal
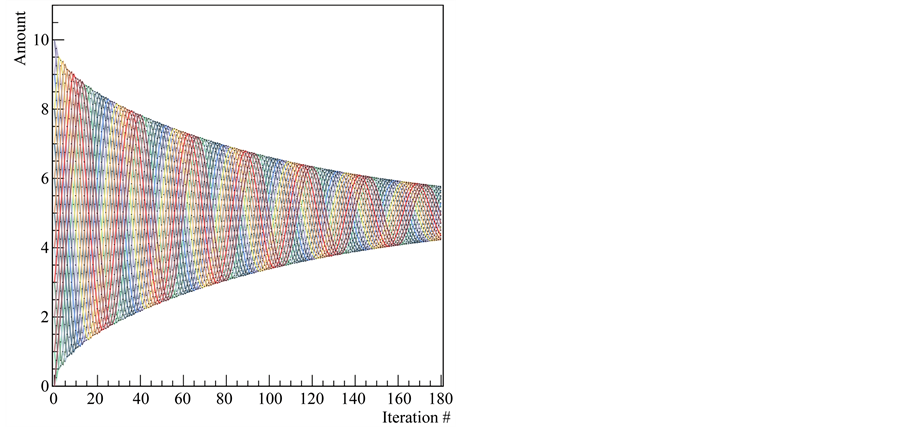
Figure 4. Evolution of the complex sharing game with 20 players and r = 3/4. The initial amounts are integers between 0 and 10.
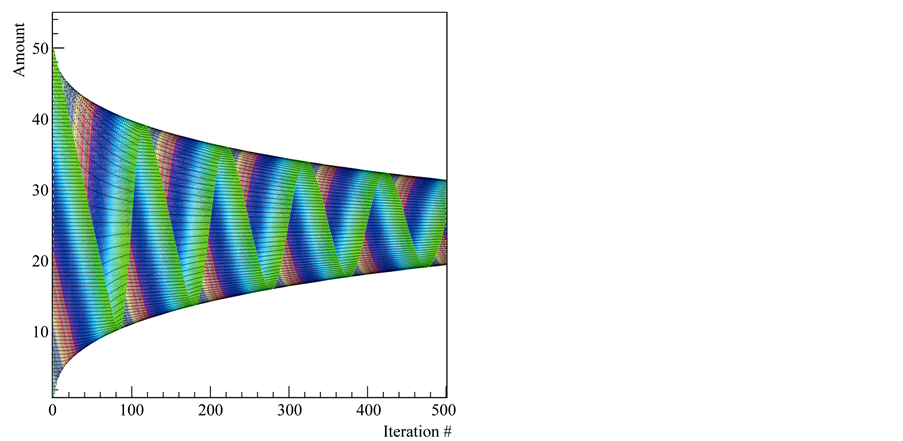
Figure 5. Evolution of the complex sharing game with 50 players and r = 1/2. The initial amounts are integers between 0 and 50.
to zero, and hence 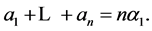 From this we deduce again that
From this we deduce again that

2.2. An Explicit Formula for ![]()
Recall that we defined![]() , and in particular
, and in particular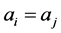 , whenever
, whenever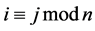 . Let us find a formula, in terms of the initial data
. Let us find a formula, in terms of the initial data , for the number that each person will have after any given step of the complex sharing game:
, for the number that each person will have after any given step of the complex sharing game:
Proposition 2.3 For any ![]() and
and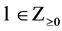 , we have
, we have
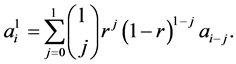
Proof. We use induction on , the initial step being obvious. Next, assume the formula holds for all
, the initial step being obvious. Next, assume the formula holds for all ![]() and for all
and for all ![]() with
with 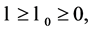 for a fixed
for a fixed![]() . Then,
. Then,
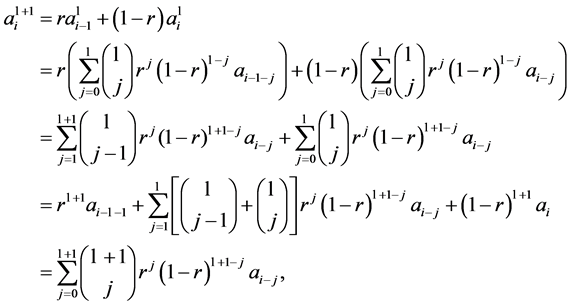
so the formula holds for 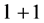 and the proof is complete. □
and the proof is complete. □
In particular, when each person shares one half of her amount at each step, we have Corollary. If 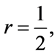 then
then 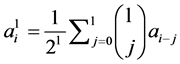 for all
for all ![]() and
and![]() .
.
By grouping the binomial coefficients 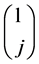 in congruence classes of j modulo n, we obtain an equivalent formulation of this result (always for
in congruence classes of j modulo n, we obtain an equivalent formulation of this result (always for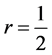 ):
):
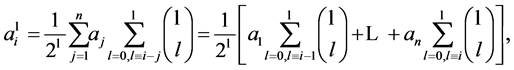
where each congruence is understood to be modulo 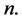 If all the initial amounts
If all the initial amounts 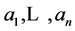 are equal, the sharing process is stable from the beginning, and this formula reduces to the well known fact about the sum of the entries in the
are equal, the sharing process is stable from the beginning, and this formula reduces to the well known fact about the sum of the entries in the  -th row of the Pascal triangle,
-th row of the Pascal triangle, . What is more interesting is that, in light of Theorem 2.2,
. What is more interesting is that, in light of Theorem 2.2,  for all i, regardless of the initial amounts. So given n, if we group the binomial coefficients
for all i, regardless of the initial amounts. So given n, if we group the binomial coefficients 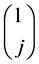 by the congruence classes of j modulo n and give each class an arbitrary weight, then as we go further down the rows of the Pascal triangle, the weighed sum of the entries divided by the sum with no weights,
by the congruence classes of j modulo n and give each class an arbitrary weight, then as we go further down the rows of the Pascal triangle, the weighed sum of the entries divided by the sum with no weights, ![]() , always tends to the average of the weights. More generally, regardless of the value of r, Theorem 2.2 shows that the sums given in the statement of Proposition 2.3 all tend to the same limit
, always tends to the average of the weights. More generally, regardless of the value of r, Theorem 2.2 shows that the sums given in the statement of Proposition 2.3 all tend to the same limit ![]() as
as ![]()
2.3. Eigenvectors of Tr and Vandermonde Matrices
Let 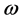 be any n-th root of unity, i.e.
be any n-th root of unity, i.e.  Then it is easy to check that
Then it is easy to check that
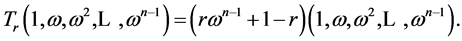
That is, 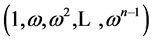 is an eigenvector of
is an eigenvector of  with eigenvalue
with eigenvalue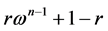 , the latter being of course one of the
, the latter being of course one of the  above.
above.
Therefore, if 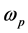 is a primitive n-th root of unity, then the vectors
is a primitive n-th root of unity, then the vectors 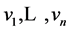 given by
given by
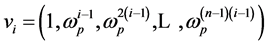
form a basis for 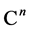 consisting of eigenvectors of
consisting of eigenvectors of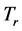 . Note that we have again
. Note that we have again 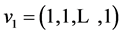 as above, and that the eigenvalue for
as above, and that the eigenvalue for 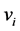 is
is 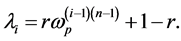
Under the (ordered) basis  has diagonal matrix
has diagonal matrix
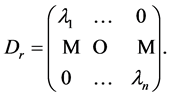
The matrix whose columns are the coordinates of the vectors  changes the basis from the canonical to
changes the basis from the canonical to . This is a Vandermonde matrix
. This is a Vandermonde matrix
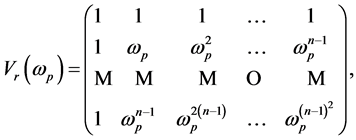
and it is well knwon that its inverse is another (normalized) matrix of the same type,
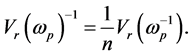
We can use this last matrix to express the vector of initial amounts 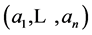 in terms of the basis
in terms of the basis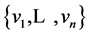 . As in the proof of Proposition 2, let
. As in the proof of Proposition 2, let 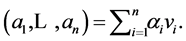 Then
Then

and a straightforward computation yields 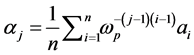 for
for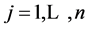 . This gives us yet another way to obtain
. This gives us yet another way to obtain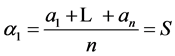 .
.
3. Sharing at an Infinite Table
Suppose now that, instead of a circular table, we have an infinite number of persons seated on one side of an infinitely long “rectangular” table , their number being unbounded both from the left and the right. Each person has an initial (complex number) amount to be shared in the same way as in the game with the circular table: at each step, each person gives a portion 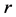 of her amount to the person on her right. As before, r is a fixed positive real number,
of her amount to the person on her right. As before, r is a fixed positive real number,![]() . We call this version the “infinite sharing game”.
. We call this version the “infinite sharing game”.
The initial data now is a sequence ![]() of complex numbers. We define
of complex numbers. We define ![]() as in (3) for
as in (3) for ![]() and
and![]() . Note that this time there is no “congruence modulo
. Note that this time there is no “congruence modulo 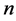 “, as there are infinitely many players, indexed by the integers. Indeed, the rectangular table can be regarded as the limit of circular tables having
“, as there are infinitely many players, indexed by the integers. Indeed, the rectangular table can be regarded as the limit of circular tables having  The recursion from sharing is the same as before:
The recursion from sharing is the same as before:
![]() (4)
(4)
Proposition 2.3 also holds here, and the proof is the same. The only difference is that now we do not have 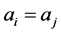 whenever
whenever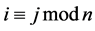 , the condition that effectively made the game circular (and with
, the condition that effectively made the game circular (and with 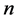 players) before. So we still get
players) before. So we still get
 (5)
(5)
This formula shows something that is obvious in the new context, namely that the amount of the person in the i-th place will depend only on the initial amounts of those people seated to her left (and on her own initial amount, of course). So there is no reason to believe that this new game should be an equidistribution process. For instance, if there is a concentration of wealth (by which we mean numbers with large absolute value) in some section of the table, it will never spread to the left. However, as the following result shows, if one of the sequences 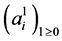 converges, then the game will tend toward equal distribution.
converges, then the game will tend toward equal distribution.
Theorem 3.1 If 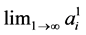 exists for some
exists for some![]() , then
, then ![]() exists for all
exists for all , and all of these limits coincide.
, and all of these limits coincide.
Proof. Let ![]() be such that
be such that 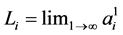 exists. Then, using (4), we have
exists. Then, using (4), we have
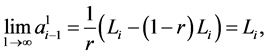
i.e. 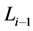 exists and it is equal to
exists and it is equal to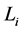 . By induction, we have then that
. By induction, we have then that 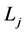 exists and
exists and 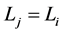 for all
for all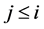 .
.
Now, using (4) again,
![]() (6)
(6)
for all![]() . Since
. Since 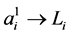 as
as![]() , given
, given ![]() there exists
there exists 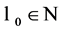 such that
such that 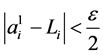 for all
for all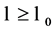 . But then we have that for
. But then we have that for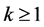 ,
,
 (7)
(7)
because
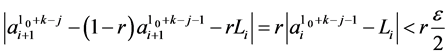
thanks to (6), and
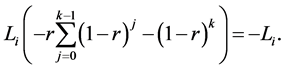
For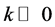 , we can get
, we can get  which, together with (7), shows that
which, together with (7), shows that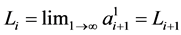 and from here we deduce (again by induction) that
and from here we deduce (again by induction) that ![]() for all
for all . □
. □
It would be an interesting problem to characterize those sequences ![]() of initial data that induce an equidistribution process in the infinite rectangular table. Note for instance that if
of initial data that induce an equidistribution process in the infinite rectangular table. Note for instance that if 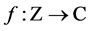 is any periodic function and we set
is any periodic function and we set 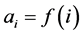 for
for![]() , then the game will be an equidistribution process (this is essentially the complex game around a circular table, where the number of players is the period of
, then the game will be an equidistribution process (this is essentially the complex game around a circular table, where the number of players is the period of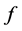 , “lifted” to the infinite rectangular table). One natural question to ask is this: if the initial data is bounded, must the infinite game be an equidistribution process? Suppose that
, “lifted” to the infinite rectangular table). One natural question to ask is this: if the initial data is bounded, must the infinite game be an equidistribution process? Suppose that 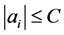 for all
for all![]() . Then, since
. Then, since
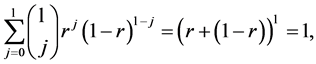 (8)
(8)
we see from (5) that 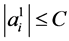 for all
for all ![]() and
and![]() . Does this imply that the sequence
. Does this imply that the sequence 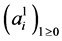 converges for some (and hence all)
converges for some (and hence all)![]() ? The answer is NO, as the following example shows.
? The answer is NO, as the following example shows.
Example 1 Suppose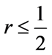 , and set
, and set
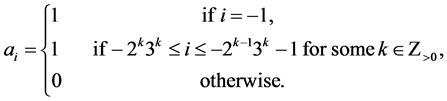
This sequence can be defined recursively by first setting all its values equal to zero for![]() , then
, then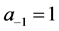 , and from there on we move to the left two zeroes, then three ones. Every time we end with a list of ones, we put a sequence of zeroes doubling in the number of the sequence already built so far (starting from
, and from there on we move to the left two zeroes, then three ones. Every time we end with a list of ones, we put a sequence of zeroes doubling in the number of the sequence already built so far (starting from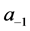 ). And every time we end with a list of zeroes, we put a sequence of ones equal to the number of the sequence already built so far (starting from
). And every time we end with a list of zeroes, we put a sequence of ones equal to the number of the sequence already built so far (starting from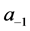 ), always moving to the left. So, the sequence looks like this (starting from
), always moving to the left. So, the sequence looks like this (starting from  on the right):
on the right):

With this sequence as the initial data and (5), one can show that for any positive integer ![]()

so the sequence 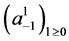 does not converge and, in light of Theorem 3.1,
does not converge and, in light of Theorem 3.1, 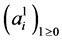 does not converge for any
does not converge for any![]() .
.
An immediate consequence of Theorem 3.1, is that if there exist  and
and ![]() such that
such that 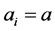 for all
for all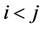 , then the infinite game is an equidistribution process. This is, in fact, a particular case of a more general fact: it turns out that equidistribution follows from the existence of
, then the infinite game is an equidistribution process. This is, in fact, a particular case of a more general fact: it turns out that equidistribution follows from the existence of 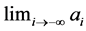 (and not, as we just saw, from the boundedness of
(and not, as we just saw, from the boundedness of![]() ).
).
Theorem 3.2 Suppose that . Then
. Then 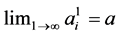 for every
for every![]() .
.
Proof. Consider the sequence ![]() defined as
defined as  for all
for all![]() . For a fixed
. For a fixed![]() , due to (4), it is easy to see that
, due to (4), it is easy to see that  if and only if
if and only if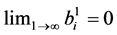 , so we can assume without loss of generality that
, so we can assume without loss of generality that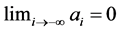 . For a fixed
. For a fixed![]() , since the sequence
, since the sequence  converges, there exists
converges, there exists ![]() such that
such that
 for all
for all . Let
. Let ![]() be given. Since
be given. Since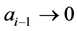 , there exists
, there exists 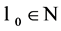 such that
such that  if
if
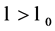 . For
. For , we use (5) to write
, we use (5) to write
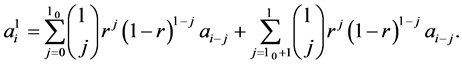 (9)
(9)
As 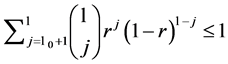 (because of (8)), we get easily
(because of (8)), we get easily

As for the first summand of (9), we have:

Since , for
, for ![]() we get
we get , and hence we can bound (9) as follows:
, and hence we can bound (9) as follows:
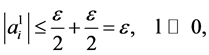
which proves that 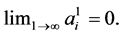 □
□
When the initial amounts are all real, ![]() , one can similarly show that if
, one can similarly show that if  (resp.
(resp.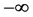 ), then
), then 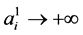 (resp.
(resp.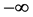 ) as
) as![]() , for every
, for every![]() .
.
Note that the existence of 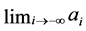 is sufficient but not necessary for the infinite game to be an equidistribution process. This can be seen from the above example where the initial data take on the values of a periodic function
is sufficient but not necessary for the infinite game to be an equidistribution process. This can be seen from the above example where the initial data take on the values of a periodic function . As mentioned above, it would be interesting to find more explicit necessary and sufficient conditions than the existence of
. As mentioned above, it would be interesting to find more explicit necessary and sufficient conditions than the existence of 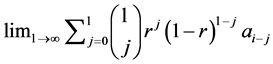 for some
for some![]() , which is essentially the characterization we get from Theorem 3.1 and (5).
, which is essentially the characterization we get from Theorem 3.1 and (5).
Acknowledgements
We are grateful to Adrián Paenza from whom we learnt about the discrete sharing game and the reference [1]. We would also like to thank José Ignacio Burgos for interesting discussions, Gervasio Gómez for programming several simulations and producing the figures, and Juan Sabia for suggesting the statement of Theorem 3.2 as it appears in the text, which is stronger and more general than what we had originally written.
The first author was partially supported by the research project MTM201020279 from the Ministerio de Ciencia e Innovacióon (Spain).
[1] REFERENCES
[2] G. Z. Chang and T. W. Sederberg, “Over and Over again,” New Mathematical Library, 39. Mathematical Association of America, Washington DC, 1997. xiv+309 pp. ISBN: 0-88385-641-7.
[3] G. Latouche and V. Ramaswami, “Introduction to Matrix Analytic Methods in Stochastic Modeling,” 1st Edition, PH Distributions, ASA SIAM, 1999.

