Open Journal of Discrete Mathematics
Vol.3 No.2(2013), Article ID:30468,7 pages DOI:10.4236/ojdm.2013.32017
The Software for Constructing Trails with Local Restrictions in Graphs
Department of Mathematical Methods in Economics and Statistics, South Ural State University, Chelyabinsk, Russian Federation
Email: kwark@mail.ru
Copyright © 2013 Tatyana Panyukova, Igor Alferov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 18, 2012; revised March 15, 2013; accepted April 20, 2013
Keywords: Eulerian Graph; Trail; Transition; Compatible Path; Algorithm
ABSTRACT
The present research considers the problem of covering a graph with minimal number of trails satisfying the pre-defined local restrictions. The research is devoted to the problem of graph covering by minimal number of trails satisfying some local restrictions. Algotithm of allowed Eulerian cycle construction is considered. The authors showed that it is possible to recognize the system of transitions and solve the problem of constructing the allowable path by linear time. It’s also possible to find allowable Eulerian cycle for Eulerian graph or to proclaim that such a cycle does not exist by the time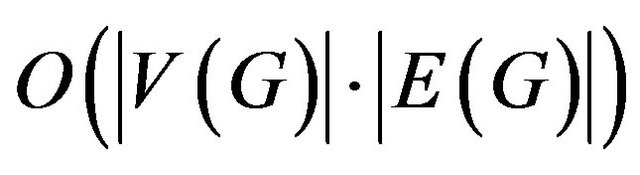 . All presented algorithms have the software realization.
. All presented algorithms have the software realization.
1. Introduction
Lots of problems of finding paths satisfying the different restrictions can be applied to some practical problems. For example for sheet material cutting problem plane graph represents the model of cutting plan, and a path covering all its edges defines the trajectory of cutter. The restriction defined for this problem is lack of intersection of any initial part of path with edges that are not passed yet [1]. Creating the control systems using non-oriented graphs the following problems of constructing the paths with different restrictions can arise. Among them are straight-ahead paths [2]; paths the next edge of which is defined by the given cyclic order on the set of incident edges [3-5]; paths for which it’s necessary to pass some edges in pre-defined order [5].
The restrictions on the order of vertices and edges can be classified as local (the next edge of a path is defined by conditions established at the current vertex or edge [2-8]), and global (Eulerian, Hamiltonian cycles, bidirectional double tracing etc.). Most of researches are devoted to algorithms with local restrictions of edges order in a path. The present research considers the problem of covering a graph with minimal number of trails satisfying the pre-defined local restrictions.
2. Constructing of TG-Compatible Path
The generalization of most of particular cases for problem of simple trail with local restrictions construction and analysis of its computing complexity is made by S.Szeider [7].
Let’s quote the basic definitions and results of this research to make the further statements clear. Let’s confine with finite simple graphs. Let’s designate as 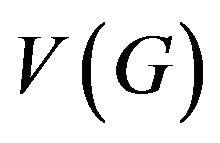 and
and 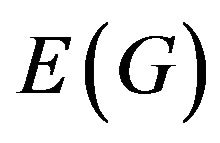 the sets of vertices and edges of graph G correspondingly. For vertex
the sets of vertices and edges of graph G correspondingly. For vertex 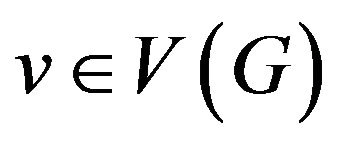 let’s define the set
let’s define the set 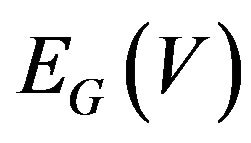 of all graph G edges incident to vertex v. The degree of vertex v let be designated as
of all graph G edges incident to vertex v. The degree of vertex v let be designated as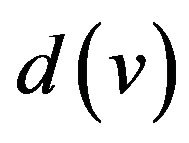 ; for
; for  let
let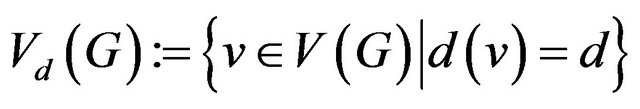 . Let
. Let 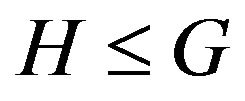 if H be vertex-induced subgraph of graph G i.e. the subgraph received of graph G by deleting of one set of vertices and only all edges incident to vertices of this set.
if H be vertex-induced subgraph of graph G i.e. the subgraph received of graph G by deleting of one set of vertices and only all edges incident to vertices of this set.
Restrictions for paths in graph G can be defined in terms of allowed transitions graph.
Definition 1. Let transition graph 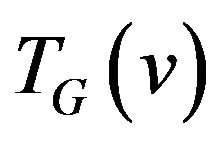 for vertex
for vertex 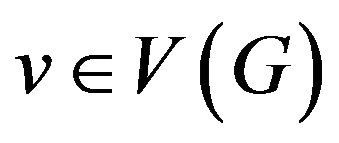 be a graph vertices of which are the edges incident to vertex v i.e.
be a graph vertices of which are the edges incident to vertex v i.e.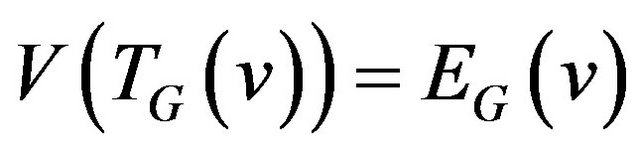 , and set of edges consists of allowed transitions.
, and set of edges consists of allowed transitions.
Definition 2. The system of allowed transitions (or shortly, system of transitions) 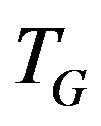 is called the set
is called the set 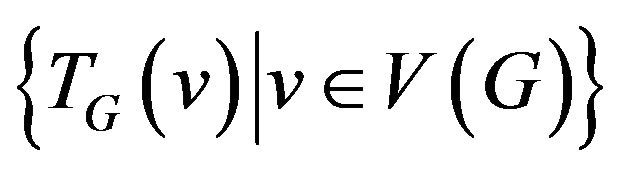 where
where 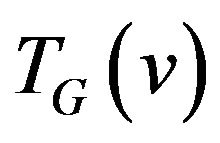 be the transition graph for vertex v.
be the transition graph for vertex v.
Definition 3. The path 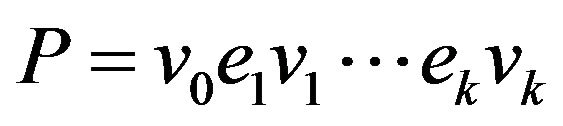 for graph G is called
for graph G is called 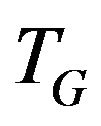 -compatible if
-compatible if 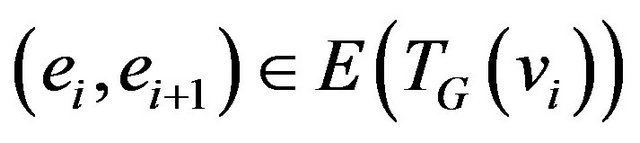 for each i
for each i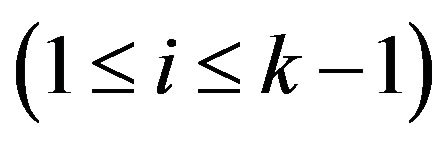 .
.
Theorem 1 [S. Szeider]. If all graphs of transitions belong either class M of full multipartite graphs or class P of matchings then the problem of 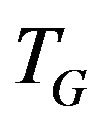 -compatible trail constructing can be solved by the time
-compatible trail constructing can be solved by the time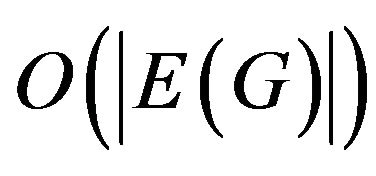 . Otherwise this problem is NP-complete.
. Otherwise this problem is NP-complete.
If the system of transitions for a vertex 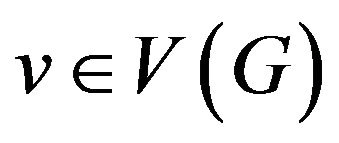 is a matching then this problem can be reduced to the problem for graph
is a matching then this problem can be reduced to the problem for graph
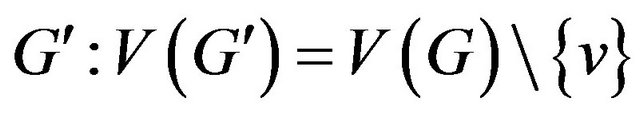 ,
,
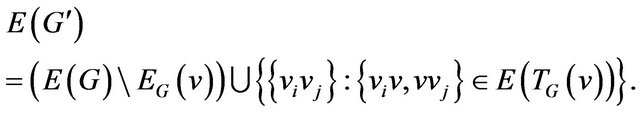
If for any vertex 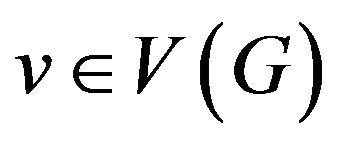 graph
graph 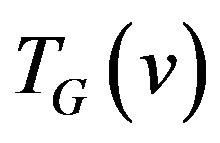 is full multipartite graph then a trail can be constructed by the following algorithm.
is full multipartite graph then a trail can be constructed by the following algorithm.
Algorithm 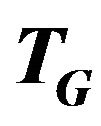 -Compatible Path
-Compatible Path
• Input:
• Graph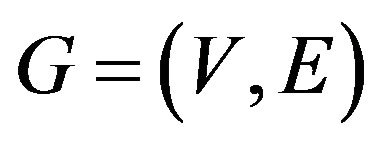 ;
;
• Vertices x, y the end-vertices of 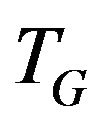 -compatible trail;
-compatible trail;
• System of transitions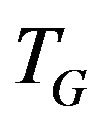 :
: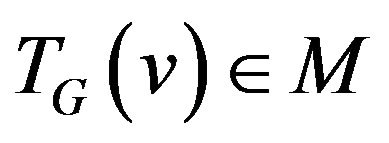
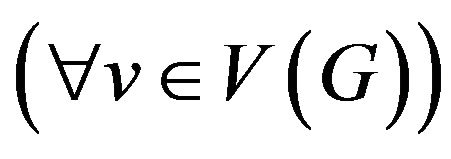 .
.
• Output:
• The sequence of edges corresponding to 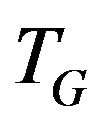 -compatible trail between vertices x and y or the message that such a path does not exist.
-compatible trail between vertices x and y or the message that such a path does not exist.
Step 1. If vertex x or vertex y is isolated then stop: path does not exist.
Step 2. Delete all isolated vertices from graph G.
Step 3. Construct the supplementary graph 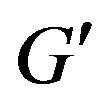 as following (figure 1):
as following (figure 1):
• Each vertex 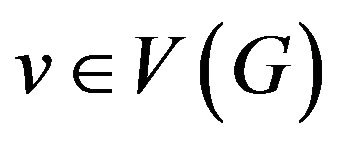 should be split into vertices
should be split into vertices 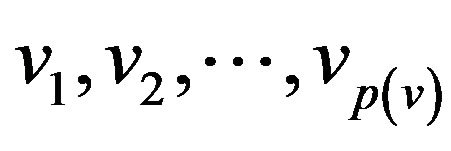 where
where 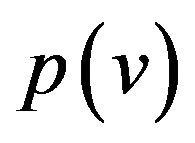 be the number of parts of graph
be the number of parts of graph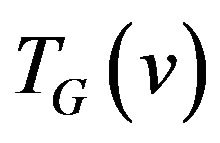 . The edges of corresponding part of graph
. The edges of corresponding part of graph 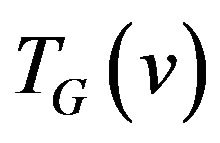 and one additional vertex
and one additional vertex 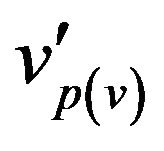 are incident to vertex
are incident to vertex ;
;
• Add two new vertices 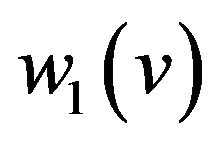 and
and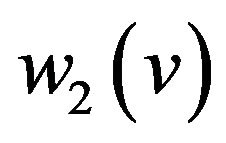 , edge
, edge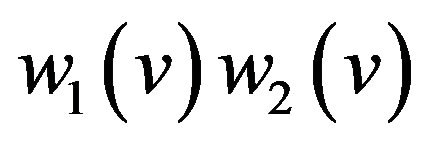 , and edge
, and edge 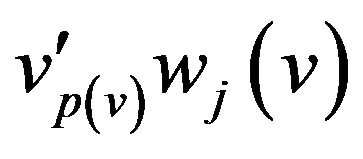 for each part of graph
for each part of graph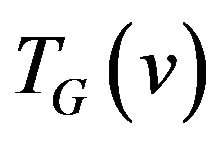 ,
,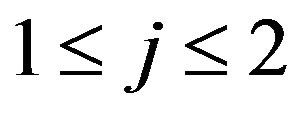 .
.
Step 4. Construct the initial matching for graph 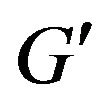
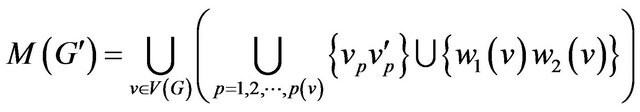 .
.
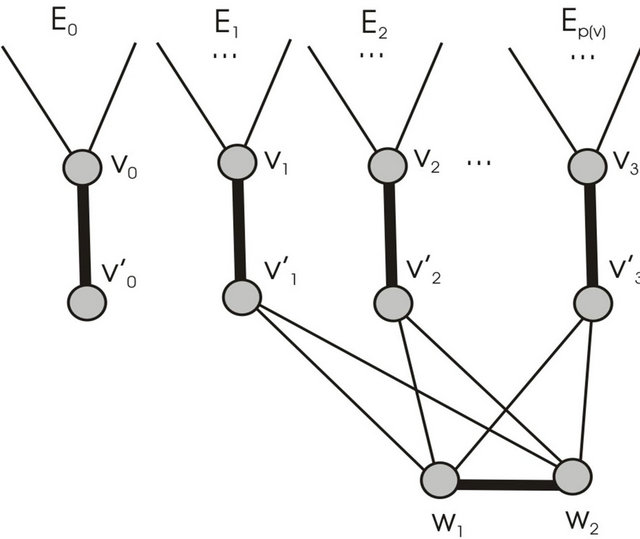
Figure 1. Illustration how supplementary graph 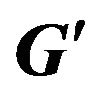 is constructed.
is constructed.
Step 5. Find the alternate sequence between vertices x and y that enlarges the cardinality of matching for graph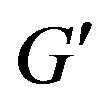 . If it’s impossible to find such a sequence then stop (matching
. If it’s impossible to find such a sequence then stop (matching 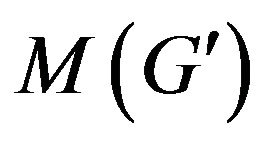 has maximal cardinality and graph has no
has maximal cardinality and graph has no 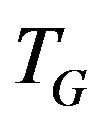 -compatible path). Otherwise all the edges of found enlarging path except of additional edges of graph
-compatible path). Otherwise all the edges of found enlarging path except of additional edges of graph 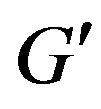 produce the
produce the 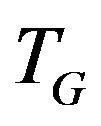 -compatible path between vertices x and y. Stop.
-compatible path between vertices x and y. Stop.
Let’s admit that there is open question in research [7]. This question is about recognition the multipartiteness of graphs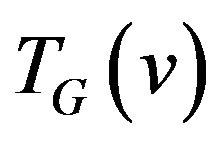 . Problems of constructing the allowed path or set of paths covering all the edges of given graph are not also considered.
. Problems of constructing the allowed path or set of paths covering all the edges of given graph are not also considered.
Let’s illustrate an example of graph G (figure 2) that algorithm 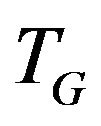 -COMPATIBLE PATH cannot be used for constructing of paths covering all edges of graph G. Let the following system of transitions
-COMPATIBLE PATH cannot be used for constructing of paths covering all edges of graph G. Let the following system of transitions 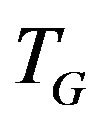 is defined for the graph:
is defined for the graph:
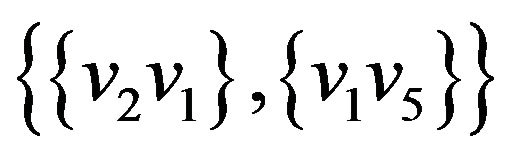 ,
, 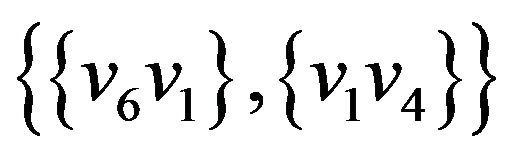 ,
, 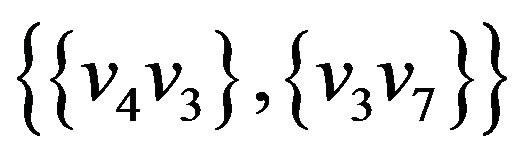 ,
, 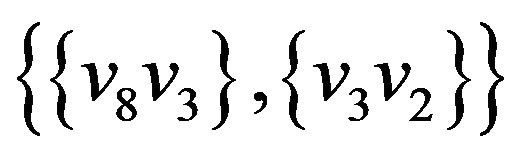 ,
, 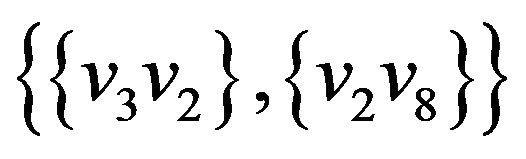 ,
, 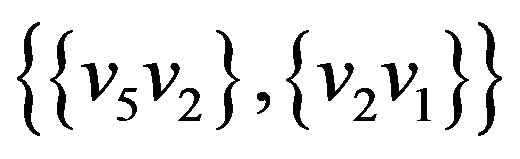 ,
, 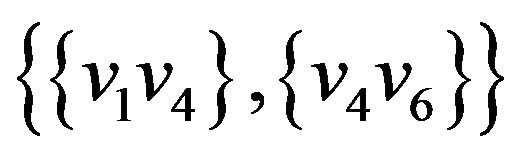 ,
, 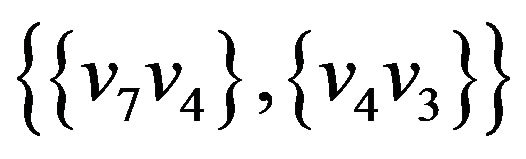 ,
, 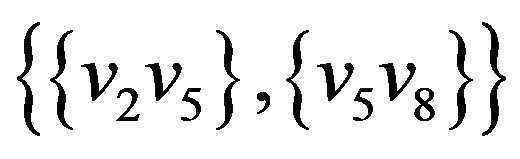 ,
, 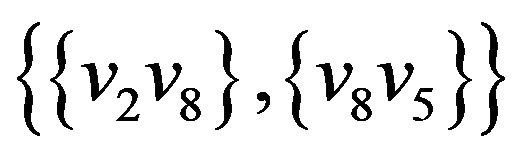 ,
, 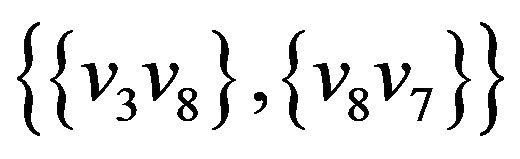 ,
, 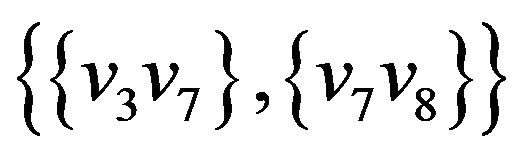 ,
, 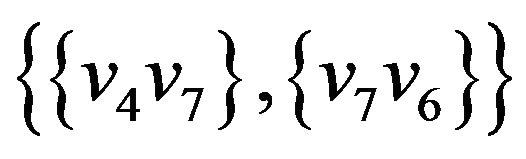 ,
, 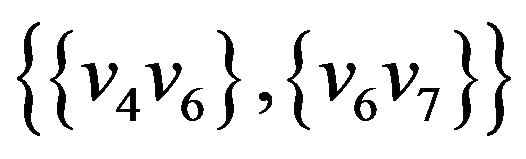 ,
, 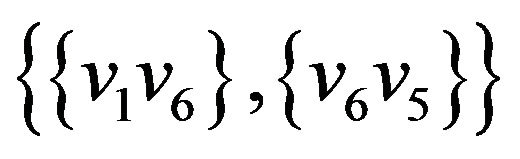 ,
,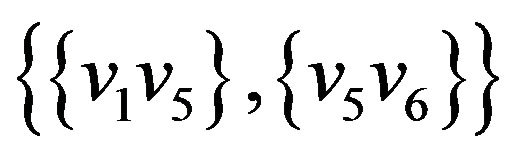 .
.
Supplementary graph  for finding of
for finding of 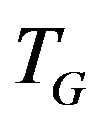 -compatible path between vertices
-compatible path between vertices 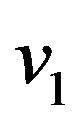 and
and 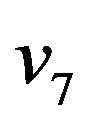 which construction is reviewed on step 3 of algorithm is shown at figure 3.
which construction is reviewed on step 3 of algorithm is shown at figure 3.
The initial matching 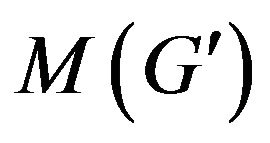 is marked by thick lines. The alternate enlarging sequence of edges for this matching be
is marked by thick lines. The alternate enlarging sequence of edges for this matching be
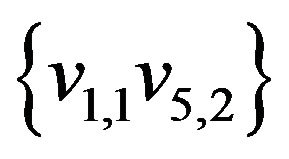 ,
, 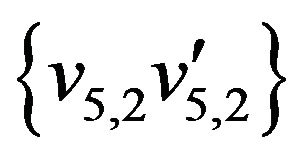 ,
,  ,
, 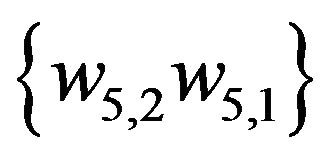 ,
, 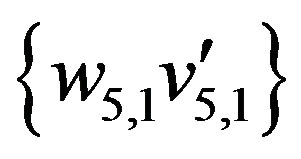 ,
, 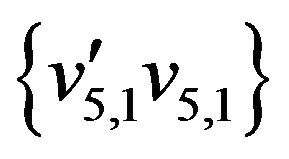 ,
, 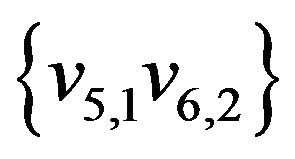 ,
, 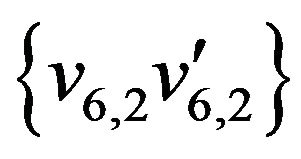 ,
,  ,
, 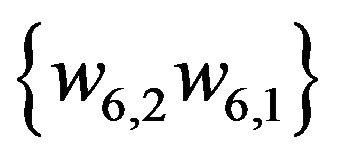 ,
, 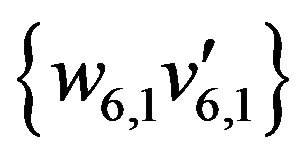 ,
, 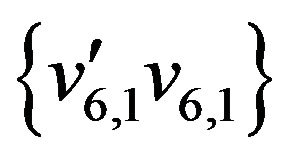 ,
,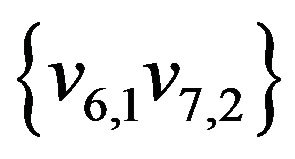 .
.
Edges of this sequence not belonging the initial matching are represented by dash line. These edges form the set
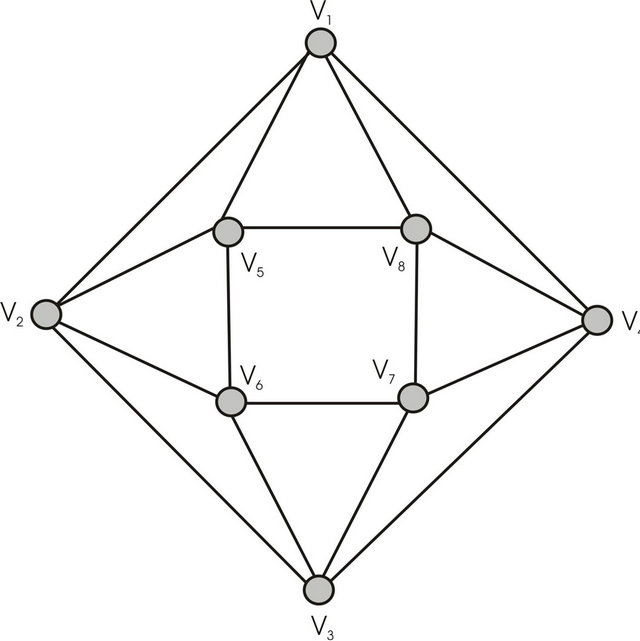
Figure 2. Example of graph.
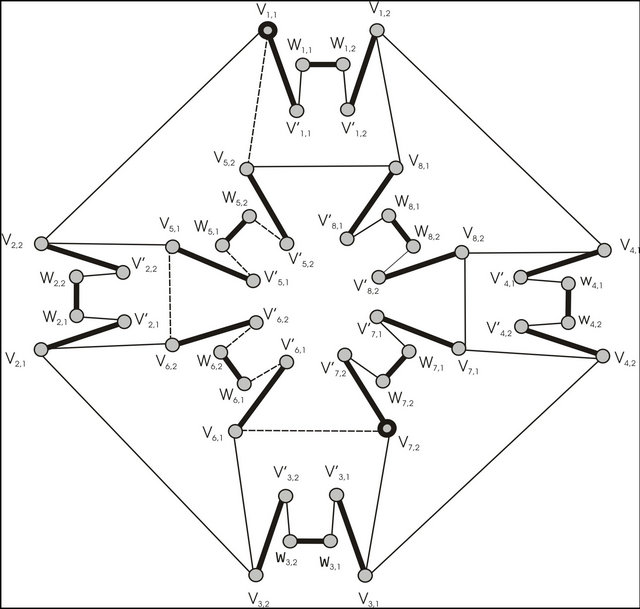
Figure 3. Graph G' received of graph G by additional constructions.
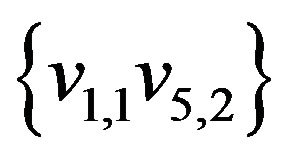 ,
, 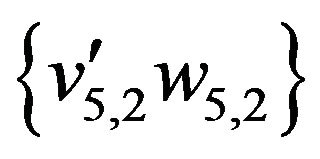 ,
, 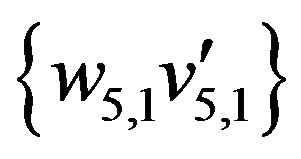 ,
, 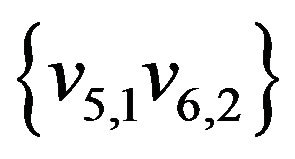 ,
, 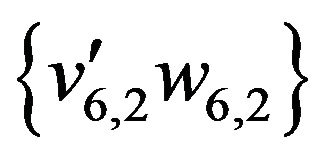 ,
, 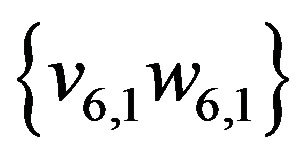 ,
,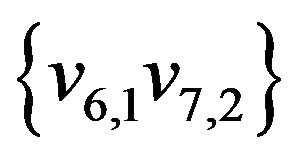 .
.
All edges of this set belonging to graph G i.e. ,
,  form
form 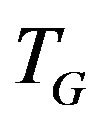 -compatible path from vertex
-compatible path from vertex 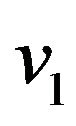 to vertex
to vertex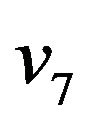 .
.
Using algorithm 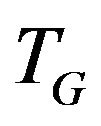 -COMPATIBLE PATH it’s possible to construct only a simple trail between two different vertices (i.e. a trail where each vertex is presented only once).
-COMPATIBLE PATH it’s possible to construct only a simple trail between two different vertices (i.e. a trail where each vertex is presented only once).
Figure 4 shows the software realization of the represented algorithm. The bold line marks the found trail between vertices 1 and 4. This trail corresponds the system
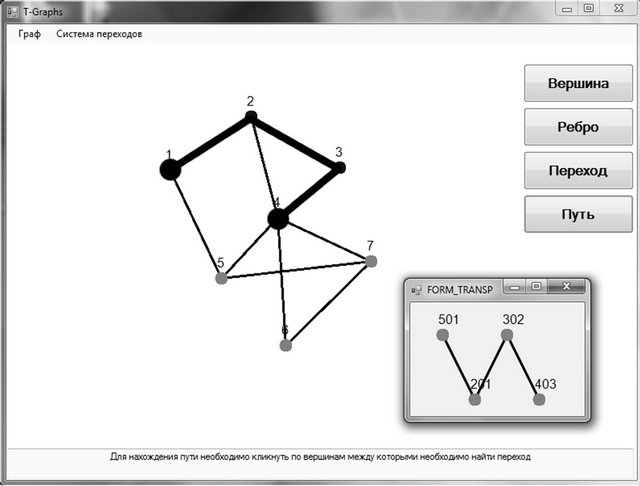
Figure 4. Software for compatible path algorithm.
of allowed transitions (see the additional window at right bottom side).
However in common the direct use of this algorithm does not allow to solve the problem of 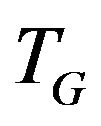 -compatible path with maximal number of edges constructing. Actually the matching of maximal cardinality for graph
-compatible path with maximal number of edges constructing. Actually the matching of maximal cardinality for graph 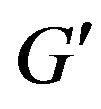 cannot contain the pairs of edges forming forbidden transition because these edges are incident to one common vertex of graph
cannot contain the pairs of edges forming forbidden transition because these edges are incident to one common vertex of graph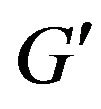 . At the same time, in common there may exist
. At the same time, in common there may exist 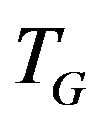 -compatible path containing such a pair of edges.
-compatible path containing such a pair of edges.
For example, for graph G presented on figure 2 the path
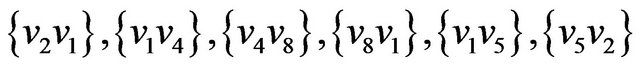
in principle cannot be received by constructing the matching of maximal weight for graph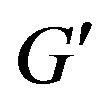 . This path begins from edge
. This path begins from edge 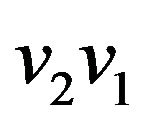 and ends by edge
and ends by edge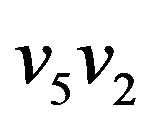 . These edges form forbidden transition
. These edges form forbidden transition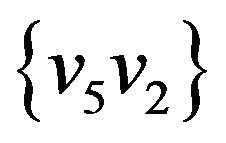 ,
, 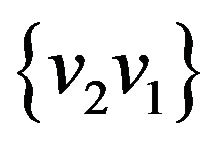 , consequently, graph
, consequently, graph 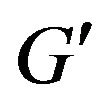 does not contain the alternate path with both of these edges.
does not contain the alternate path with both of these edges.
Thus, the question of multipartite 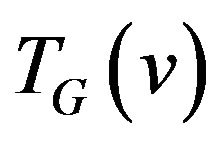 graph recognition is still open as well as the problem of allowed path constructing or finding the set of paths covering all the edges of initial graph G.
graph recognition is still open as well as the problem of allowed path constructing or finding the set of paths covering all the edges of initial graph G.
3. Algorithm for Constructing of Compatible Eulerian Trails
In the previous section the restrictions for paths were stated in the terms of allowed transitions system [7]. It’s shown that the problem of constructing the allowed path in graph G can be solved by polynomial time if a system of transitions 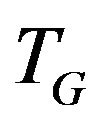 consists only of matchings and full multipartite graphs. It’s trivial to recognize if graph of allowed transitions belongs to the class of matchings. If we want recognize if transitions graph belongs to class of full multipartite graphs it’s expedient to use the definition of partition system [3-5,8].
consists only of matchings and full multipartite graphs. It’s trivial to recognize if graph of allowed transitions belongs to the class of matchings. If we want recognize if transitions graph belongs to class of full multipartite graphs it’s expedient to use the definition of partition system [3-5,8].
The conception of partition system is used for definition of allowed trail in terms of forbidden transitions.
Definition 4. Let 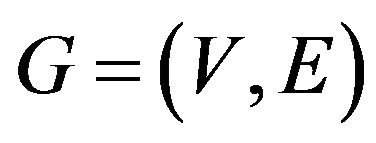 be a graph. Let
be a graph. Let 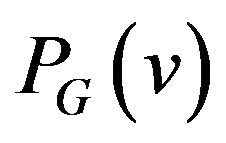 be some partition of set
be some partition of set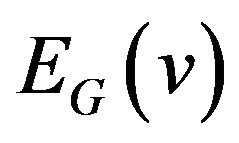 . Then the partition system of graph G be the system of sets
. Then the partition system of graph G be the system of sets 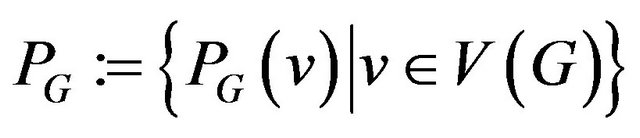 .
.
Definition 5. Let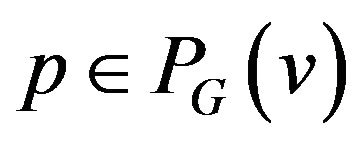 ,
,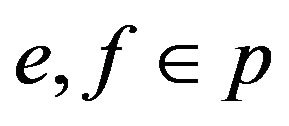 . A trail not containing the transitions
. A trail not containing the transitions 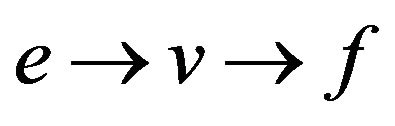 and
and 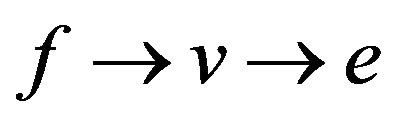 can be called
can be called  -compatible, and transitions
-compatible, and transitions 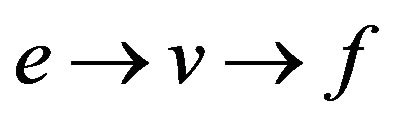 and
and 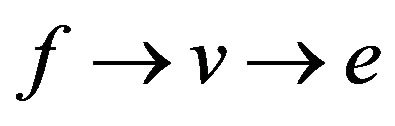 are forbidden.
are forbidden.
Let's admit that graph of allowed transitions 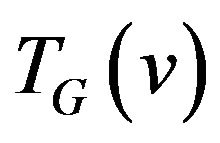 unambiguously defines the graph of forbidden transitions
unambiguously defines the graph of forbidden transitions 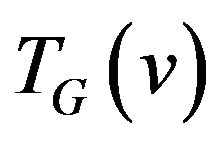 which is the complement of allowed transitions graph to full graph. Thus, using definitions 1-3 the problem either with use of allowed transitions or forbidden transitions can be stated.
which is the complement of allowed transitions graph to full graph. Thus, using definitions 1-3 the problem either with use of allowed transitions or forbidden transitions can be stated.
So the partition system is defined on the set of 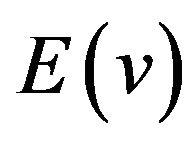 (the set of vertices incident to v). If edges
(the set of vertices incident to v). If edges 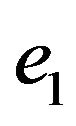 and
and 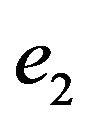 belong to one subset then edge
belong to one subset then edge 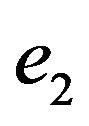 cannot be placed after the edge
cannot be placed after the edge 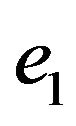 in a trail. Let graph
in a trail. Let graph 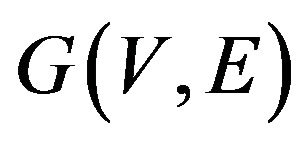 be defined by the adjacency list. Its elements are the structures. Each element of this structure consists of two fields: vertex number
be defined by the adjacency list. Its elements are the structures. Each element of this structure consists of two fields: vertex number 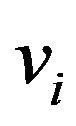 (this vertex is adjacent to the current one); the number of partition element
(this vertex is adjacent to the current one); the number of partition element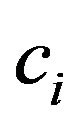 . To define the degree of the current vertex it is enough to count the number of elements of adjacency list.
. To define the degree of the current vertex it is enough to count the number of elements of adjacency list.
Let’s admit that each edge e belongs to two adjacency lists of vertices 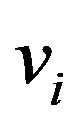 and
and 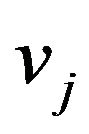 (the ends of an edge). But for each vertex edge e belongs to different partition systems.
(the ends of an edge). But for each vertex edge e belongs to different partition systems.
Input data are represented by the following list vector < list < pair
All data are represented by a vector of vertices, each element of this vector is a list of pairs. The first pair of each list is a vertex number, the second one is its degree. The other pairs represent the numbers of adjacent vertices and number of corresponding partition set.
On the other side, graph of allowed transitions defined by partition system 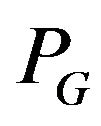 cannot be arbitrary, and belongs to class M of full multipartite graphs: the elements of partition
cannot be arbitrary, and belongs to class M of full multipartite graphs: the elements of partition 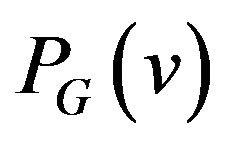 define the parts of graph
define the parts of graph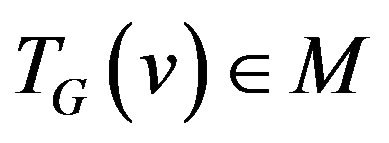 , and set of its edges
, and set of its edges
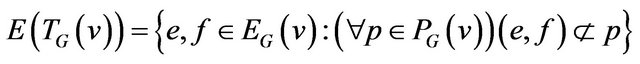 .s Graph of forbidden transitions
.s Graph of forbidden transitions 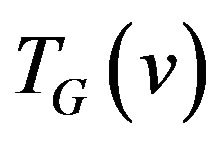 in this case will consist of
in this case will consist of 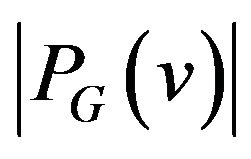 cliques, this fact can be used for recognition if
cliques, this fact can be used for recognition if 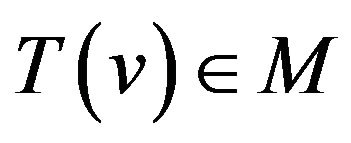 using algorithm [9].
using algorithm [9].
As it was considered earlier, algorithm of S. Szeider in common does not allow constructing of allowed trails having maximal length. The most interesting are allowed Eulerian trails. The necessary and sufficient condition for 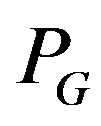 -compatible trails existence is proved by the following theorem [8].
-compatible trails existence is proved by the following theorem [8].
Theorem 2 [A. Kotzig]. Connected Eulerian graph G has 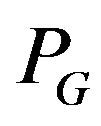 -compatible Eulerian trail if and only if
-compatible Eulerian trail if and only if
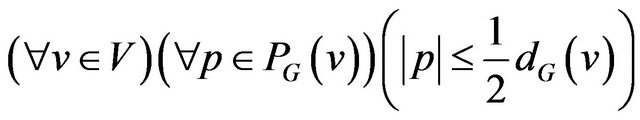 .
.
Obviously, complexity of checking the condition of existence of 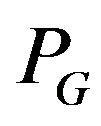 -compatible Eulerian trail is not more than
-compatible Eulerian trail is not more than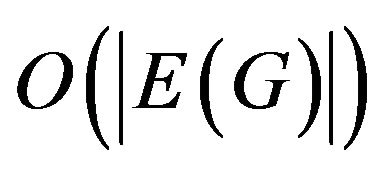 .
.
Let’s list the algorithm for construction of compatible trail.
Algorithm PG-Compatible Eulerian Trail
• Input data:
• Eulerian graph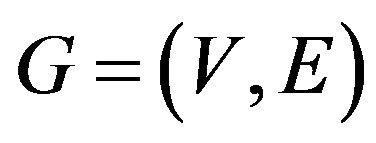 • Transitions system
• Transitions system 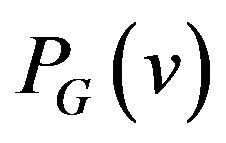
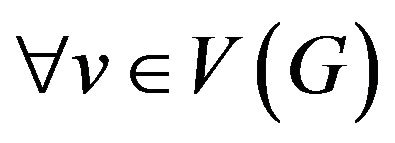 .
.
• Output data:
• Allowed Eulerian cycle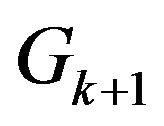 .
.
Step 1. Let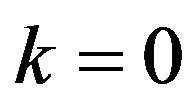 ,
,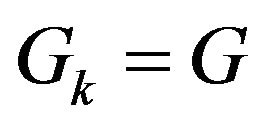 .
.
Step 2. Find a vertex v for which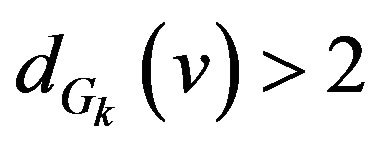 .
.
Step 3. Find element of partition system containing maximal number of edges. It’s enough to look through the adjacency list of current vertex v and count how many times each element of partition meets at this list. Choosing this element we get a class
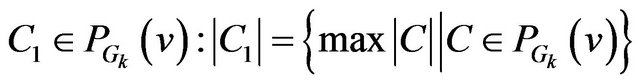 .
.
Step 4. Find any edges 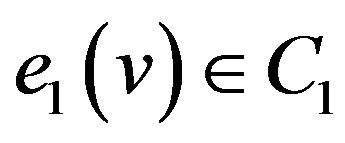 and
and 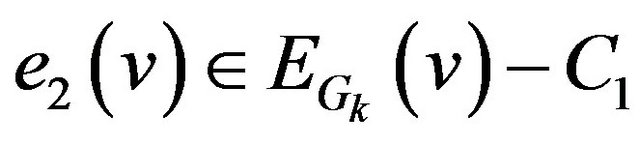 . If it’s possible choose edges
. If it’s possible choose edges 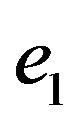 and
and 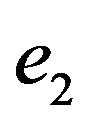 incident to vertices of degree more than 2. If set
incident to vertices of degree more than 2. If set  then stop: there is no
then stop: there is no 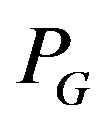 -compatible Eulerian trail. Otherwise go to step 5.
-compatible Eulerian trail. Otherwise go to step 5.
Step 5. Construct graph 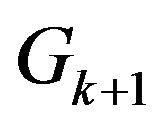 by detaching vertex
by detaching vertex , to which only edges
, to which only edges 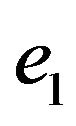 and
and 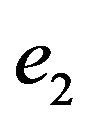 are incident, from vertex v. The other edges are kept incident to vertex v.
are incident, from vertex v. The other edges are kept incident to vertex v.
Step 6. Let class 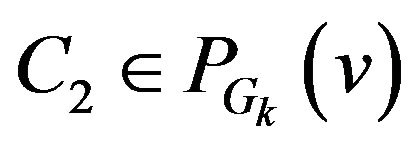 contains the edge
contains the edge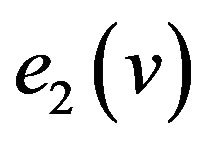 . Exclude vertices
. Exclude vertices  and
and 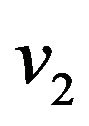 from partition system. Define
from partition system. Define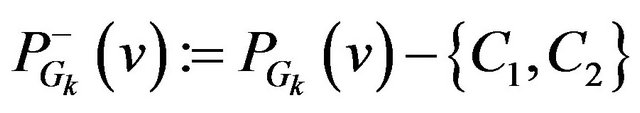 .
.
For further modification of partition system define the following.
Step 6.1. All partition systems not containing vertex v are taken to the modified system without any changes.
Step 6.2. If systems 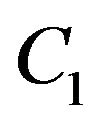 and
and 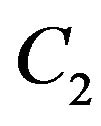 had been consisted of one edge
had been consisted of one edge 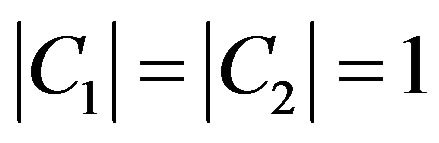 then
then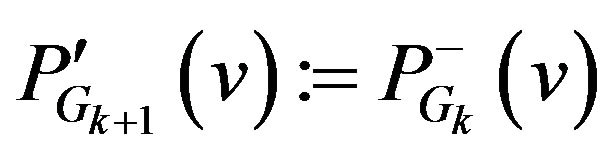 .
.
Step 6.3. If 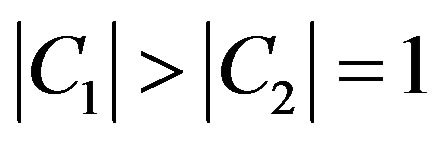 then
then
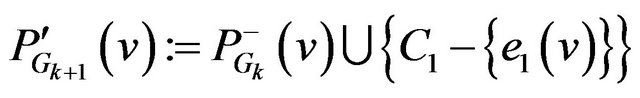 .
.
Step 6.4. If 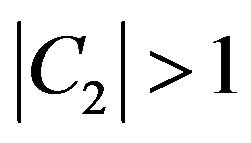 then
then
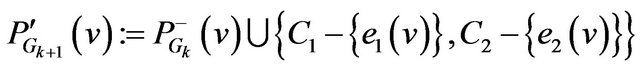 .
.
Step 6.5. Construct
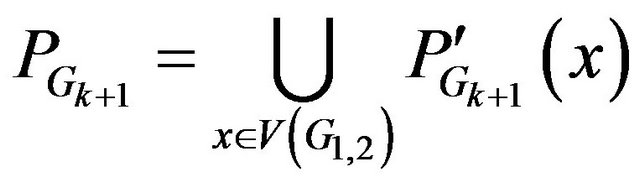 .
.
Step 7. Define the value
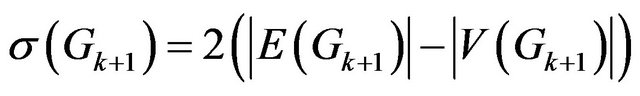 .
.
Let’s admit that the number of edges is a constant value and the number of vertices is increased by 1.
Step 8. If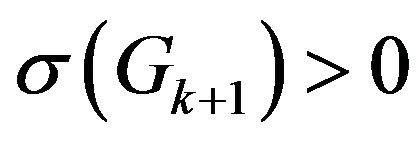 , let
, let 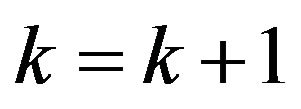 and go to step 2 for graph
and go to step 2 for graph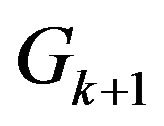 . Otherwise go to step 9.
. Otherwise go to step 9.
Step 9. Choose any vertex v and mark all achievable vertices. If there are unmarked vertices go to step 10 otherwise stop the received graph 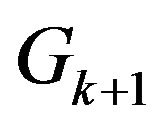 is Eulerian trail without forbidden transitions.
is Eulerian trail without forbidden transitions.
Step 10. Get vertices 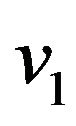 and
and 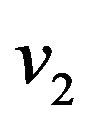 from a list of marked and unmarked vertices of graph
from a list of marked and unmarked vertices of graph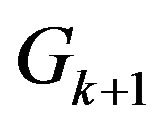 . These vertices are split from vertex v of graph
. These vertices are split from vertex v of graph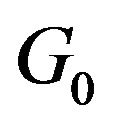 . Unite them to one vertex
. Unite them to one vertex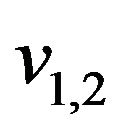 . There we get a modified graph
. There we get a modified graph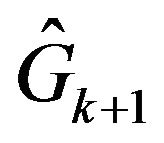 . Let
. Let .
.
Step 11. Choose edges  and
and
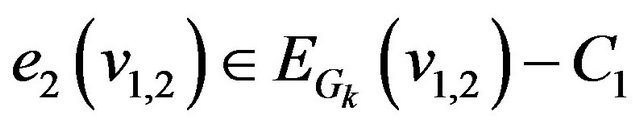 so that
so that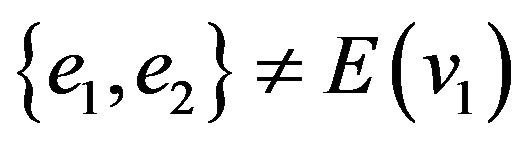 and
and
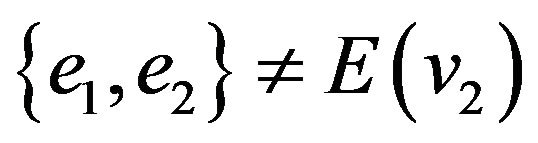 . If set
. If set 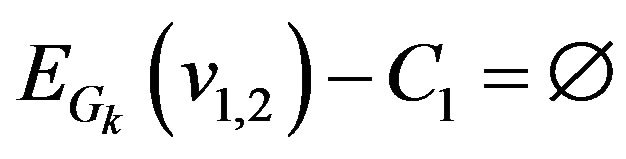 then stop: there is no
then stop: there is no 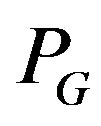 -compatible Eulerian trail. Otherwise construct graph
-compatible Eulerian trail. Otherwise construct graph 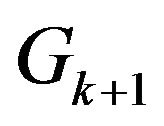 by splitting vertex
by splitting vertex 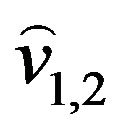 from vertex
from vertex 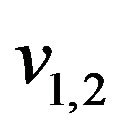 Only edges
Only edges 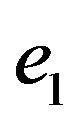 and
and 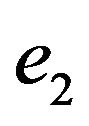 are incident to vertex
are incident to vertex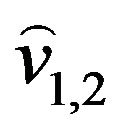 . All other edges are incident to vertex
. All other edges are incident to vertex 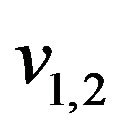 and go to step 9.
and go to step 9.
The following theorem is proved in [9].
Theorem 3. Algorithm 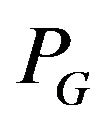 -compatible Eulerian trail correctly solves the problem of constructing the
-compatible Eulerian trail correctly solves the problem of constructing the 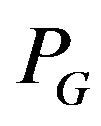 - compatible Eulerian trail.
- compatible Eulerian trail.
That paper also shows that computing complexity of this algorithm is
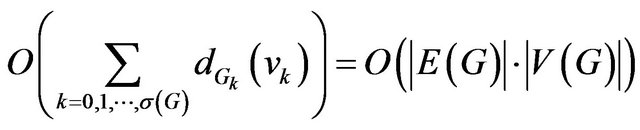 .
.
Thus, the constructed algorithms are resolved by the polynomial time and can be simply realized using standard computing facilities.
Let’s consider the allowed trail construction for a graph on figure 5. Let its transitions system is as shown in a table below. The numbers in white circles show the number of partition system the edge belongs for each vertex.
Let’s construct allowed Eulerian cycle beginning and ending at vertex 1. At the first iteration the first vertex is split. To simplify the illustration let’s consider the “short version” of vertex splitting (the example of “full version” is presented on figure 3). Figure 6 and table show graph with split vertex 1 and a list of connectivity where
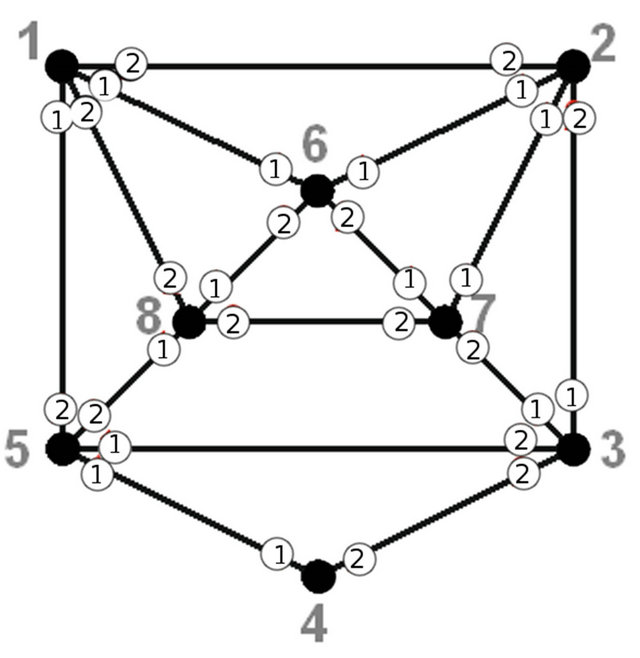
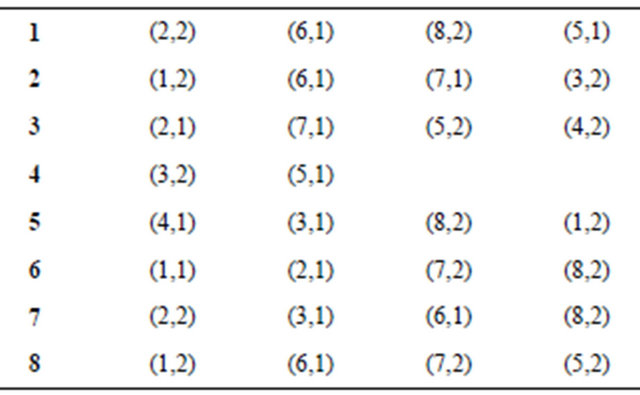
Figure 5. Example.
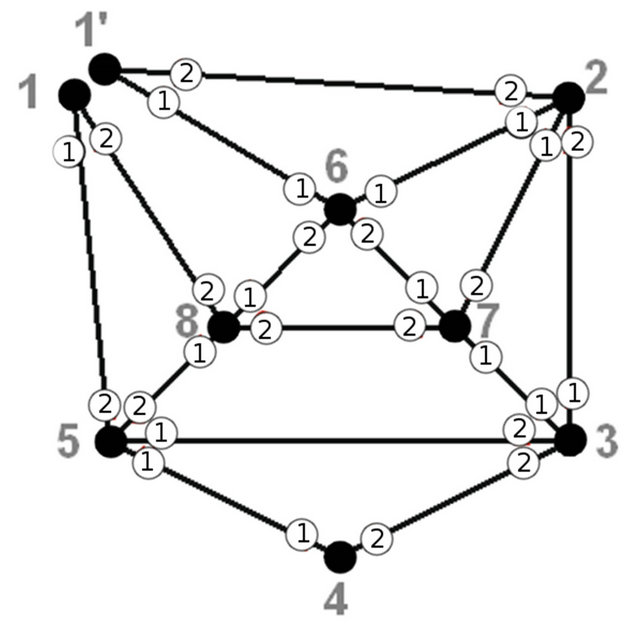
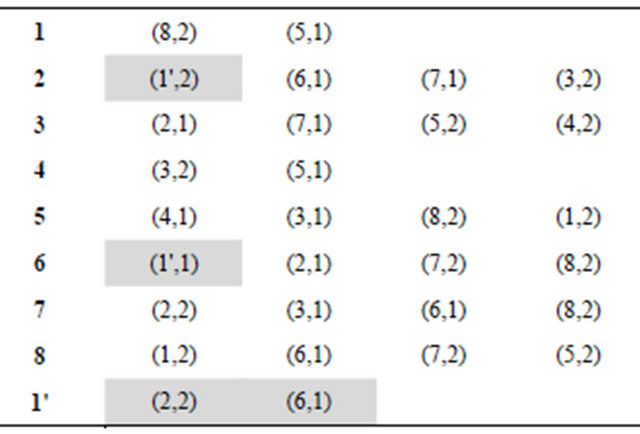
Figure 6. The first iteration of algorithm.
new or modified elements are colored by gray.
Figures 7-12 and tables under them represent all other iterations of algorithm.
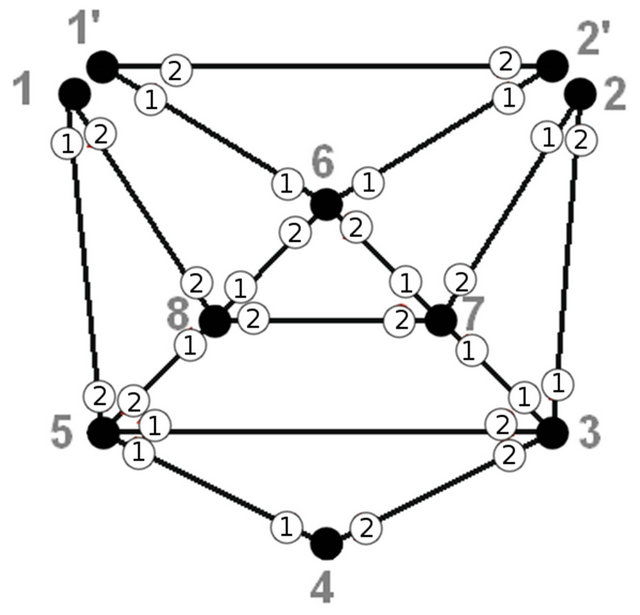
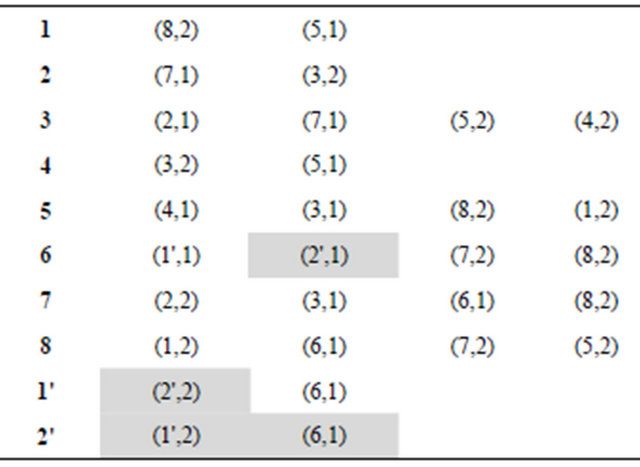
Figure 7. The second iteration of algorithm.
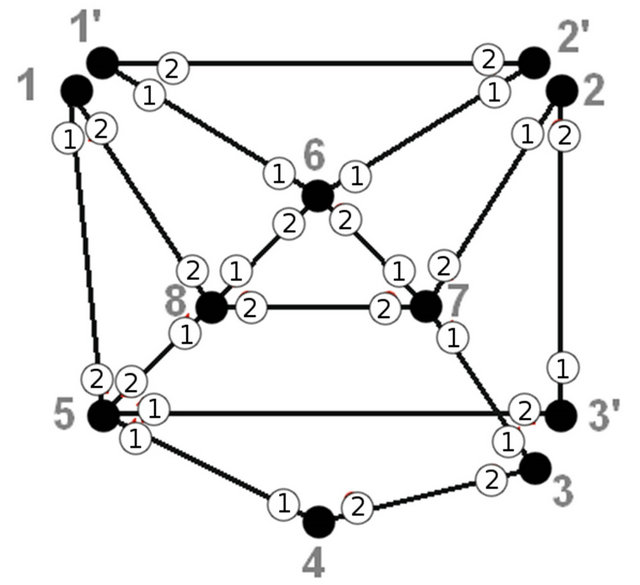
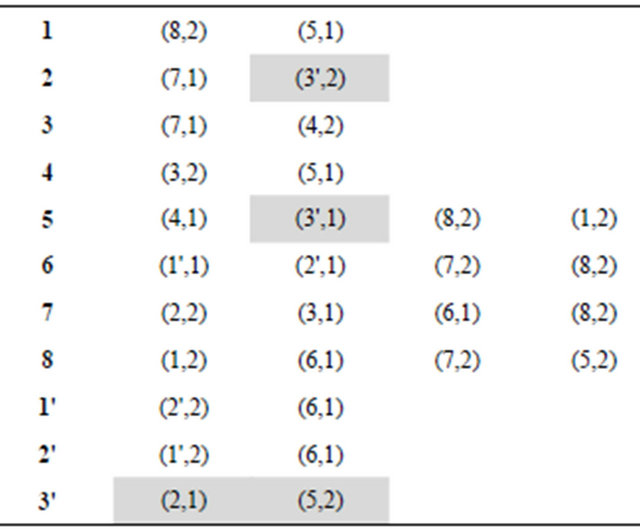
Figure 8. The third iteration of algorithm.
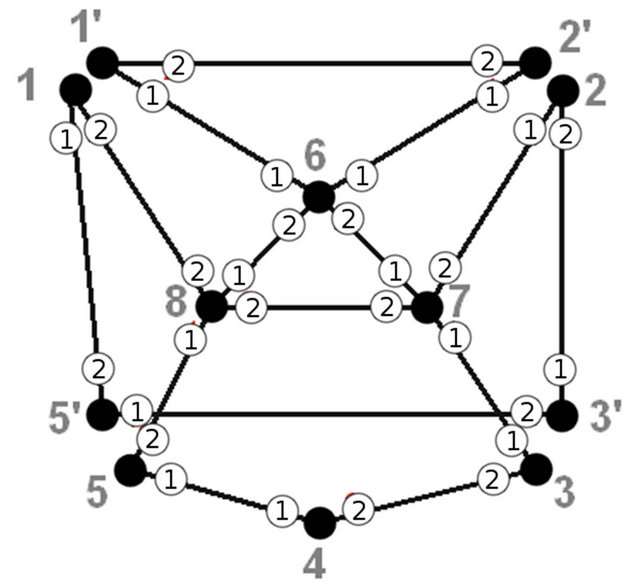

Figure 9. The forth iteration of algorithm.
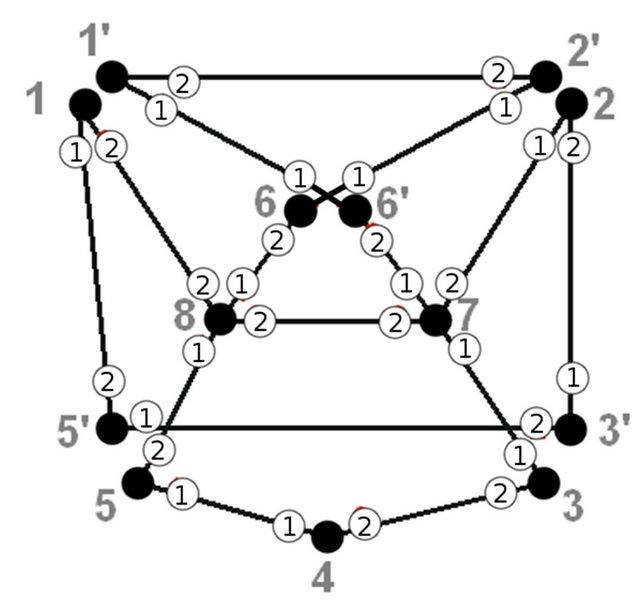
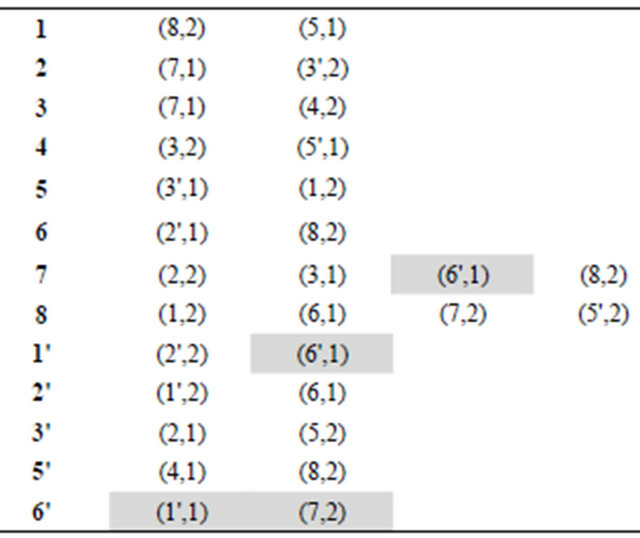
Figure 10. The fifth iteration of algorithm.
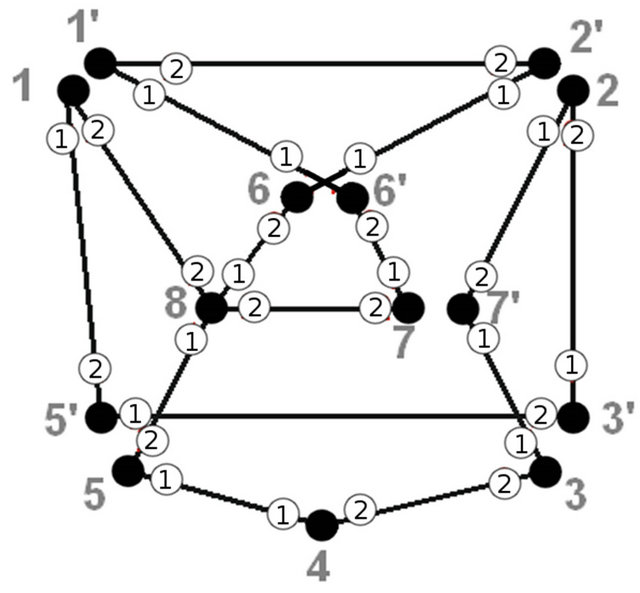
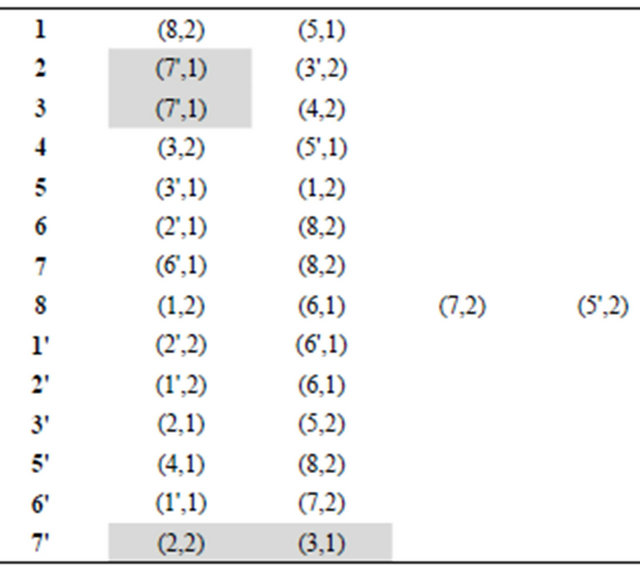
Figure 11. The sixth iteration of algorithm.
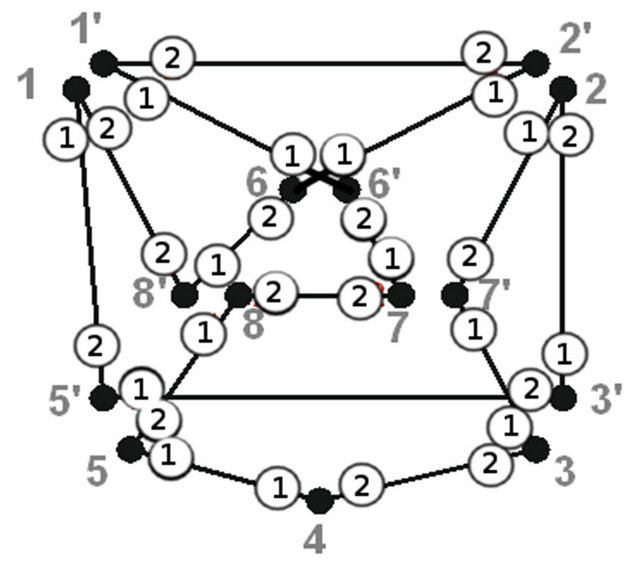

Figure 12. The last iteration of algorithm.
In result graph is split into a simple cycle. It’s possible to construct allowed Eulerian cycle beginning at any its vertex. For example, the following cycle beginning at vertex 1 can be constructed:
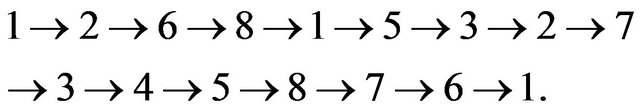
It’s possible to recognize the system of transitions and to solve the problem of constructing the allowable path by linear time. It’s also possible to find 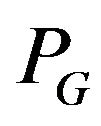 -allowable Eulerian cycle for Eulerian graph
-allowable Eulerian cycle for Eulerian graph 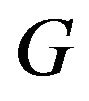 or to proclaim that such a cycle does not exist. This problem can be solved by the time
or to proclaim that such a cycle does not exist. This problem can be solved by the time 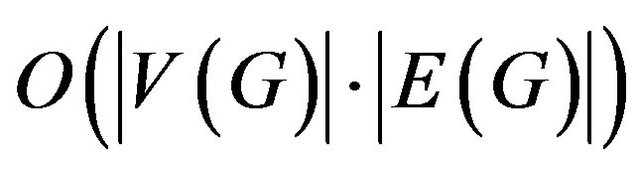 using algorithm
using algorithm 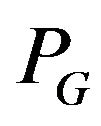 - compatible Eulerian trail.
- compatible Eulerian trail.
4. Acknowledgements
The research is supported by the Ministry of Education and Science of Russian Federation, contract 14.B37.21. 0395.
REFERENCES
- T. Panyukova, “Cover with Ordered Enclosing for Flat Graphs,” Electronic Notes in Discrete Mathematics, Vol. 28, 2007, pp. 17-24. doi:10.1016/j.endm.2007.01.004
- T. Pisanski, T. W. Tucker and A. Zitnik, “Straight-Ahead walks in Eulerian Graphs,” Discrete Mathematics, Vol. 281, No. 1-3, 2004, pp. 237-246. doi:10.1016/j.disc.2003.09.011
- H. Fleischner, “Eulerian Graphs and Related Topics,” Part 1, Vol. 1, Elsevier, Amsterdam, 1990.
- H. Fleischner, “Eulerian Graphs and Related Topics,” Part 1, Vol. 2, Elsevier, Amsterdam, 1991.
- H. Fleischner, L. W. Beineke and R. J. Wilson, “Eulerian Graphs, Selected Topics in Graph Theory 2,” Academic Press, London, New York, 1983, pp. 17-53.
- D. Chebikin, “On k-Edge-Ordered Graphs,” Discrete Mathematics, Vol. 281, No. 1-3, 2004, pp. 115-128. doi:10.1016/j.disc.2003.09.004
- S. Szeider, “Finding Paths in Graphs Avoiding Forbidden Transitions,” Discrete Applied Mathematics, Vol. 126, No. 2-3, 2003, pp. 261-273. doi:10.1016/S0166-218X(02)00251-2
- A. Kotzig, “Moves without Forbidden Transitions in a Graph,” Matematický Časopis, Vol. 18, No. 1, 1968, pp. 76-80.
- T. A. Panyukova, “The Paths with Local Restrictions,” Reports of South Ural State University. Section: Mathematical Modelling and Programming, Vol. 5, No. 16, 2010, pp. 58-67 (in Russian).

