Open Journal of Discrete Mathematics
Vol.2 No.3(2012), Article ID:21137,3 pages DOI:10.4236/ojdm.2012.23017
The Middle Equitable Dominating Graphs
1Department of Studies in Mathematics, University of Mysore, Mysore, India
2Department of Mathematics, King Abdulaziz University, Jeddah, KSA
Email: aalkenani10@hotmail.com
Received April 20, 2012; revised May 25, 2012; accepted June 15, 2012
Keywords: Eqitable Domination Number; Middle Equitable Dominating Graph; Intersection Graphs
ABSTRACT
Let 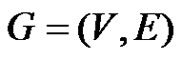 be a graph and A(G) is the collection of all minimal equitable dominating set of G. The middle equitable dominating graph of G is the graph denoted by Med(G) with vertex set the disjoint union of
be a graph and A(G) is the collection of all minimal equitable dominating set of G. The middle equitable dominating graph of G is the graph denoted by Med(G) with vertex set the disjoint union of 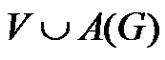 and (u, v) is an edge if and only if
and (u, v) is an edge if and only if 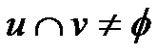 whenever
whenever 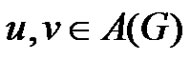 or
or 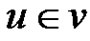 whenever
whenever 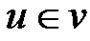 and
and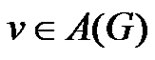 . In this paper, characterizations are given for graphs whose middle equitable dominating graph is connected and
. In this paper, characterizations are given for graphs whose middle equitable dominating graph is connected and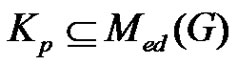 . Other properties of middle equitable dominating graphs are also obtained.
. Other properties of middle equitable dominating graphs are also obtained.
1. Introduction
All the graphs considered here are finite and undirected with no loops and multiple edges. As usual 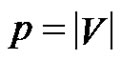 and
and 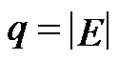 denote the number of vertices and edges of a graph
denote the number of vertices and edges of a graph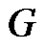 , respectively. In general, we use
, respectively. In general, we use 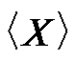 to denote the subgraph induced by the set of vertices
to denote the subgraph induced by the set of vertices  and
and 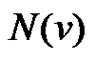 and
and 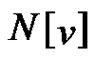 denote the open and closed neighbourhoods of a vertex v, respectively. A set D of vertices in a graph G is a dominating set if every vertex in
denote the open and closed neighbourhoods of a vertex v, respectively. A set D of vertices in a graph G is a dominating set if every vertex in 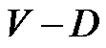 is adjacent to some vertex in D. The domination number
is adjacent to some vertex in D. The domination number 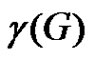 is the minimum cardinality of a dominating set of
is the minimum cardinality of a dominating set of . For terminology and notations not specifically defined here we refer reader to [1]. For more details about parameters of domination number, we refer to [2], and [3].
. For terminology and notations not specifically defined here we refer reader to [1]. For more details about parameters of domination number, we refer to [2], and [3].
A subset D of 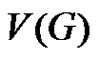 is called an equitable dominating set of a graph
is called an equitable dominating set of a graph 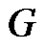 if for every
if for every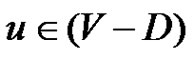 , there exists a vertex
, there exists a vertex  such that
such that 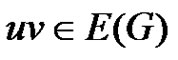 and
and 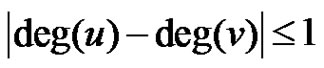 . The minimum cardinality of such a dominating set is denoted by
. The minimum cardinality of such a dominating set is denoted by 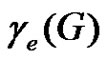 and is called equitable domination number of
and is called equitable domination number of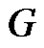 .
.  is minimal if for any vertex
is minimal if for any vertex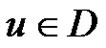 ,
, 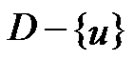 is not a equitable dominating set of
is not a equitable dominating set of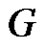 . A subset
. A subset 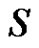 of
of  is called a equitable independent set, if for any
is called a equitable independent set, if for any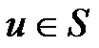 ,
, 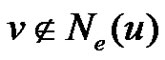 , for all
, for all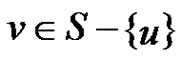 . If a vertex
. If a vertex 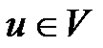 be such that
be such that  for all
for all 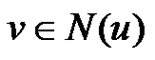 then
then 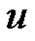 is in each equitable dominating set. Such vertices are called equitable isolates. The equitable neighbourhood of
is in each equitable dominating set. Such vertices are called equitable isolates. The equitable neighbourhood of  denoted by
denoted by 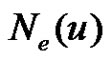 is defined as
is defined as 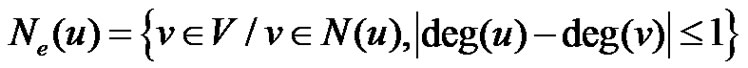 and
and 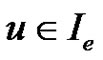

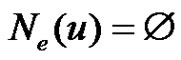 . The cardinality of
. The cardinality of  is denoted by
is denoted by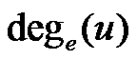 . The maximum and minimum equitable degree of a point in G are denoted respectively by
. The maximum and minimum equitable degree of a point in G are denoted respectively by 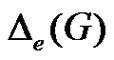 and
and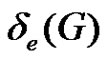 . That is
. That is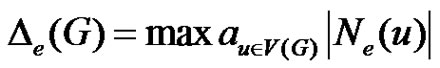 ,
,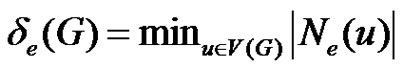 . An edge
. An edge 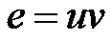 called equitable edge if
called equitable edge if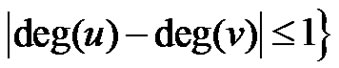 , for more details about equitable domination number see [4]. Let
, for more details about equitable domination number see [4]. Let 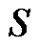 be a finite set and let
be a finite set and let 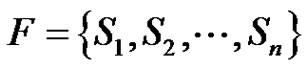 be a partition of
be a partition of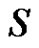 . Then the intersection graph
. Then the intersection graph 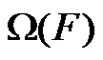 of
of 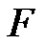 is the graph whose vertices are the subsets in
is the graph whose vertices are the subsets in 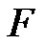 and in which two vertices
and in which two vertices 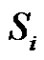 and
and 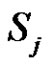 are adjacent if and only if
are adjacent if and only if 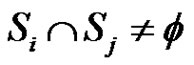 ,
, . Kulli and Janakiram introduced new classes of intersection graphs in the field of domination theory see [5-8].
. Kulli and Janakiram introduced new classes of intersection graphs in the field of domination theory see [5-8].
The purpose of this paper is to introduce a new class of intersection graphs in the field of domination theory as follows:
Let 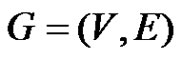 be a graph and
be a graph and 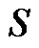 be the collection of minimal equitable dominating set of
be the collection of minimal equitable dominating set of . The middle equitable dominating graph of
. The middle equitable dominating graph of 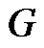 is the graph denoted by
is the graph denoted by 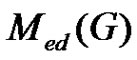 with vertex set the disjoint union
with vertex set the disjoint union 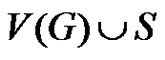 and
and 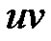 is an edge if and only if
is an edge if and only if 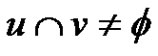 whenever
whenever 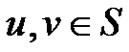 or
or 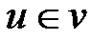 whenever
whenever 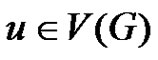 and
and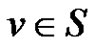 .
.
Example. Let G be a graph as in Figure 1(a), then the equitable dominating sets are 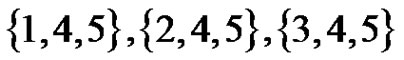 and the The middle equitable dominating graph shown in Figure 1(b).
and the The middle equitable dominating graph shown in Figure 1(b).
2. Main Results
Theorem 2.1. A graph 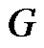 with
with 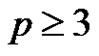 vertices is without equitable edge (equitable edge-free graph) if and only
vertices is without equitable edge (equitable edge-free graph) if and only
 (a) (b)
(a) (b)
Figure 1. Example.
if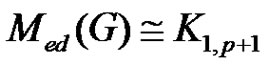 .
.
Proof. Suppose that 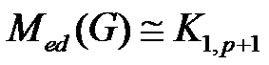 and if its possible that
and if its possible that 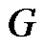 has equitable edge
has equitable edge . Then
. Then 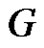 has at least two minimal equitable dominating set
has at least two minimal equitable dominating set , a contradiction.
, a contradiction.
Conversely, assume that 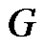 is equitable edge-free graph with p vertices. Then clear all the vertices are equitable isolated vertices, that is there is only one minimal equitable dominating set contains all the vertices and according the definition of
is equitable edge-free graph with p vertices. Then clear all the vertices are equitable isolated vertices, that is there is only one minimal equitable dominating set contains all the vertices and according the definition of , we get
, we get 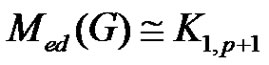 .
.
Corollary 2.2. If 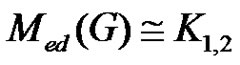 if and only if
if and only if 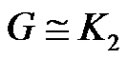 .
.
Corollary 2.3. If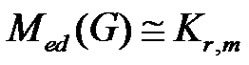 , where
, where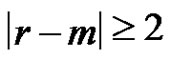 , then
, then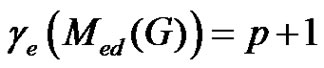 .
.
Corollary 2.4. Let G be complete multi bipartite graph
 , where
, where , where
, where , then
, then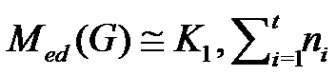 .
.
Proposition 2.5. 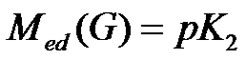 if and only if
if and only if  .
.
Proof. Suppose that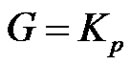 . Then clearly each vertex in
. Then clearly each vertex in 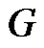 will form a minimal equitable dominating set. Hence
will form a minimal equitable dominating set. Hence .
.
Conversely, suppose 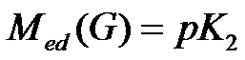 and
and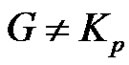 . Then there exists at least one minimal equitable dominating set
. Then there exists at least one minimal equitable dominating set  containing two vertices of
containing two vertices of . Then
. Then 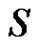 will form
will form 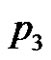 in
in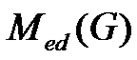 .
.
Proposition 2.6. If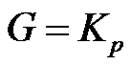 , then
, then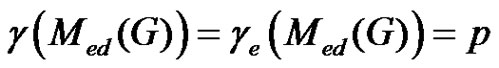 .
.
Proof. The proof coming directly from Proposition 2.5.
Theorem 2.7. Let 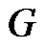 be a graph with p vertices and
be a graph with p vertices and 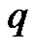 edges.
edges. 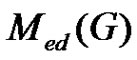 is a graph with
is a graph with 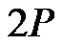 vertices and p edges if and only if
vertices and p edges if and only if .
.
Proof. If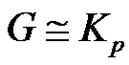 , then that is clear the
, then that is clear the 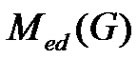 is a graph with
is a graph with 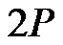 vertices and p edges.
vertices and p edges.
Conversely, let 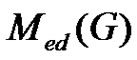 be
be 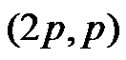 -graph. Since only the graph
-graph. Since only the graph 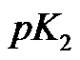 is of 2p vertices and p edges, then by Proposition 2.5
is of 2p vertices and p edges, then by Proposition 2.5 .
.
Theorem 2.8. Let 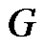 be a graph with p vertices and
be a graph with p vertices and 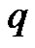 edges.
edges. 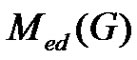 is a graph with
is a graph with 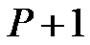 vertices and
vertices and 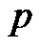 edges if and only if
edges if and only if 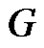 is equitable edge-free graph.
is equitable edge-free graph.
Proof. Let 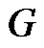 be equitable edge-free graph. Then by Theorem 2.1
be equitable edge-free graph. Then by Theorem 2.1 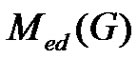 is a graph with
is a graph with 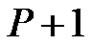 vertices and
vertices and 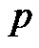 edges.
edges.
Conversely, let 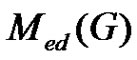 be a graph with
be a graph with 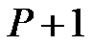 vertices and
vertices and 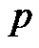 edges that means
edges that means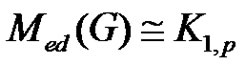 , and by Theorem 2.1
, and by Theorem 2.1 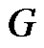 is equitable edge-free graph.
is equitable edge-free graph.
Theorem 2.9. [1] Let G be a graph, if D is maximal equitable independent set of G, then D also minimal equitable set.
Theorem 2.10. For any graph G with at least two vertices 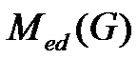 is connected if and only if
is connected if and only if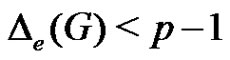 .
.
Proof. Let  and
and  be any two vertices if there is minimal equitable dominating set
be any two vertices if there is minimal equitable dominating set  containing u and v, the
containing u and v, the  are connected by the path
are connected by the path , and if there is no minimal equitable dominating containing both u and v. Then there exists a vertex
, and if there is no minimal equitable dominating containing both u and v. Then there exists a vertex 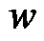 in
in 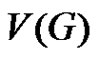 such that
such that 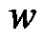 is neither adjacent to u nor v. Let D and D, be two maximal equitable independent set containing u, w and v, w respectively since every maximal equitable independent set is minimal equitable dominating set by Theorem 2.9, u and v are connected by the path
is neither adjacent to u nor v. Let D and D, be two maximal equitable independent set containing u, w and v, w respectively since every maximal equitable independent set is minimal equitable dominating set by Theorem 2.9, u and v are connected by the path . Thus
. Thus 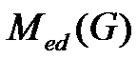 is connected. Hence
is connected. Hence 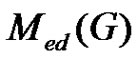 is connected.
is connected.
Conversely, suppose 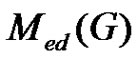 is connected. let
is connected. let 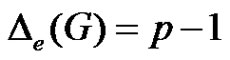 and let u be a vertex such that
and let u be a vertex such that 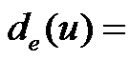
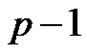 . Then
. Then 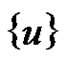 is minimal equitable dominating set and
is minimal equitable dominating set and  has at least two vertices , it is clear that
has at least two vertices , it is clear that 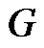 has no equitable isolated vertices, then
has no equitable isolated vertices, then 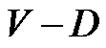 containing minimal equitable dominating set say
containing minimal equitable dominating set say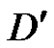 . Since
. Since 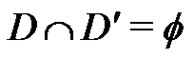 in
in  there is no path joining
there is no path joining 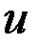 to any vertex of
to any vertex of , this implies that
, this implies that 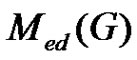 is disconnected, a contradiction. Hence
is disconnected, a contradiction. Hence .
.
Corollary 2.11. Let 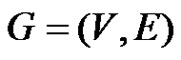 be a graph and
be a graph and 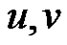 any two vertices in
any two vertices in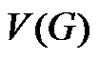 . Then
. Then , where
, where 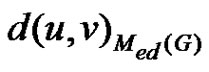 is the distance between the vertex
is the distance between the vertex and
and  in the graph
in the graph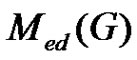 .
.
Theorem 2.12. For any graph ,
, 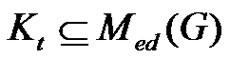 if and only if
if and only if  contains one equitable isolated vertex, where
contains one equitable isolated vertex, where  is the number of minimal equitable dominating set in
is the number of minimal equitable dominating set in .
.
Proof. If  has equitable isolated vertex then the subgraph of
has equitable isolated vertex then the subgraph of 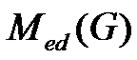 which induced by the set of all minimal equitable dominating sets of
which induced by the set of all minimal equitable dominating sets of 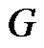 is complete graph
is complete graph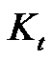 . Hence
. Hence .
.
Conversely, Suppose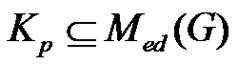 , then it is clear that the vertices of
, then it is clear that the vertices of  are the minimal equitable dominating sets of
are the minimal equitable dominating sets of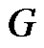 . Therefor there exists at least one equitable isolated vertex in
. Therefor there exists at least one equitable isolated vertex in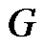 .
.
Theorem 2.13. For any graph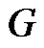 ,
, 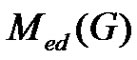 is either connected or it has at least one component which is
is either connected or it has at least one component which is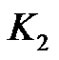 .
.
Proof. If , then by Theorem 2.10
, then by Theorem 2.10 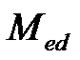 is connected, and By Proposition 2.5, if
is connected, and By Proposition 2.5, if 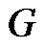 is complete
is complete 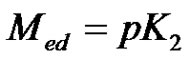 which is connected. Hence we must prove the case
which is connected. Hence we must prove the case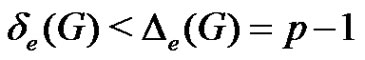 .
.
Let  be the set of vertices in
be the set of vertices in 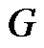 such that
such that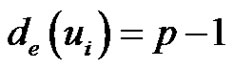 , where
, where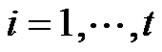 , then it is clear
, then it is clear 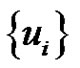 is minimal equitable dominating set. Then each vertex
is minimal equitable dominating set. Then each vertex 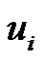 with the minimal equitable dominating set
with the minimal equitable dominating set 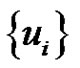
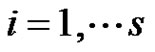 form component isomorphic to
form component isomorphic to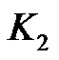 . Hence it has at least one component which is
. Hence it has at least one component which is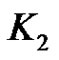 .
.
Theorem 2.14. For any graph 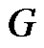 with
with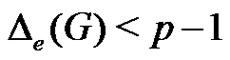 ,
,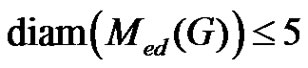 .
.
Proof. Let 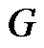 be any graph and
be any graph and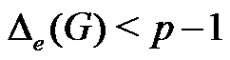 . Then by Theorem 2.10,
. Then by Theorem 2.10, 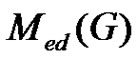 is connected, suppose
is connected, suppose 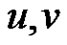 be any two vertices in
be any two vertices in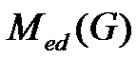 , then we have the following cases:
, then we have the following cases:
Case 1: Let  be any two vertices in
be any two vertices in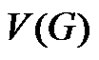 . Then by corollary 2.11,
. Then by corollary 2.11,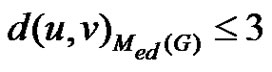 .
.
Case 2: Suppose 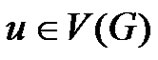 and
and 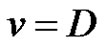 be a minimal equitable dominating set in
be a minimal equitable dominating set in , If
, If 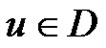 then
then 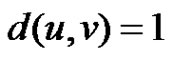 and if
and if 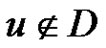 then there exists a vertex
then there exists a vertex  adjacent to
adjacent to . Hence
. Hence
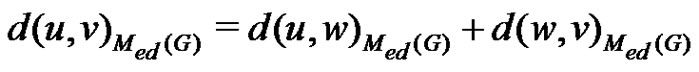 and from corollary 2.11 we have
and from corollary 2.11 we have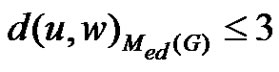 . Hence
. Hence 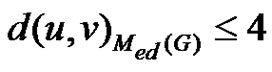 .
.
Case 3: Suppose that both u and 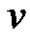 are not in
are not in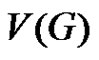 , and u = D,
, and u = D, 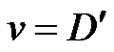 are two minimal equitable dominating sets if D and
are two minimal equitable dominating sets if D and  are adjacent, then
are adjacent, then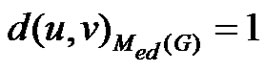 suppose that
suppose that 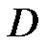 and
and 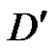 are not adjacent then every vertex
are not adjacent then every vertex 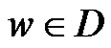 is adjacent to some vertex
is adjacent to some vertex 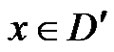 and vice versa. Hence
and vice versa. Hence 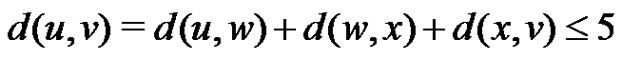 Hence
Hence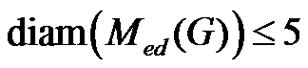 .
.
Theorem 2.15. Let 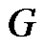 be a graph. Then
be a graph. Then 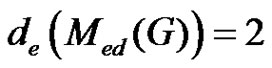 if and only if
if and only if 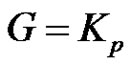 or
or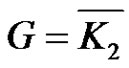 , where
, where 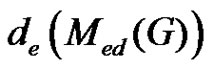 is the equitable domatic number of the graph
is the equitable domatic number of the graph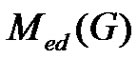 .
.
Proof. If 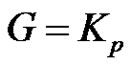 or
or , then
, then  or G = K1,2 by Proposition 2.5. Hence
or G = K1,2 by Proposition 2.5. Hence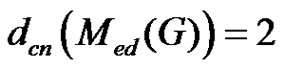 . The converse is obvious.
. The converse is obvious.
Theorem 2.16. For any graph 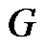 with at least one equitable isolated vertex,
with at least one equitable isolated vertex, .
.
Proof. Let  be a graph of
be a graph of 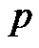 vertices, and has at least one equitable isolated vertex
vertices, and has at least one equitable isolated vertex . Then from the definition of
. Then from the definition of 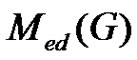 if
if 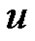 and
and  any vertices in
any vertices in 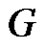 then
then 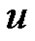 and
and 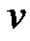 can not be adjacent in
can not be adjacent in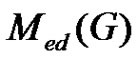 , that is there is equitable independent set containing
, that is there is equitable independent set containing 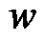 and of size
and of size , and this equitable independent will be the maximum equitable independent because
, and this equitable independent will be the maximum equitable independent because  is adjacent for all the equitable independent sets. Therefore
is adjacent for all the equitable independent sets. Therefore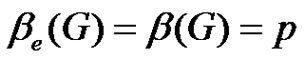 .
.
Corollary 2.17. For any graph 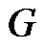 with at least one equitable isolated vertex,
with at least one equitable isolated vertex, 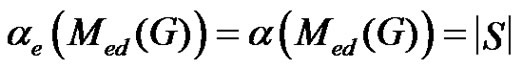 , where
, where  is the number of minimal equitable dominating set in
is the number of minimal equitable dominating set in 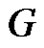
Proof. We have for any graph 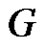 with
with 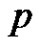 vertices
vertices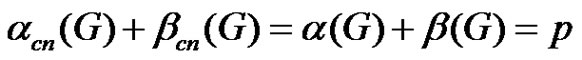 , and from [1]. Theorem 3.8.4 corollary is proved.
, and from [1]. Theorem 3.8.4 corollary is proved.
Theorem 2.18. For any graph ,
,  , if and only if
, if and only if  is complete graph.
is complete graph.
Proof. Let 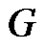 be complete graph
be complete graph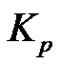 . Then from Theorem 2.16
. Then from Theorem 2.16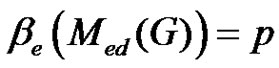 , and we have
, and we have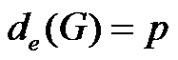 . Hence
. Hence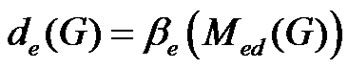 .
.
Conversely, suppose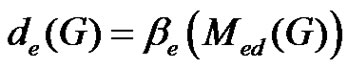 . From Theorem 2.16
. From Theorem 2.16 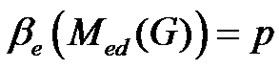 implies that
implies that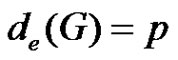 . Hence
. Hence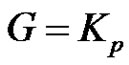 .
.
3. Acknowledgements
The authors wish to thank the referees for their helpful comments.
REFERENCES
- K. D. Dharmalingam, “Studies in Graph Theorey-Equitable Domination and Bottleneck Domination,” Ph.D. Thesis, Madurai Kamaraj University, Madurai, 2006.
- F. Harary, “Graph Theory,” Addison-Wesley, Boston, 1969.
- T. W. Haynes, S. T. Hedetniemi and P. J. Slater, “Fundamentals of Domination in Graphs,” Marcel Dekker, Inc., New York, 1998.
- V. R. Kulli and B. Janakiram, “The Minimal Dominating Graph,” Graph Theory Notes of New York, Vol. 28, Academy of Sciences, New York, 1995, pp. 12-15.
- V. R. Kulli, B. Janakiram and K. M. Niranjan, “The Common Minimal Dominating Graph,” Indian Journal of Pure and Applied Mathematics, Vol. 27, No. 2, 1996, pp. 193- 196.
- V. R. Kulli, B. Janakiram and K. M. Niranjan, “The Vertex Minimal Dominating Graph,” Acta Ciencia Indica, Vol. 28, 2002, pp. 435-440.
- V. R. Kulli, B. Janakiram and K. M. Niranjan, “The Dominating Graph,” Graph Theory Notes of New York, Vol. 46, 2004, pp. 5-8.
- H. B. Walikar, B. D. Acharya and E. Sampathkumar, “Recent Developments in the Theory of Domination in Graphs,” MRI Lecture Notes in Mathematices, Vol. 1, Mehta Research Institute, Alahabad, 1979.

