ABSTRACT

If D is a digraph, then is a quasi-kernel of D if is discrete and for each there is such that the directed distance from y to x is less than three. We give formulae for the number of quasi-kernels and for the number of minimal quasi-kernels of oriented paths and cycles.

1. Introduction

Notation For a digraph D, and denote its vertex set and arc set, respectively. If, then denotes the subdigraph of D induced by U and and denote, respectively, the inand out-neighborhoods of U. If, these latter sets may be written and.

Definition 1 A quasi-kernel K of a digraph D is a subset of satisfying two properties:

1) The quasi-absorbing property: such that the directed distance in D from y to x is either one or two;

2) Independence: there is no arc in between vertices of K.

If K is a quasi-kernel for digraph D, and and the directed distance from y to x in D is either one or two, then we will say that x quasi-absorbs y.

By [1], every digraph has at least one quasi-kernel. The number of quasi-kernels possessed by various classes of digraphs has been addressed in several papers. For example, in [2] Gutin et al. give necessary and sufficient conditions for a digraph to have at least three quasi-kernels. Clearly, any independent superset of a quasi-kernel is a quasi-kernel. In [3] we give sufficient conditions for a digraph to have at least three minimal quasi-kernels. In [4], Heard and Huang provide sufficient conditions for at least three disjoint quasi-kernels in certain classes of digraphs. In the present work, we address the problem of counting the number of quasi-kernels and the number of minimal quasi-kernels of oriented paths and cycles.

Notation For a digraph D, denotes the number of distinct quasi-kernels of D and 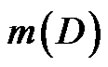denotes the number of minimal quasi-kernels of D.

Our approach is to recursively construct all quasikernels and all minimal quasi-kernels of various classes of digraphs in order to count them. The following general lemma will be useful for the examination of these special classes.

Lemma 1 If D₁ and D₂ are digraphs such that, where x is a sink in both and, then and.

Proof. Using the notation from the statement of the lemma, if is a quasi-kernel for for, then clearly satisfies the quasi-absorbing property for and D has no arcs between a vertex of and one of, so K inherits independence from and. It follows that.

If on the other hand, K is a quasi-kernel of and for, then clearly both K₁ and K₂ are independent. Since x is a sink in D, a directed path in D lies completely in D₁ or D₂. Thus the quasiabsorbing property is satisfied by K₁ in D₁ and by K₂ in D₂. It follows that every quasi-kernel of D arises as the union of a quasi-kernel of D₁ and one of D₂, so. It is clear that K₁ and K₂ are both minimal for D₁ and D₂ respectively iff is minimal for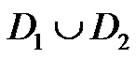, so.

2. Paths

By Lemma 1, to count the number of quasi-kernels in an arbitrary oriented path, it suffices to consider those with no internal sinks, i.e. the digraphs and defined below.

Notation

1)denotes the directed path on vertices with arc set.

2) For, denotes the result of identifying the source vertices of and. We will denote the vertices where, and, and.

3) denotes the number of quasi-kernels of containing the vertex.

There are two quasi-kernels of containing, viz. and, thus The results we obtain will be expressed in terms of the e function, so our first goal is to obtain a closed-form expression for its value. We start with a useful recursion relation.

Lemma 2 If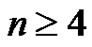, then.

Proof. If K is a quasi-kernel of containing v₁, then, by the quasi-absorbing property, K must contain either v₃ or v₄ and, by independence, K cannot contain both, nor can it contain the vertex v₂. The equation follows.

For some of what follows, it is convenient to extend the domain of the function e using the above recursion relation backwards. Thus, since and, we set 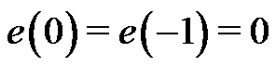and the recursion relation as stated in Lemma 2 holds for.

It is straightforward to confirm that the characteristic equation of the above recursion relation, , has the following roots:

where

The solution of the recursion relation can be written, where x₁, x₂ and x₃ are selected to satisfy the initial conditions and. The straightforward solution of the system provides the following solution. (The identity was used in obtaining these expressions.)

Theorem 1 For,

Proof. Notice that

So, since,

It can also be shown that. (We omit the details, but this follows in a straightforward way, making use of the facts that

and that. Thus, for all,

.

Since is integer valued, the result follows.

Theorem 2 For all integers and

Proof. By the quasi-absorbing property, the first vertex of a quasi-kernel of for must be v₁, v₂, or v₃, thus. Using Lemma 2 twice produces the desired equation. The first two values of n can be considered directly:

.

The only quasi-kernels of which are not minimal are those that contain both v₁ and v₃. There are clearly 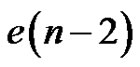of these, so. Again, the recursion relation produces the desired result.

Theorem 3 For all integers,

Proof. As noted in its definition, the digraph contains subdigraphs isomorphic to and. We will abuse the notation by using and to denote subgraphs induced by and, respectively. The set of all quasi-kernels of can be partitioned according to how the quasi-absorbing property is satisfied for the vertex s. Let K be a quasi-kernel of and consider cases.

1) K contains s.

In this case is a quasi-kernel of containing and is a quasi-kernel of containing Thus, this case contributes quasi-kernels of.

2) K contains v₂ or v₃, but not s, u₂, nor u₃.

Note that the quasi-absorbing property requires that. In this case is one of the quasi-kernels of with first vertex either v₂ or v₃ and is one of the quasi-kernes of the subgraph of induced by containing. There are

such sets K.

3) K contains u₂ or u₃, but not s = v₁, v₂ nor v₃.

This is the preceding case with m and n reversed. It contributes additional quasi-kernels.

4) K contains one vertex from 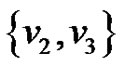and one from but does not contain s.

Here, is one of the quasi-kernels of not containing and is a quasi-kernel of not containing, of which there are. Thus we have a final

quasi-kernels.

Summing the contributions over this mutually exclusive and exhaustive list of cases:

.

The last two terms can be combined using Lemma 2 since

Theorem 4 For all integers,

Proof. Throughout this proof we follow the notation introduced on page 2. Note first that any quasi-kernel of containing the source (s) and also either v₃ or u₃ is not minimal. On the other hand, any quasi-kernel containing the source but contains neither v₃ nor u₃ must contain both v₄ and u₄. It is easy to see that such a quasikernel is minimal. Thus there are minimal quasi-kernels containing the source.

The table in Figure 1 depicts the relevant fragments of all possible quasi-kernels not containing the source. The possiblilities are sorted according to the subscripts on the v’s and secondarily to the subscript on the u’s. The leftmost column enumerates the cases for reference herein. The right-most column gives, in the case of a non-minimal quasi-kernel, an example of an extraneous vertex and, otherwise, the number of minimal quasi-kernels containing the given fragment. For example in case 1, v₂ could be removed from a quasi-kernel containing that fragment and leave a set which is still a quasi-kernel whereas in case 8, the given fragment could be extended by any of the quasi-kernels of containing v₅ and, independently, any of the quasi-kernels of containing u₃ to yield a minimal quasi-kernel of. Certain of the vertices have been left off the table if their presence in the minimal quasi-kernel is neither mandatory nor forbidden in the case depicted. For example in row 7, u₅ is not depicted since, in the configuration shown, it is present in some minimal quasi-kernels and absent in others.

Lemma 2 can be used to simplify the sum of the terms in the right column which contribute to. Thus, rows 6-8 sum to, rows 10-12 sum to and rows 13 - 14 sum to The last two of these expressions sum to, and thus we have the number of minimal quasi-kernels of which do not contain the source:

Combining this with the number already obtained for those that contain the source gives the desired result.

As stated at the beginning of this section, Theorems 2, 3 and 4 used with Lemma 1 provide the number of quasikernels and the number of minimal quasi-kernels for arbitrary oriented paths.

3. Cycles

Counting quasi-kernels for oriented cycles can almost be reduced to counting those of oriented paths. Of course any oriented cycle can be obtained by identifying the “leaf” vertices of an oriented path. The reverse process we shall call “splitting”.

Theorem 5 If x is a sink of a oriented cycle C and P is the oriented path obtained by splitting C at x, then and.

Proof. Let the two vertices of P whose identification produce x in C be and. Every quasi-kernel of a digraph must contain all the sinks of that digraph, so K is a quasi-kernel of C iff is a quasikernel of P. In particular, K is minimal for C iff is minimal for P. The result follows.

Theorem 6 If C is a oriented cycle of order n with no sink, then.

Proof. Observe first that every quasi-kernel of such a C is minimal, so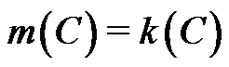. C is the result of identifying vertices v₁ and of. Use the vertex names from (v₁ for the identified vertices). If and K is a quasi-kernel for C, then there are three possibilities.

1) K contains v₁.

These quasi-kernels are exactly the images under the identification above of a quasi-kernel of containing v₁. There are of these.

2) K contains v₂.

Again, there are such quasi-kernels.

3) K contains v₃ but not v₁.

Since K contains neither v₁ nor v₂, it must contain v_n. There are therefore such quasi-kernels.

The quasi-absorbing property requires that K contain at least one of the vertices v₁, v₂ and v₃. On the other hand, independence ensures that the cases above are mutually exclusive.

REFERENCES