Optics and Photonics Journal
Vol.05 No.12(2015), Article ID:62239,15 pages
10.4236/opj.2015.512034
Intensity Distribution of the Finite Olver Beams through a Paraxial ABCD Optical System with an Aperture of Basis Annular Aperture
Salima Hennani, Lahcen Ez-Zariy*, Abdelmajid Belafhal*
Laboratory of Nuclear, Atomic and Molecular Physics, Department of Physics, Faculty of Sciences, Chouaïb Doukkali University, El Jadida, Morocco

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 October 2015; accepted 21 December 2015; published 25 December 2015
ABSTRACT
Based on the Collins diffraction formula and by means of the expansion of a hard aperture function into a finite sum of complex Gaussian functions, two analytical approaches of the Finite Olver beams (FOBs) passing through a paraxial ABCD optical system with a circular annular aperture or a rectangular one are developed in this paper. The propagation properties of the FOBs through an unapertured ABCD optical system or through this last with a circular (or rectangular) aperture or a circular (or rectangular) black screen are deduced, from the main results, as particular cases. Also, the characteristics of Finite ordinary Airy beam passing through the all considered optical systems are derived here that correspond to zeroth-order of the FOBs. According to the predicted formulas, computer simulation examples are given to deepen the understanding of the characteristics of the FOBs passing through some optical systems of annular aperture basis.
Keywords:
Diffraction, Finite Olver Beams, Airy Beams, ABCD Optical System, Circular Annular Aperture, Rectangular Annular Aperture, Circular Black Screen, Rectangular Black Screen

1. Introduction
As is well known, the Finite Airy beam, as solution of paraxial wave equation, was firstly devoted in optical field by Siviloglou et al. [1] [2] in 2007, based on the Berry publication in the context of quantum mechanics which has introduced the Airy function for the first time as solution of the Schrödinger equation [3] in 1979. Airy beams constitute a complete and orthogonal family of non diffracting beams. To date, a number of papers have been developed to study the propagation and transformation of Airy beams [1] - [8] . Siviloglou Group’s [6] - [8] was the first who had treated all theoretical and experimental properties of the Airy beams family, which allowed publishing more information on this beams class, that helped researchers to understand the behavior of this laser beams family. Recently, Belafhal et al. [9] have introduced for the first time the so-called “Finite Olver Beams” (FOBs) as theoretical generalization, with a beam order, of the ordinary Finite Airy beams. The authors have demonstrated that this novel beams class is a solution of Helmholtz equation and is a diffraction-free family [9] . In their principle reference, Belafhal et al. [9] have also devoted the phase masks for generating the beams in question in practice. For the purpose to understand and interpret the behavior of its propagation, the transformation of the FOBs by a paraxial aligned and misaligned optical system has investigated, respectively, by Hennani et al. [10] [11] in two above separate works.
Over the past twenty years, most of the optical properties of laser beams passing via annular aperture have been widely studied thanks to their theoretical and practical importance. Specifically, the focusing properties are well known when a beam is focused through various forms of apertures, whereby several theoretical studies on the propagation of laser beams through optical systems parallel to the optical axis have been made under a finite aperture condition [12] - [17] and especially the annular aperture that really exists in practice. The study of all transformations caused by the propagation of the laser beam through different forms of ABCD optical systems with annular apertures has assumed of great significance in the optics laser domain and its applications which allow describing the evaluation of a lot of laser beam characteristics [18] - [26] .
On the other hand, the propagation of Finite Airy beams through an apertured paraxial optical system characterized by a transfer matrix ABCD has attracted much practical interest in optical applications. It is expected that the intensity diffracted by various forms of apertures changes, i.e. the intensity diffracted by a circular aperture differs to that diffracted by a rectangular one. This comparison will be the aim of this work. Therefore, the answer to this question will lead us to study the behavior of the FOBs propagating through an ABCD optical system with a circular annular aperture or with a rectangular one, using the generalized Huygens-Fresnel diffraction integral and the expansion of a hard aperture function into a finite sum of complex Gaussian functions.
The paper is organized as follows: In the coming Section, an analytical expression to describe the propagation of the FOBs through an ABCD optical system with a rectangular annular aperture will be established. In the third Section, we are going to investigate and analysis the propagation properties of the FOBs through a paraxial ABCD optical system with a circular annular aperture. So, some special cases will be treated and discussed in Section 4. In Section 5, the applications of the propagation properties formulas will be illustrated with detailed numerical calculations. Finally, a simple conclusion will be planned.
2. Approach Formula of the FOBs Passing through a Paraxial ABCD Optical System with a Rectangular Aperture
In the rectangular coordinates, the electrical field distribution of two-dimensional FOBs at the waist plane situated at propagation distance 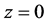 is given by
is given by
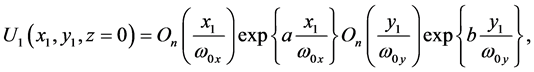 (1)
(1)
where On(.) is the Olver function of order n, 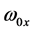 and
and 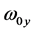 are the waist sizes of the incident beam in x and y directions, respectively. a and b are the exponential truncation factors in x and y directions, respectively. The transverse intensity distribution of the incident FOBs, for different parameters a, b and different beam orders n, is presented in Figure 1. The graphs of this figure show that the parameters a and b influence the apparition or not of the side-lobes in each direction, either x or y. This can be seen clearly around the orders n = 0 and 2. Consider now a FOBs illuminates a paraxial ABCD optical system with a rectangular annular aperture as shown in Figure 2. The rectangular annular aperture is of inner dimensional half width in x and y,
are the waist sizes of the incident beam in x and y directions, respectively. a and b are the exponential truncation factors in x and y directions, respectively. The transverse intensity distribution of the incident FOBs, for different parameters a, b and different beam orders n, is presented in Figure 1. The graphs of this figure show that the parameters a and b influence the apparition or not of the side-lobes in each direction, either x or y. This can be seen clearly around the orders n = 0 and 2. Consider now a FOBs illuminates a paraxial ABCD optical system with a rectangular annular aperture as shown in Figure 2. The rectangular annular aperture is of inner dimensional half width in x and y, 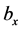 and
and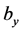 , respectively of outer dimensional half width in x and y-directions
, respectively of outer dimensional half width in x and y-directions 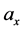 and
and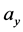 , respectively (see Figure 2). Generally, the hard rectangular aperture can be expressed with a finite sum of complex Gaussian functions as [24] [27] .
, respectively (see Figure 2). Generally, the hard rectangular aperture can be expressed with a finite sum of complex Gaussian functions as [24] [27] .



Figure 1. Transverse intensity distribution of the incident FOBs for different parameters a and b. (A): (n = 0) (a)










Figure 2. Schematic diagram of the propagation of the FOBs through an ABCD optical system with a rectangular or a circular annular aperture.

where 

Within the framework of the paraxial approximation, the propagation of a laser beam passing through a paraxial ABCD optical system over a diffraction surface


with

where 

If the diffraction surface 

Substituting Equation (1) and Equation (2) into Equation (5), we find

By using the integral representation of Olver function [9]

with
recalling the integral formula [29]


by means of the integral form [9]

and after some calculations, the output electrical field of a FOBs passing through an ABCD optical system which is limited by a rectangular annular aperture is found as follows

where


and

Equation (10) is the main first result of this work. It characterizes the transformation of a FOBs by an ABCD optical system with a rectangular annular aperture. In the following paragraph, we will focus to the propagation of FOBs through a circular annular aperture.
3. Propagation Equation of FOBs through a Circular Annular Apertured Paraxial ABCD Optical System
Let us consider a circular annular aperture located at the waist plane of 

where 


The parameters A, B, C and D are as described in Section 2. Substituting Equation (1) and Equation (14) into Equation (15), we can obtain

By using the integral representation of Olver functions given by Equation (7), recalling the integral formulae as given in Equation (8) and Equation (9), and after some calculations, we find the output optical field of a Finite Olver beam passing through an ABCD optical system with a circular annular aperture as follows

where

and

Equation (17) is considered as the main second result of this work. It characterizes the transformation of a FOBs by an ABCD optical system with a circular annular aperture. In the following paragraph, we will deduce the special cases describing the form of rectangular and circular apertures.
4. Particular Cases
4.1. Particular Cases Concerning the Incident Beam
4.1.1. Propagation of a Finite Airy Beam through a Rectangular
In this case, the propagation of this beams family passing through a paraxial ABCD optical system with rectangular annular aperture is treated. This case is obtained when 

where 
Equation (20) gives the propagation of a Finite ordinary Airy beam through an ABCD optical system apertured by a rectangular annular aperture. It is in agreement with the main result established by Equation (15) of the investigation developed by Ez-zariy et al. [24] on the transformation of the two-dimensional finite Airy beams by an ABCD optical system truncated by a rectangular annular aperture.
4.1.2. Propagation of Finite Airy Beam through a Circular Annular Aperture
The propagation of a Finite ordinary Airy beam passing through a paraxial ABCD optical system with circular annular aperture is examined as a special case when

where 
Equation (21) is obtained from Equation (17) and gives the output electrical field of a Finite Airy beam through an ABCD optical system truncated by a circular annular aperture. This equation is similar to Equation (9) regarded as the principle finding obtained by Wen et al. [5] about a Finite Airy beam traveling a paraxial ABCD optical system with circular annular aperture.
4.2. Special Cases Concerning the Rectangular Annular Aperture
4.2.1. FOBs through an ABCD Optical System with a Rectangular Aperture
In this particular case, we treat the transformation of a FOBs passing through a paraxial ABCD optical system with rectangular aperture, by choosing

with
and
4.2.2. FOBs through an ABCD Optical System with a Rectangular Black Screen
This case is obtained when
where 
Under the above conditions, the rectangular annular aperture reduces to a rectangular black screen and the transformation of FOBs passing through a paraxial ABCD optical system with rectangular black screen is characterized by the following field

When the Finite Olver beam order equal to zero, this beams family becomes a Finite Airy beam and in this situation one obtains a formula similar to that elaborated by Equation (18) of Ref. [24] .
4.2.3. FOBs through an Unapertured ABCD Optical System
An unapertured ABCD optical system conducted under the condition that 


where 
This result can be compared with that given in Ref. [10] .
4.3. Special Cases Concerning the Circular Annular Aperture
4.3.1. FOBs through an ABCD Optical System with Circular Aperture
In this case, we treat the transformation of a Finite Olver beam passing through a paraxial ABCD optical system coupled with a circular aperture. This case is obtained when 

with 
This analytical expression characterizes the propagation of a Finite Olver beam through a circular aperture followed by an ABCD optical system.
4.3.2. FOBs through an ABCD Optical System with Circular Black Screen
Under this condition

with 
4.3.3. FOBs through an Unapertured ABCD Optical System
An unapertured ABCD optical system is conducted under the condition that 


with 
This result can be compared with that given in Equation (24) and also with the principle finding of Ref. [10] .
5. Numerical Simulation Examples
5.1. Rectangular Annular Aperture
In order to investigate the effects of the rectangular (or circular) annular aperture on propagation properties of the FOBs through an ABCD optical system, some numerical simulation examples are performed in this paper using the above analytical results elaborated in Equation (10) and Equation (17) concerning the rectangular annular aperture and the circular one, respectively.
The normalized intensity distribution of the FOBs through an annular aperture followed by a free space is calculated numerically at receiver plane situated at propagation distance z. The parameters chosen in the simulations, are



where z denotes the distance between the input and output plans of the optical system.
In Figure 3, we display the normalized intensity distribution of the zeroth-order FOBs passing through an ABCD optical system with rectangular aperture. This study is investigated for making a comparison of three- dimensional behavior for different inner dimensional half width in xand y directions which are illustrated in the following way: Figure 3(A): 


















5.2. Circular Annular Aperture
In order to study the propagation characteristics of FOBs for various orders (



Figure 3. Computer simulated transverse intensity distribution of zeroth-order of FOBs passing through a rectangular annular aperture, with: (A) 




















Figure 4. Computer simulated of transverse intensity distribution of FOBs for the second order (n = 2) passing through a rectangular aperture, with: (A) 




















Figure 5. Computer simulated transverse intensity distribution of zeroth-order of FOBs passing through a circular annular aperture: (A) 


















Figure 6. Computer simulated transverse intensity distribution of FOBs for the second order (n = 2) passing through a circular annular aperture, and (A) 















ragraph as


















These figures show that there is a change in profile on the intensity distribution, which allows us to understand the transformation of the propagation of this Finite Olver beams family by changing the annular aperture size or the propagation distance in free space.
6. Conclusion
In this work, the approximate analytical representations of the Finite Olver beams passing through a paraxial ABCD optical system with rectangular annular and circular one are obtained. The method used in this paper allows us to understand the mechanism of the propagation of the Finite Olver beams by changing the aperture parameters as its size is perfected to the very small size of apertures where the real diffraction experiment cannot be performed easily. The normalized intensity distribution of this beams family in free space is graphically illustrated with numerical examples for analyzing the behavior of this beams class. Moreover, our method used in this work can be applied to other non-diffracting laser beams.
Cite this paper
SalimaHennani,LahcenEz-Zariy,AbdelmajidBelafhal, (2015) Intensity Distribution of the Finite Olver Beams through a Paraxial ABCD Optical System with an Aperture of Basis Annular Aperture. Optics and Photonics Journal,05,354-368. doi: 10.4236/opj.2015.512034
References
- 1. Siviloglou, G.A. and Christodoulides, D.N. (2007) Accelerating Finite Energy Airy Beams. Optics Letters, 32, 979-981.
http://dx.doi.org/10.1364/OL.32.000979 - 2. Siviloglou, G.A., Broky, J., Degaru, A. and Christodoulides, D.N. (2007) Observation of Accelerating Airy Beams. Physical Review Letters, 99, 213901.
http://dx.doi.org/10.1103/PhysRevLett.99.213901 - 3. Berry, M.V. and Balazs, N.L. (1979) Nonspreading Wave Packets. American Association of Physics Teachers, 47, 264.
http://dx.doi.org/10.1119/1.11855 - 4. Han, D.H., Liu, C.T. and Lai, X.Y. (2012) The Fractional Fourier Transform of Airy Beams Using Lohmann and Quadratic Optical Systems. Optics & Laser Technology, 44, 1463-1467.
http://dx.doi.org/10.1016/j.optlastec.2011.12.017 - 5. Wen, W., Lu, X., Zhao, C. and Cai, Y. (2014) Propagation of Airy Beam Passing through the Misaligned Optical System with Hard Aperture. Optics Communication, 313, 350-355.
http://dx.doi.org/10.1016/j.optcom.2013.10.056 - 6. Siviloglou, G.A., Broky, J., Dogariu, A. and Christodoulides, D.N. (2008) Ballistic Dynamics of Airy Beams. Optics Letters, 33, 207-209.
http://dx.doi.org/10.1364/OL.33.000207 - 7. Polynkin, P., Kolesik, M., Moloney, J.V., Siviloglou, G.A. and Christodoulides, D.N. (2009) Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science, 324, 229-232.
http://dx.doi.org/10.1126/science.1169544 - 8. Broky, J., Siviloglou, G.A., Dogariu, A. and Christodoulides, D.N. (2008) Self-Healing Properties of Optical Airy Beams. Optics Express, 16, 12880-12891.
http://dx.doi.org/10.1364/OE.16.012880 - 9. Belafhal, A., Ez-zariy, L., Hennani, S. and Nebdi, H. (2015) Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams. Optics and Photonics Journal, 5, 234-246.
http://dx.doi.org/10.4236/opj.2015.57023 - 10. Hennani, S., Ez-zariy, L. and Belafhal, A. (2015) Propagation Properties of Olver-Gaussian Beams Passing through a Paraxial ABCD Optical System. Optics and Photonics Journal, 5, 273-294.
http://dx.doi.org/10.4236/opj.2015.59026 - 11. Hennani, S., Ez-zariy, L. and Belafhal, A. The Analytical Representation of the Finite Olver Beams Propagating through an Apertured Misaligned ABCD Optical System.
- 12. Gu, J., Zhao, D., Mei, Z., Mao, H. and Xu, H. (2006) Propagation Characteristics of Linearly Polarized Bessel Gaussian Beams through an Annular Aperture Paraxial ABCD Optical System. Optik, 115, 529-532.
- 13. Cai, X. and Ge, D. (2006) Propagation of Various Dark Hollow Beams through an Apertured Paraxial ABCD Optical System. Physics Letters A, 357, 72-80.
http://dx.doi.org/10.1016/j.physleta.2006.04.022 - 14. Zhao, D., Mao, H., Sun, D. and Wang, S. (2005) Approximate Analytical Representation of Winger Distribution Function for Gaussian Beams Passing through ABCD Optical System with Hard Aperture. Optik, 116, 211-218.
http://dx.doi.org/10.1016/j.ijleo.2005.01.015 - 15. Gu, J., Yang, P. and Zhu, O. (2012) Propagation Characteristics of Gaussian Beams through 2×2 Square Matrix Circular Apertures. Optik, 123, 1817-1819.
http://dx.doi.org/10.1016/j.ijleo.2011.12.061 - 16. Bin, T., Fang, J.X. and Min, L.Z. (2008) Propagation of Hermite Cosh Gaussian Beams Passing through ABCD Optical System with an Annular Aperture. Optoelectronics Letters, 4, 78-80.
- 17. Abedin, K.M., Islam, M.R. and Haider, A.F.M.Y. (2007) Computer Simulation of Fresnel Diffraction from Rectangular Apertures and Obstacles Using the Fresnel Integrals Approach. Optics & Letter Technology, 39, 237-246.
http://dx.doi.org/10.1016/j.optlastec.2005.08.011 - 18. Gu, J., Zhao, D., Mei, Z., Mao, H. and Xu, H. (2004) Propagation Characteristics of Linearly Polarized Bessel Gaussian Beams through an Annular Aperture Paraxial ABCD Optical System. Optik, 115, 529-532.
http://dx.doi.org/10.1078/0030-4026-00529 - 19. Cai, X. and Ge, D. (2006) Propagation of Various Dark Hollow Beams through an Apertured Paraxial ABCD Optical System. Physics Letters A, 357, 72-80.
http://dx.doi.org/10.1016/j.physleta.2006.04.022 - 20. Duan, K. and Lü, B. (2005) Propagation of Hermite Gaussian Beams through a Paraxial Optical ABCD System with Rectangular Hard Edged Aperture. Optics Communication, 250, 1-9.
http://dx.doi.org/10.1016/j.optcom.2005.02.009 - 21. Zhao, D., Mao, H., Sun, D. and Wang, S. (2005) Approximate Analytical Representation of Winger Distribution Function for Gaussian Beams Passing through ABCD Optical System with Hard Aperture. Optik, 116, 211-218.
http://dx.doi.org/10.1016/j.ijleo.2005.01.015 - 22. Mei, M., Zhao, D., Wei, X., Jing, F. and Zhu, Q. (2005) Propagation of Bessel-Modulated Gaussian Beams through a Paraxial ABCD Optical System with an Annular Aperture. Optik, 116, 521-526.
- 23. Wang, W., Ning, Y.Q., Tian, Z.H., Zhang, X., Shi, J.J., Wang, Z.F., Zhang, L.S., Zhang, Y., Liu, Y., Qin, L. and Wang, L.J. (2011) Coherent Polarization Stabilization in Large Aperture Rectangular Post Bottom Emitting Vertical Cavity Surface Emitting Lasers. Optics Communication, 284, 1335-1338.
http://dx.doi.org/10.1016/j.optcom.2010.11.014 - 24. Ez-zariy, L., Nebdi, H., Boustimi, M. and Belafhal, A. (2014) Transformation of a Two-Dimensional Finite Energy Airy Beam by an ABCD Optical System with a Rectangular Annular Aperture. Physical and Chemical News, 73, 39-49.
- 25. Mei, Z., Zhao, D., Gua, J. and Mao, H. (2004) Approximate Analytical Expressions of Laguerre-Gaussian Beams Passing through a Paraxial Optical System with an Annular Aperture. Optik, 115, 311-316.
- 26. Gu, J., Yang, P. and Zhang, Y. (2013) The Intensity Distribution of Hermite-Gaussian Beam through an Annular Aperture. Optik, 124, 5858-5862.
- 27. Wen, J.J. and Breazeale, M.A. (1998) A Diffraction Beam Field Expressed as the Superposition of Gaussian Beams. Journal of the Acoustical Society of America, 83, 1752-1756.
http://dx.doi.org/10.1121/1.396508 - 28. Collins, S.A. (1970) Lens-System Diffraction Integral Written in Terms of Matrix Optics. Journal of the Optical Society of America, 60, 1168-1170.
http://dx.doi.org/10.1364/JOSA.60.001168 - 29. Gradshteyn, I.S. and Ryzhik, I.M. (1994) Tables of Integrals Series and Products. 5th Edition, Academic Press, New York.
NOTES
*Corresponding author.




















