Optics and Photonics Journal
Vol.05 No.07(2015), Article ID:58309,6 pages
10.4236/opj.2015.57022
Analysis of the Effect of Air Hole Diameter and Lattice Pitch in Optical Properties for Hexagonal Photonic Crystal Fiber
Sagor Biswas, Ragib Shakil Rafi, Md. Abdullah Al-Amin, Sabbir Alam
Electronics and Communication Engineering (ECE) Discipline, Khulna University, Khulna, Bangladesh
Email: ku.08rafi@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 June 2015; accepted 24 July 2015; published 27 July 2015
ABSTRACT
We have investigated the different optical properties such as confinement loss, waveguide dispersion of a five rings hexagonal photonic crystal fiber under varied air hole diameter (d), lattice pitch (Λ), and air hole diameter to lattice pitch ratio for three different materials fused quartz glass, borosilicate glass and sapphire glass. We observed low confinement loss and high negative dispersion at higher d/Λ. Achieving high d/Λ can be done in two ways: increasing the air hole diameter or decreasing the lattice pitch. It has been observed, increasing the air hole diameter has significant effect over reducing lattice pitch in achieving low confinement loss. On the other hand, decreasing the lattice pitch over increasing the air hole diameter has significant effect in achieving high negative dispersion. It has also been found that, effective refractive index ( ) decreases significantly when lattice pitch decreases.
Keywords:
Photonic Crystal Fiber, Dispersion, Air Hole Diameter, Lattice Pitch, Effective Refractive Index

1. Introduction
Photonic Crystal Fiber (PCF) is a new class of fiber gaining much attention to the researchers due to its design flexibility and wide application areas [1] -[4] . PCFs are now being used to make optical oscillators, amplifiers and fiber lasers. Basically in photonic crystal fiber, many air holes are arranged in a periodic manner that gives them a crystal like structure. By changing the internal air hole arrangement and their diameter, new types of PCFs are being produced for different application areas [5] . Photonic crystal fiber shows optical properties like high nonlinearity, high negative dispersion, low confinement loss etc. [6] [7] . Air hole diameter (d) and lattice pitch (Λ) are two very important factor of designing PCF. In achieving the high negative dispersion or low confinement loss, air hole diameter to lattice pitch ratio can be tailored to redesign the internal structure of the PCF [8] . However, air hole diameter or lattice pitch which one shows significant effect on redesigning the fiber is an important question and also the change of these parameters may have an important relationship with the effective refractive index. In solid core Photonic crystal fiber, core has high effective refractive index which exhibits strongly wavelength dependence [9] [10] . With the increase of wavelength, the refractive index decreases. In PCFs, by changing its internal structure, dispersion property and confinement loss can be reengineered. These are related with the complex effective refractive index and the effective refractive index depends on wavelength and internal structure of PCF. So, with the change of operating wavelength, air hole diameter and lattice pitch, the effective refractive index changes as well as dispersion and confinement loss [11] [12] . The main goal of this paper is to understand the effect of air hole diameter and lattice pitch on these optical properties. If the trend of their influence can be analyzed, then better photonic crystal fiber can be produced with changed internal architecture. This paper is summarized as follows: Section 2 explains materials and methods, Section 3 shows and describes the simulation results. Finally, Section 4 concludes the paper and section 5 will give an idea about our future works.
2. Materials and Methods
In this thesis, we have designed Photonic Crystal Fiber of five rings hexagonal structure in Opti-FDTD software (version 8). Three types’ different materials are used here. The materials are Borosilicate glass (n = 1.47), Fused quartz (n = 1.46), and Sapphire glass (n = 1.762). We created these structures for air hole diameter (0.60, 0.65, 0.70, 0.75, 0 .80) µm, and for lattice pitch (2.3, 2.14, 2, 1.81, 1.71) µm. We took five different d/Λ ratios (0.26, 0.28, 0.30, 0.32, 0.34) for our simulation. Optical properties such as effective refractive index, confinement loss, and waveguide dispersion are measured calculated under wavelength ranges from 750 nm to 1600 nm. Waveguide dispersion is calculated from the following equation:
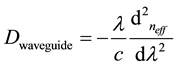 (1)
(1)
Here, λ is the wavelength and c is the velocity of light in free space. Second derivation of effective refractive index is calculated using numerical method. According to the numerical method, at first left right slope for each value of effective refractive index is calculated and then averaging those values gave us the first derivative value. Repeating the process, we got the second derivative. Confinement loss is calculated from the following equation:
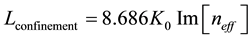 (2)
(2)
Here, 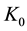 is the wave number and
is the wave number and 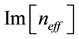 is the imaginary part of effective refractive index. These curves are then investigated to reach in a certain decision. The simulation is done in two steps. At the first step, we used OPTI FDTD 8 software for creating the hexagonal photonic crystal fiber for three different materials. OPTI FDTD 8 software simulation gives us the complex effective refractive index which has a real part and an imaginary part. In the second step, we used these values to calculate dispersion and confinement loss, and MATLAB was used to plot the result.
is the imaginary part of effective refractive index. These curves are then investigated to reach in a certain decision. The simulation is done in two steps. At the first step, we used OPTI FDTD 8 software for creating the hexagonal photonic crystal fiber for three different materials. OPTI FDTD 8 software simulation gives us the complex effective refractive index which has a real part and an imaginary part. In the second step, we used these values to calculate dispersion and confinement loss, and MATLAB was used to plot the result.
3. Results and Discussions
Basically, effective refractive index ( ) is a wavelength dependent parameter. But in photonic crystal fiber, internal stricter of the fiber also affect the change of effective refractive index. We took the effective refractive index data for three different materials like fused quartz glass, borosilicate glass, sapphire glass under different diameter and pitch condition. When we changed the diameter, we kept pitch constant and kept diameter constant when we changed pitch of the PCF. We tried to focus on the variation of effective refractive index due to hole diameter and pitch change.
From the previous Figures 1-4, we observed that, effective refractive index changes more quickly with the change of pitch than the change of hole diameter. The percentage of change in effective refractive index increases with the increase in wavelength as well as hole diameter, and pitch but it changes more with the lattice pitch. Similar type of result has been found for all three glasses. As, effective refractive index change show dif-
Figure 1. Hexagonal photonic crystal Fiber.

Figure 2. Variation of effective refractive index with wavelength under various diameter to pitch ratio for fused silica glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 3. Variation of effective refractive index with wavelength under various diameter to pitch ratio for borosilicate glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 4. Variation of effective refractive index with wavelength under various diameter to pitch ratio for Sapphire glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).
ferent values for different air hole diameter and lattice pitch, these two must have different effect in optical properties like confinement loss and dispersion.
It is obvious form the Figures 5-7 that, confinement loss decrease with the increase of air hole diameter. On the other hand, confinement loss increases with the decrease of pitch. Low values of confinement loss are observed, when we change the air hole diameter. From the figure, value of confinement loss for sapphire glass at 1600 nm wavelength is about 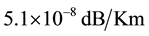 when hole diameter is 0.80 µm. Keeping the same hole diameter to pitch ratio, we got confinement loss for sapphire glass at 1600 nm wavelength is about
when hole diameter is 0.80 µm. Keeping the same hole diameter to pitch ratio, we got confinement loss for sapphire glass at 1600 nm wavelength is about 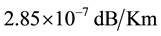 when pitch is 1.71 µm, which is about 5.5 times larger than the earlier one. Low confinement loss is achieved at higher air hole diameter to pitch ratio. We got the similar type of results for the other two glass material.
when pitch is 1.71 µm, which is about 5.5 times larger than the earlier one. Low confinement loss is achieved at higher air hole diameter to pitch ratio. We got the similar type of results for the other two glass material.
Another very important design parameter is waveguide dispersion. From the following figures, we see that for same parameters when we increase the air hole diameter, high negative dispersion is achieved. But more negative dispersion is attained when we decrease the pitch of photonic crystal fiber. PCF with higher refractive index material has high negative waveguide dispersion which is sometimes desirable in communication field. So, if we use materials of high effective refractive index, it will provide high value of negative waveguide dispersion. Figures 8-10 show results related to dispersion.
So, when we focus both on confinement loss and dispersion, it’s better to use high air hole diameter as it provides low confinement loss and high negative dispersion for the same diameter to pitch ratio. On the other hand, low confinement loss and high negative dispersion is achievable for high air hole diameter to pitch ratio.
4. Conclusion
In this paper, we have created different layout of hexagonal photonic crystal fiber based on different air hole diameter and lattice pitch. We created the layout for three different materials having different refractive index. We have also studied the optical parameters like confinement loss and waveguide dispersion by varying the structure of PCFs. The effective refractive index in which confinement loss and dispersion are depended, decreases more rapidly for decreasing the lattice pitch rather than increasing the hole diameter. From confinement loss analysis, we can say that for higher wavelength, low confinement loss is achieved with high air hole diameter to pitch ratio and we can achieve this high ratio either by increasing air hole diameter or by decreasing the lattice pitch. But increasing the air hole diameter is more effective than decreasing the lattice pitch to get low confinement loss. Also high negative dispersion is achieved at high air hole diameter to pitch ratio. Here we also can achieve this high ratio either by increasing air hole diameter or by decreasing the lattice pitch. But decreasing the lattice pitch is more effective than increasing the air hole diameter to get high negative dispersion. So, there is dissimilarity in between confinement loss reduction and achieving high negative dispersion. So, a tradeoff must be made between confinement loss and high negative dispersion. On the other hand, high negative dispersion is attained when we used high refractive index material like sapphire glass. So, to achieve high negative

Figure 5. Variation of confinement loss with wavelength under various diameter to pitch ratio for fused silica glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 6. Variation of confinement loss with wavelength under various diameter to pitch ratio for borosilicate glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 7. Variation of confinement loss with wavelength under various diameter to pitch ratio for sapphire glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 8. Variation of waveguide dispersion with wavelength under various diameter to pitch ratio for fused silica glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 9. Variation of waveguide dispersion with wavelength under various diameter to pitch ratio for borosilicate glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).

Figure 10. Variation of waveguide dispersion with wavelength under various diameter to pitch ratio for sapphire glass. (a) variation due to the air hole diameter (pitch constant) (b) variation due to lattice pitch (diameter constant).
dispersion, we can reengineered the core refractive index with higher values. This high negative dispersion is important for telecommunication applications.
5. Future Works
We only worked with hexagonal shape photonics crystal fiber is this paper. In near future, we will design layout of PCFs with rectangular, circular, triangular, square shapes and will analysis the confinement loss, chromatic dispersion, mode field diameter, effective area, bending loss, birefringence etc under various air hole diameter and lattice pitch. More advance study will be carried out to insert other materials in the core region and analysis the propagation parameters. Moreover, we also hope to study about the fabrication of our photonics crystal fiber model with low cost and application demand.
Cite this paper
SagorBiswas,Ragib ShakilRafi,Md. AbdullahAl-Amin,SabbirAlam, (2015) Analysis of the Effect of Air Hole Diameter and Lattice Pitch in Optical Properties for Hexagonal Photonic Crystal Fiber. Optics and Photonics Journal,05,227-233. doi: 10.4236/opj.2015.57022
References
- 1. Wong, G.K.L., Chen, A.Y.H., Ha, S.W., Kruhlak, R.J., Murdoch, S.G., Leonhardt, R., Harvey, J.D. and Joly, N.Y. (2005) Characterization of Chromatic Dispersion in Photonic Crystal Fibers Using Scalar Modulation Instability. Optics Express, 13, 8662-8670.
- 2. Arakaki, K., Namihira, Y., Kinjo, T., Kaijage, S.F., Razzak, S.M.A. and Nonogaki, Y. (2009) Dispersion Controlled Highly Nonlinear Octagonal Photonic Crystal Fiber (Pcf) for Medical Applications. Proceedings of the 14th Optoelectronics and Communications Conference (OECC), Hong Kong, 13-17 July 2009, 1-2.
http://dx.doi.org/10.1109/oecc.2009.5214745 - 3. Agarwal, P. (2013) Modeling of Elliptical Air Hole Pcf for Lower Dispersion. Advance in Electronic and Electric Engineering, 3, 439-446.
- 4. Buczynski, R. (2004) Photonic Crystal Fibers. Acta Physica Polonica Series A, 106, 141-168.
- 5. Olyaeea, S., Sadeghib, M. and Taghipoura, F. (2012) Design of Low-Dispersion Fractal Photonic Crystal Fiber. International Journal of Optics and Photonics, 6, 57-64.
- 6. Jalal Uddin, M. and Shah Alam, M. (2008) Dispersion and Confinement Loss of Photonic Crystal Fiber. Asian Journal of Information Technology, 7, 344-349.
- 7. Yang, S.G., Zhang, Y.J., Peng, X.Z., Lu, Y., Xie, S.Z., Li, J.Y., Chen, W., Jiang, Z.W., Peng, J.G. and Li, H.Q. (2006) Theoretical Study and Experimental Fabrication of High Negative Dispersion Photonic Crystal Fiber with Large Area Mode Field. Optics Express, 14, 3015-3023.
- 8. Kim, T.-H. (2010) Design, Fabrication, and Sensor Applications of Photonic Crystal Fibers. Journal of the Korean Physical Society, 57, 1937-1941.
- 9. Olyaee, S. and Taghipour, F. (2011) A New Design of Photonic Crystal Fiber with Ultra-Flattened Dispersion to Simultaneously Minimize the Dispersion and Confinement Loss. Journal of Physics: Conference Series, 276.
- 10. Nozhat, N. and Granpayeh, N. (2009) Specialty Fibers Designed by Photonic Crystals. Progress in Electromagnetics Research, 99, 225-244.
- 11. Sharma, Y. and Zafar, R. (2014) Ultra Flattened Dispersion over Telecom Wavelength in Ring Based Photonic Crystal Fiber. IOSR Journal of Electronics and Communication Engineering, 9, 11-14.
- 12. Namihira, Y., Hossain, Md.A., Liu, J.j., Koga, T., Kinjo, T., Hirako, Y., Begum, F., Kaijage, S.F., Razzak, S.M.A. and Nozaki, S. (2011) Dispersion Flattened Nonlinear Square Photonic Crystal Fiber for Dental Oct. IET International Conference on Communication Technology and Application (ICCTA), Beijing, 14-16 October 2011, 819-823.


