Received 23 September 2014; revised 18 October 2014; accepted 11 November 2014

ABSTRACT

Propagation characteristics of finite Airy-Gaussian beams through an apertured misaligned first- order ABCD optical system are studied. In this work, the generalized Huygens-Fresnel diffraction integral and the expansion of the hard aperture function into a finite sum of complex Gaussian functions are used. The propagation of Airy-Gaussian beam passing through: an unapertured misaligned optical system, an apertured aligned ABCD optical system and an unapertured aligned ABCD optical system are derived here as particular cases of the main finding. Some numerical simulations are performed in the paper.

Keywords:

Airy-Gaussian Beams, Huygens-Fresnel Diffraction Integral, Aperture, Misalignment

1. Introduction

Airy beam is initially predicted theoretically, in quantum physics, as a solution of force-free Schrödinger equation by Berry and Balazs [1] in 1979. It is a non-spreading wave packet that remains invariant during propagation and contains infinite energy. Airy beam can exhibit a self-healing property after being obscured by an obstacle placed in its propagation path [2] and a self-accelerating feature even in the absence of any external potential [3] . Yet, Airy beam is propagating along parabolic trajectory, while preserving its amplitude structure indefinitely [4] . The original Airy beam which contains infinite energy is not realizable in practice. However, in 2007, Siviloglou et al. [3] and Siviloglou and Christodoulides [5] have started the first observation of Airy optical beam that presents a finite energy and demonstrates experimentally the unusual features of the new finite Airy beam. In the literature, several methods were used to produce the finite Airy beam, including cubic phase, 3/2 phase only pattern [6] -[9] , and three-wave mixing processes in an asymmetric nonlinear photonic crystals [10] [11] . In the past few years, the propagation characteristics of Airy family have been examined widely in free space [12] [13] , in fractional Fourier transform and quadratic index medium [13] - [16] , in turbulence [17] [18] , in a unixial crystals [19] and in other media [20] - [22] . Among of these, in [13] , Bandres and Gutierrez- Vega have introduced for the first time, the so-called generalized Airy-Gaussian beam and treated its propagation properties through different complex paraxial optical systems characterized by ABCD matrices. This generalized Airy-Gaussian beam carries a finite energy and can be realized experimentally. The Airy beam devoted by Berry and Balazs [1] and the finite Airy invented and produced by Siviloglou et al. [3] [4] are regarded as special cases of the study of Bandres and Gutiérrez-Vega [13] .

On the other hand, most practical optical systems are more or less slightly misaligned, due to displacement or angle misalignment. Then, it is necessary to take the misalignment of the optical system into consideration. Various laser beams passing through misaligned optical systems with or without aperture have been treated by researchers [23] - [30] . To the best of our knowledge, the research of Airy-Gaussian beam propagating through an apertured misaligned optical has not been reported elsewhere.

In this paper, by expanding a hard-edged aperture function into a finite sum of complex Gaussian functions and the generalized Huygens-Fresnel diffraction integral, an approximate formula for the propagation of Airy- Gaussian beam in any misaligned optical system with a hard-edged aperture is developed in the coming section. The propagation of Airy-Gaussian beam through: unapertured misaligned, unapertured and apertured aligned optical systems are deduced as particular cases in Section 3. Some numerical results are performed and discussed in Section 4. The work is finished by a simple conclusion in Section 5.

2. Theory

The field distribution 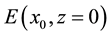of finite Airy-Gaussian beam at plane source in the rectangular coordinate system is expressed as follows [13] [3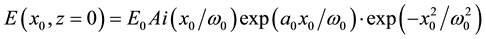1]

, (1)

where is the Airy function of the first kind, is the waist width (is a characteristic parameter of finite Airy beam) at waist plane 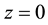and is the modulation parameter (aperture coefficient).

Figure 1 illustrates a comparison between intensity distributions of finite Airy beam and finite Airy-Gaussian beam for different aperture coefficients 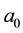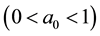. Depicted plots show that ideal Airy beam (finite Airy beam with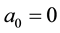) carry an infinite energy and its intensity profile presents infinity of oscillations, side-lobes and zeros in the negative part of the transverse 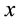-coordinate and principle lobe shifted from the propagation axis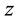. Intensity oscillations vanish gradually with the increase of 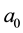and totally disappear when 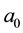approaches to 1. A modulation of finite Airy beam by a Gaussian transmittance avoid the oscillations and secondary lobes whatever value of. Furthermore, it should be noted that the intensity maximum decreases with the increasing of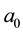, in the both cases: finite Airy and finite Airy-Gaussian beams. However, the velocity of diminution of intensity amplitude of finite Airy beam modulated by Gaussian envelope is very small compared with that of no-modulated one. Also, an increasing in 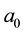leads to a movement of principle lobe towards optical axis for.

Assuming a hard-edge rectangular aperture of radius a located at waist plane of. The corresponding window is

(2)

According to the method proposed by Wen and Breazeale [32] , the hard-edged function can be expanded into a finite sum of complex Gaussian functions [23] [32] as

, (3)

where and are the expansion and Gaussian coefficients, respectively, which could be obtained by optimization-computation directly. is the number of complex Gaussian terms.

Now, let us consider a misaligned optical system ABCD as schematized in Figure 2. The transformation of a light laser beam by such optical system with an aperture is expressed by the generalized Huygens-Fresnel dif-

fraction integral formulae for a misaligned optical system of the form [23] [33] - [35]

, (4)

where is the wave number and being the wavelength.

The coefficients A, B and D are elements of transfer matrix corresponding to the ABCD optical system after the aperture. is the finite hard aperture function. The parameters E and G are elements characterizing the system misalignment and take the following expressions

, (5a)

, (5b)

where is the displacement and is the tilting angle of the element., , and represent the misaligned matrix elements determined by

, (6a)

, (6b)

, (6c)

and

. (6d)

Substituting Equations (1) and (3) into Equation (4), the exiting beam in the observation plane of the apertured misaligned optical system is obtained as

, (7)

where

. (8)

In order to determine the above integral (7), the Airy function can be rewritten into representation integral as [36]

. (9)

Inserting this equation into Equation (7) the field distribution of the outgoing beam of a finite Airy-Gaussian beam passing from an apertured misaligned optical system becomes

(10)

By means the well known integrals [36] [37]

, (11)

and

, (12)

the exiting electric field of a finite Airy-Gaussian beam propagating through an apertured misaligned optical system is obtained as

(13)

This last equation is the main result of the current work. It is the general analytical expression of the outgoing electric field of a finite Airy-Gaussian beam propagating through an apertured misaligned optical system at the receiver plane. From this result, it can easily be seen that the out-put beam at the observation plane of the misaligned optical system becomes decentred. The principle spot center is deviated away from the origin of the emitted plane by in transverse -direction coordinate.

3. Particular Cases

3.1. Unapertured Misaligned Optical System

This special case can be obtained when, under this condition Equation (13) reduces to

(14)

This is the formula of an Airy-Gaussian beam passing through an unapertured misaligned optical system.

3.2. Apertured Aligned Optical System

When, one find that the misalignment parameters are null, , the optical system arrives aligned and Equation (13) reduces to

(15)

This is the analytical formula of outgoing electric field of the Airy-Gaussian beam passing through an aligned paraxial ABCD optical system with a finite hard aperture.

3.3. Unapertured Aligned Optical System

This situation could be obtained if and. Under these conditions, Equation (13) becomes

(16)

This closed-form expression characterizes the propagation of Airy-Gaussian beam through an unapertured aligned paraxial ABCD optical system.

4. Numerical Simulations and Discussions

According to the obtained analytical expression established in Equation (13), the properties of an Airy-Gaussian beam through an apertured misaligned optical system are investigated numerically in this section. Let us consider an Airy-Gaussian beam propagating through an apertured misaligned circular thin lens placed at waist plane, , followed by a free space. The matrix corresponding to this optical system has the form

, (17)

where is the axial distance between the plane waist and the thin lens. In our situation, we take, is the thin lens focus length, and is the distance from the input plane to the observation plane (is the propagation distance). The parameters used in the simulations are: the wavelength, the waist size of the incident beam, the angle misalignment of the lens with respect to the optical propagation axis chosen as. The misalignment parameters, , and take the following expressions

, (18)

and the corresponding parameters E and G are

. (19)

In order to validate the theoretical finding, in the following we will discuss the effect of some factors including elements system displacement, propagation distance and thin lens focal length on deviation of the out-put beam at the observation plane.

Figure 3 displays the normalized intensity of finite Airy-Gaussian beam through an apertured misaligned

optical system versus the transverse coordinate for different elements displacement. The other parameters are fixed at, and. From the curves of this figure, it appears that the center of this exiting beam is shifted effectively. Elements optical displacements, 0.3, 0.5, 1 and 2 mm lead to deviation of exiting beam by, 0.6, 1.2 and 4 mm, respectively. Theses deviations correspond, in each time, to .

Figure 4 is the same as Figure 3, but in this time for fixed, and and for different propagation distances, 250, 500 and 750 mm. Their corresponding outgoing beam displacements are, 1, 2 and 4 mm, respectively.

Figure 5 is similar to Figure 3 and Figure 4, but in this time for fixed, and and for various propagation distances. The centre of the output beam is shifted inversely in proportion to the thin lens focal length f = 125, 250, 500 and 750 mm lead to exiting beam shift , 2, 1 and 0.5 mm.

Generally, a displacement of element optical system affects a shift of the exiting beam. The deviation degree increases with an increase in elements optical system displacement or with a fixed accompanied with an augmentation in propagation distance or diminution in thin lens focal length. The deviation quantity is proportional to optical system elements displacement, to propagation distance and inversely proportional to thin lens focal length.

Practically, the misalignment of the optical system can be a tool or a technique for the determination of a thin lens focal length. Knowing the elements displacement and propagation distance and the coordinates of

the center of exiting spot and with help the relationship, one can easily deduce.

To consolidate our theoretical and numerical finding concerning the deviation of the exiting beam from a misaligned optical system, we display in Figure 6 the cross three-dimensional intensity distribution of the outgoing finite Airy-Gaussian beams intensity along the meridian plane. From the plots of this figure, we can find that the deviation degree of the beam in -direction depends on the displacement quantity. For an indicated point located at coordinates, the deviation degree of the spot is proportional to optical system displacement.

5. Conclusion

Based on the generalized Huygens-Fresnel diffraction integral and by expanding of the hard edged aperture function into a finite sum of complex Gaussian functions, we have come up with an approximate analytical expression for determining and analyzing the propagation properties of finite Airy-Gaussian beam through an apertured misaligned optical system. This study generalizes the cases of propagation of Airy-Gaussian beam through unapertured misaligned optical system, apertured aligned optical system and unapertured aligned optical system, which are regarded as special cases of our main investigation. The numerical simulations developed

in the paper show that the exiting beam keeps similar properties of its incident beam but it shifts from the propagation axis.

References

NOTES

^*Corresponding author.