Optics and Photonics Journal
Vol.3 No.7A(2013), Article ID:40131,6 pages DOI:10.4236/opj.2013.37A003
Could the Cuticle of Beetles Serve Also for Their Radiative Thermoregulation?
1Center for Optics, Photonics and Laser, Department of Physics, Engineering Physics and Optics, Laval University, Québec City, Canada
2Department of Physics, Yerevan State University, Yerevan, Armenia
Email: *galstian@phy.ulaval.ca
Copyright © 2013 Karen Allahverdyan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 17, 2013; revised August 19, 2013; accepted September 26, 2013
Keywords: Light Propagation in Tissues; Photonic Band-Gap Materials; Optical Properties
ABSTRACT
Based on the recent observation of the asymmetry of light energy flow through a material system that is similar to an iridescent beetle’s cuticle, we discuss the key roles of chiral molecular organization (responsible for the iridescent color of beetles) and of asymmetric boundary conditions (defined by the position of their cuticle) in the evolution of such photonic biological structures. Question is raised about the possible role of such energy flow asymmetry in the radiative thermoregulation of those beetles.
1. Introduction
Color is omnipresent in the biological world and the mechanisms of its generation by absorption (pigment based) or by the structural (periodic) modulation are rather well known (see, e.g., Ref. [1] and references therein). It is also well known that the structural color mechanism may generate iridescent (angle dependent) colors. Particularly interesting, in this family, are the cases of helicoidal (chiral) structures, frequently found in beetle cuticles [1,2]. In some of those cases (e.g., for the P. optima [2]), the cuticle has a solid material layer made with helicoidally aligned molecules; the axis of that helix pointing towards the normal of the cuticle. In fact, the layer in question is a self-assembly of multiple molecular monolayers. The molecules are oriented in the same direction (described by a unit vector n) in each of those locally uniaxial anisotropic monolayers. The direction of n in each monolayer is oriented at slightly different angle with respect to the n of the previous molecular monolayer. Those molecular assemblies may be compared with an optical mirror that reflects circularly polarized light bi (having the same helicicity as the molecular alignment, further called resonant polarization) and transmits light ai having the opposed helicicity, Figure 1(a). In addition, given the interferential character of reflection, this layer is wavelength selective and is generating an iridescent color of the beetle when observed at different angles (colors shifting to blue with higher angles). Very often these layers are compared to the frozen form of cholesteric liquid crystals (CLC) [1,3,4]. While the operation principle of such layers was well detailed in the scientific literature, to the best of our knowledge, there was no analysis of their biological origins in the beetle cuticle. In fact, the presence of such a layer could be explained by the abundance of chiral molecules such as chitin derivatives [1]. However, in some cases (e.g., the P. resplendens [2]), the cuticle contains a sequence (combination) of three layers (Figure 1(c)): the first one made with helicoidally aligned molecules (as described above), followed by a second layer (see Figure 1(b)) that is composed of uniformly aligned molecules (e.g., uric acid) and finally a third layer that also has helicoidally aligned molecules, with slightly different periodicity but with the same helicicity as the first one (Figure 1(a)). From the optical point of view, the second layer (Figure 1(b)) may play the role of so called “half wave plate” (i.e., with thickness d and local optical anisotropy of the material Dn chosen in such way that the differential phase delay is equal to p) that transforms the circular polarization of the incident light gi with given helicicity into its opposed helicicity in the transmitted light gt. This combination (Figure 1(c)) of two polarization and wavelength selective mirrors with the half wave plate (between them) is a rather complex optical system (see, e.g. [5]). We think that, there must be an evolutionary reason (a selective advantage in natural selection) why those beetles have developed such a structure.
Of course the first manifestation (to the human eye) of the “function” of this combined triple-layer structure is optical: generation of strong iridescent color of the beetle. Several reasons have already been discussed for the color development in the biological world: camouflage [6], sexual attraction [7] and aposematism [8] are among the most cited ones. It is worth to note that all above mentioned functions may be obtained also by simple pigmentation (absorption of specific wavelengths). However, in contrast to the pigment based coloration, the periodic helicodial nature of molecular organization introduces three specific properties of light reflection from such a structure. First of all this is the polarization dependence of reflection; and a question naturally rises: is there any

Figure 1. Schematic presentation of various “optical” layers composing the beetle cuticle (bold linear double arrows show the local orientation of optical axes; dashed horizontal layer shows the axes of the helix; thin solid and dotted arrows show light propagation directions; curved arrows show the circular polarizations of opposed sign for (a) single helicoidal structure of P. optima (only one period P0 of complete molecular rotation is shown for simplicity), where ai and at correspond, respectively, to the incident and transmitted light of non-resonant helicicity, bi and br correspond, respectively, to the incident and reflected light of resonant helicicity; for (b) single uniaxial anisotropy structure with thickness d and local anisotropy Dn, where gi and gt correspond, respectively, to the incident and transmitted light of opposed helicicity, and for (c) combined “helicoidal-planarhelicoidal” structure of P. resplendens.
specific biological function that the polarization dependence enables in addition? (As a matter of fact, it was shown that there are some crustaceans with circular polarization discriminated vision [9]). The second specificity is the minimization of light absorption by the beetle cuticles in the case of structural coloration (by reflection).
This could reduce the heat generation due to absorption. Finally, this reflection is often spectrally narrowband (with a typical spectral width of DlR » 50 nm), but the central (or resonant) wavelength of light reflection lR is typically centered in the visible spectral band where sun has maximum spectral power.
2. Materials & Sample
Based on a recent observation of optical non-reciprocity in a slab of CLC [10], we first show (in the present work) that in addition to the well-known iridescent reflection of circularly polarized light, the beetle cuticle should possess another interesting property: light transmission coefficients in and out from the beetle’s body should be different. This phenomenon is then analyzed as a possible evolutional development mechanism of such helicoidal structures: the energy regulation. Indeed, each of the described above optical layers is known to be optically reciprocal (that is, light transmission is the same in opposed directions of propagation) when they are standalone. However, given the specific position of the beetle cuticle, its boundary conditions are optically asymmetric since the outside world (air) and sub-cuticle (body) constituents of the beetle have quite different optical properties, Figure 2. As we have shown recently [10], light transmission then may become strongly asymmetric (non-reciprocal), which, for the beetle would mean that the non-resonant electromagnetic energy flow is stronger in one direction (from the center of beetle’s body towards outside) than in the opposed direction. This, in turn, could create improved heat evacuation in stressful light conditions (high intensity and long exposure), in a way, opposite to the traditional “greenhouse” effect (when more energy enters the system than exits).
A brief description of the work performed to experimentally demonstrate this effect of non-reciprocal transmission follows (see also [10]). We have constructed CLC cells with asymmetric boundary conditions (as cuticle “models”). To create such asymmetric cells, we have built sandwiches where the CLC layer was confined between two substrates having unidirectional rubbed polyimide (PI) layers coated on internal sides of beetle’s substrates [4,11-13]. Only one of those substrates had an ITO coating between the substrate and the PI layer (such cells are used for lens fabrication [14]), providing thus optically asymmetric boundary conditions for the CLC layer (see Figure 3). The first substrate was made from a standard microscope glass with 1 mm of thickness, while the second one was an ITO coated glass of 0.7 mm thickness. Cells were fabricated by spacing the two above mentioned substrates at 8 μm distance (using spacers dispersed in the peripheral glue walls) and by using the standard method of capillary injection of the CLC mixture (see below).
To obtain stronger reflection from the ITO layer (compared to the uncoated glass), we have decided to make our demonstration in the near infra-red (NIR) spectral band for which the Fresnel reflections of our ITOs are significantly higher compared to the NIR light reflection from the simple glass interface. Thus, it was necessary to use a CLC mixture that would have a resonant reflection band in the NIR area. This mixture was obtained by adding 33 wt% of CB15 molecules and 67 wt% of MLC 2048 mixture (both purchased from Merck). The first component (CB15) is a right handed chiral composition (not disclosed by Merck). Note that the period P0 of molecular rotation (when molecules of various consecutive monolayers rotate by 360˚) of CLC is related to the reflection bandwidth DlR and to the wavelength lR of resonant reflection, respectively, by equations DlR = P0 Dn and lR = P0 nav, where Dn is the local anisotropy

Figure 2. Schematic presentation of the helicoidal layer (only one period of molecular rotation is shown) and its asymmetric boundary conditions in the case of beetle cuticle.
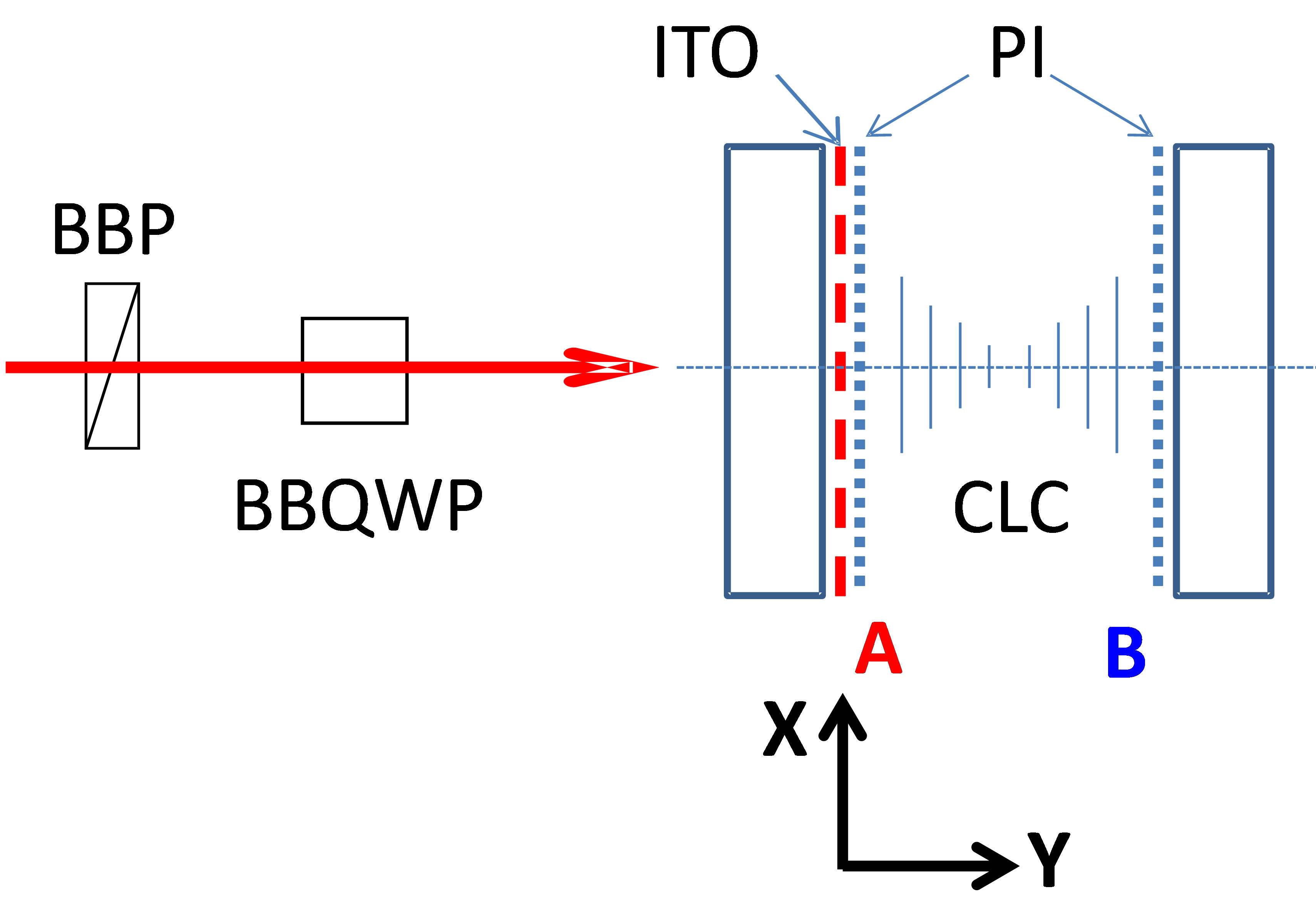
Figure 3. Schematic presentation of the experimental set-up and its key elements: BBP—broad band polarizer, BBQWP— broad band quarter wave plate. The right side of the figure shows the tested asymmetric CLC cell. The surface A contains both the ITO and polyimide layers. The surface B contains only a polyimide layer.
and nav is the local average refractive index of the CLC. Some optical characterization results of mixtures with CB15 are reported in Ref. [15].
The second component (MLC2048) is a nematic liquid crystal (NLC) having a dielectric anisotropy that is positive for “low” frequencies (~1 kHz) and is negative for “high” frequencies (~50 kHz, at room temperature), often called “dual frequency” NLC [16]. The addition of the MLC2048 to the CB15 helps us to tune the pitch and to shift the spectral resonance of the mixture to the NIR spectral band where the reflection of our ITO is more important.
3. Experimental Setup and Results
We started our investigations by polarization dependent transmission measurements by using Varian (Cary 500 scan) spectrophotometer, which can measure light transmission in a broad range. In order to obtain various polarization states of the broadband probe beam (e.g., circularly polarized), we have built a specific setup inside the spectrophotometer (see Figure 3). We used a broad band polarizer (BBP) that transformed the original unpolarized beam into linearly polarized one and a Fresnel rhomb, as broadband quarter wave plate (BBQWP), which generated the circularly polarized probe beam. The polarizer’s axis’ direction was tilted at 45˚ relative to the horizontal (Y, Z) plane (Figure 3) and, when needed, we could turn it to 90˚ to change the circularity handedness (left—right) of the probe beam (after the BBQWP). A second Fresnel rhomb (not shown here) transformed the probe’s polarization back to linear one (if there were no polarization changes in the CLC cell) and also brought its propagation axis into the original one. The CLC cell (with parallel but dissimilar interfaces, see Figure 3) was placed between two BBQWPs, in the area where the probe beam was circularly polarized.
The experimental procedure was the following: we placed the cell of CLC and measured its transmission spectrum; then we turned the cell at 180˚ (with respect to the vertical axis that is parallel to axes X, Figure 3) and we measured the spectrum again (for the opposed direction of propagation of the same probe beam through the same cell). We have repeated this procedure many times for various polarization states of the probe beam and for each position of the cell (cells were also removed and placed back again multiple times to evaluate the contributions of various experimental errors).
The obtained transmission spectra of our cells clearly show non-reciprocal behavior. However, before describeing this behavior, let us remind that the uniform helix of a CLC usually provides a clear resonant reflection band, which is only slightly asymmetric (when going from short to long wavelengths of the resonance) if there are no other causes of losses. In our case, the ITO coating provides strong reflection for the NIR spectra (where the resonance of the CLC is tuned by the addition of the MLC2048), which generates some Fabry-Perrot oscillations. In addition, this ITO introduces significant losses, which grow with the wavelength. That is why, the transmission spectra for our samples is noticeably tilted (decreasing with the increase of wavelength) with FabryPerrot oscillations, Figure 4.
As we have already mentioned, this resonance should be visible only for the circularly polarized light with the same helicicity (as the CLC); while we should observe a relatively flat (uniform) transmission spectra for the opposed circularly polarized light. However, because of above-mentioned reasons, here also the transmission spectra is tilted and contains Fabry-Perrot oscillations Figure 5(a). Most importantly, one can clearly see, from the Figure 5(a), that the transmittance of the cell in the spectral bandgap area is noticeably higher for the case when the left circularly polarized light (which is nonresonant with the CLC) is incident from the side B (see Figure 3). In fact, in our experiments, the non-reciprocity was observed for various states of incident beam’s polarization (including for linear states that are parallel and perpendicular to rubbing direction, etc.) with maximal transmission direction being defined by the type of the polarization. The corresponding results will be detailed in a following full length article [17] (for the sake of the shortness of this communication).
In addition, there was no such effect of non-reciprocity for the same asymmetric cells, which was containing only an NLC (non-chiral) and for all individual elements of used cells (ITO coated glass substrates, etc.). This confirms that the chiral character of CLC layer plays a key role in the observed non-reciprocal transmission effect.
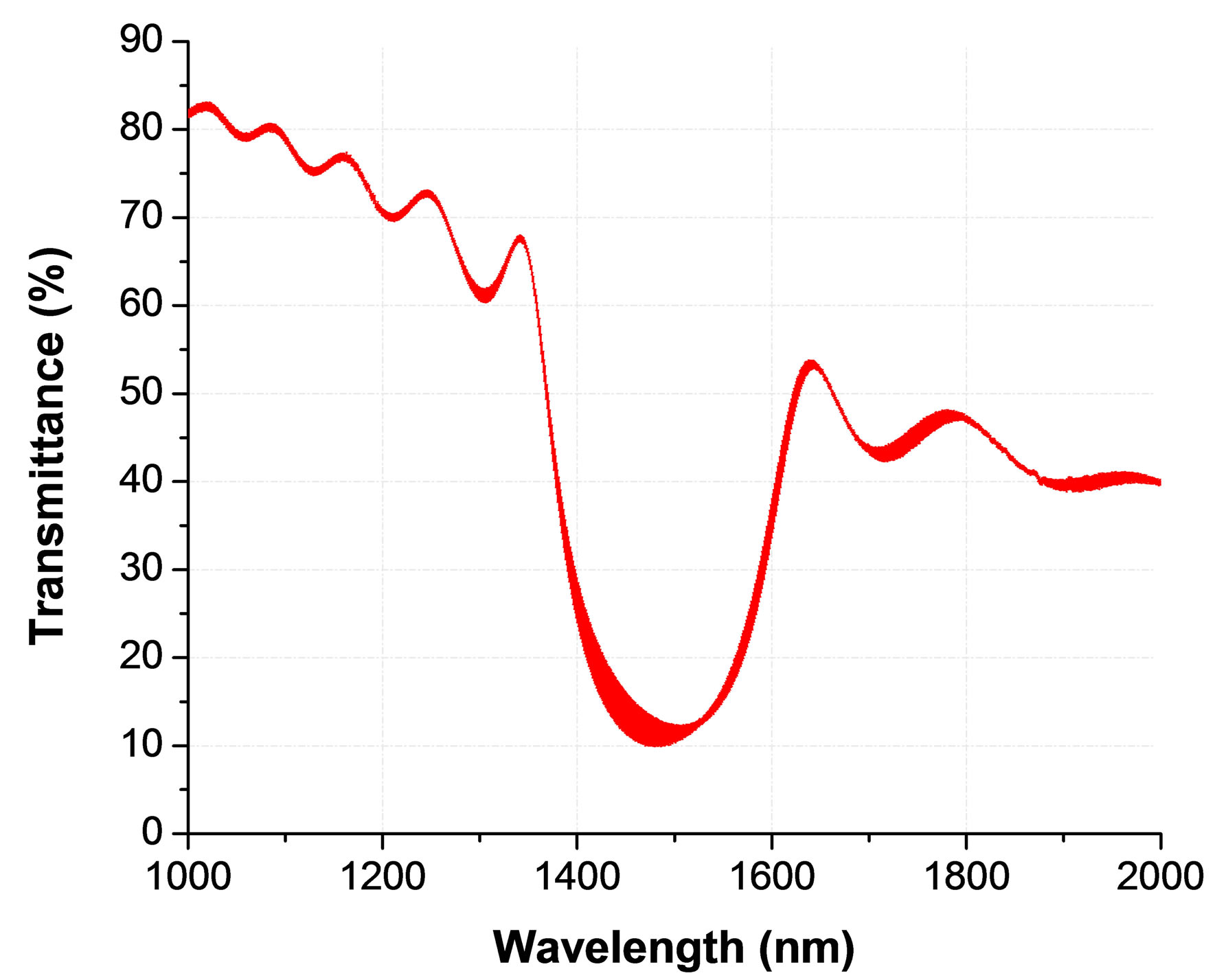
Figure 4. Transmission spectra of the cell for resonantly (right circular) polarized light. Fabry-Perrot oscillations and the spectral tilt are generated due to the high reflection and absorption of the ITO layer for NIR wavelengths.
 (a)
(a) (b)
(b)
Figure 5. Non resonant circularly polarized light transmission spectra (through the same planar cell of CLC) detected for two opposed directions of light propagation (see Figure 3 for the definitions of incidence from the side A & B) for the (a) asymmetric and (b) symmetric optical boundary conditions; from [10].
Finally, the same measurement, performed with the same type of the cell of the same CLC mixture, but containing two ITO coated substrates (and thus with optically symmetric boundary conditions for the CLC layer) shows no such effect (Figure 5(b)). This is emphasizing also the key role of the asymmetric boundary conditions in the observed non-reciprocity. Note that the lower transmission and additional oscillations (seen in Figure 5(b)) are resulted by the presence of the second ITO and the corresponding Fabry-Perrot effect.
4. Discussion
We can theoretically show [10,17], by considering light propagation in a weakly chiral media with asymmetric boundary conditions, that there exist indeed a non-reciprocity of transmission T (by intensity) that may be expressed as 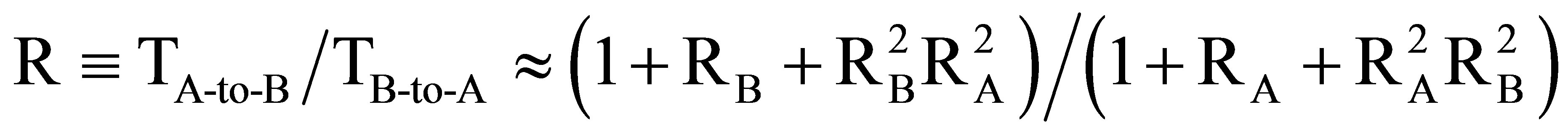 , where RB and RA are reflection coefficients (by intensity) of two opposed surfaces of the CLC. Thus, the difference in reflections RA and RB is necessary for non-reciprocity the theoretical limit of which is R < 2. Also, in the framework of the same theoretical model, we can show that the chiral character of the CLC is necessary for the non-reciprocity, since, otherwise, even if RA ¹ RB, the travel of light in the media will be quite different and the ratio of transmissions in opposed directions will be expressed as
, where RB and RA are reflection coefficients (by intensity) of two opposed surfaces of the CLC. Thus, the difference in reflections RA and RB is necessary for non-reciprocity the theoretical limit of which is R < 2. Also, in the framework of the same theoretical model, we can show that the chiral character of the CLC is necessary for the non-reciprocity, since, otherwise, even if RA ¹ RB, the travel of light in the media will be quite different and the ratio of transmissions in opposed directions will be expressed as 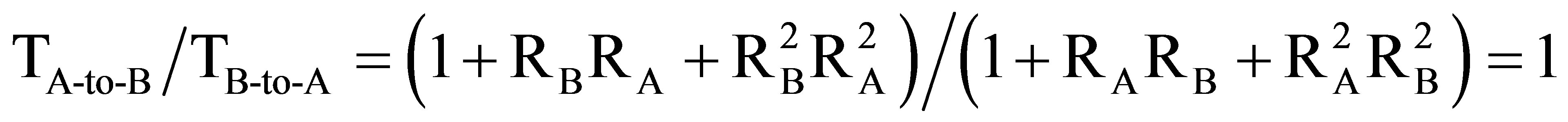 Those two theoretical results confirm our experimental observations, described above.
Those two theoretical results confirm our experimental observations, described above.
Optical non-reciprocity phenomenon was thus demonstrated [10], in a structure that is similar to the cuticle of beetle P. optima, [2]. This non-reciprocity is conditioned by two key parameters of the media: the chirality of the layer and the asymmetry of its boundary conditions. We hope that those observations could stimulate discussions about the role of this non-reciprocity in the evolution of such cuticle structures. While we understand that, at this stage, this is very speculative; we think that the thermal regulation might be one of possible mechanisms driving that evolution. In fact, several works have already been published with analyses of the role of the color in the thermal regulation of beetles. For example, it is known that both black and white colored beetles may co-exist in the Namibian desert, creating thus the so called “black beetle paradox”, see, e.g., Ref. [18] and references therein. It was shown that the direct and reflected visible light illumination of O. bicolor (white) and O. unguicularis (black) beetles may create significant difference of temperature elevation DT in different areas of their body [18]. Thus, the corresponding ratio r = DTblack/DTwhite may achieve values as high as 2.56, 2.22 and 1.89 in beetle’s Thorax, Elytron and Abdomen, respectively [18]. The maximum temperature elevation here could achieve >10˚C, which is rather high if we take into account that the beetle’s body damage may be observed at above 45˚C [18]. However, the combined effect of real life habitat (air temperature in Namibian desert, convection, etc.) is such that the role of the visible light illumination is strongly reduced in those beetles (the wind speed being the most important thermoregulation factor), which apparently have pigment based coloration (we could not find a mention about the iridescence of their color). Thus, as the authors of Ref. [18] mention, while the color does matter to beetle’s thermal energy fluxes, its effect can be modified, obviated and negated in many ways by other environmental conditions. It is also worth mentioning that many species of the iridescent colored beetles are living in the forests of Central America [6] where the environmental conditions and the corresponding influence may be quite different from Namibian desert.
5. Conclusions
The reasons why we raise this question for iridescent colored beetles (such as the P. optima [2]), are several. First, their cuticles reflect light of given helicicity with minimal net absorption and this reflection has highest efficiency in the spectral area of maximum sun power (other wavelengths of sun light also may be diffracted at different angles). We know that the unpolarized sun light may be presented as a sum of two non-coherent polarizations of opposed helicicity (except the scattered one, which may be even plane polarized and thus may also be presented as a sum of two circularly polarized light components). So only the half of sun light may be reflected by the cuticle. Thus, even if the second half of sun power (light with non-resonant polarization helicicity) may still penetrate into this structure, according to our study, its back propagation (evacuation) is significantly favored. The reflection of that second half of sun light could be achieved if the cuticle would contain a second layer of opposed (to the first layer) helicicity. However, while in principle being possible [1], inverting the helicicity of molecules or molecular structures in natural life is an extremely complicated (if possible) process [19] because of the breakdown of chiral symmetry in nature [20]. This might be the reason why the P. resplendens, has developed two layers of the same helicicity with an uniaxial layer in between to transform the non-resonant helicicity of light, passed through the first chiral layer and to make it reflected by the second chiral layer [2], thus always using materials and structures of the same helicicity.
This being said, additional experiments must be conducted on (ideally live) beetles to establish the validity of this hypothesis. Perhaps the monitoring of differential temperature elevation of such beetles in air and in an index matching liquid environment (at least on the cuticle) could bring us closer to the answer. However, the other channels of energy exchange (e.g., air convection) should then be difficult to take into account at the same time [18]. Finally, other aspects of such cuticle formation (structural, deformational, etc.) must be also taken into account to answer this question [1,3,21].
We thank Prof. C. Cloutier, from Laval University, for useful discussions and the Natural Sciences and Engineering Research Council of Canada (NSERC) for their financial support.
REFERENCES
- M. Srinivasarao, “Nano-Optics in the Biological World: Beetles, Butterflies, Birds, and Moths,” Chemical Reviews, Vol. 99, No. 7, 1999, pp. 1935-1961. http://dx.doi.org/10.1021/cr970080y
- S. Caveney, “Cuticle Reflectivity and Optical Activity in Scarab Beetles: The Role of Uric Acid,” Proceedings of the Royal Society of London. Series B, Vol. 178, No. 1051, 1971, pp. 205-225. http://dx.doi.org/10.1098/rspb.1971.0062
- G. Agez, R. Bitar and M. Mitov, “Color Selectivity Lent to a Cholesteric Liquid Crystal by Monitoring InterfaceInduced Deformations,” Soft Matter, Vol. 7, No. 6, 2011, pp. 2841-2847. http://dx.doi.org/10.1039/c0sm00950d
- P. G. de Gennes and J. Prost, “The Physics of Liquid Crystals,” 2nd Edition, Oxford University Press, Oxford, 1995,
- R. B. Alaverdyan, K. R. Allakhverdyan, A. H. Gevorgyan, A. D. Chilingaryan and Y. S. Chilingaryan, “Chiral Photonic Crystals with an Electrically Tunable Anisotropic Defect. Experiment and Theory,” Technical Physics. 2010, Vol. 55, No. 9, pp. 1317-1323.
- D. C. Hawks, “Jewel Scarabs,” Programs Information: Nebraska State Museum, Paper 15, 2002.
- A. T. D. Bennett, I. C. Cuthill and K. J. Norris, “Sexual Selection and the Mismeasure of Color,” American Naturalist, Vol. 144, No. 5, 1994, pp. 848-860. http://dx.doi.org/10.1086/285711
- J. Mappes, N. Marples and J. A. Endler, “The Complex Business of Survival by Aposematism,” TRENDS in Ecology and Evolution, Vol. 20, No. 11, 2005, pp. 598- 603. http://dx.doi.org/10.1016/j.tree.2005.07.011
- T.-H. Chiou, S. Kleinlogel, T. Cronin, R. Caldwell, B. Loeffler, A. Siddiqui, A. Goldizen and J. Marshal, “Circular Polarization Vision in a Stomatopod Crustacean,” Current Biology, Vol. 18, No. 6, 2008, pp. 429-434. http://dx.doi.org/10.1016/j.cub.2008.02.066
- K. Allahverdyan, A. H. Gevorgyan, R. Hakopyan and T. Galstian, “Observation of Optical Non Reciprocity in a Single Layer of Transparent Linear Chiral Media with Asymmetric Boundaries,” JETP Letters, Vol. 96, No. 11, 2012, pp. 694-698. http://dx.doi.org/10.1134/S0021364012230026
- P. Yeh and C. Gu, “Optics of Liquid Crystal Displays,” Wiley, New York, 1999.
- L. M. Blinov and V. G. Chigrinov, “Electrooptic Effects in Liquid Crystal Materials,” Springer, New York, 1994. http://dx.doi.org/10.1007/978-1-4612-2692-5
- K. Takatoh, M. Hasegawa, M. Koden, N. Itoh, R. Hasegawa and M. Sakamoto, “Alignment Technologies and Applications of Liquid Crystal Devices,” Taylor & Francis, London, 2005. http://dx.doi.org/10.1201/9781420023015
- K. Asatryan, V. Presnyakov, A. Tork, A. Zohrabyan, A. Bagramyan and T. Galstian, “Optical Lens with Electrically Variable Focus Using an Optically Hidden Dielectric Structure,” Optics Express, Vol. 18, No. 13, 2010, pp. 13981-13992. http://dx.doi.org/10.1364/OE.18.013981
- K. Allahverdyan and T. Galstian, “Electrooptic Jumps in Natural Helicoidal Photonic Bandgap Structures,” Optics Express, Vol. 19, No. 5, 2011, pp. 4611-4617. http://dx.doi.org/10.1364/OE.19.004611
- Y. Yin, M. Gu, A. B. Golovin, S. V. Shiyanovskii and O. D. Lavrentovich, “Fast Switching Optical Modulators Based on Dual Frequency Nematic Cell,” Molecular Crystals and Liquid Crystals, Vol. 421, No. 1, 2004, pp. 133-144. http://dx.doi.org/10.1080/15421400490501699
- Submitted to the Journal of Physical Review E.
- J. S. Turner and A. T. Lombard, “Body Color and Body Temperature in White and Black Namib Desert Beetles,” Journal of Arid Environments, Vol. 19, No. 3, 1990, pp. 303-315.
- R. Birabassov and T. V. Galstian, “Light-Induced Macroscopic Chirality in Azo-Dye-Doped Polymers,” Journal of the Optical Society of America B, Vol. 18, No. 10, 2001, pp. 1469-1473. http://dx.doi.org/10.1364/JOSAB.18.001469
- B. Norden, “Was the Photo Resolution of Amino Acids the Origin of Optical Activity in Life?” Nature (London), Vol. 266, 1977, pp. 567-568. http://dx.doi.org/10.1038/266567a0
- V. Sharma, M. Crne, J. O. Park and M. Srinivasarao, “Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles,” Science, Vol. 325, No. 5939, 2009, pp. 449-451. http://dx.doi.org/10.1126/science.1172051
NOTES
*Corresponding author.

