Optics and Photonics Journal
Vol.3 No.8A(2013), Article ID:41424,10 pages DOI:10.4236/opj.2013.38A003
Floquet Theory in Electron-Helium Scattering in a Nd:YAG Laser Field
1UFR de Physique du Rayonnement et des Interactions Laser-Matière, Faculté des Sciences, Université Moulay Ismail, Meknès, Morocco
2The Abdus Salam International Centre for Theoretical Physics, Trieste, Italy
3Laboratoire de Chimie Physique-Matière et Rayonnement, Université Pierre et Marie Curie, Paris, France
Email: *makhoute@netcourrier.com
Copyright © 2013 Abdelkader Makhoute et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 27, 2013; revised July 28, 2013; accepted August 25, 2013
Keywords: Laser-Assisted; Elastic Collisions; Born-Approximation; Floquet Theory; Multiphoton Transitions; Low-Lying; High-Lying; Differential Cross Section
ABSTRACT
The dynamics of laser-assisted elastic collisions in helium is studied. The formalism which will be developed to describe such laser-assisted collisions, treats the laser-projectile interaction to all orders, while the electron-helium interaction is treated within the first Born-approximation. Detailed calculations are performed for the elastic scattering of 50 eV electrons by helium accompanied by the transfer of photons. The numerical results show that the good physical interpretation of relevant processes needs to consider the maximum of atomic states.
1. Introduction
Atomic matter exposed to strong radiation fields has become both experimentally and theoretically a broad field of current research. Experimentally, the development of intense and tunable lasers has made possible the observation of multiphoton processes at relatively moderate laser field intensities. The possibility of observing laser-assisted electron impact atomic excitation in the presence of a strong field [1,2], is much more difficult to evidence. In the laser-assisted collisions, dubbed as “Simultaneous Electron-Photon Excitation” (SEPE), the electron-target system can absorb (emit) one or several photons from the laser field, the target atom ending in an excited state. So far, only helium target system and a low frequency field have been considered experimentally: 1) SEPE, in which relatively slow electrons, with incoming energy below the excitation threshold of the metastable 23S state, collide with atoms in their ground state 11S, the laser supplying the needed energy to achieve excitation [REF], 2) SEPE from higher excited states has been also observed [3]. These results raise several questions related to theoretical representation of this class of processes.
The negligeable role of the laser-atom interaction has been investigated by several experiments carried out with low laser field but under conditions where the KrollWatson Approximation (KWA) predicts the vanishing of the free-free cross sections. A very recent study [4] compared KWA results with a R-matrix Floquet calculation of the free-free cross section for 22 eV electrons scattered from helium through angles from 20˚ to 70˚ in a CO2 laser field. The two calculations were both in excellent agreement with experimental data [4]. Most recently, the results of free-free experiments on electron-helium scattering in a Nd:YAG laser field [5] are perfectly consistent with the calculations using the KWA for large scattering angle.
It is known that the laser-assisted electron-atom collisions can be very sensitive to the dressing of the target by the external radiation field [6,7]. There, the formalism which was developed to describe such laser-assisted collisions treated the laser-projectile interaction to all orders, while the laser-target interaction was treated by using first-order time-dependent perturbation theory. This approach is justified for fast incident electrons and when the electric field strength  remains much weaber than the atomic unit of field strength,
remains much weaber than the atomic unit of field strength,  and/or when the laser photon energy is far from being resonant with an atomic transition energy [8,9].
and/or when the laser photon energy is far from being resonant with an atomic transition energy [8,9].
In this paper we describe calculations of differential cross sections for laser-assisted electron-helium collisions in which the interaction between the laser field and the projectile is treated exactly in a non-perturbative way, by using a Volkov wave function [10]. While, the laser-target interaction is treated using the Floquet approach [9,11] for the dominant intermediate state, and perturbatively the remaining target states. Since we are considering fast incident electrons, the interaction between the projectile electron and the target atom is treated using the first Born approximation, and exchange effects are safely neglected [12]. It should be noted that our approach is much less demanding in terms of computational power than the R-Matrix Floquet treatments [4].
In Section 2, we present the theory. In Section 3, laser modifed cross sections and their dependence on laser parameters are discussed, and Section 4 concludes the paper. Atomic units (au) are used throughout this paper.
2. Theoretical Foundation
We consider the collision of fast electrons with atoms in intense laser fields. We assume the laser field to be purly monochromatic, linearly polarized, and spatially homogeneous, thus treated classically and can be written as
 (1)
(1)
where 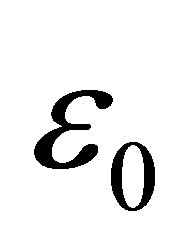 is the field amplitude and
is the field amplitude and  is its polarization vector. The corresponding vector potential is
is its polarization vector. The corresponding vector potential is 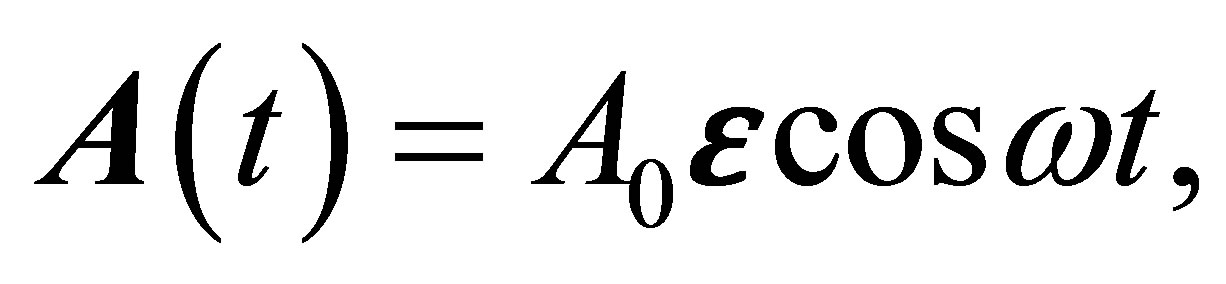 with
with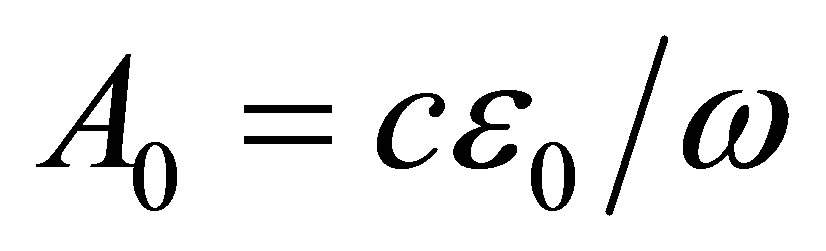 . The wave function of a “free electron interacting with such a field”, is given in the velocity gauge and dipole approximation by the Volkov function
. The wave function of a “free electron interacting with such a field”, is given in the velocity gauge and dipole approximation by the Volkov function
 (2)
(2)
where  is the electron coordinate,
is the electron coordinate,  denotes the its wave vector,
denotes the its wave vector, 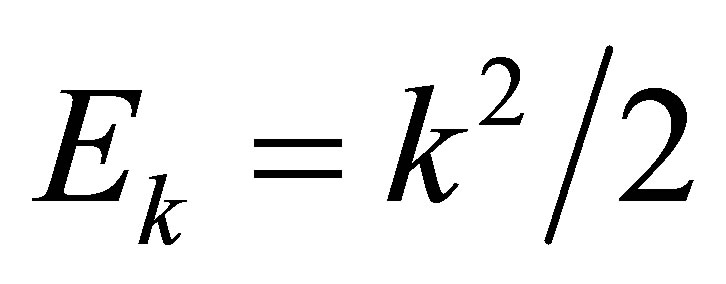 is its kinetic energy and
is its kinetic energy and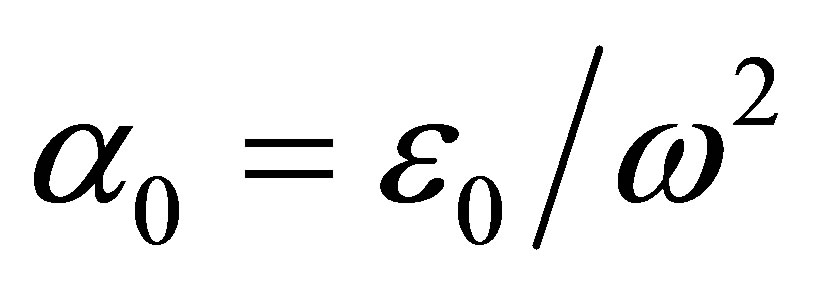 .
.
Our main task consists in obtaining an expression for the “dressed” wave function of the initial and final atomic target states in the laser field, valid to all orders interaction. Therefore, we should solve the time-dependent Schrödinger Equation
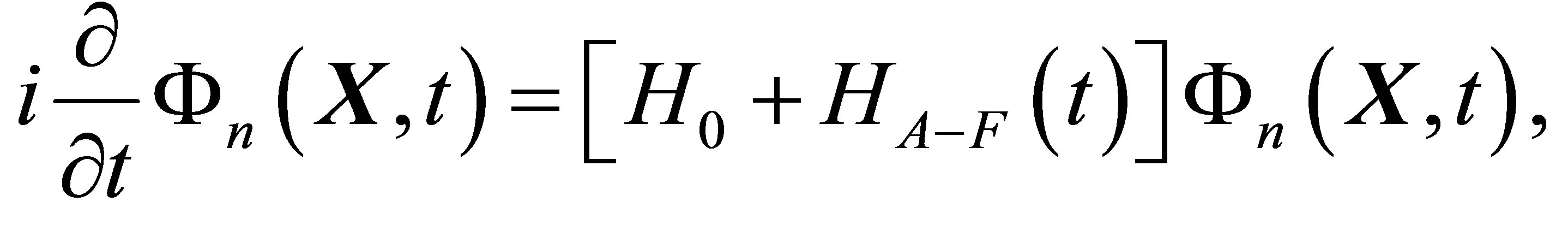 (3)
(3)
where 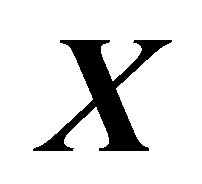 denotes the ensemble of the target electrons coordinates,
denotes the ensemble of the target electrons coordinates, 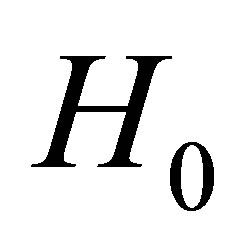 is the target atom Hamiltonian in the absence of the external field and
is the target atom Hamiltonian in the absence of the external field and 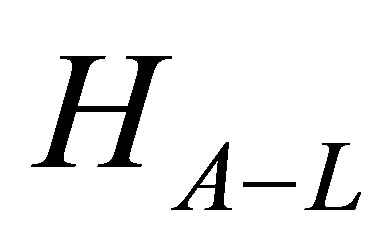 is the atom-field interaction Operator which reads, in the velocity gauge,
is the atom-field interaction Operator which reads, in the velocity gauge,
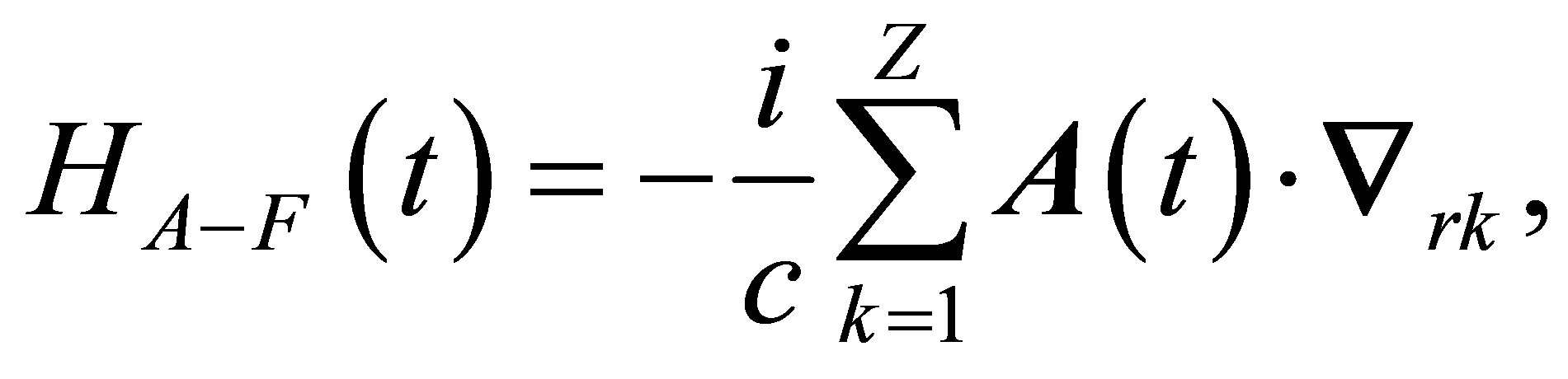
 (4)
(4)
where Z is the atomic number of the target and  is the position vector of the kth target electron.
is the position vector of the kth target electron.
Solving exactly Equation (3) would be a formidable task, but yet hardly achievable.
Therefore, we introduce orthogonal projection operators P, Q such that
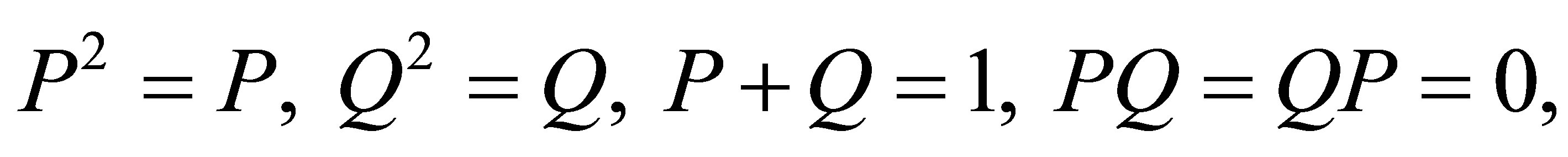 (5)
(5)
where P projects onto the subspace 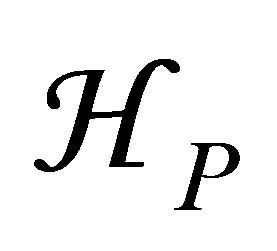 of the states which will be included exactly in the calculation. Note that this subspace should contain the initial and final states of the collision at least.
of the states which will be included exactly in the calculation. Note that this subspace should contain the initial and final states of the collision at least.
The Schrödinger Equation (3) is then approximated, in a first stage, by the simplified Equation
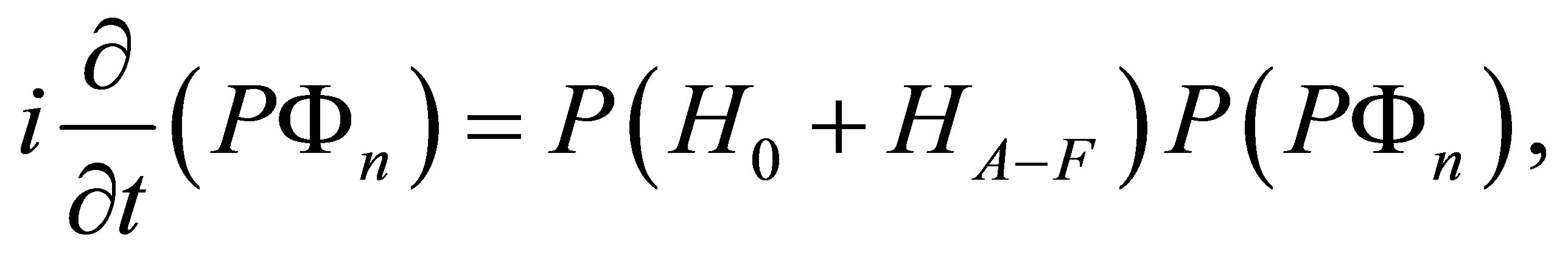 (6)
(6)
in which only the few dominant states are coupled. Using the usual Floquet ansatz [9,13] we seek solutions of the form
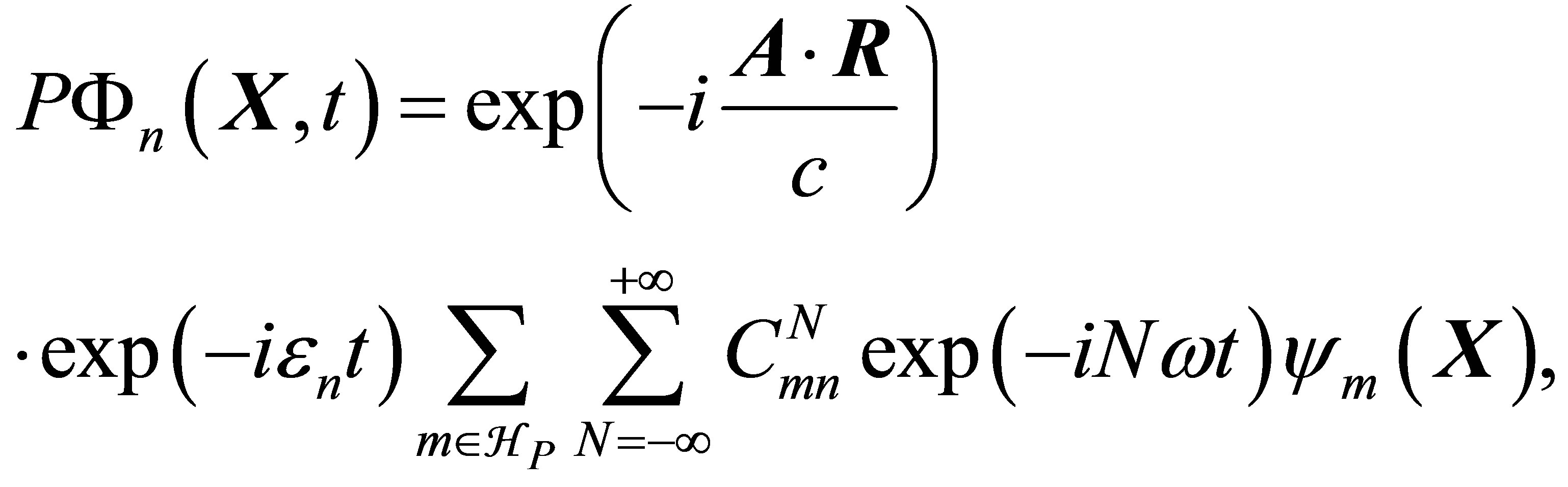 (7)
(7)
where we have defined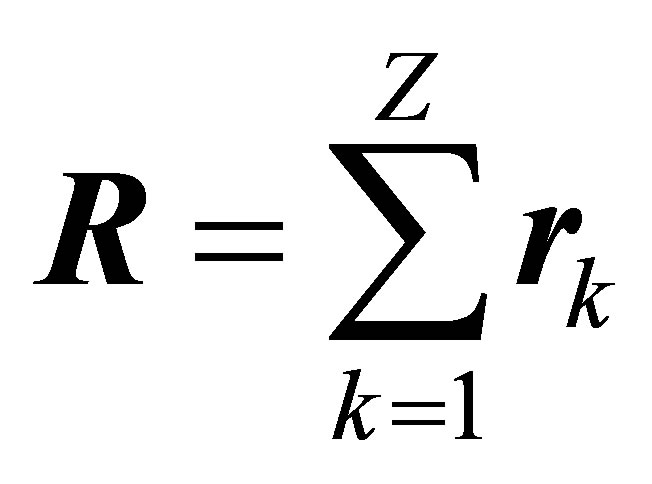 , and
, and 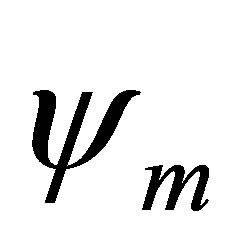 is a target state of energy Em in the absence of the external field. The Floquet coefficients
is a target state of energy Em in the absence of the external field. The Floquet coefficients 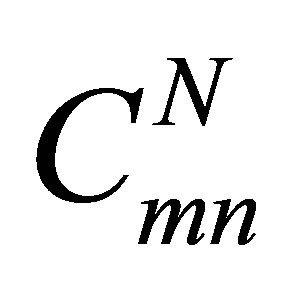 and the pseudo-energies
and the pseudo-energies  can be found by solving numerically the eigenvalue problem
can be found by solving numerically the eigenvalue problem
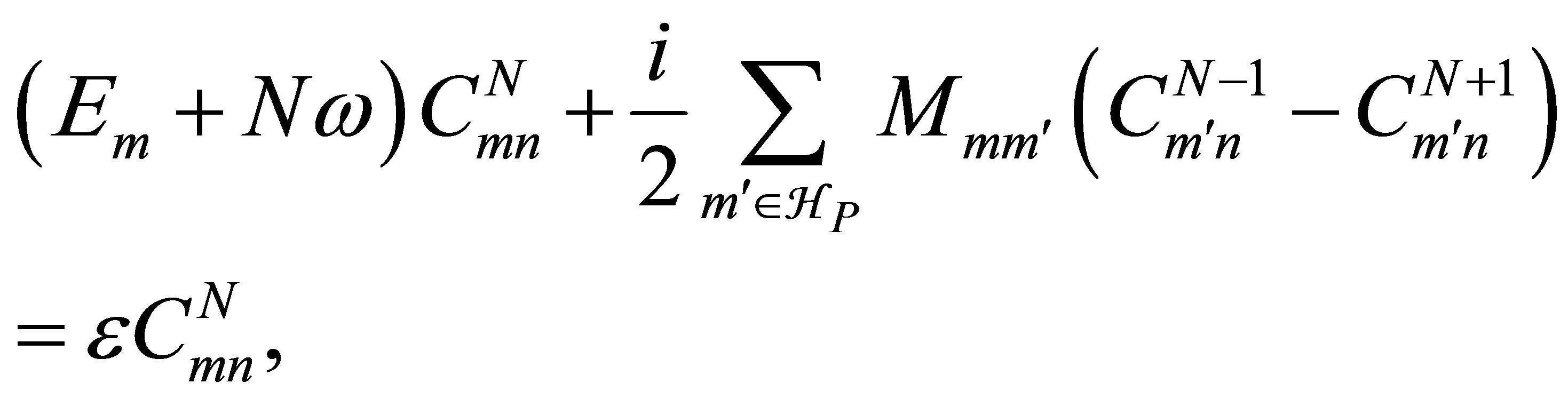 (8)
(8)
where we have introduced the dipole-coupling matrix elements
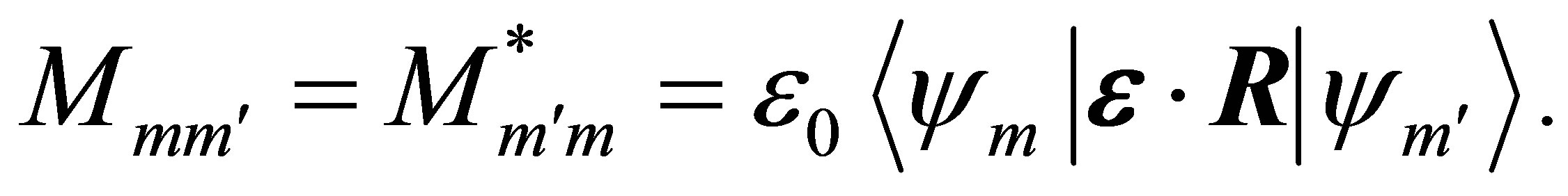 (9)
(9)
Finally, a first-order correction to the approximate wave function 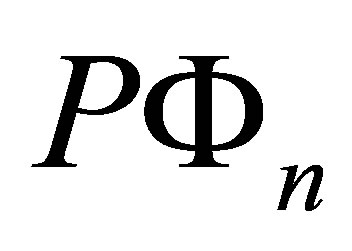 can be found by treating perturbatively the coupling to all the states which are not included in the subspace
can be found by treating perturbatively the coupling to all the states which are not included in the subspace 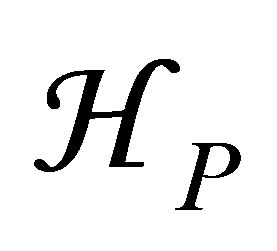 (the states of
(the states of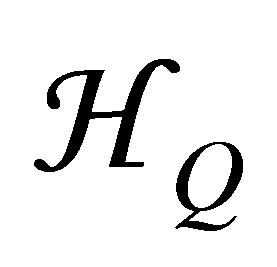 ) and “switching on” the interaction in an adiabatic way. We obtain
) and “switching on” the interaction in an adiabatic way. We obtain
 (10)
(10)
where the first-order approximation to 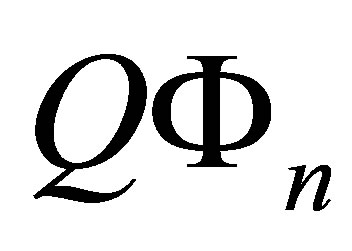 is a solution of the Equation
is a solution of the Equation
 (11)
(11)
Explicitly, we have
 (12)
(12)
In the last Equation the summation over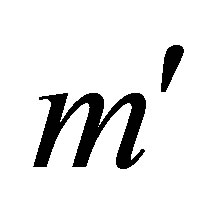 , where
, where 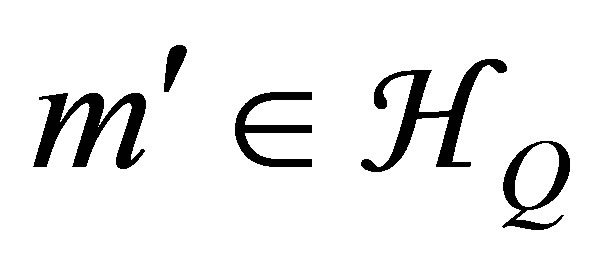 includes an integration over the continuum states. We remark that the solution (12) is valid for any laser frequencies values, therefore the laser photon energy could be close to the energy of an atomic transition between the initial or final states and an intermediate state of the collision process. In what follows we will denote by
includes an integration over the continuum states. We remark that the solution (12) is valid for any laser frequencies values, therefore the laser photon energy could be close to the energy of an atomic transition between the initial or final states and an intermediate state of the collision process. In what follows we will denote by  and
and  the dressed initial and final states, respectively.
the dressed initial and final states, respectively.
It should be noted that since the Floquet pseudoenergies 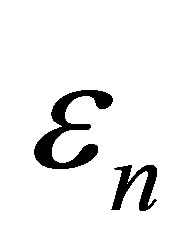 are only defined modulo the photon energy, the Floquet pseudostates are not unique. Our convention will be to define
are only defined modulo the photon energy, the Floquet pseudostates are not unique. Our convention will be to define  as the pseudostate whose pseudoenergie
as the pseudostate whose pseudoenergie 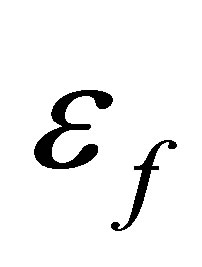 tends to the unperturbed eigenenergie Ef in the limit
tends to the unperturbed eigenenergie Ef in the limit .
.
The S-matrix element for elastic scattering from the ground state, in the direct channel, in the presence of the laser field and in first Born approximation is then given by
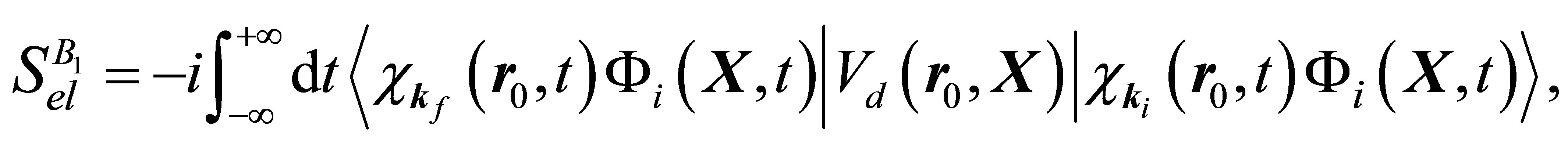 (13)
(13)
where
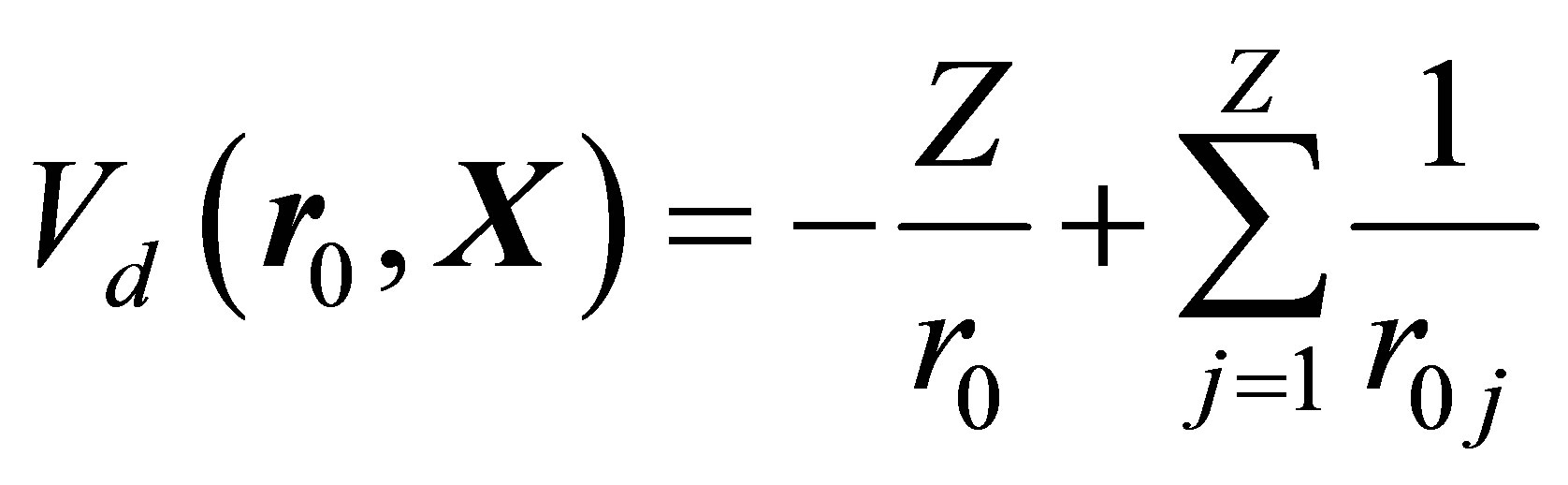 (14)
(14)
is the electron-target interaction operator.
The time integration is readily performed and leads to an energy-conservation delta function.
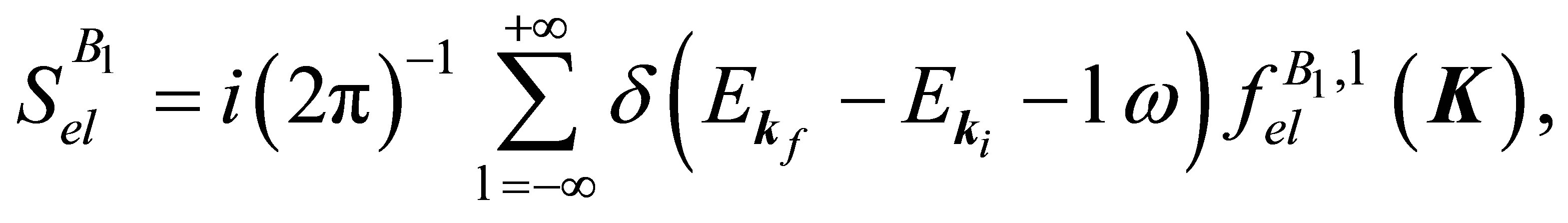 (15)
(15)
where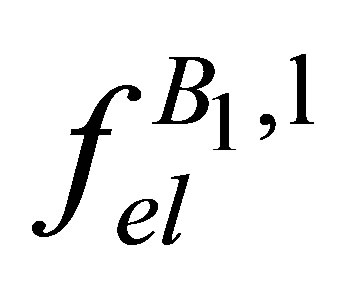 , the first Born approximation to the scattering amplitude with the transfer of ℓ photons can be written as
, the first Born approximation to the scattering amplitude with the transfer of ℓ photons can be written as
 (16)
(16)
with
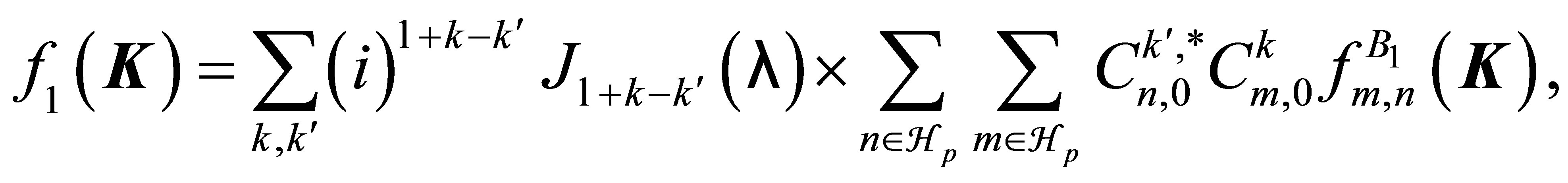 (17)
(17)
 (18)
(18)
and
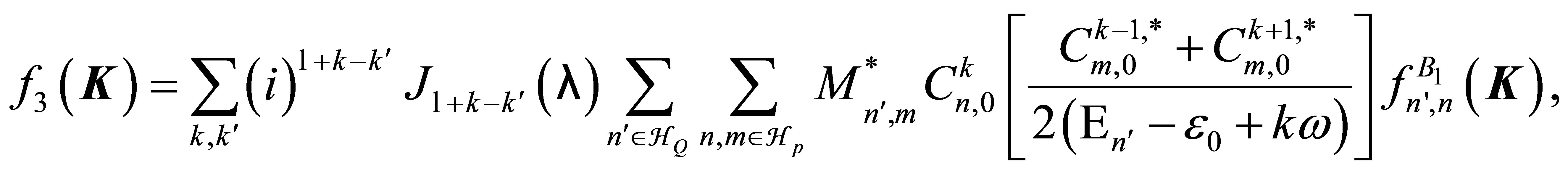 (19)
(19)
In this formula  is the momentum transfer,
is the momentum transfer, 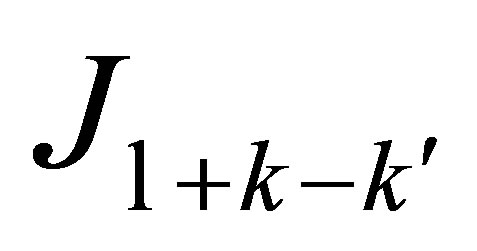 is an ordinary Bessel function of order
is an ordinary Bessel function of order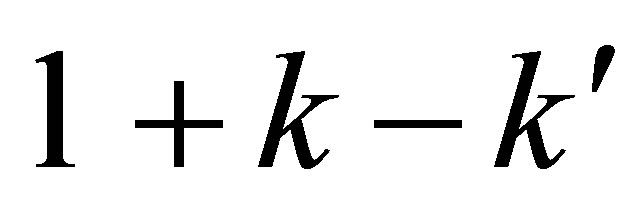 ,
,  and we have defined the matrix elements,
and we have defined the matrix elements,
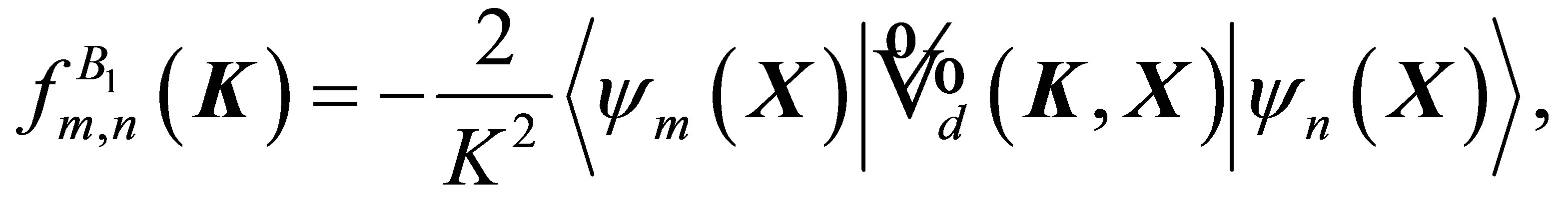 (20)
(20)
This quantity represents the first Born amplitudes corresponding to the scattering event , in the absence of the external field.
, in the absence of the external field.
The operator 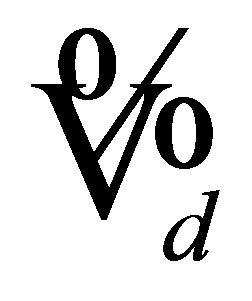 is given by
is given by
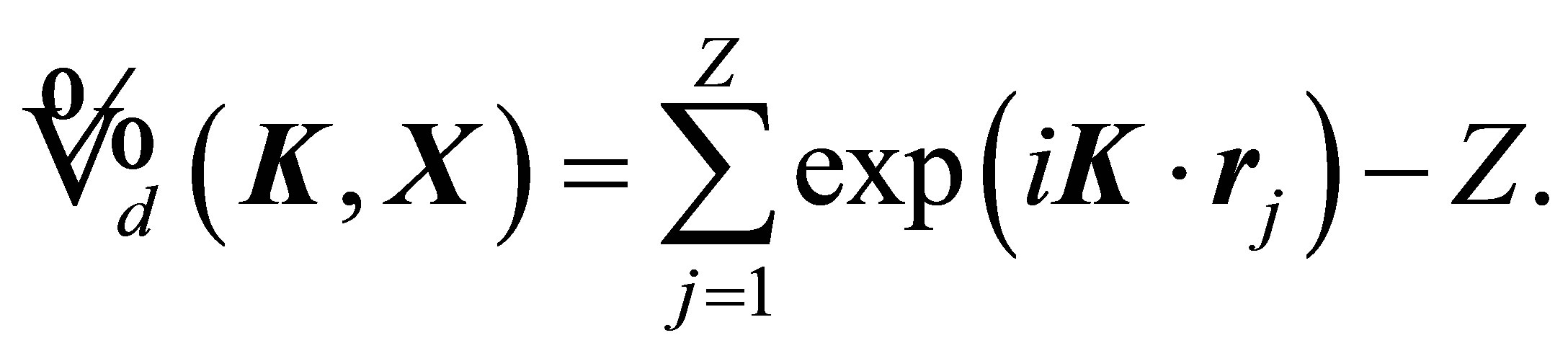 (21)
(21)
using the well known Bethe formula [14]
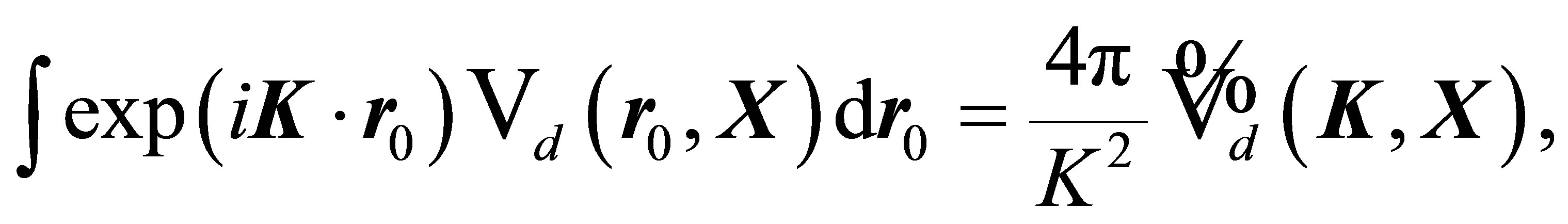 (22)
(22)
The first Born differential cross section corresponding to the various multiphoton processes is given by
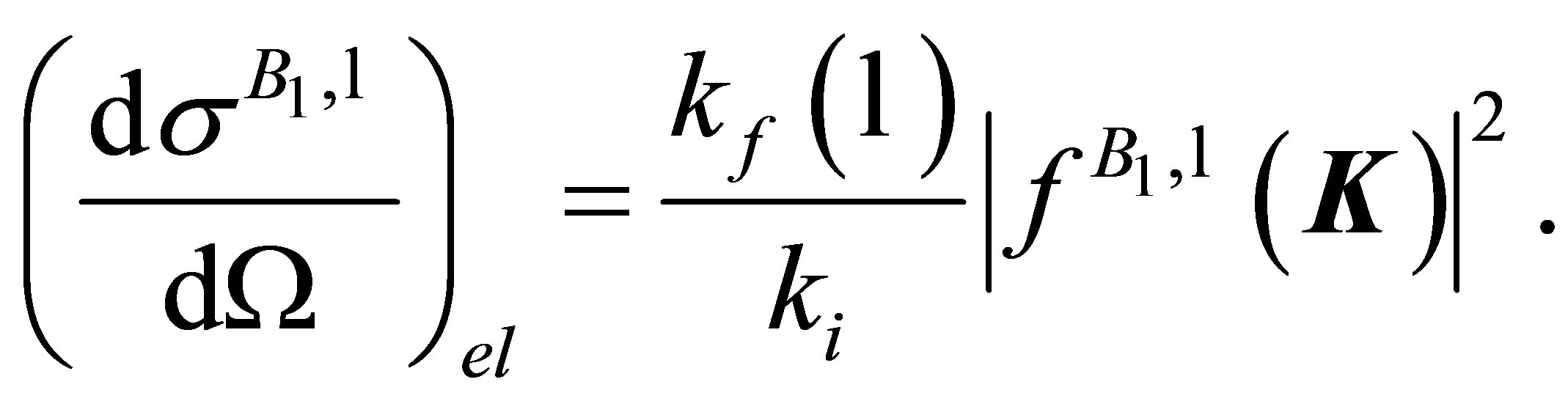 (23)
(23)
In Equation (16), the first term f1, corresponds to the interaction of the laser field with the atomic system in the subspace HP. By retaining only this term, we find that the first Born differential cross section corresponding to the elastic scattering, which is nonperturbative in the subspace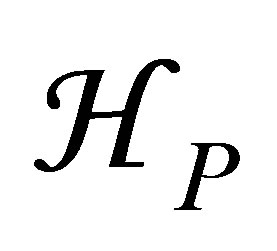 . with the transfer of ℓ photons is given by
. with the transfer of ℓ photons is given by
 (24)
(24)
The amplitudes f2 and f3 contain infinite sums running over the whole atomic spectrum, and the complement of the HP states by those HQ with the transfer of ℓ laser photons. These amplitudes have been accurately computed with the help of time-dependent perturbation theory.
An exact evaluation of Equations (18) and (19) is not possible since no general, accurate wave functions are known for all excited states of helium. On the other hand, although the closure approximation could be used to evaluate the terms contained in the summation over , when
, when  is in the subspace
is in the subspace . We can approximate the “exact” first Born scattering amplitude given by (18) and (19) by including exactly the intermediate states which contribute significantly to the sum, while using the closure approximation to account for the other states. This yields the following approximation for the scattering amplitudes
. We can approximate the “exact” first Born scattering amplitude given by (18) and (19) by including exactly the intermediate states which contribute significantly to the sum, while using the closure approximation to account for the other states. This yields the following approximation for the scattering amplitudes
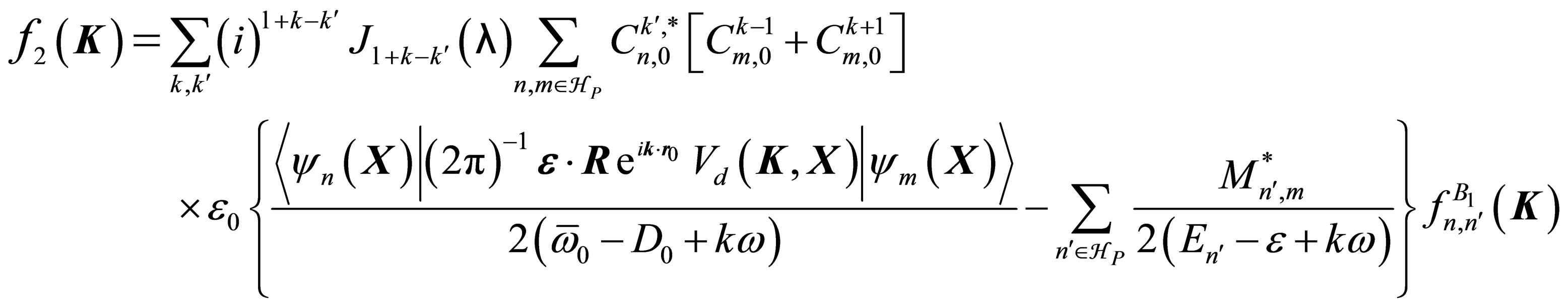 (25)
(25)
and
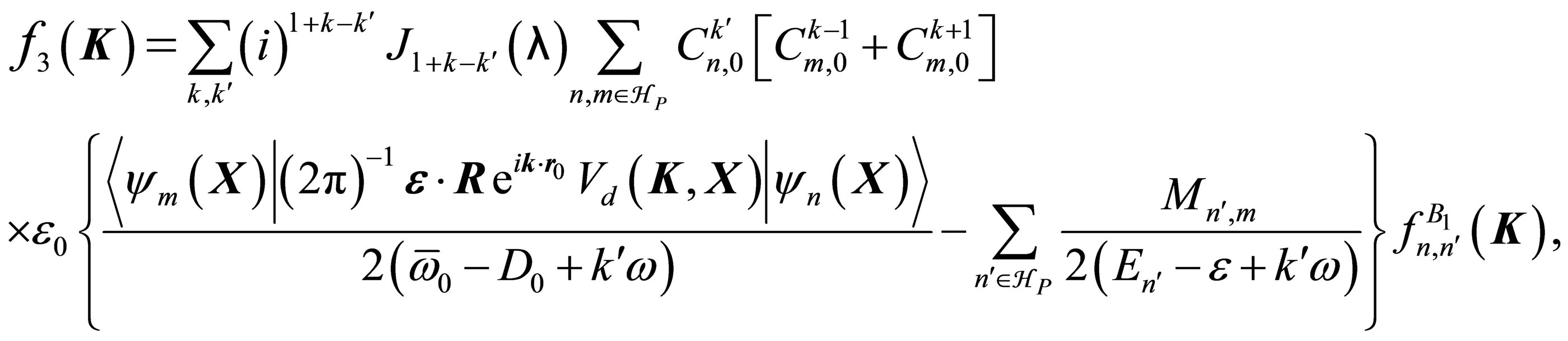 (26)
(26)
where ,
, 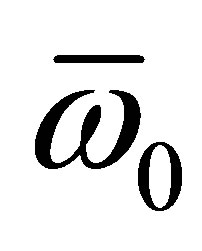 is the average difference between the energy of intermediate state that of the ground state (i.e. the average excitation energy). For
is the average difference between the energy of intermediate state that of the ground state (i.e. the average excitation energy). For 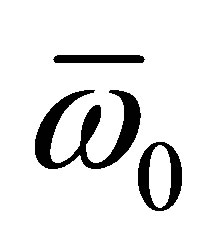 we have chosen the value 1.15 a.u., which gives the correct dipole polarizability of the helium ground, state
we have chosen the value 1.15 a.u., which gives the correct dipole polarizability of the helium ground, state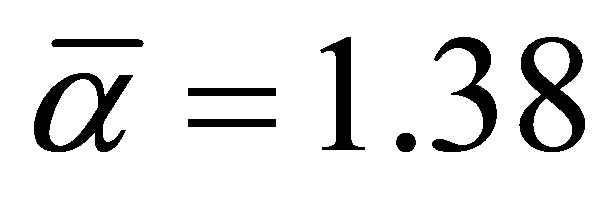 . In writing down Equations (25) and (26), we have only considered the case of final and intermediate states in the subspace
. In writing down Equations (25) and (26), we have only considered the case of final and intermediate states in the subspace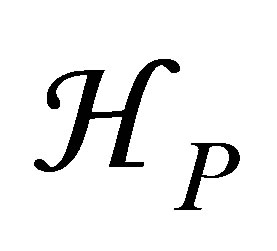 , since exchange effects (which are small at high energies) are not included in our treatment. The sum over
, since exchange effects (which are small at high energies) are not included in our treatment. The sum over 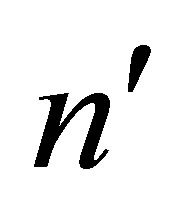 appearing in Equations (25) and (26) now involves only those intermediate states which we treat exactly.
appearing in Equations (25) and (26) now involves only those intermediate states which we treat exactly.
For the ground state we use the wave function [9]
 (27)
(27)
where the orbital 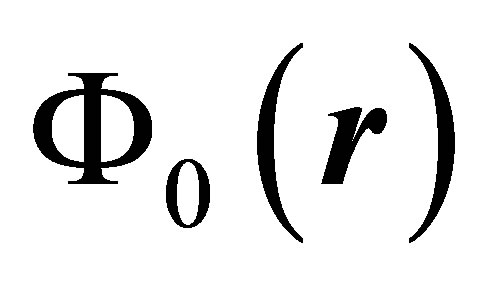 is given by
is given by
 (28)
(28)
with A = 2.60505, B = 2.08144, α = 1.41 and 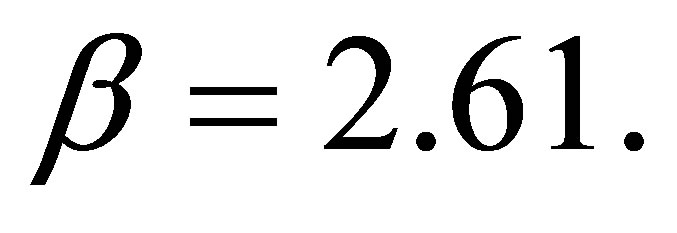 For the 21S state we have chosen the wave function [9,15]
For the 21S state we have chosen the wave function [9,15]
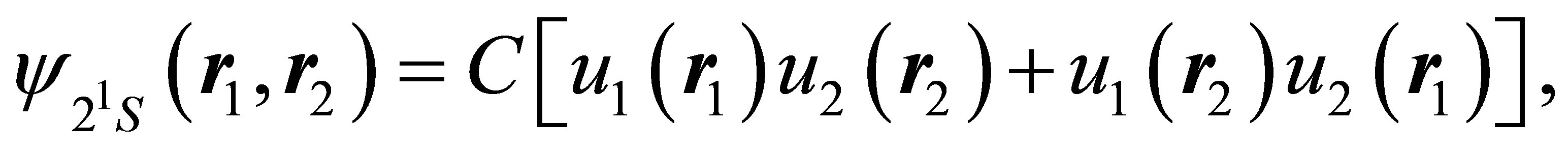 (29)
(29)
where
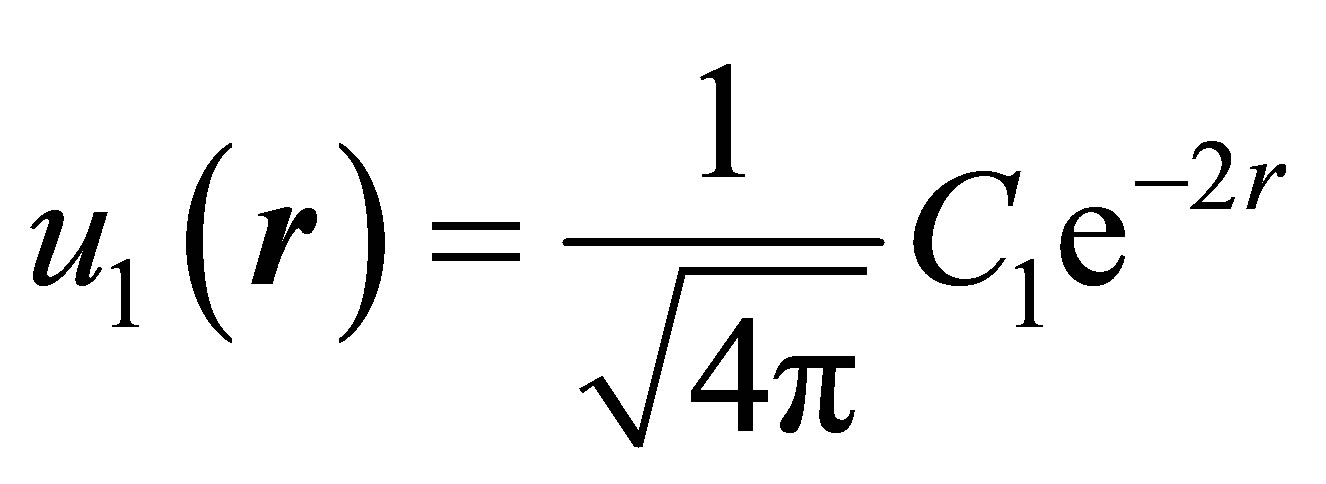 (30)
(30)
and
 (31)
(31)
The values of the parameters being C = 0.705226, C1 = 5.656854, C2 = 0.619280, τ1 = 0.865, τ2 = 0.522 and S = 0.432785.
The intermediate states 21P and 31P, are represented by expressions of the form
 (32)
(32)
where 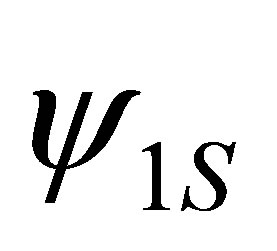 and
and 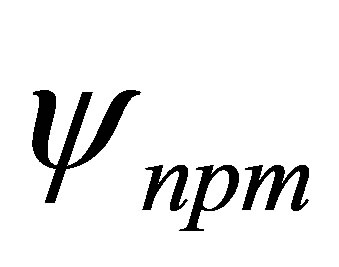 are hydrogenic wave function corresponding to 1s and npm states with effective charges Zi = 2 and Z0 = 1, respectively, and the index n can be take both the values 2 and. Since we want to include exactly all intermediate states with principal quantum number n ≤ 3, we also need in the present case the wave functions of the 31S and 31D states. For the 31S state we have used the function [9,15]
are hydrogenic wave function corresponding to 1s and npm states with effective charges Zi = 2 and Z0 = 1, respectively, and the index n can be take both the values 2 and. Since we want to include exactly all intermediate states with principal quantum number n ≤ 3, we also need in the present case the wave functions of the 31S and 31D states. For the 31S state we have used the function [9,15]
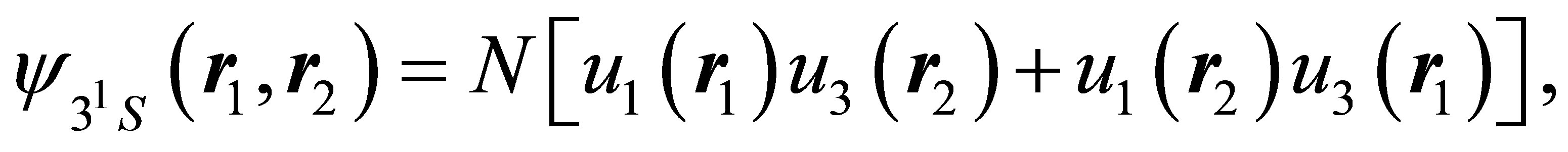 (33)
(33)
where 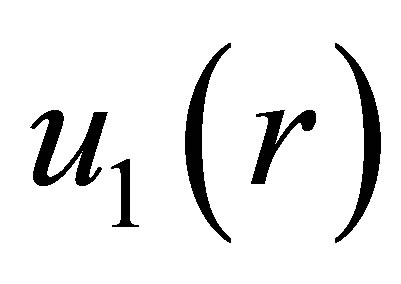 is given by (41),
is given by (41),
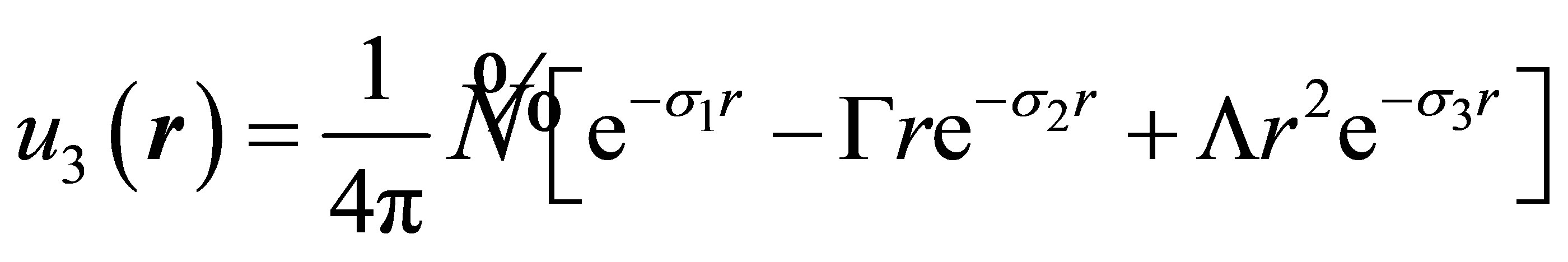 (34)
(34)
and the values of the parameters are N = 0.512410, 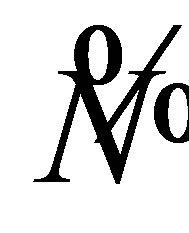 = 0.456615, σ1 = 0.331, σ2 = 0.464, σ3 = 0.330, Γ = 0.932435, and Λ = 0.0038820. This function is orthogonal to the 11S wave function (27) and the 21S wave function (29), and gives the accurate value −2.0606 a.u. for the energy of the 31S state. For the 31D state, we have used a wave function of the type [9,15]
= 0.456615, σ1 = 0.331, σ2 = 0.464, σ3 = 0.330, Γ = 0.932435, and Λ = 0.0038820. This function is orthogonal to the 11S wave function (27) and the 21S wave function (29), and gives the accurate value −2.0606 a.u. for the energy of the 31S state. For the 31D state, we have used a wave function of the type [9,15]
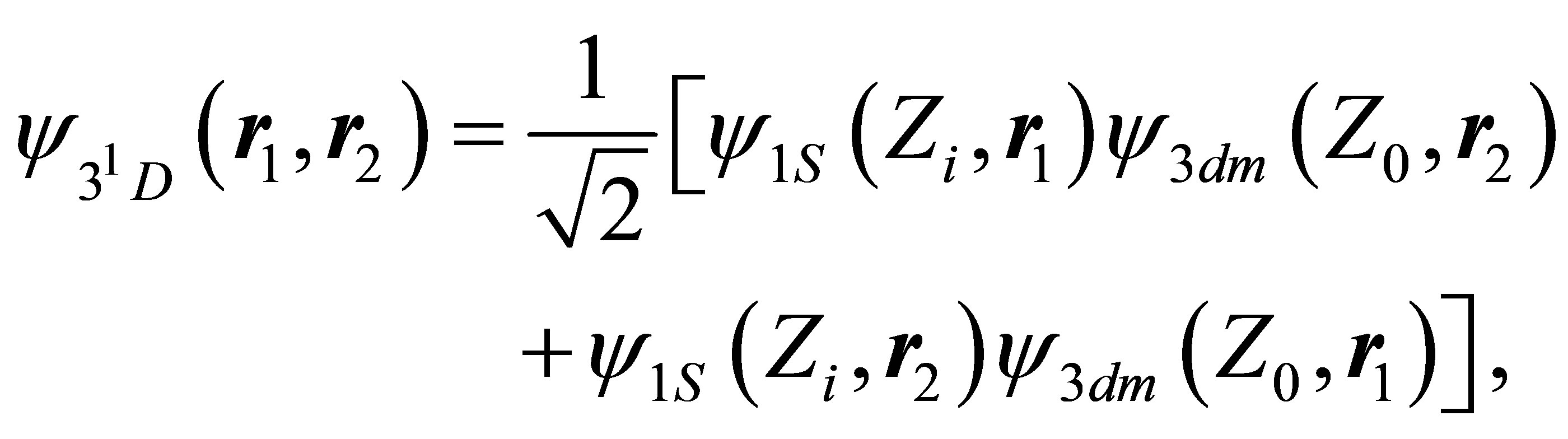 (35)
(35)
where 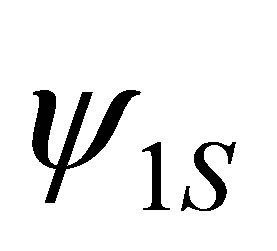 and
and  are hydrogenic wave function corresponding to the effective charges Zi = 2 and Z0 = 1, respectively.
are hydrogenic wave function corresponding to the effective charges Zi = 2 and Z0 = 1, respectively.
3. Results and Discussion
We will discuss the variation of the cross-sections corresponding to the elastic collisions in terms of the parameters governing the collision dynamics, i.e., the scattering angle and number of photons exchanged during the collision. We will also discuss the influence of the laser polarization on the processes, which plays a purely geometrical role. In particular it can give rise to a strong asymmetry between absorption and emission. Our results refer to an incident electron energy 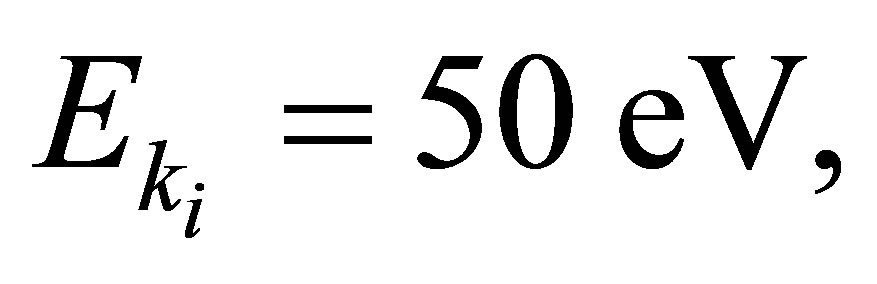 a fixed Nd:YAG laser photon energy
a fixed Nd:YAG laser photon energy 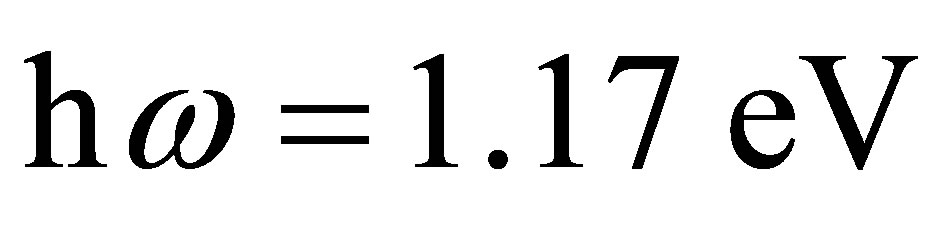 and typical electric field strengths
and typical electric field strengths  Moreover, we have considered here three particular geometries where the polarization vector of the field is taken to be parallel to the momentum transfer
Moreover, we have considered here three particular geometries where the polarization vector of the field is taken to be parallel to the momentum transfer , or to be parallel to the momentum of the incident electron
, or to be parallel to the momentum of the incident electron 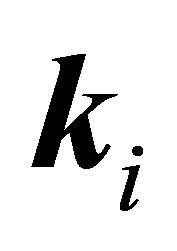 and or to be perpendicular to the incident momentum.
and or to be perpendicular to the incident momentum.
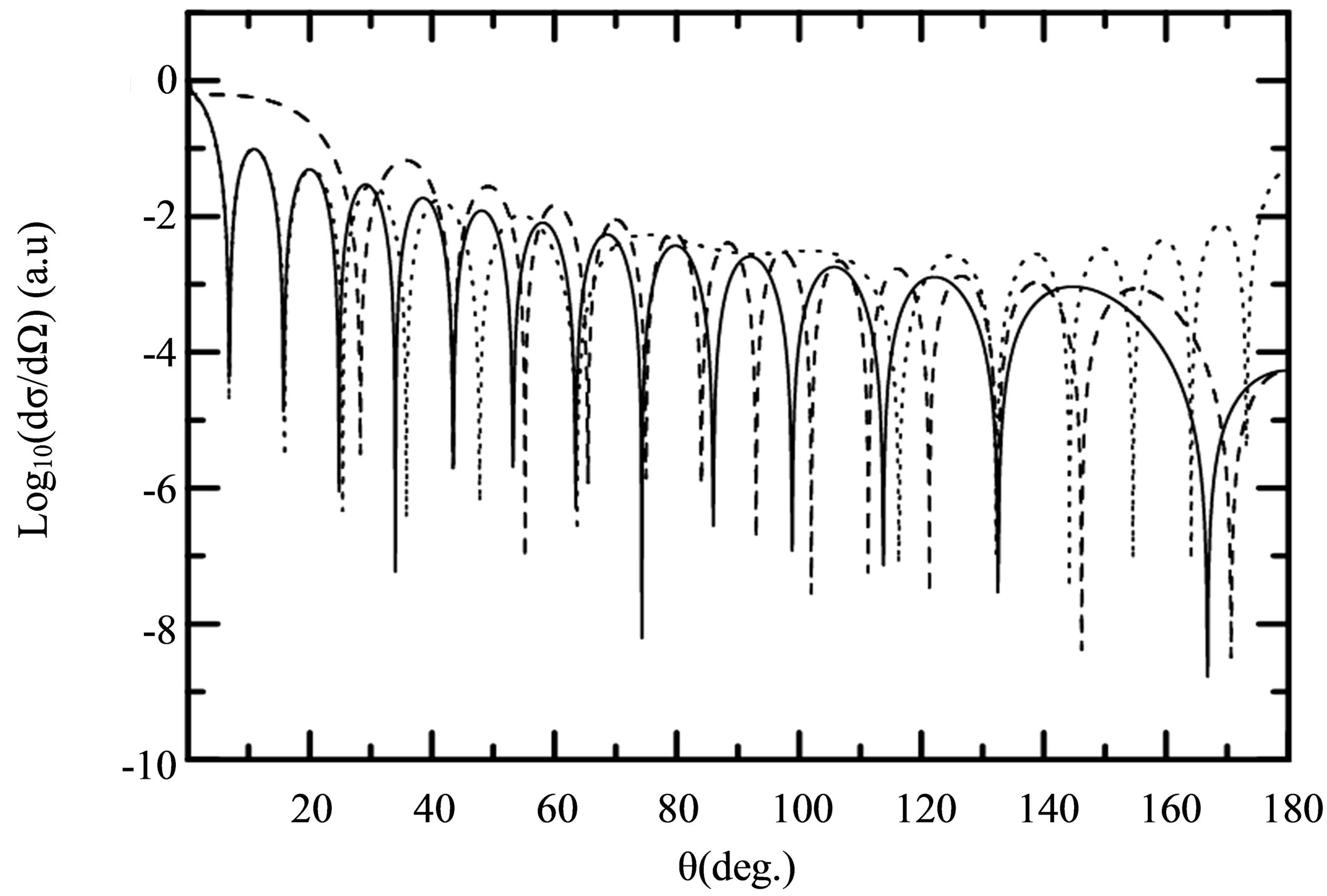
In Figure 1, we display the differential cross section accompanying ℓ = 0, +1 photons exchanged between the electron-atom system and the radiation field. We presente the effects of the states which are not included in the subspace HP by comparing the results obtained from Equation (23) (in which only the dominant states are coupled) and Equation (24) (which can be found by treating perturbatively the coupling to all the states which are note included in the subspace HP) in the same graph for different geometries.
Our results are interpreted by considering the firstBorn differential cross sections, for a fixed electric field strength and a fixed laser photon energy. We have examined our treatment in first Born approximation as a function of the scattering angles and they give similar results beyond 50eV for the incoming electron energies. For the scattering without any net exchange of photons the differences between the results obtained from Equation (23) and those obtained from Equation (24) are too small to be seen on the scale of Figure 1 and can be neglected. In contrast, for the net exchange of one photon, the differences are very important at small scattering angles and are otherwise constant for a given incident energy and a fixed ℓ for different geometries. This is due to the presence the states which are not included in the subspace HP. For a calculation valid to all orders in the interaction between the radiation field and the atomic states of the collision, and for a good physical interpretation of the results requires to consider the maximum atomic states.
In Figure 2 we display the differential cross-section accompanying ℓ = 0, ±1, ±2 photons exchanged for three distinct geometries for the laser polarization vector  either parallel or perpendicular to the incident momentum
either parallel or perpendicular to the incident momentum 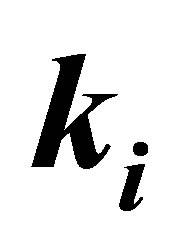 and parallel to momentum transfer
and parallel to momentum transfer .
.
The results displayed in the set of Figure 2 correspond to the complete results obtained by using the scattering amplitude (16) for three different geometries. The features of these graphs are more or less the same. Each cross-section oscillates by a few orders over the whole scattering angular range. However, there is a significant difference between the results of three geometries in each graph: the cross-section for a parallel geometry oscillate more frequently in the intermediate angles, and its envelop (not drown in each graph) declines with scattering angle increasing; in contrast, the results for a perpendicular geometry oscillate more frequently at the forward and backward angles, and its envelop (not present in each graph) rise after θ = 90˚. While for the case in which the polarization vector  of the field is parallel to the momentum transfer
of the field is parallel to the momentum transfer , the cross section oscillate more frequently at the forward angles and its envelop declines with scattering angle increasing. The Bessel function
, the cross section oscillate more frequently at the forward angles and its envelop declines with scattering angle increasing. The Bessel function 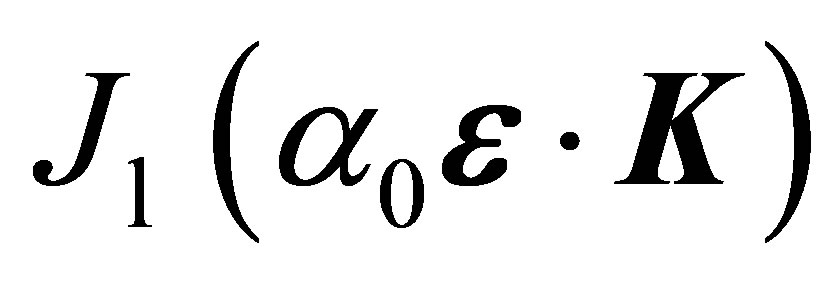 appearing in the direct amplitudes of Equations (17)-(19) are responsible for the cross-section oscillations. For a parallel polarization geometry, the argument of Bessel unction changes slowly against the scattering angle in the forward and backward direction, which cause the cross-sections oscillating slowly; in medium angular range the argument varies rapidly, and leads to the rapid oscillation of cross-section at mediate angles. For a perpendicular polarization geometry, the situation is opposite: the argument of Bessel functions varies rapidly at small and large angles, but slowly at intermediate angles, thus leads to the opposite feature in the perpendicularly polarized cross-sections. For the geometry where the polarization vector of the field is taken to be parallel to the momentum transfer
appearing in the direct amplitudes of Equations (17)-(19) are responsible for the cross-section oscillations. For a parallel polarization geometry, the argument of Bessel unction changes slowly against the scattering angle in the forward and backward direction, which cause the cross-sections oscillating slowly; in medium angular range the argument varies rapidly, and leads to the rapid oscillation of cross-section at mediate angles. For a perpendicular polarization geometry, the situation is opposite: the argument of Bessel functions varies rapidly at small and large angles, but slowly at intermediate angles, thus leads to the opposite feature in the perpendicularly polarized cross-sections. For the geometry where the polarization vector of the field is taken to be parallel to the momentum transfer , the argument of the Bessel function being then reduced to an identical value
, the argument of the Bessel function being then reduced to an identical value , which varies in the same sense as scattering angle. This causes the cross sections oscillating declines with scattering angle increasing.
, which varies in the same sense as scattering angle. This causes the cross sections oscillating declines with scattering angle increasing.
In the case of elastic collisions, dressing effects to be dominant in the forward direction for a given laser photon energy. This behavior is illustrated in the set of Figure 3, where we present the differential cross-sections for laser-assisted scattering with the net exchange of one photon (ℓ = ±1) as a function of the scattering angle θ and for three distinct polarizations of the field (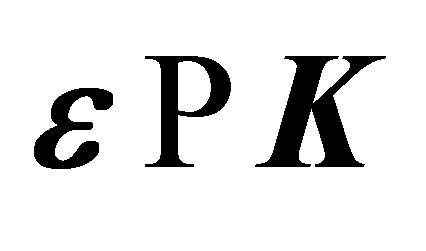 ,
, and
and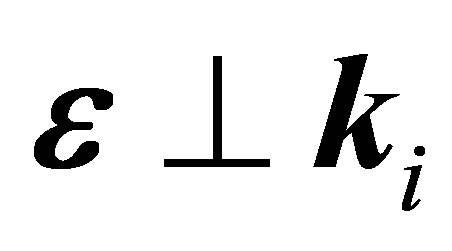 ). The complete results obtained by using amplitude (24) is compared to the cross section obtained by using first-order time-dependent perturbation
). The complete results obtained by using amplitude (24) is compared to the cross section obtained by using first-order time-dependent perturbation
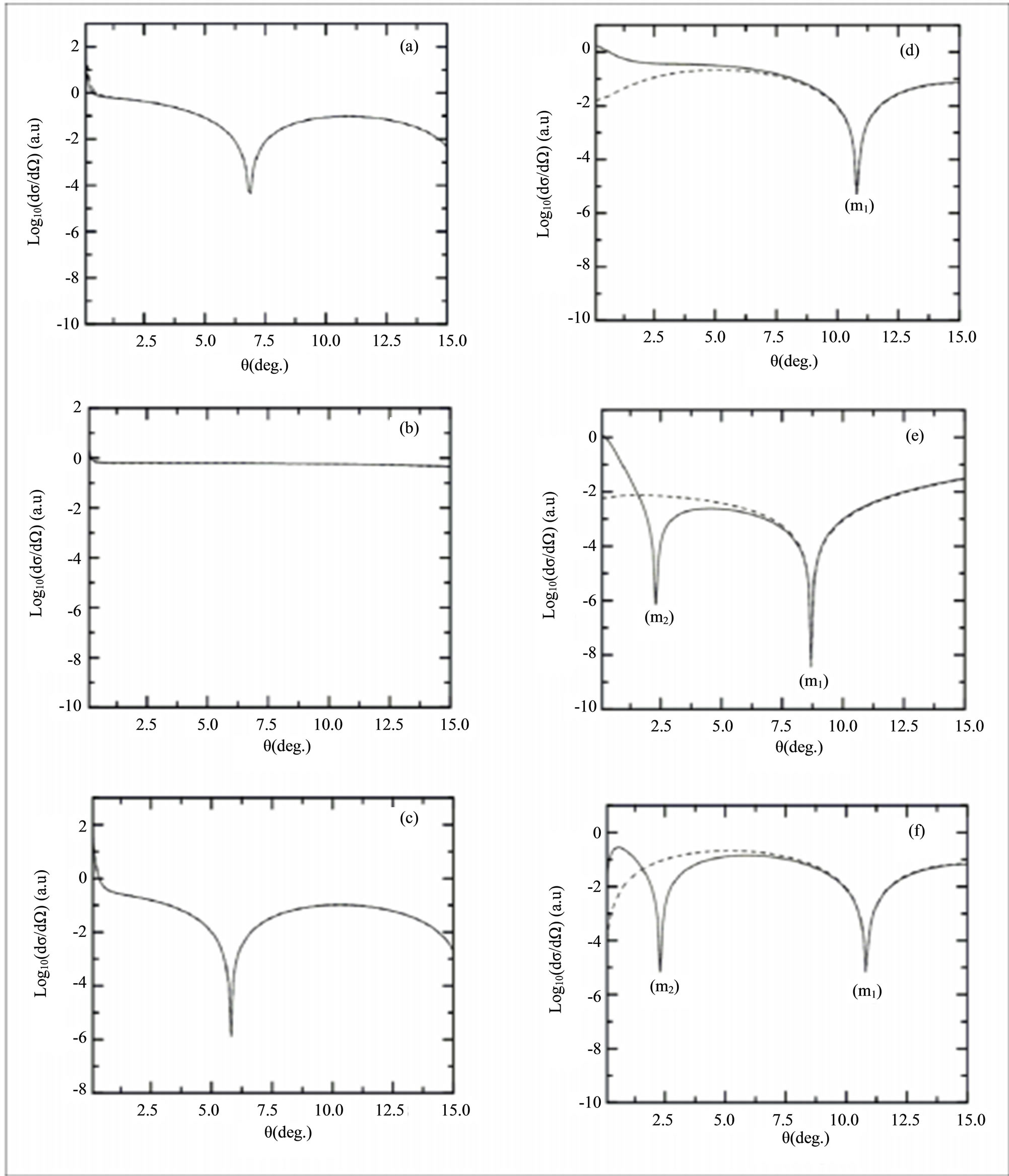
Figure 1. Variation of 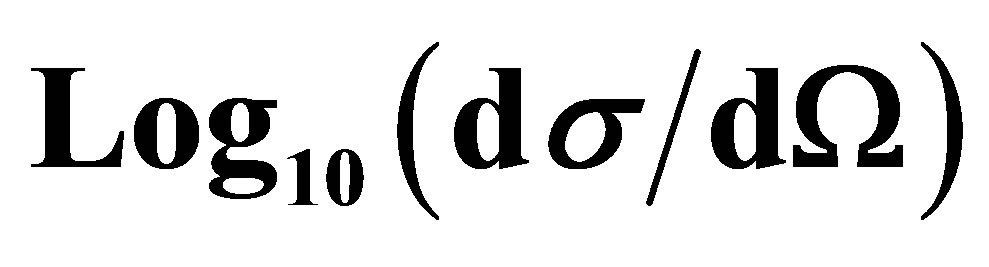 as function of the scattering angle θ. The incident electron energy is
as function of the scattering angle θ. The incident electron energy is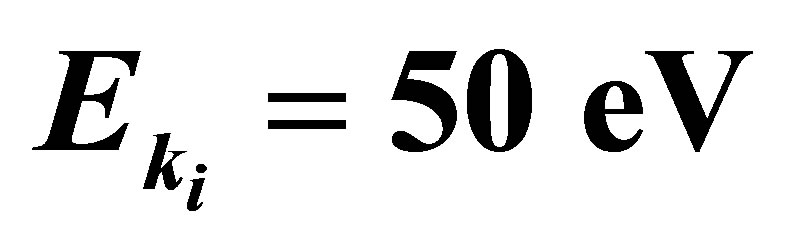 , the laser photon energy is
, the laser photon energy is 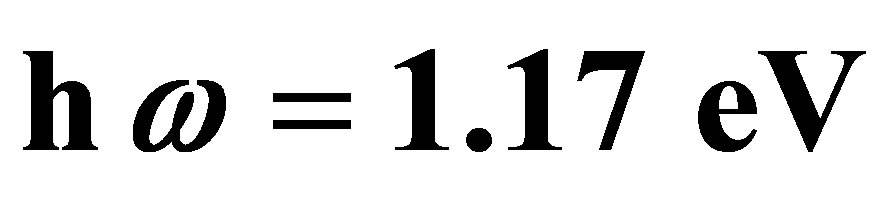 and the electric field strength is
and the electric field strength is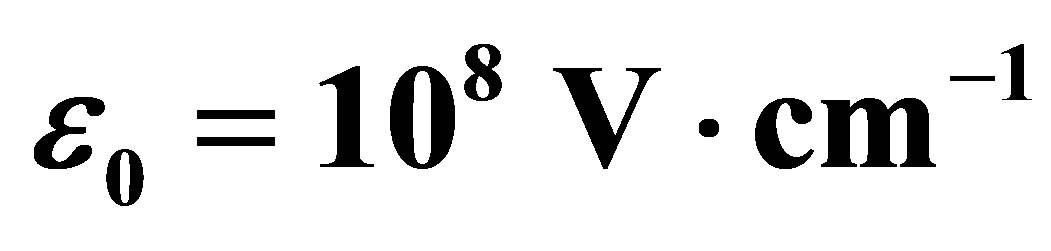 . (a) Non photon exchange (ℓ = 0) with
. (a) Non photon exchange (ℓ = 0) with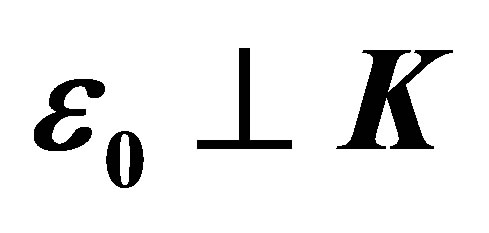 . (b) Non photon exchange (ℓ = 0) with
. (b) Non photon exchange (ℓ = 0) with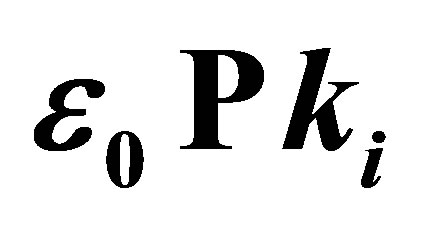 . (c) Non photon exchange (ℓ = 0) with
. (c) Non photon exchange (ℓ = 0) with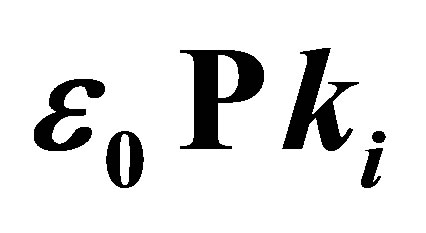 . (d) One-photon absorption (ℓ = 1) with
. (d) One-photon absorption (ℓ = 1) with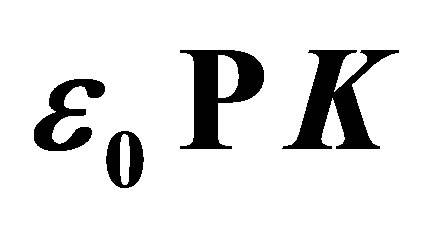 . (e) one-photon absorption (ℓ = 1) with
. (e) one-photon absorption (ℓ = 1) with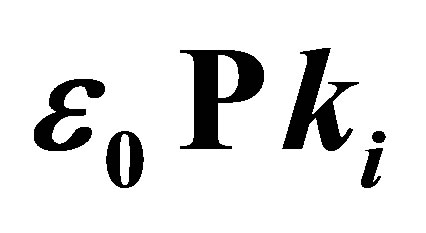 . (f) one-photon absorption (ℓ = 1) with
. (f) one-photon absorption (ℓ = 1) with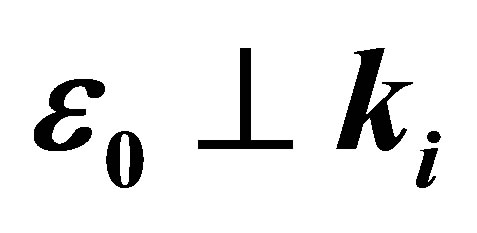 . Solid lines gives the nonperturbative results obtained by using Equatio n(23). Dashed lines give the nonperturbative results obtained by using Equation (24).
. Solid lines gives the nonperturbative results obtained by using Equatio n(23). Dashed lines give the nonperturbative results obtained by using Equation (24).
 (a)
(a)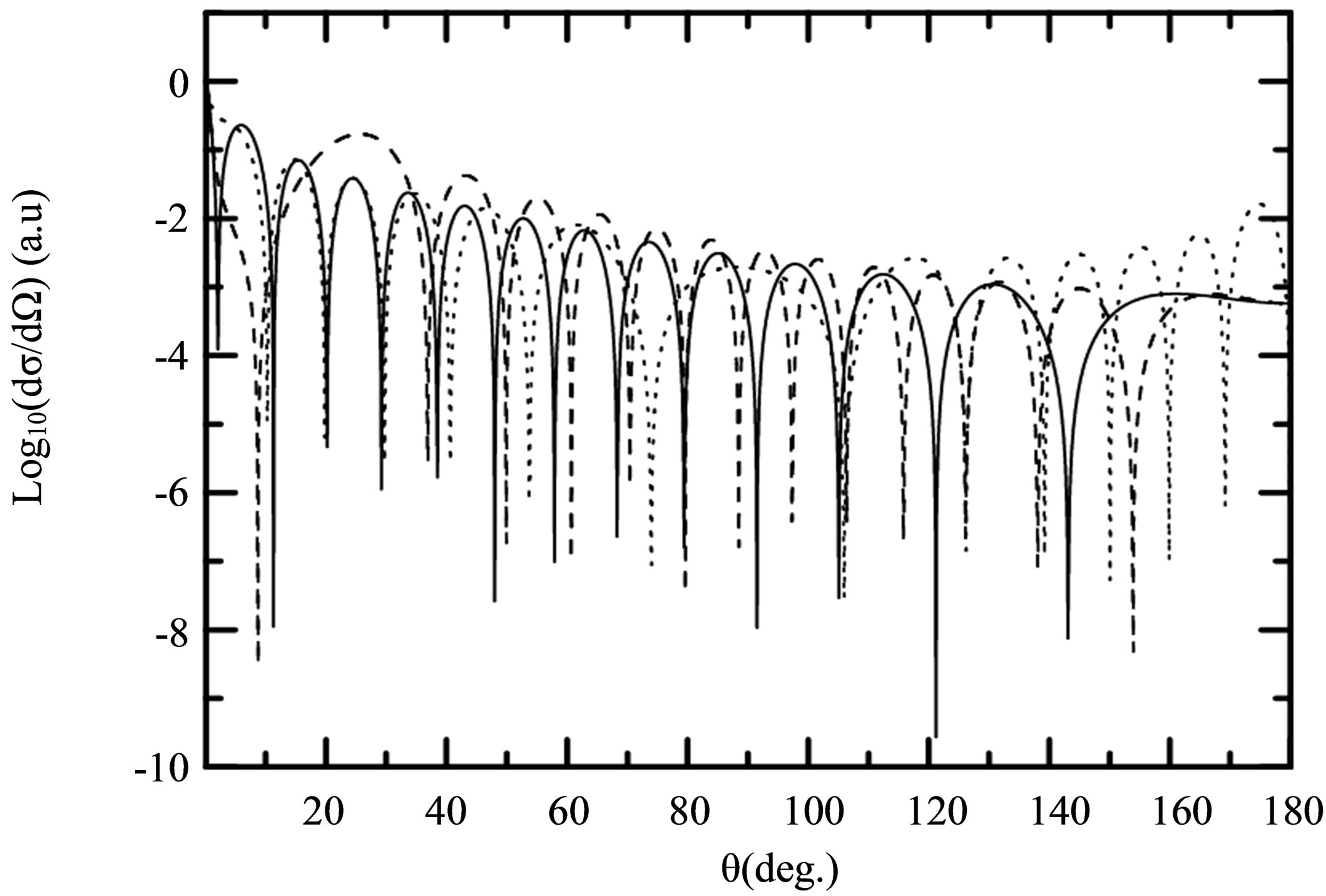 (b)
(b)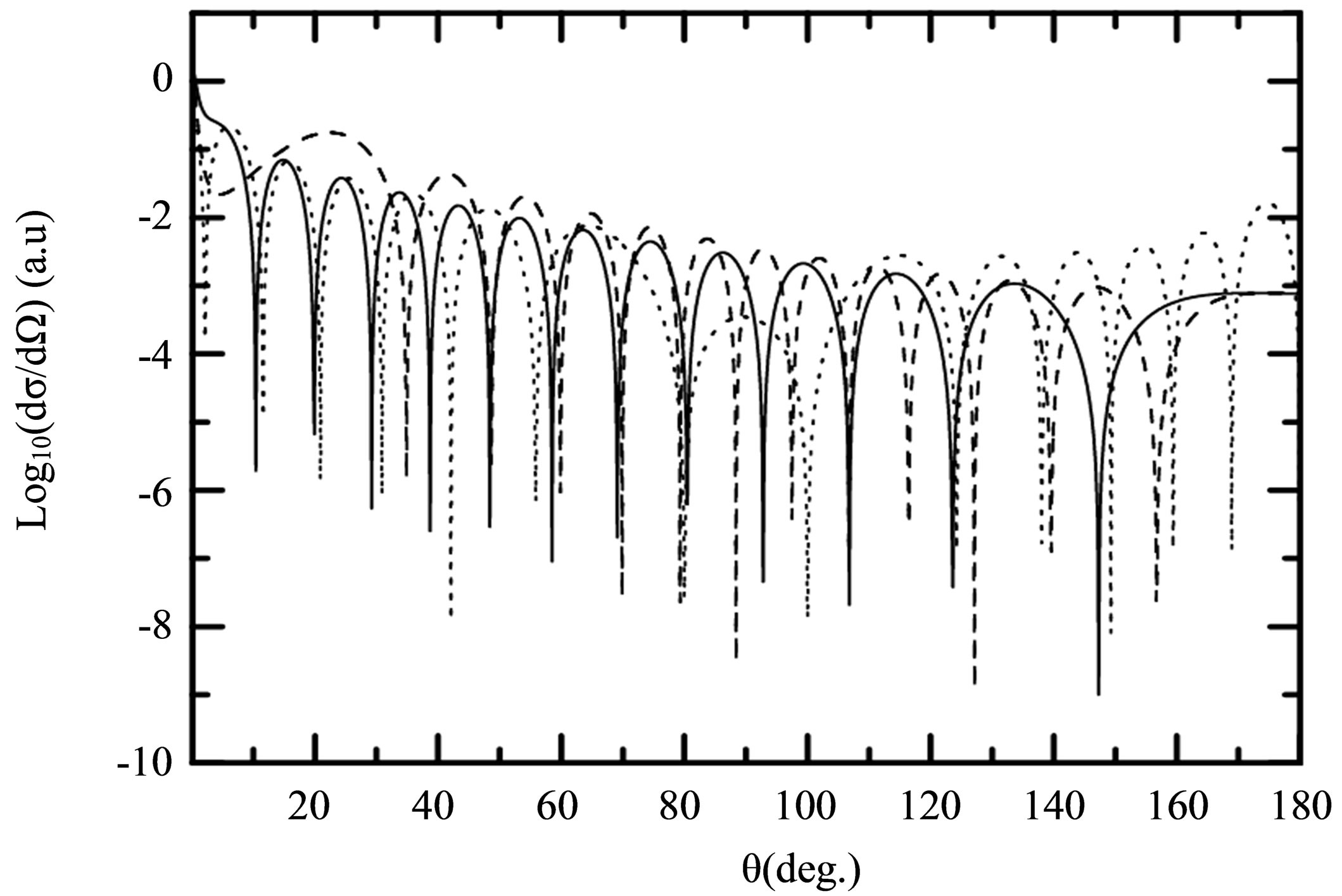 (c)
(c)
Figure 2. Variation of  corresponding to the nonperturbative results obtained by using the amplitudes of Equation (35) as function of the scattering angle θ. The incident electron energy is
corresponding to the nonperturbative results obtained by using the amplitudes of Equation (35) as function of the scattering angle θ. The incident electron energy is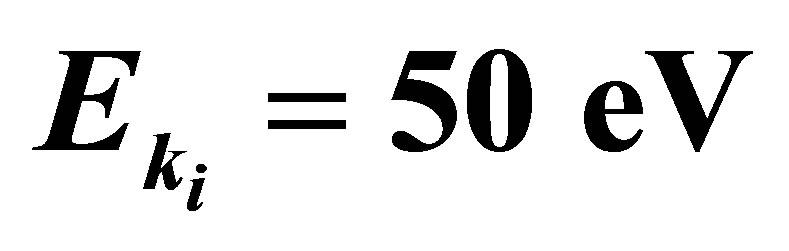 , the laser photon energy is
, the laser photon energy is  and the electric field strength is
and the electric field strength is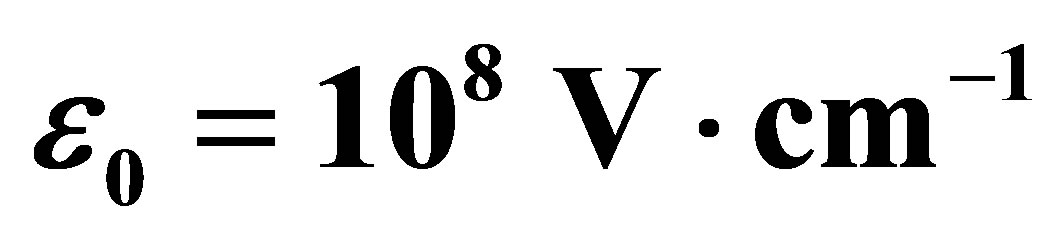 . (a) Non photon exchange (ℓ = 0), (b) One-photon absorption (ℓ = 1), (c) One-photon emission (ℓ = −1). Solid lines: The polarization vector
. (a) Non photon exchange (ℓ = 0), (b) One-photon absorption (ℓ = 1), (c) One-photon emission (ℓ = −1). Solid lines: The polarization vector 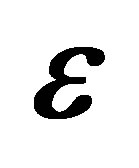 taken to be parallel to the momentum transfer direction
taken to be parallel to the momentum transfer direction . Dashed lines: The polarization vector is chosen to be parallel to the incident electron momentum direction
. Dashed lines: The polarization vector is chosen to be parallel to the incident electron momentum direction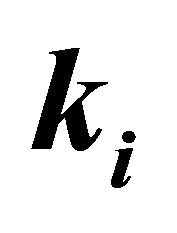 . Dotted lines: The polarization vector is chosen to be perpendicular to the incident electron momentum direction
. Dotted lines: The polarization vector is chosen to be perpendicular to the incident electron momentum direction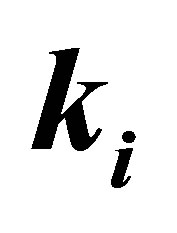 .
.
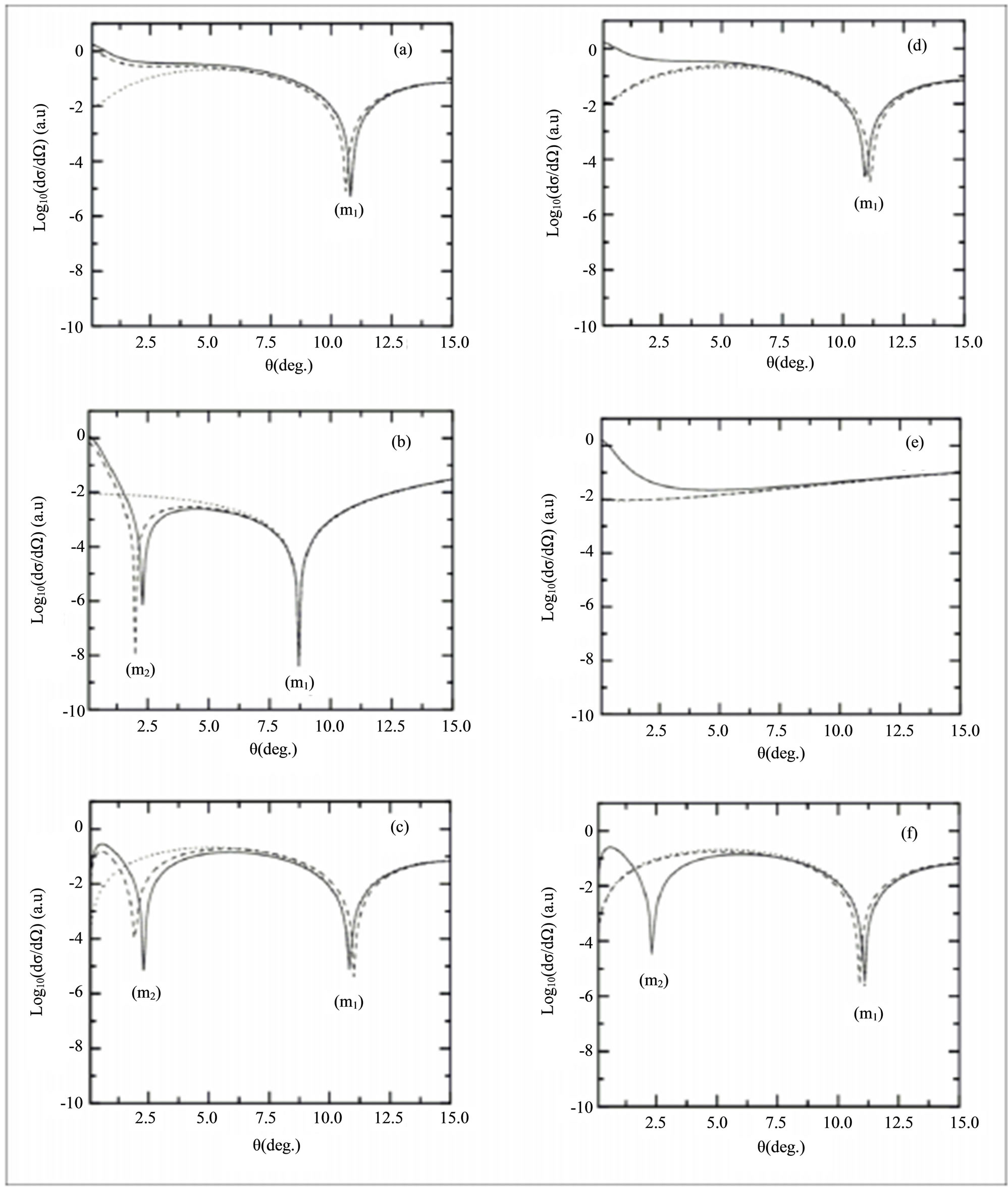
Figure 3. Variation of 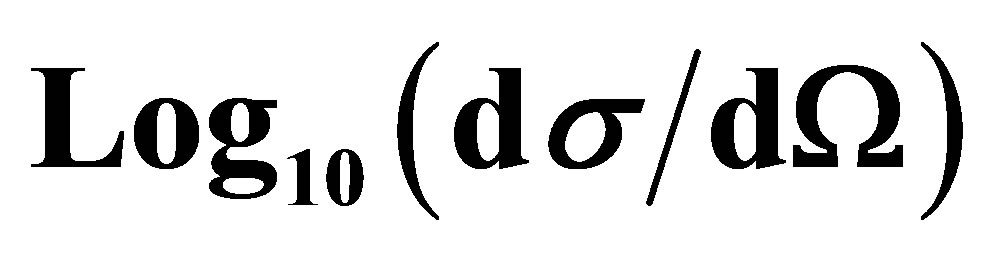 as function of the scattering angle θ. The incident electron energy is
as function of the scattering angle θ. The incident electron energy is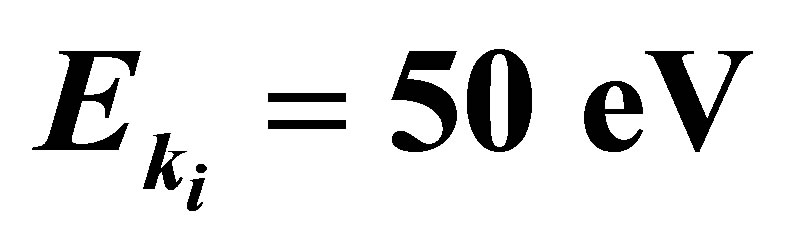 , the laser photon energy is
, the laser photon energy is  and the electric field strength is
and the electric field strength is . (a) One-photon absorption (ℓ = 1) with
. (a) One-photon absorption (ℓ = 1) with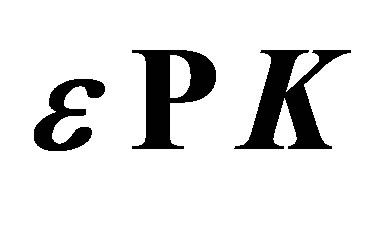 . (b) One-photon absorption (ℓ = 1) with
. (b) One-photon absorption (ℓ = 1) with . (c) One-photon absorption (ℓ = 1) with
. (c) One-photon absorption (ℓ = 1) with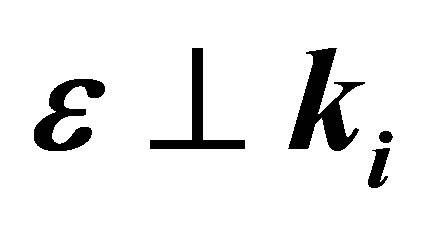 . (d) One-photon emission (ℓ = −1) with
. (d) One-photon emission (ℓ = −1) with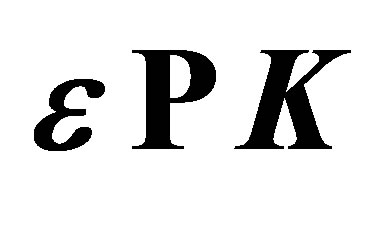 . (e) One-photon emission (ℓ = −1) with
. (e) One-photon emission (ℓ = −1) with . (f) One-photon emission (ℓ = −1) with
. (f) One-photon emission (ℓ = −1) with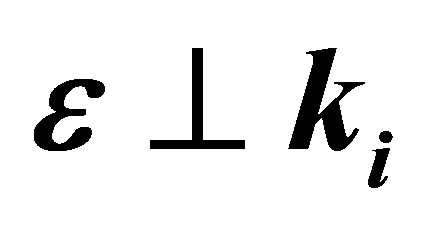 . Solid lines: The nonperturbative results obtained by using Equation (24). Dashed lines: The perturbative results. Dotted lines: The results obtained by neglecting the dressing of the target.
. Solid lines: The nonperturbative results obtained by using Equation (24). Dashed lines: The perturbative results. Dotted lines: The results obtained by neglecting the dressing of the target.
theory and to the “electronic” cross section in which dressing effects are neglected [7].
As indicated in our previous paper on elastic scattering of helium [16] and excitation of atomic hydrogen [17], we have observed the existence of two kinds of minima noted (m1) and (m2) on the differential cross sections. Both minima correspond to values of the scattering angle for which the cross section is actually zero; nevertheless the origin of these zeros is different for each case.
The minimum denoted (m1) occur in fact at angles such that the argument  of the Bessel functions actually vanishes. Those minima appear at the same angle for several curves, i.e. this product is common to the different scattering amplitudes. Moreover, we notice that those minima exist in the localization in θ is given by the following Equation
of the Bessel functions actually vanishes. Those minima appear at the same angle for several curves, i.e. this product is common to the different scattering amplitudes. Moreover, we notice that those minima exist in the localization in θ is given by the following Equation
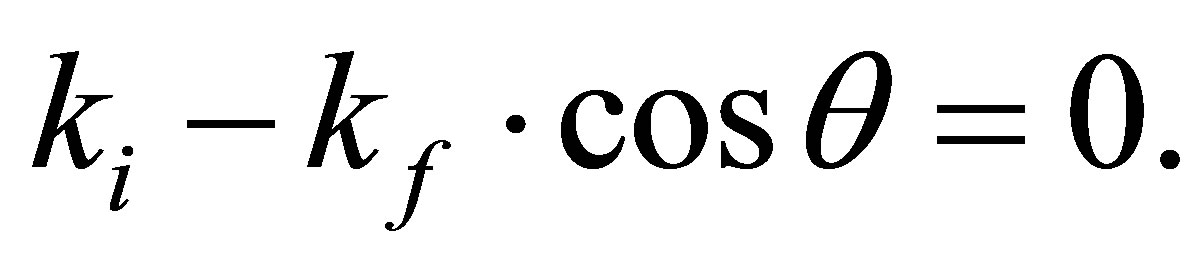 (36)
(36)
We note that the condition 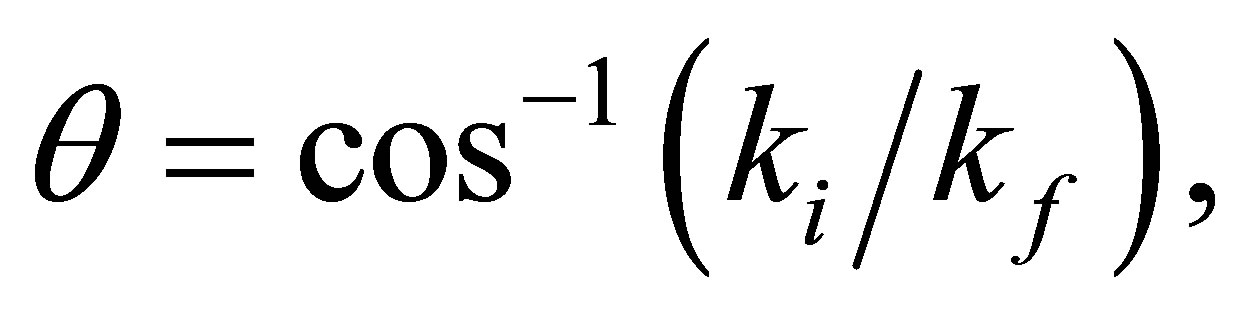 should be modified in the case of more general geometries corresponding to different orientations of laser polarization [18]. On the other hand the minimum denoted (m2) appears at angles for which the first Born differential crosssection vanishes, i.e. when
should be modified in the case of more general geometries corresponding to different orientations of laser polarization [18]. On the other hand the minimum denoted (m2) appears at angles for which the first Born differential crosssection vanishes, i.e. when  This behavior results from the fact that the resonant atomic amplitudes f2 and f3 change sign in this range and can compensate the direct contribution f1 (the direct and the atomic amplitudes are varying in opposites directions when the momentum transfer increases), which a destructive interferences. This minimum exists for absorption with net exchange of photons in the cases
This behavior results from the fact that the resonant atomic amplitudes f2 and f3 change sign in this range and can compensate the direct contribution f1 (the direct and the atomic amplitudes are varying in opposites directions when the momentum transfer increases), which a destructive interferences. This minimum exists for absorption with net exchange of photons in the cases  and
and  and only for emission in the case when
and only for emission in the case when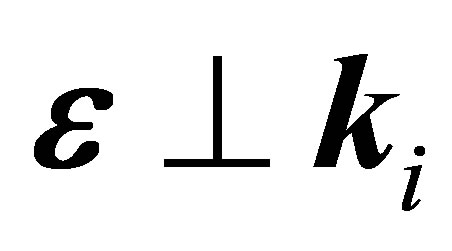 . In contrast, for the case of the laser field is chosen to be parallel to the momentum transfer
. In contrast, for the case of the laser field is chosen to be parallel to the momentum transfer  (see set of the Figure 3), the differential cross-sections display only one minimum designed (m1) because the condition
(see set of the Figure 3), the differential cross-sections display only one minimum designed (m1) because the condition 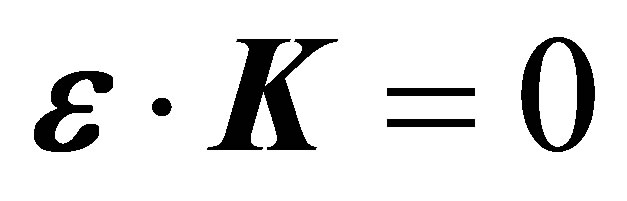 can be met at any scattering angle, while the minima (m2) disappear. For a given incident and photon energies, the absence of the minima (m1) and/or (m2) make the difference between emission and absorption, when the polarization vector of the field either parallel or perpendicular to the momentum of the incident electron
can be met at any scattering angle, while the minima (m2) disappear. For a given incident and photon energies, the absence of the minima (m1) and/or (m2) make the difference between emission and absorption, when the polarization vector of the field either parallel or perpendicular to the momentum of the incident electron . This difference comes from the condition
. This difference comes from the condition 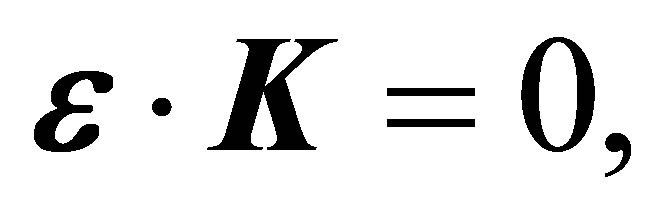 which cannot be fulfilled in the emission cases
which cannot be fulfilled in the emission cases 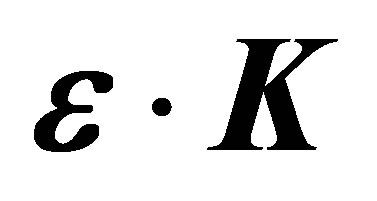 and
and 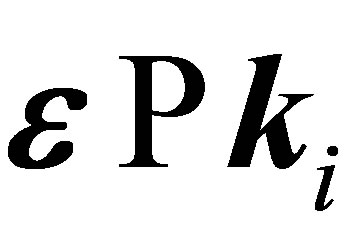 for purely kinematical reasons
for purely kinematical reasons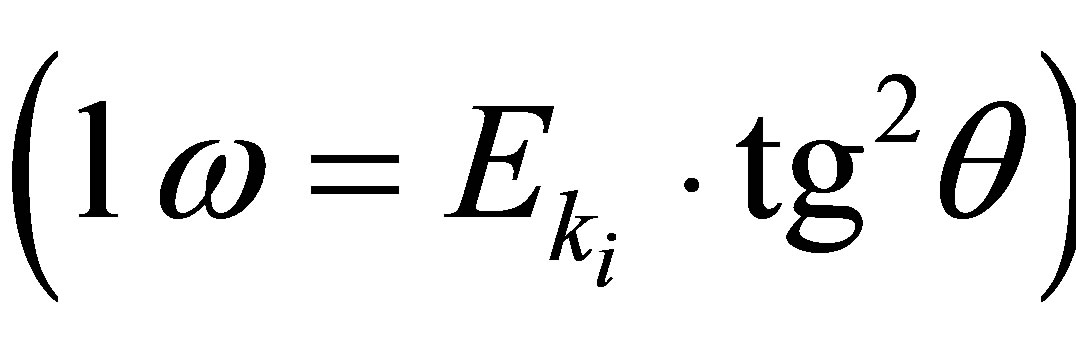 . The last condition was justified when
. The last condition was justified when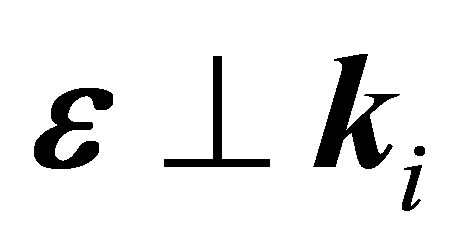 . The presence of a destructive interference between the direct f1 and the atomic amplitudes f2 and f3 is a general feature of 11S → n1S transitions, in particular for 11S → 11S, in the case of absorption ℓ ≥ 1 for
. The presence of a destructive interference between the direct f1 and the atomic amplitudes f2 and f3 is a general feature of 11S → n1S transitions, in particular for 11S → 11S, in the case of absorption ℓ ≥ 1 for 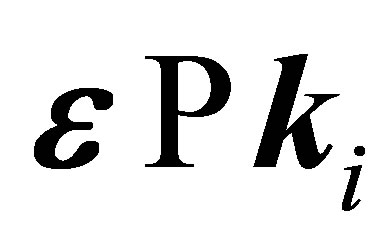 and
and 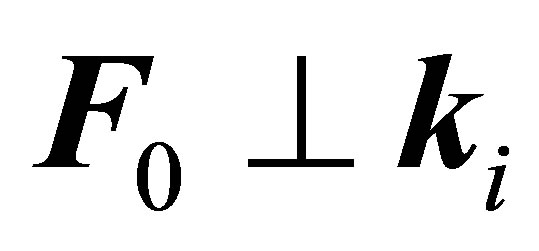 and in the case of emission ℓ ≤ 1 for
and in the case of emission ℓ ≤ 1 for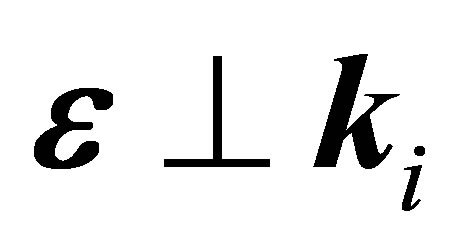 . This is due to the presence, in the atomic term (f2 + f3) of s – p transition amplitudes, which behave like K−1 for small K. This behavior can be explained by change of Bessel functions from absorption
. This is due to the presence, in the atomic term (f2 + f3) of s – p transition amplitudes, which behave like K−1 for small K. This behavior can be explained by change of Bessel functions from absorption 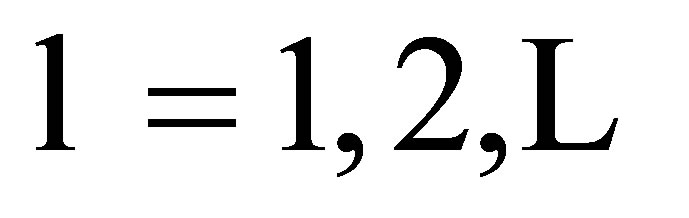 to emission
to emission  making a change of sign of the atomic amplitude (f2 + f3). This change is very important in the case when
making a change of sign of the atomic amplitude (f2 + f3). This change is very important in the case when 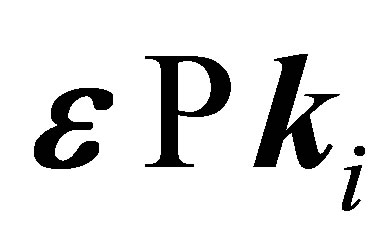 and
and .
.
In Figure 3 the shape of the differential cross section with the nonperurbative treatment follows the same behaviour that corresponds to the results obtained in the case of the first-order perturbation theory for such a choice for the field amplitude. However, the agreement between the perturbative and present treatment results corresponding to the elastic scattering, with ℓ = ±1, is occurred. Once again, except for small scattering angles with strong laser field, this agreement between both methods is excellent. Finally, this predicts important asymmetries between inverse and stimulated bremsstrahlung. That feature constitutes one of the main differences between elastic and inelastic scattering in a laser field [7].
Figure 4 shows the two-photon to one-photon freefree cross section ratio at 300 eV incident energy as a function of a laser intensity. The increase in the ratio with intensity indicates that a measurement of the ratio at 300 eV, made by deHarak et al. [5], can be used to deduce the laser intensity within the validity of the KWA and our treatment at the lowes laser intensity. The neglect of the laser-atom interaction can be carried out with moderate laser power where the KWA predicts very small, or indeed vanishing free-free cross sections under certain circumstances [5].
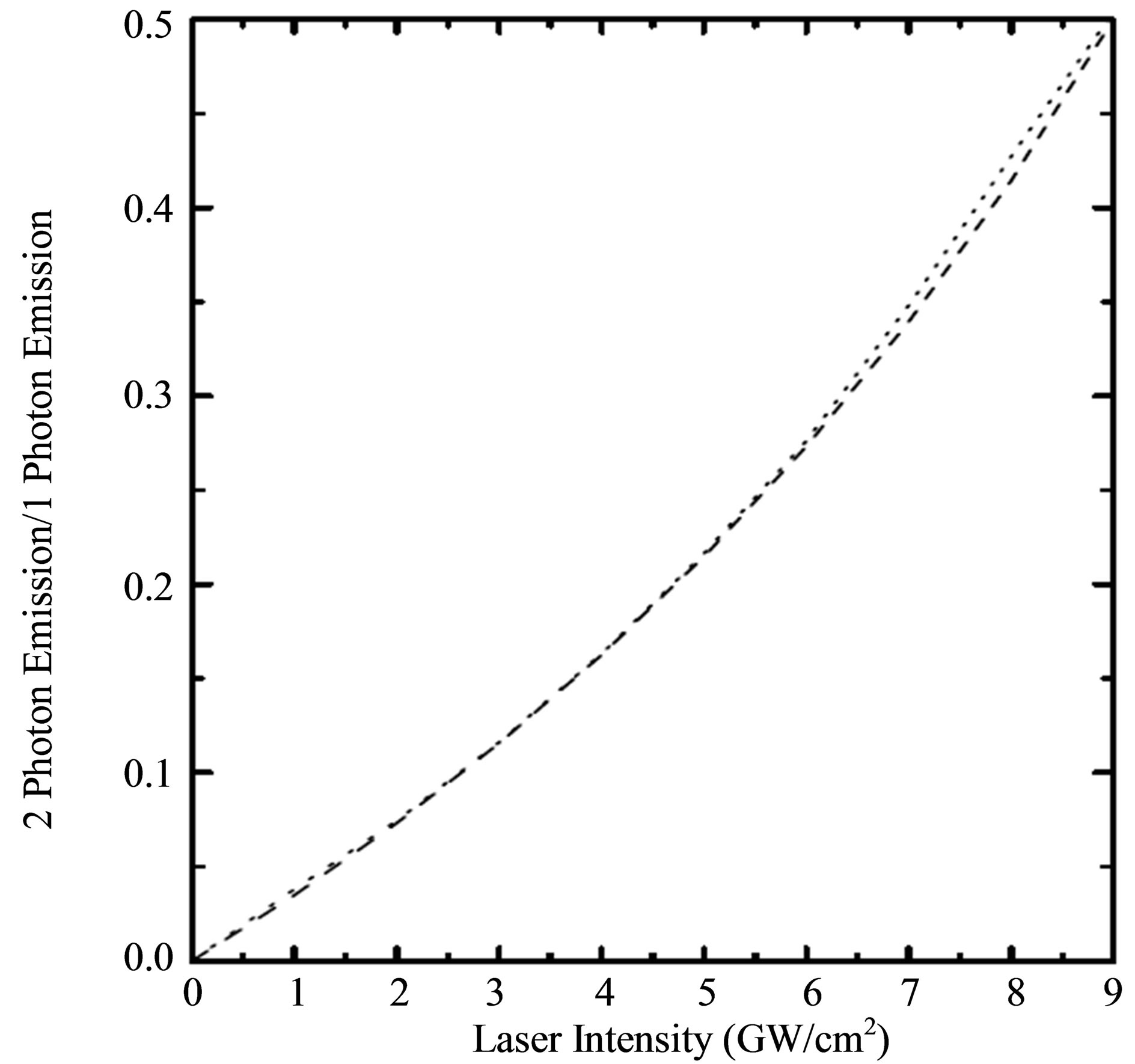
Figure 4. Variation of ratio of two-photon to one-photon emission free-free cross sections as a function of laser intensity for 300 eV incident electrons. The scattering angle is 135˚, and the laser polarization is parallel to the scattered electron direction. Dashed line: The nonperturbative results obtained by using Equation (35). Ditted line: The results obtained by deHarak et al. [5].
4. Conclusions
We have elaborated a treatment of electron-atom collisions in the presence of laser field. This treatment can be applied in the case of a nearly resonant laser field where the perturbation theory diverges. Our method treats to all the interaction of the field with the fast incident projectile, as well as the interaction of the field with the dominant (low-lying) atomic states. This latter interaction is treated by using Floquet theory of multiphoton transitions. Finally, the coupling of the laser field with the high-lying states of the atomic spectrum is treated perturbatively.
We have applied this method to the electron-helium elastic collisions, in the presence of a nonresonant laser field. The very interesting effect is that the numerical results show that during such a laser-assisted elastic collisions, the electron-atom system may exchange a great number of photons with the laser background. Each multiphoton cross sections oscillate by a few orders over the whole scattering angular region. For parallel polarization geometry , the results oscillate more frequently in the medium angular range than in the forward and backward angles; while for a perpendicular geometry
, the results oscillate more frequently in the medium angular range than in the forward and backward angles; while for a perpendicular geometry , the oscillation feature is opposite.
, the oscillation feature is opposite.
Our results have been compared with those obtained by treating the laser-atom interaction by first-order timedependent perturbation theory. The agreement between both methods is good, except close to the resonance (when the laser frequency is close to the Bohr frequency) where the perturbative cross sections diverge [7], while the nonperturbative one exhibits no maximum as a function of the laser frequency and for small scattering angle.
REFERENCES
- N. J. Mason and W. R. Newell, “Simultaneous ElectronPhoton Excitation of the Helium 23S State,” Journal of Physics B, Vol. 20, 1987, p. L323. http://dx.doi.org/10.1088/0022-3700/20/10/006
- B. Wallbank, J. K. Holmes, L. Le Blanc and A. Weingartshofer, “Simultaneous Off-Shell Excitation of He 23S by an Electron and One or More Photons,” Zeitschrift für Physik D, Vol. 10, 1988, p. 467.
- B. Wallbank, J. K. Holmes and A. Weingartshofer, “Simultaneous Electron-Photon Ex-Citation of He 23S: An Experimental Investigation of the Effects of Laser Intensity and Polarisation,” Journal of Physics B, Vol. 23, 1990, p. 2997. http://dx.doi.org/10.1088/0953-4075/23/17/012
- D. Nehari, J. Holmes, K. M. Dunseath and M. TeraoDunseath, “Experimental and Theoretical Study of FreeFree Electron-Helium Scattering in a CO2 Laser Field,” Journal of Physics B, Vol. 43, 2010, Article ID: 025203. http://dx.doi.org/10.1088/0953-4075/43/2/025203
- B. A. deHarak, L. Ladino, K. B. MacAdam and N. L. S. Martin, “High-Energy Electron-Helium Scattering in a Nd:YAG Laser Field,” Physical Review A, Vol. 83, No. 2, 2011, Article ID: 022706. http://dx.doi.org/10.1103/PhysRevA.83.022706
- F. W. Byron Jr. and C. J. Joachain, “Electron-Atom Collisions in a Strong Laser Field,” Journal of Physics B, Vol. 17, 1984, p. L295. http://dx.doi.org/10.1088/0022-3700/17/9/006
- A. Makhoute and D. Khalil, “The Effects of Laser Parameters on Electron-Atom Collisions,” Progress in Laser and Electro-Optics Research, Nova Science Publishers, Inc., 2010.
- A. Makhoute and D. Khalil, “Phase Signatures in LaserAssisted Electron-Atom Collisions,” European Physical Journal D, Vol. 46, No. 1, 2008, p. 77. http://dx.doi.org/10.1140/epjd/e2007-00280-8
- A. Makhoute, “Etude Théorique de Collisions ElectronsHelium en Présence de Champs Laser Intense,” Ph.D. Dissertation, Universite Libre de Bruxelles, Brussels, 1991.
- D. V. Volkov, “Über eine Klasse von Lösungen der Diracschen Gleichung,” Zeitschrift für Physik, Vol. 94, 1935, p. 50.
- M. Dörr, C. J. Joachain and R. M. Potvliege, “Born-Floquet Theory of Laser-Assisted Electron-Atom Collisions,” Physical Review A, Vol. 49, No. 6, 1994, p. 4852.
- G. Ferrante, C. Leone and F. Trombetta, “Laser Modifcation of the Exchange Scattering in Electron-Atom Collisions,” Journal of Physics B, Vol. 15, 1982, p. L475. http://dx.doi.org/10.1088/0022-3700/15/13/011
- J. G. Story, D. I. Duncan and T. F. Gallagher, “Landau-Zener Treatment of Intensity-Tuned Multiphoton Resonances of Potassium,” Physical Review A, Vol. 50, No. 2, 1994, p. 1607. http://dx.doi.org/10.1103/PhysRevA.50.1607
- C. J. Joachain, “Quantum Collision Theory,” North-Holland, Amsterdam, 1983.
- P. Francken, Y. Attaourti and C. J. Joachain, “LaserAssisted Inelastic Electron-Atom Collisions,” Physical Review A, Vol. 38, No. 4, 1988, p. 1785. http://dx.doi.org/10.1103/PhysRevA.38.1785
- D. Khalil, O. El Akramine, A. Makhoute, A. Maquet and R. Taïeb, “Light Polarization Eects in Laser-Assisted Elastic Electron-Helium Collisions: A Sturmian Approach,” Journal of Physics B, Vol. 31, 1998, p. 1115. http://dx.doi.org/10.1088/0953-4075/31/5/018
- M. Bouzidi, A. Makhoute and M. N. Houkonounou, “Polarisation Effect of Laser Field in Inelastic Electron-Hydrogen Collisions,” European Physical Journal D, Vol. 5, 2, 1999, p. 159. http://dx.doi.org/10.1007/s100530050239
- A. Dubois, A. Maquet and S. Jetzke, “ElectronH-Atom Collisions in the Presence of a Laser Field: One-Photon Free-Free Transitions,” Physical Review A, Vol. 34, 1986, p. 1888.
NOTES
*Corresponding author.

