Optics and Photonics Journal
Vol. 3 No. 2A (2013) , Article ID: 33339 , 6 pages DOI:10.4236/opj.2013.32A003
Infrared Transmission in Porous Silicon Multilayers
Instituto de Investigaciones en Materiales, Universidad Nacional Autónoma de México, Mexico City, Mexico
Email: *chumin@unam.mx
Copyright © 2013 Alessio Palavicini, Chumin Wang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 12, 2013; revised May 13, 2013; accepted May 22, 2013
Keywords: Porous Silicon; Multilayer; Infrared Transmission; Quasiperiodicity
ABSTRACT
Porous silicon is a nanostructured material and exhibits efficient photoand electro-luminescence in the visible range at room temperature, as well as a tunable refractive index determined by its porosity. Porous silicon samples can be obtained by etching a crystalline silicon wafer in a solution of hydrofluoric acid. In this work, we report the fabrication of porous silicon multilayers alternating layers with high and low porosities, which correspondingly produce low and high refractive indices. The free-standing multilayers were formed following three different sequences: periodic, Fibonacci and Thue-Morse. These structures were verified by scanning electron microscopy and their infrared transmission spectra were measured by means of Fourier-transform infrared spectroscopy. On the other hand, we calculate the light transmittance of porous silicon multilayers by using the transfer matrix method for all directions of incidence and a wide range of wavelengths. The experimental measurements are compared with theoretical results and a good agreement is observed. In addition, an analysis of infrared absorption peaks due to the molecular vibrations at pore surfaces reveals the presence of hydrogen and oxygen atoms.
1. Introduction
Among the large number of known semiconductors, silicon is by far the most used in electronic devices, due to its abundance on Earth’s crust and its bandgap of 1.1 eV great enough to maintain its semiconducting properties at relatively high temperatures. Moreover, silicon oxide is one of the best insulators and can be easily grown on crystalline silicon (c-Si) during the production process of metal-oxide-semiconductor field-effect transistors.
The c-Si possesses an indirect bandgap in the momentum space, which inhibits its use in light-emitting devices. In 1990, Leigh Canham found [1] an efficient photoluminescence for the visible range at room temperature in porous silicon (PSi), which can be obtained by electrochemical anodization in a hydrofluoric acid and ethanol electrolyte. The origin of this photoluminescence has been attributed to the quantum confinement and the relaxation of momentum conservation. In fact, the phonon confinement in PSi is also observed by the shift of the Raman peak towards lower frequencies [2]. Additionally, PSi has an extensive surface area of about 380 m2/g and the surface oxidation can significantly modify its optical and structural properties [3]. Another useful property of PSi is its tunable refractive index through the porosity, which is controlled by the etching conditions and mainly by the anodizing current density. This continuously varying refractive index allows the design and fabrication of multilayers by stacking PSi layers of different porosities. These multilayers can be used to make optical filters [4], waveguides [5], resonating cavities [6] and mirrors [7], where the layer ordering is crucial in the determination of their optical properties.
The layer sequence can be periodic, quasiperiodic or aperiodic, in fact, it has been observed that aperiodic multilayers could be more sensitive as resonant optical biochemical sensors than periodic ones [8]. In this article, we report a comparative study of infrared transmission in periodic, Fibonacci and Thue-Morse multilayers. Theoretical results are compared with measured transmission spectra of PSi multilayers, where infrared-activevibrational modes are also identified.
2. Transfer Matrix Method
The light transmission of dielectric multilayers can be modeled by means of the transfer matrix method [9]. Let 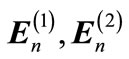 and
and 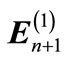 be the incident, reflected and transmitted electric fields of a plane wave whose wavevectors are
be the incident, reflected and transmitted electric fields of a plane wave whose wavevectors are 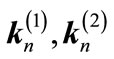 y
y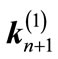 , respectively, around the interface of layers n and n + 1 as shown in Figure 1. Then, the electric field in layer n is
, respectively, around the interface of layers n and n + 1 as shown in Figure 1. Then, the electric field in layer n is
 (1)
(1)
For the case of transverse electric (TE) polarization, the propagation of light through the interface between non-magnetic layers 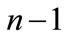 and n,
and n, 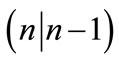 , is described by
, is described by
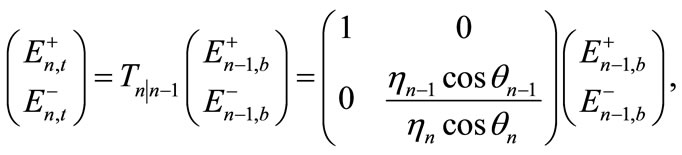 (2)
(2)
where 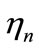 is the refractive index of layer n and
is the refractive index of layer n and
 (3)
(3)
being 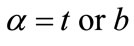 if the electric field is evaluated at the top or bottom of layer n, respectively, in accordance to Figure 1. There is also a phase change for a wave with wavelength l after propagating through a layer of thickness dn, i.e.,
if the electric field is evaluated at the top or bottom of layer n, respectively, in accordance to Figure 1. There is also a phase change for a wave with wavelength l after propagating through a layer of thickness dn, i.e., 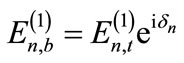 and
and  with [9]
with [9]
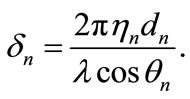 (4)
(4)
Hence,
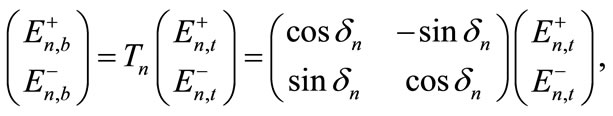 (5)
(5)
and the total transfer matrix (M) through N layers is given by
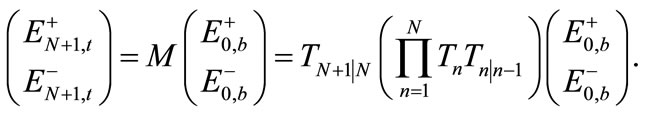 (6)
(6)
Using Equation (3), the last equation can be rewritten as
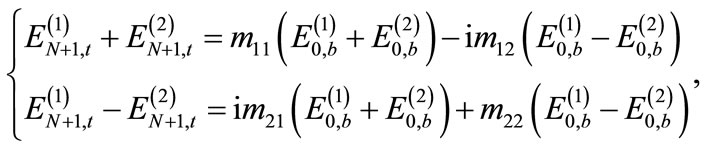 (7)
(7)
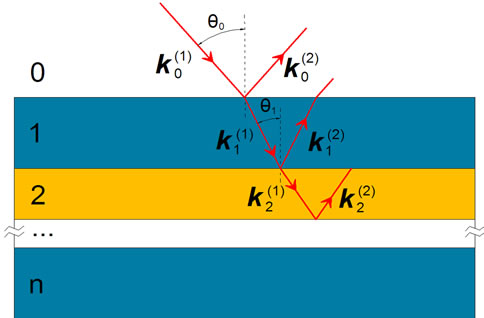
Figure 1. (Color online) Schematic representation of light propagation through a stack of N layers alternating their refractive indexes.
where  are the elements of matrix M. Notice that if the system of N layers is immersed in a single medium
are the elements of matrix M. Notice that if the system of N layers is immersed in a single medium , the determinant of matrix M is unity, because of the Snell’s law and
, the determinant of matrix M is unity, because of the Snell’s law and
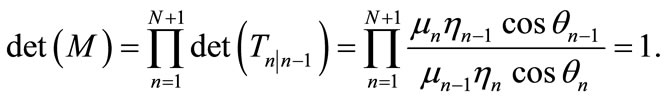 (8)
(8)
Therefore, the transmittance (T) and reflectance (R) of the multilayer are given by
 (9)
(9)
Note that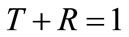 , since a multilayer made of perfect dielectricsis considered. There is an analogous deduction for the transverse magnetic (TM) polarization as done in Reference [10].
, since a multilayer made of perfect dielectricsis considered. There is an analogous deduction for the transverse magnetic (TM) polarization as done in Reference [10].
3. Multilayer Sequences
The main objective of this article is to explore the infrared transmittance of aperiodic multilayers as well as the accordance between the theory and experiment. For these purposes we have selected three multilayers with two types of layers, A and B, following periodic, Fibonacci and Thue-Morse sequences. All of these sequences can be constructed through the concatenation rules as follows. A periodic sequence of generation n  is given by
is given by 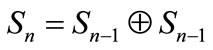 with
with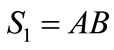 , the Fibonacci sequence by
, the Fibonacci sequence by 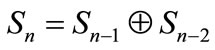 for
for 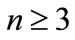 with initial conditions
with initial conditions 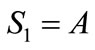 and
and , while the Thue-Morse sequence through
, while the Thue-Morse sequence through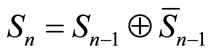 , where
, where 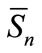 indicates the complement of
indicates the complement of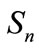 by replacing elements A by B and B by A. For example,
by replacing elements A by B and B by A. For example, 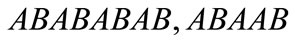 and
and 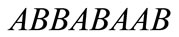 are respectively the periodic, Fibonacci and Thue-Morse sequences of generation 4.
are respectively the periodic, Fibonacci and Thue-Morse sequences of generation 4.
These sequences can also be generated by using the substitution matrices given by
given by
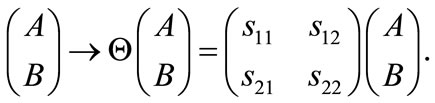 (10)
(10)
For example, the Fibonacci sequence has 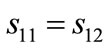
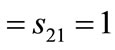 and
and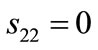 , i.e.,
, i.e., 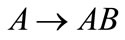 and
and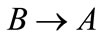 , and its matrix
, and its matrix  possesses the following eigenvalues
possesses the following eigenvalues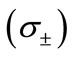 ,
,
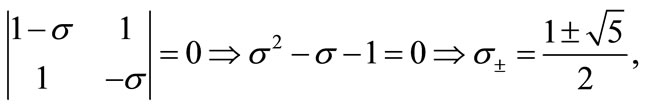 (11)
(11)
which fulfills the Pisot condition of  and
and 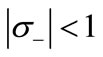 [11]. Moreover, the determinant of
[11]. Moreover, the determinant of  is unity, which along with the Pisot condition indicates that the Fibonacci sequence is quasiperiodic and produces a denselydistributed Bragg-peak diffraction spectrum [12], in contrast to the discrete Bragg peaks found in the periodic sequence.
is unity, which along with the Pisot condition indicates that the Fibonacci sequence is quasiperiodic and produces a denselydistributed Bragg-peak diffraction spectrum [12], in contrast to the discrete Bragg peaks found in the periodic sequence.
On the other hand, the Thue-Morse substitution matrix with  [11] has eigenvalues 2 and 0, which accomplish the Pisot condition. However, its determinant is not unity, so this sequence is classified into the limit-quasiperiodic case [13], which exhibits a singular continuous diffraction spectrum besides Bragg peaks [14].
[11] has eigenvalues 2 and 0, which accomplish the Pisot condition. However, its determinant is not unity, so this sequence is classified into the limit-quasiperiodic case [13], which exhibits a singular continuous diffraction spectrum besides Bragg peaks [14].
4. Fabrication of Multilayers
PSi multilayers were obtained at room temperature by electrochemical etching of p+ type c-Si wafers by alternating anodic current densities of (A) 50 mA/cm2 for 5.9 seconds and (B) 7 mA/cm2 for 21.5 seconds, as in Reference [6], leaving 1 second of null current between layers. The etching electrolyte consists of 49%wt HF and Ethanol on a 1:2 volumetric ratio. Boron-doped and [100] oriented c-Si wafers with electrical resistivity of 0.01 - 0.03 Wcm were used. The etching process was computer controlled through an Agilent 6645 A current source. In Figures 2(a)-(c) the measured time variations of applied current and voltage for periodic, Fibonacci and ThueMorse multilayers are respectively shown. At the end of the etching process an electropolishing current density of 450 mA/cm2 was applied in order to detach the multilayers from the c-Si substrate. The numbers of layers were chosen as 34 for periodic, 34 for Fibonacci and 32 for Thue-Morse, in order to have the closest number in the decades range for Fibonacci and Thue-Morse sequences.
Observe that the applied current intensities were 88.5 mA for high-porosity layers A and 12.4 mA for low porosity layers B, with an etching area of 1.77 cm2. The

Figure 2. (Color online) Current/voltage variations during the etching process of (a/a’) periodic, (b/b’) Fibonacci and (c/c’) Thue-Morse multilayers, respectively.
applied voltages had different average value for each multilayer, which was caused by the spatial location of the platinum electrode [15]. Also, along each etching process there are voltage fluctuations for a given current value in order to maintain a constant current. These fluctuations could be related to the presence of hydrogen bubbles in the electrolyte during the etching process [16]. In fact, these multilayers were fabricated using a peristaltic pump that recirculated the electrolyte at 100 mL/min, in order to remove such bubbles [15].
In Figure 3 a cross section image of Scanning Electron Microscopy (SEM) is shown for the Fibonacci multilayer, where the top dark zone corresponds to vacuum and the dark/clear grey bands are the high (A)/low (B) porosity layers. This image was obtained by using a Leica Stereoscan 400. A quantitative image analysis reveals the existence of transition zones between layers, which are not abrupt and span for about 30 nm. The width of these transition zones are too large to employ the multilayer as an electronic device but irrelevant for infrared applications.
Figures 4(a)-(c) respectively show transmittance spectra (red open circles) of periodic, Fibonacci and ThueMorse multilayers as functions of wavenumber as well as wavelength, measured by means of a Shimadzu IRAffinity-1 Fourier-transform infrared spectrometer (FTIR). These spectra are compared with theoretical results (blue solid lines) obtained by means of the transfer matrix method with refractive indexes of 1.4 for layers A and 2.1 for layers B, where the refractive index values were taken from Reference [6]. The layer thickness of layers B was taken as the average value of 150 nm from the SEM image analysis, while the thickness of layers A (225 nm) was chosen by fitting the transmittance spectrum of periodic multilayer.
Notice that there is good agreement between theoretical

Figure 3. Cross-section image of a porous-silicon Fibonacci multilayer obtained by SEM.
and experimental data, closely reproducing the diminution of oscillation period as wavenumber increasesin Figure 4(a). For Fibonacci and Thue-Morse multilayers, the theoretical results are able to predict the main features of measured transmittance spectra without any fitting parameters. Observe that besides the oscillations due to the light interference along the multilayers, there are several absorption peaks as listed in Table 1, which appear at the same wavenumber values for the three analyzed multilayers. These values are compared with absorption peaks reported in Reference [17] and their corresponding vibrational modes are illustrated in the last row of Table 1. These peaks reveal the presence of oxygen and hydrogen atoms on the surface of PSi.
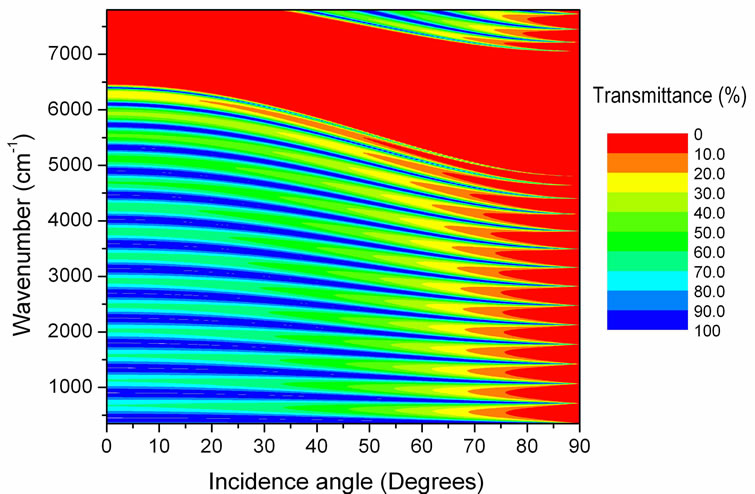
In general, the transfer matrix method allows us to calculate the light transmission spectra for all incidence angles and a wide range of wavelengths. In Figures 5(a), 5(b) and 5(c) the calculated transmittance is plotted as a function of wavelength and incidence angle for periodic, Fibonacci and Thue-Morse multilayers of 34, 34 and 32 layers, respectively, using two types of layers: A of 150 nm thickness with 1.4 refractive index and B of 225 nm thickness with 2.1 refractive index. The transmittance intensity is represented by the color scale indicated in the figures. Observe the existence of an omnidirectional reflection band with almost null transmittancefor the periodic multilayer, which is still present in the quasiperiodic Fibonacci structure. However, this band is split into three narrower sub-bands in the Thue-Morse spectrum. A Quantitative analysis by integrating the reflectance spectrum over wavenumber and incidence angle reveals that the Thue-Morse multilayer possesses the highest integrated reflectance of the three structures.
5. Conclusion
We have presented a comparative study of periodic, quasiperiodic and aperiodic multilayers by alternating high and low porosity PSi layers, which have a tunable refractive index determined by the etching current. During this etching process, voltage fluctuations to maintain a constant current were minimal due to the recirculation of electrolyte, which indicates that hydrogen bubbles were successfully removed from the surface of the wafer. The SEM analysis reveals that the thickness of the transition zone between high and low-porosity layers is about 30 nm, which is particularly suitable for infrared (IR) applications, aside from a good dielectric behavior of PSi at IR photon energies. The IR absorption peaks observed at specific wavenumbers in the three analyzed multilayers suggest their similar chemical composition at pore surface. In general, there is good agreement between measured transmittance and theoretical results, even though the latter were done for TE polarization and the spectrophotometer employs depolarized light. Also, the theory-experiment comparative results confirm the applicability of the transfer matrix method for the design of PSi multilayer structures, such as omnidirectional reflectors based on periodic and non-periodic multilayers, which are currently under study. Finally, based on the results of this study, there is no evidence to conclude that one of the three analyzed multilayers has better performance as an omnidirectional mirror than the others, despite the improved optical sensing response found in Thue-Morse
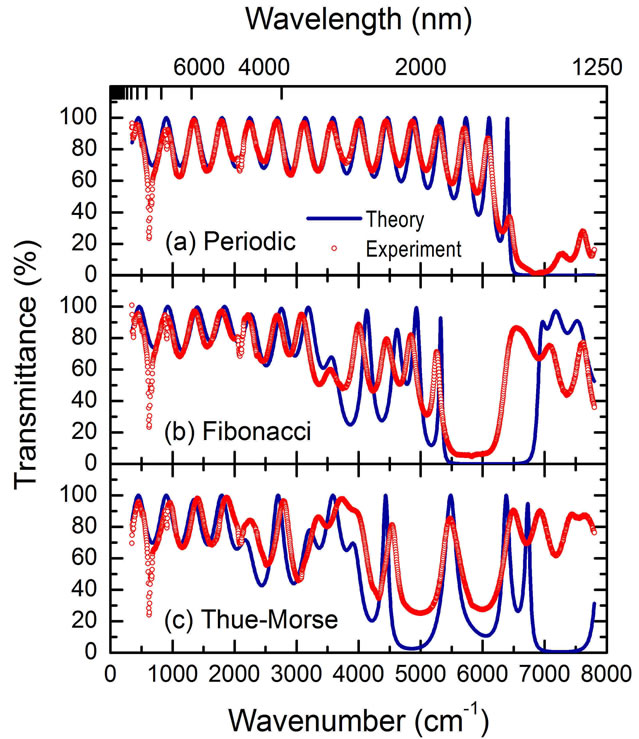
Figure 4. (Color online) Theoretical (blue lines) and experimental (red open circles) transmittance spectra as functions of wavelength and wavenumber for (a) periodic, (b) Fibonacci and (c) Thue-Morse porous-silicon multilayers.
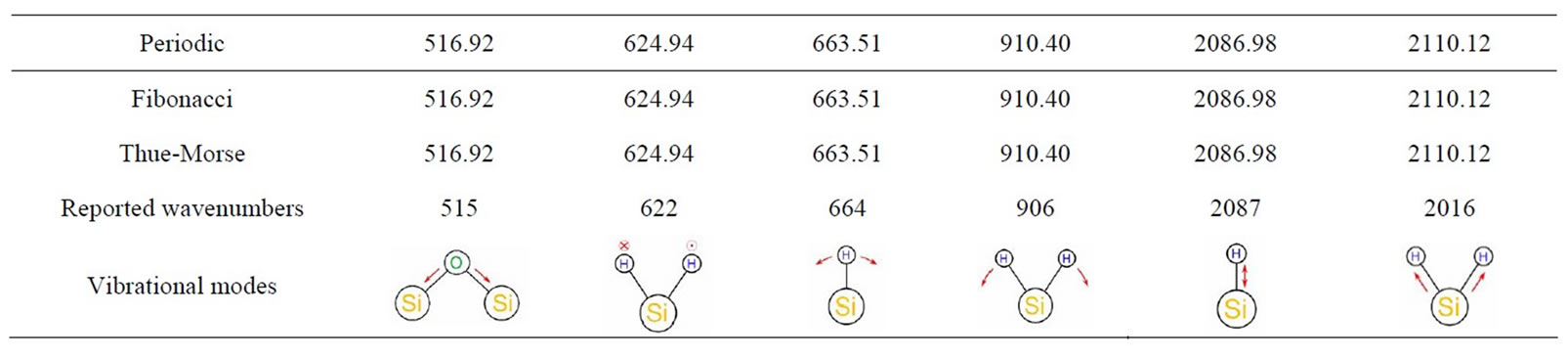
Table 1. Infrared absorption wavenumbers (cm–1) observed in Figure 4 in comparison with those of Reference [15].
 (a)
(a)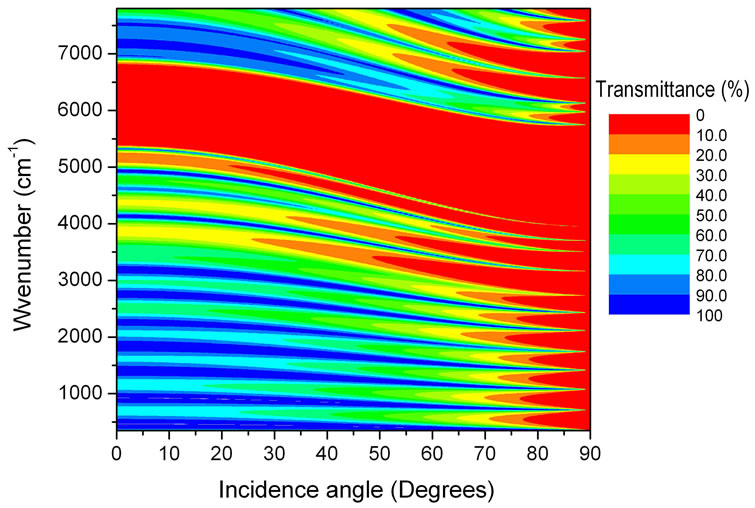 (b)
(b)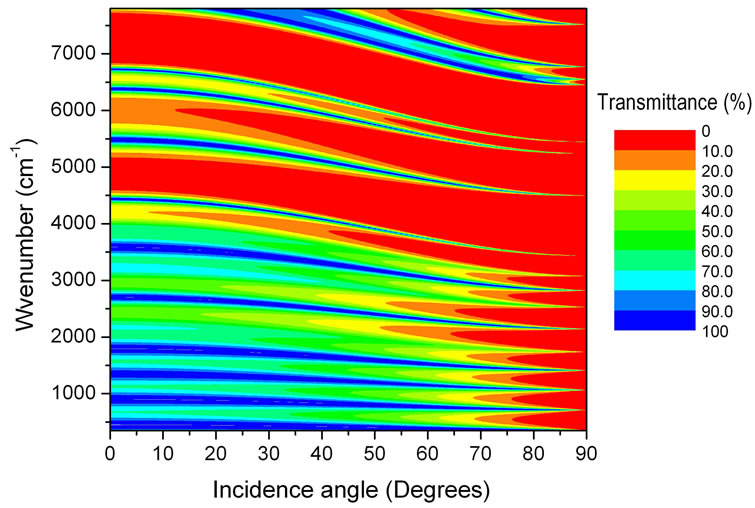 (c)
(c)
Figures 5. (a-c) (Color online) Transmittance spectra on color scale as functions of wavenumber and incidence angle for periodic, Fibonacci and Thue-Morse multilayers, respectively, alternating layers of high (type A) and low (type B) porosity. (a) Pariodic; (b) Fibonacci; (c) Thue-Morse.
[8] and Cantor [18] PSi multilayers.
6. Acknowledgements
This work has been partially supported by UNAMIN117411 and CONACyT-131596. Computations were performed at Kanbalam of DGCTIC, UNAM.
REFERENCES
- L. T. Canham, “Silicon Quantum Wire Array Fabrication by Electrochemical and Chemical Dissolution of Wafers,” Applied Physics Letters, Vol. 57, No. 10, 1990, pp. 1046- 1048. doi:10.1063/1.103561
- P. Alfaro, R. Cisneros, M. Bizarro, M. Cruz-Irisson and C. Wang, “Raman Scattering by Confined Optical Phonons in Si and Ge Nanostructures,” Nanoscale, Vol. 3, No. 3, 2011, pp. 1246-1251. doi:10.1039/c0nr00623h
- R. Cisneros, H. Pfeiffer and C. Wang, “Oxygen Absorption in Free-Standing Porous Silicon: A Structural, Optical and Kinetic Analysis,” Nanoscale Research Letters, Vol. 5, No. 4, 2010, pp. 686-691. doi:10.1007/s11671-010-9532-2
- J. Volk, J. Balázs, A.L. Tóth and I. Bársony, “Porous Silicon Multilayers for Sensing by Tuneable IR-Transmission Filtering,” Sensors and Actuators B, Vol. 100, No. 1-2, 2004, pp. 163-167. doi:10.1016/j.snb.2003.12.042
- P. Pirasteh, J. Charrier, Y. Dumeige, P. Joubert, S. Haesaert and L. Haji, “Further Results on Porous Silicon Optical Waveguides at 1.55 μm,” Physica Status Solidi A, Vol. 204, No. 5, 2007, pp. 1346-1350. doi:10.1002/pssa.200674333
- M. Ghulinyan, C. J. Oton, G. Bonetti, Z. Gaburro and L. Pavesi, “Free-Standing Porous Silicon Single and Multiple Optical Cavities,” Journal of Applied Physics, Vol. 93, No. 12, 2003, pp. 9724-9729. doi:10.1063/1.1578170
- A. Bruyant, G. Lérondel, P. J. Reece and M. Gal, “AllSilicon Omnidirectional Mirrors Based on One-Dimensional Photonic Crystals,” Applied Physics Letters, Vol. 82, No. 19, 2003, pp. 3227-3229. doi:10.1063/1.1574403
- L. Moretti, I. Rea, L. De Stefano and I. Rendina, “Periodic versus Aperiodic: Enhancing the Sensitivity of Porous Silicon Based Optical Sensors,” Applied Physics Letters, Vol. 90, No. 19, 2007, Article ID: 191112.
- M. Kohmoto, B. Sutherland and K. Iguchi, “Localization in Optics: Quasiperiodic Media,” Physical Review Letters, Vol. 58, No. 23, 1987, pp. 2436-2438. doi:10.1103/PhysRevLett.58.2436
- V. Kumar, B. Suthar, A. Kumar, V. Kumar, K. S. Singh, A. Bhargva and S. P. Ojha, “Wave Transmission in Dispersive Si-Based One Dimensional Photonic Crystal,” Optics and Photonics Journal, Vol. 2, No. 3A, 2012, pp. 237-241. doi:10.4236/opj.2012.223036
- E. Maciá, “Aperiodic Structures in Condensed Matter: Fundamentals and Applications,” CRC Press, Boca Raton, 2009, pp. 132-134.
- C. Janot, “Quasicrystals, a Primer,” 2nd Edition, Oxford University Press, New York, 1994, pp. 24-27.
- J. M. Luck, C. Godreche, A. Janner and T. Janssen, “The Nature of the Atomic Surfaces of Quasiperiodic SelfSimilar Structures,” Journal of Physics A: Mathematical and General, Vol. 26, No. 8, 1993, pp. 1951-1999. doi:10.1088/0305-4470/26/8/020
- W. Steurer, “Crytallography of Quasicrystals,” Springer, Berlin, 2009, pp. 233-234.
- R. Cisneros, C. Ramírez and C. Wang, “Ellipsometry and ab Initio Approaches to the Refractive Index of Porous Silicon,” Journal of Physics: Condensed Matter, Vol. 19, No. 39, 2007, Article ID: 395010.
- V. Lehmann, “Electrochemistry of Silicon: Instrumentation, Science, Materials and Applications,” Wiley-VCH, Berlin, 2002, p. 11. doi:10.1002/3527600272
- V. P. Tolstoy, I. V. Chernyshova and V. A. Skryshevsky, “Handbook of Infrared Spectroscopy of Ultrathin Films,” John Wiley and Sons, Hoboken, 2003, p. 452. doi:10.1002/047123432X
- J. Escorcia-García, L. M. Gaggero-Sager, A. G. Palestino-Escobedo and V. Agarwal, “Optical Properties of Cantor Nanostructures Made from Porous Silicon: A Sensing Application,” Photonics and Nanostructure—Fundamentals and Applications, Vol. 10, No. 4, 2012, pp. 452-458.
NOTES
*Corresponding author.

