Journal of Surface Engineered Materials and Advanced Technology
Vol.05 No.03(2015), Article ID:57015,11 pages
10.4236/jsemat.2015.53014
Effects of Laser Hardening Process Parameters on Case Depth of 4340 Steel Cylindrical Specimen―A Statistical Analysis
Noureddine Barka, Abderrazak El Ouafi
Mathematics, Software and Engineering Department, University of Quebec at Rimouski, Rimouski, Canada
Email: noureddine_barka@uqar.ca, abderrazak_elouafi@uqar.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2015; accepted 5 June 2015; published 10 June 2015
ABSTRACT
Laser heat treatment is considered to be one of best-performing manufacturing processes used currently due to its flexibility and its ability to develop parts with complex geometries. In fact, this process is able to produce reliable parts with hard, thin martensite and compressive residual stresses. This paper explores the heat treatment applied to 4340 cylindrical parts heated using a Nd: Yag 3 kW laser source. In this case, the hardness profile is correlated to process parameters such as the laser source power, the beam scanning speed and the revolution speed of the part during heating. Based on preliminary tests stipulating that each parameter is varied alone within a specific range, a systematic design of final tests is performed using Taguchi matrix. The obtained results are analyzed using ANOVA method to extract the effects, the contributions and the interaction between the factors. The results are then exploited to study the sensitivity of the case depth according the variation of the process parameters. The developed model exhibits good potential for converging towards a robust model able to predict the hardness curve and to generalize it for other dimensions of cylindrical parts.
Keywords:
Laser Heat Treatment, Cylindrical Specimen, Hardness Profile, Case Depth

1. Introduction
Laser processes are considered to be very high-performing processes currently used in industries. The flexibility and the precision of these processes justify their using in cutting, welding, cladding and heat treatment. Laser surface hardening is still in its early stages, with only a few years of development. Specifically, heat treatment by laser uses the high beam power density to heat parts superficially and rapidly in order to austenitize a surface layer (Regions heated above Ac3) before transforming it to hard martensite upon cooling. The region has recorded high temperature gradients due to the high heat rate. Cooling is performed by conduction, convection and radiation modes, and consequently the heated part doesn’t need an external quenching. By analyzing heat treatment by laser, the process involves the use of high intensity laser radiation to rapidly heat the surface of steel into the austenitic region [1] . Moreover, it is not clear that the steel hardenability is the same as that measured using conventional furnace heat treatment. In fact, the temperature gradient is very high because the heating rate is also high due to the capacity of the laser to concentrate an important amount of heat within a localized spot. These conditions allow the generation of a very fine, homogenous and hard microstructure [2] [3] .
To understand the process behavior and, ultimately, predict the hardness profile, few researchers focused their efforts on modeling algorithms and strategies using theory background. These researchers refer essentially to the simulation of the Gaussian sport laser, the heat transfer and some other metallurgical equations. In fact, the developed model includes the non-linear properties of the material and the heat-flow equation solved using the finite element method (FEM) [4] [5] . The FEM enables solving the governing heat-flow equation that determines the temperature distribution for each time step during heating process. The hardness is then generally approximated by the equations of Ashby and Easterling [6] . Other researchers are concentrated their efforts on experimental aspects of the process [7] [8] . In this way, the trial and error method is frequently in use to establish some useful recipes for development. In fact, to control the case depth or the compressive residual stress levels, it remains difficult to find a general model able to predict these characteristics in different operative conditions. The study of the process has never been a laborious study based on a systematic approach to better understand all the factors involved. A better investigation of interactions between different phenomena is necessary to develop a structured approach prediction models able to exploit them. The models developed to date are highly specialized and predict the hardness profile only under specific conditions and for simple geometries [9] [10] . Therefore, the models cannot be reused to predict the hardness profile for complex geometries. For example, notably lacking is a model able to predict the hardness profile according the beam power, the scanning speed and the revolution speed of cylinder heated by laser. For cylindrical shapes used especially for testing specimens and bearing seats, it is important to understand the effect of process parameters on the hardness profile before developing recipes for industrial applications. The sensitivity study could help to give a good understanding of the effects of these parameters and how the hardness profile could change in specific ranges of parameter variation.
In addition, the sensitivity analysis could contribute to a certain understanding of the effects of the main parameters of the process and demonstrate how the hardness profile could change in specific ranges of parameters variation. In this sense, the Taguchi method was used to optimize the process parameters using a laser power of 2 kilowatts fiber applied to a titanium alloy. In this study, the laser power, scanning speed and beam position have been optimized for both performance characteristics [8] . Janez researched the influence of process parameters on residual stresses of steel plates. The results obtained demonstrate that the beam power and scanning speed greatly affect the compressive residual stress level [11] . Selvan and Subramanian investigated the effects of laser parameters on the hardness and the microstructure changes using En18 steel. The obtained microstructure in the hard zone was composed of white martensite plate (1 - 2 mm size) with un-dissolved carbides. In the heated affected zone (HAZ), the microstructure essentially consisted of radial martensite with larger carbides. The un-dissolved carbide and martensite formation was attributed to the high heating rate (5000˚C/s). This study confirmed that the laser surface hardening produces wear resistance and a highly hardened surface layer consisting of metastable martensite and carbides [12] . Some other researchers have studied the effect of laser output power, beam scanning speed, and a defocused focal position on surface hardening properties. The process was applied to S45C medium carbon steel using ND: YAG 3 kW power laser with a continuous wave. The researchers have demonstrated that the Nd: YAG laser exhibits some useful advantages compared to the CO2 laser. In fact, the Nd: YAG laser allows a small spot size, a higher energy density and a higher energy absorption rate of the part [13] . Another study explored the laser heat treatment applied to AISI 4340 steel using various frequencies and amplitudes of oscillation scanning with a fiber laser power varying from 2 kW to 3 kW. Hardness profiles were measured along the center of the oscillated region in the longitudinal direction of the laser. The homogeneity of the hardness profile was investigated as a function of the process parameters and compared to conventional single track hardening [14] . The work carried out by Santhanakrishnan consisted of establishing a numerical model capable of predicting the surface temperature. The model was applied to hypo-eutectoid steel (AISI S7) heated by a laser process. Specific tests used laser power from 1.4 kW to 1.8 kW and scanning speeds from 15 mm/s to 25 mm/s. The measured temperatures (infrared pyrometer and camera) were calibrated with the thermocouples and the results obtained showed a good agreement with an error less than 4% [15] .
The main objective of this paper is to study the effects of process parameters on the hardness profile obtained for 4340 steel cylindrical specimens heat treated by laser. The main advantage of this research is to allow developing comprehensive method to understand the laser hardening process behavior. Indeed, it makes possible to quantify precisely how each process parameter can affect the case depth. Thus, the results obtained during exploration permit to develop recipe for many parts manufacturers. This work presents a preliminary effort to control and master the hardening procedures before developing advanced strategies based on monitoring of the process. In this way, the authors propose an original sensitivity study able to exhibit the effect of each parameter and their contribution, taking into consideration the laser technology, the material, the geometry and the process parameters. To reach this goal, some preliminary tests are executed in order to extract the effect of each parameter, such as power, scanning speed and revolution speed. In the second step, a systematic test plan using the Taguchi design strategy was divided to execute the final tests. The third and final step was principally focused on the study of the effects of the various factors affecting the hardness profile, and the possible interactions between them, using statistical tools.
2. Experimentation
2.1. Experimental Setup
The experiments are performed on 4340 cylinder having f 10 mm diameter. The specimens are prepared and heat treated by laser beam as they are rotated. The laser beam is set to point at the median plan of the part. A rotating testing rig is exploited during this experience. This rig is equipped by AC motor able to provide a direct drive spindle via a toothed belt. The spindle allows it to reach 10,000 RPM. The part is mounted using mixed mounting including a self-centering chuck with three jaws and a tailstock movable along the z axis, and allows centering of the parts during rotation. Figure 1 shows the experimental setup. Before starting the laser treatment, the cylinders were machined from material bars, quenched and tempered to be sure that core hardness is at 35 HRC. After laser heat treatment, the specimens are carefully prepared, polished and etched using Nital chemical solution (95% of ethanol and 5% of nitric acid). The hardness profiles were characterized by micro-hardness measurements programmed using Clemex machine.
Figure 1. Experimental setup―robotic laser cell.
2.2. Preliminary Tests
The preliminary tests have permitted the understanding of how the case depth and hardness changes with various parameters and allowed the quantification of the effects of each factor in order to converge on the choice of the final variation range. During this stage, the power, the scanning speed and the revolution speed are varied in specific ranges and the hardness curves are established using a micro-hardness machine. When one parameter is varied the two others are fixed. The power is varied from 1250 W to 1750 W by 100 W steps, the scanning speed is varied from 3 mm/s to 8 mm/s by 1 mm/s steps, and the revolution speed is varied from 500 RPM to 8000 RPM by 1500 RPM steps. The central values are 1550 W, 5 mm/s and 4000 RPM. The specimens were machined, quenched and tempered in an open furnace to reach relatively medium core hardness of about 35 HRC, indicating that the microstructure is in a relatively unstable martensitic state. The preliminary tests are useful in order to develop a rough forecasting of the process parameter effects on the hardness profile and to identify the overall range of variation. Figure 2 illustrates a metallographic image representing the hardness profile obtained with 1550 W, 5 mm/s and 4000 RPM. The hardened region seems to contain hard martensite and no melted region appears. The heat is then localized in the surface layer and the case depth is uniform according the circumference of the part. This observation is very interesting because the laser process seems very advantageous for the component development.
The hardness curve is obtained using micro-hardness measurement. In fact, the measurement is performed using Vickers hardness intendant from the surface to a specific depth. It is important to note that the hardness curves can be divided to three regions. The first region is characterized by high hardness compared to the part core. This region is completely austenitized (above Ac3) and transformed to martensite upon rapid cooling. The second region records drastic descent in hardness to reach the core hardness. This region represents the hardness loss caused by sharp drop in hardness to reach initial hardness and it is composed of a mixture of hard and over-tempered martensite since the temperature is between Ac1 and Ac3. In fact, it is heated enough, but without reaching Ac1. Consequently, this region is completely tempered by the heat flow effect. Finally, the third region corresponds to the zone not affected by the thermal flow. According to these results, the case depth (Cdep) is characterized by the first zone, called the hard zone. Figures 3-5 represent the hardness curves for the ramping tests corresponding to power (P), scanning speed (SS) and revolution speed (RS) respectively. The results demonstrate that the hardness is not maximal at the surface and stay constant within the case depth before dropping off to reach the initial hardness value, called core hardness. By analyzing the curves with respect to power, the case depth increases versus the power. The case depths are 0.6 mm, 0.8 mm and 1.2 mm for the powers 1350 W, 1550 W and 1750 W, respectively. It is also important to note that the surface hardness is maximal for high power and minimal for intermediate power. Concerning the scanning speed effect, it seems that surface hardness is similar in the three cases. The case depths are 0.2 mm, 0.55 mm and 1.2 mm for the scanning speeds 8 mm/s, 6 mm/s and 4 mm/s, respectively. One can note that when the speed is decreased from 8 mm/s to 4 mm/s (2 times less), the case depth is multiplied by factor 8. Regarding the revolution speed, the superficial hardness
Figure 2. Hardness profile―1550 W, 5 mm/s and 4000 RPM.
Figure 3. Hardness curves versus powers―5 mm/s and 4000 RPM.
Figure 4. Hardness curves versus powers―5 mm/s and 4000 RPM.
Figure 5. Hardness curves versus revolution speeds―1550 W and 5 mm/s.
seems to decrease with increasing the revolution speed. The case depths are very similar and this observation, confirming that this parameter has less influence than the power and the scanning speed.
Figure 6 illustrates the case depth as a function of increasing laser beam power. The case depth responds to the increase according to a linear relationship. It is interesting to remark that 1250 W generates a 0.4 mm case depth. An increase of 400 W generates an increased case depth of 0.6 mm. Consequently, the case depth changes from 0.4 mm to 1.0 mm. An increase of almost a quarter of the initial power doubles the value of the case depth. A third degree polynomial allows to represent the case depth depending on the power with a coefficient of determination (R2) near to 1. A strong correlation is possible between power and the case depth. The preliminary tests reveal that the case depth decreases drastically versus the scanning speed. One can remark that when the scanning speed is tuned at 3 mm/s, the case depth is about 2.8 mm; if this speed is multiplied by a factor of 3, the case depth becomes 10 times less. The effect of speed can be approximated using a polynomial function as showed in Figure 7. The case depth also increases versus the revolution speed. The evolution is quasi-linear until 6500 RPM and then increases rapidly (Figure 8). Concerning the evolution of the case depth according the scanning speed and the rotation speed, the third degree polynomials are sufficient to predict this variation. In the both case, the coefficient of determination (R2) is more than 0.99. This first analysis allow to understand the importance of the scanning speed and the laser source power and how these process parameters can affect the case depth.
Figure 6. Case depth versus power.
Figure 7. Case depth versus scanning speed.
Figure 8. Case depth versus revolution speed.
3. Experimental Design
The challenge of modeling experimental tests is closely linked to the choice of the relevant tests able to re- present adequately the variation of hardness profiles as a function of machine parameters. Due to its simplicity and transparency, systematic design based on the factorial design is usually the most commonly used model in experimentation. However, it requires an important number of tests depending on a number of factors and their levels. In this way, the Taguchi strategy conducts efficient and robust fractional designs to acquire statistically significant data with a minimal number of tests [16] . To choose the variation range for the different characteristics (case depth, surface hardness, etc.), it is important to perform some additional tests included in the Taguchi matrix based on a good knowledge of the behavior of the process. In the case of heat treatment, it is important to avoid the non-transformation to martensite and melting of the layer. The experimental tests are started by defining the low and combination levels of the three factors used (power, scanning speed and revolution speed) that are able to ensure the achievement of these conditions. The choice of three levels for initial hardness is justified by the fact that the hardness profile is affected by this hardness. Table 1 shows the factors and levels used in planning the experiments. As a result, 3 factors with 3 levels are considered. They are continuous and related to the power (P), the scanning speed (SS) and revolution speed (RS). The source power provided in W, the scanning speed in mm/s and the revolution speed in RPM are considered machine parameters. The variation range of these parameters has nominal values used to reach the nominal hardness case depth (1500 W, 6 mm/s and 4000 RPM). The design that meets this problem is a L9 matrix corresponding to 9 tests. Each test consists of performing a linear and horizontal translation of the laser beam over a distance of 30 mm while the specimen is rotating. The hardness profile is determined by examining the cross section of the specimen and measured by a micro-hardness machine as a function of the depth from the surface. The case depth (Cdep) is determined by the depth characterizing the hardened zone.
The results obtained from the L9 Taguchi matrix were exploited using the contributions and the average effects of each factor on the mean case depth. The percent contribution of any one factor reflects the portion of the total variation observed in the experiment attributed to that factor, and eventually from the interactions between the factors. The difference from 100% represents the contribution of some other uncontrolled factors and experimental errors. The effects represent another interesting way to study the effect nature of the whole parameters. As the experiments were designed using an OA, the estimates of the average effects will not be biased [16] .
4. Statistical Analysis
4.1. Results
Since the sensitivity study is conducted to explore the effects of laser process parameters on the hardness profile, the obtained results from the L9 Taguchi matrix allow the extraction of some useful data. The experimental data are summarized in Table 2. The obtained results demonstrate that case depth (Cdep) is minimal during test 3
Table 1. Factors levels.
Table 2. L9 orthogonal array and experiments results for modeling.
(1300 W, 8 mm/s and 6000 RPM) and maximal in the case of test 7 (1700 W, 4 mm/s and 6000 RPM). The case depth is 0.10 mm for test 3 and 1.90 mm for test 9.
The metallographic analysis of the hardened region allows the observation of a very fine martensitic microstructure. Figure 9 and Figure 10 present the hardness profiles corresponding to tests 7 and 3. The hardened layer follows the circular shape of the part and is composed of martensitic microstructure. These results confirm that it technically possible to control the case depth during hardening by laser process depending to the service specifications of mechanical parts such as bearing seat. It is also interesting to note that the transition region between hardened layer and the part core is not very apparent. This remark can be confirmed by the hardness curves presented in Figures 3-5. In fact, the hardness drops off rapidly from the high value recorded at the surface to core initial hardness.
4.2. Effects of Process Parameters
According to the analytic methods depicted above, the RSM model corresponding to the measured case depth (Cdep) was established. ANOVA was performed with a stepwise mode, which could eliminate the insignificant terms automatically. Table 3 presents the detailed statistical analysis. The model's F-value of 66.44 implies that the model is very significant. A p-value of less than 0.02 similarly indicates that the model term is very significant. In this case, power (P), scanning speed (SS), revolution speed (RS) and the interactive term (P × RS) are all significant model terms. Also, it is clear that scanning speed has the largest effect on the response value, laser power has less effect and revolution speed has the least effect. The three interaction terms affect the case depth less but are not neglected. The coefficient of determination (R2) is mainly used to measure the relationship between experimental data and measured data.
The contributions of the factors on the characteristics were calculated using an ANOVA study. In fact, this study allows the determination of the various effects, and the ranking of each, on the case depth (Cdep). Based on the data in Table 4, the variation of the three characteristics presents the degree of influence of each parameter on the response, and it is confirmed by the analysis of their contributions that the power affects Cdep by more than 15%, and the scanning speed contribute to the overall variation by more than 60%. The revolution speed influences depth by about 6% with an error of less than 1%. Since the error is less than 1% for the three cases, the majority of the parameters are taken into account during this study. It is important to remark on the
Figure 9. Hardness profile―Test 7.
Figure 10. Hardness profile―Test 3.
Table 3. ANOVA for case depth (Cdep).
Table 4. Contributions of machine parameters (%).
presence of interactions between the three factors. The interactions contribute to about 12% of the variation of case depth.
Figure 11 shows the effect of all parameters on the case depth (Cdep). Similar conclusions can be derived by comparing the contributions. The obtained results confirm that Cdep increases with increasing beam power and revolution speed, and with decreasing scanning speed. The ANOVA method was conducted in order to assess the significance of each parameter. For each parameter studied, the variance ratio value, F, was compared to the values from standard F-tables for given statistical levels of significance. In this way, it was concluded that within the investigated processing window, the power, the scanning speed and the revolution speed are significant for the case depth at 95% confidence.
The results presented in Table 3 allow the identification of the coefficient of determination (R2). In this case, R2 is equal to 0.9950, proving a high correlation between experimental results and predicted results. The predicted R2 of 0.9800 is in reasonable agreement with the adjusted R2 of 0.6904. Adequate precision measures the signal to noise ratio. The standard deviation related to the case depth prediction model is evaluated at 0.0786796. After eliminating the non-significant terms, the empirical relationship between the case depth and the laser process can be expressed by Equation (1). Equation (1) presents the model based on linear regression and allows the evaluation of the case depth as a function of the three factors used in the sensitivity study.
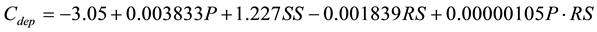 (1)
(1)
Figure 12 presents the measured and predicted curves for the case depth. The results are displayed for the 9 tests listed in Table 2. In the studied ranges of the process parameters, it is possible to predict the case depth with a good precision not exceeding 7%. The absolute difference between the measured depth and the predicted depth is less than 0.1 mm for each case. Figure 13 presents the scatter plot for Cdep. It is clear that for each measured response value, the predicted value is close to the diagonal line, due to the low value of the residuals of the predicted values. For each value of case depth, the predicted and measured curves are nearly identical, which explains the good agreement between the predicted and the measured values.
Figure 11. Effect of parameters on Cdep.
Figure 12. Measured versus predicted Cdep.
Figure 13. Scatter plot―Measured and predicted Cdep.
5. Conclusion
This paper presented a sensitivity study of hardness profiles for cylindrical specimens made of 4340 steel and heated by laser processes. The hardness profile is affected by the power, the scanning speed and the revolution speed. The preliminary tests have demonstrated that the case depth varies by different degrees according to these parameters. These tests were very insightful in defining the final ranges of variation. The final design based on Taguchi methods was chosen to represent the variation of the factors having the most influence on the hardness profile. ANOVA was exploited to study the effects and the contributions in order to identify the main parameters. The results obtained have confirmed a similarity between the case depth and the depth of the heat affected zone with respect to the contributions of the different parameters. Similarities are noted between the surface hardness and the maximal value of hardness that characterize the case depth. The scanning speed has a great influence on the depths, while the power has a greater effect on the hardness. The models are based on simple regression, allowing the prediction of hardness and depth with good precision (mean relative error less than 10%). The validation allows the characterization of good performances. The obtained results will be used advantageously to plan the modeling process and form a basis for robust prediction models.
References
- Kennedy, E., Byrne, G. and Collins, D.N. (2004) A Review of the Use of High Power Diode Lasers in Surface Hardening. Journal of Materials Processing Technology, 155-156, 1855-1860. http://dx.doi.org/10.1016/j.jmatprotec.2004.04.276
- Ricciardi, G., Cantello, M. and Micheletti, G.F. (1982) Technological Applications of the Laser Beam in Heat Treatments. CIRP Annals-Manufacturing Technology, 31, 125-130. http://dx.doi.org/10.1016/S0007-8506(07)63282-X
- Lakhkar, R.S., Shin, Y.C. and Krane, M.J.M. (2008) Predictive Modeling of Multi-Track Laser Hardening of AISI 4140 Steel. Materials Science and Engineering A, 480, 209-217. http://dx.doi.org/10.1016/j.msea.2007.07.054
- Patwa, R. and Shin, Y.C. (2007) Predictive Modeling of Laser Hardening of AISI5150H Steels. International Journal of Machine Tools and Manufacture, 47, 307-320. http://dx.doi.org/10.1016/j.ijmachtools.2006.03.016
- Mioković, T., Schulze, V., Vöhringer, O. and Löhe, D. (2006) Prediction of Phase Transformations during Laser Surface Hardening of AISI 4140 including the Effects of Inhomogeneous Austenite Formation. Materials Science and Engineering A, 435-436, 547-555. http://dx.doi.org/10.1016/j.msea.2006.07.037
- Ashby, M.F. and Easterling, K.E. (1984) The Transformation Hardening of Steel Surfaces by Laser Beams―I. Hypo- Eutectoid Steels. Acta Metallurgica, 32, 935-948. http://dx.doi.org/10.1016/0001-6160(84)90175-5
- Tani, G., Orazi, L. and Fortunato, A. (2008) Prediction of Hypo Eutectoid Steel Softening Due to Tempering Phenomena in Laser Surface Hardening. CIRP Annals-Manufacturing Technology, 57, 209-212. http://dx.doi.org/10.1016/j.cirp.2008.03.057
- Badkar, D.S., Pandey, K.S. and Buvanashekaran, G. (2011) Parameter Optimization of Laser Transformation Hardening by Using Taguchi Method and Utility Concept. International Journal of Advanced Manufacturing Technology, 52, 1067-1077. http://dx.doi.org/10.1007/s00170-010-2787-z
- Billaud, G., Barka, N., El Ouafi, A., Chebak, A. and Brousseau, J. (2014) Prediction of Hardness Profile of 4340 Steel Plate Heat Treated by Laser Using 3D Model and Experimental Validation. ASME International Mechanical Engineering Congress and Exposition, Montreal. http://dx.doi.org/10.1115/imece2014-37678
- Komanduri, R. and Hou, Z.B. (2001) Thermal Analysis of the Laser Surface Transformation Hardening Process. International Journal of Heat and Mass Transfer, 44, 2845-2862. http://dx.doi.org/10.1016/S0017-9310(00)00316-1
- Janez, G. and Roman, S. (1998) Influence of Laser Surface Melt-Hardening Conditions on Residual Stresses in Thin Plates. Surface Coating Technology, 100-10, 455-458.
- Selvan, S.J., Subramanian, K. and Nath, A.K. (1999) Effect of Laser Surface Hardening on En18 (AISI 5135) Steel. Journal of Materials Processing Technology, 91, 29-36. http://dx.doi.org/10.1016/S0924-0136(98)00430-0
- Shin, H.J., Yoo, Y.T., Ahn, D.G. and Im, K. (2007) Laser Surface Hardening of S45C Medium Carbon Steel Using ND:YAG Laser with a Continuous Wave. Journal of Materials Processing Technology, 187, 467-470. http://dx.doi.org/10.1016/j.jmatprotec.2006.11.188
- Qiu, F. and Kujanpa, V. (2012) Surface Hardening of AISI 4340 Steel by Laser Linear Oscillation Scanning. Surface Engineering, 28, 569-575. http://dx.doi.org/10.1179/1743294412Y.0000000034
- Santhanakrishnan, S. and Kovacevic, R. (2012) Hardness Prediction in Multi-Pass Direct Diode Laser Heat Treatment by On-Line Surface Temperature Monitoring. Journal of Materials Processing Technology, 212, 2261-2271. http://dx.doi.org/10.1016/j.jmatprotec.2012.06.002
- Ross, P.J. (1988) Taguchi Techniques for Quality Engineering. McGraw-Hill, New York.















