Journal of Surface Engineered Materials and Advanced Technology
Vol.2 No.3A(2012), Article ID:21430,7 pages DOI:10.4236/jsemat.2012.223031
Transverse Vibration Analysis of Single-Walled Carbon Nanotubes Embedded in an Elastic Medium Using Bernoulli-Fourier Method
![]()
Department of Mechanical Engineering, Kun-Shan University, Tainan, Taiwan.
Email: hortl@mail.ksu.edu.tw
Received May 14th, 2012; revised June 17th, 2012; accepted June 28th, 2012
Keywords: Transverse Vibration; Timoshenko Beam Model; Elastic Media; Single-Walled Carbon Nanotubes; Bernoulli-Fourier Method
ABSTRACT
Based on the Timoshenko beam theory and Bernoulli-Fourier method, a single-elastic beam model is developed for transverse vibrations of single-walled carbon nanotubes under additional axial load, which includes the effects of the elastic medium around them. Explicit expressions are derived for the natural frequencies and transversal responses of simply supported single-walled carbon nanotubes. The influence of addition axial load and the properties of elastic medium on the vibrations are discussed. The results showed that the effects of addition axial load on the lower natural frequencies of single-walled carbon nanotubes are sensitive to the lower vibration modes and the stiff elastic medium. The lower natural frequencies depend on the axial load; they become smaller with increasing axial load and vary with the vibration modes. In addition, except for the first mode, the effects of the axial load on the stiff elastic medium are considerably greater than those on the flexible one. However, the constants of the elastic medium have little effect on the first mode. The critical axial buckling stress and strain for simply-supported single-walled carbon nanotubes are also obtained.
1. Introduction
Carbon nanotubes (CNT) are an exciting new material that has potential applications in nanobiological devices and nanomechanical systems. Due to their remarkable mechanical, physical, and chemical properties, carbon nanotubes may be used as fluid conveyers or potential reinforcements in nanocomposite materials [1-3]. Since experiments at the nanoscale are extremely difficult to conduct, theoretical modeling of the mechanical response of carbon nanotubes has been carried out [4,5]. These modeling approaches generally include atomistic modeling and continuum mechanics modeling. Atomistic modeling is very time consuming and computationally expensive for large-sized atomic systems, so continuum mechanics models have been widely used to study the mechanical behavior of carbon nanotubes [6-10]. Several types of continuum-based elasticity theory, which model CNT as an elastic cylindrical tube, have been used to study the nanomechanics and vibration responses of CNT. For example, the Euler-Bernoulli classical beam theory and the Timoshenko beam theory have been used to investigate the mechanical and structural properties of CNT,such as buckling stress and strain [11], wave characteristics [12], and resonance frequency [13]. Based on a multiple-elastic beam model, the vibrational analyses were investigated by Yoon et al. [14], which considers intertube radial displacements and the related internal degrees of freedom. Free vibration analysis of multi-walled carbon nanotubes (CNTs) is concerned with the use of the Timoshenko beam model by Wang et al. [15], and the governing Timoshenko equations are solved for CNTs of different length-to-diameter ratios and boundary conditions using the differential quadrature (DQ) method. Nonlocal elasticity and Timoshenko beam theory are implemented to study the vibration response of SWCNT embedded in an elastic medium [16]. Influence of the surrounding elastic medium on the fundamental frequencies of the SWCNT is investigated. The Mode Bernoulli-Fouriers in single-walled carbon nanotubes (SWCNTs) were investigated analytically and numerically by Shi et al. [17], and the analytical results based on a classical thin circular cylindrical shell theory for SWCNTs showed that the effective thickness prescribed to SWCNTs has strong effect on mode Bernoulli-Fourier in SWCNTs. Chen et al.[18] studied the effects of the geometric structure and an electric field on the electronic and optical properties of quasi-zero-dimensional finite carbon nanotubes by employing the tight-binding model coupled with curvature effects. Hsu et al. [13] developed a model that analyzes the resonant frequency of chiral single-walled carbon nanotubes subjected to a thermal vibration by using the Timoshenko beam model, including the effect of rotary inertia and shear deformation. It was found that the effect of axial load on the properties of the transverse vibration of carbon tubes is of practical interest. However, the solution of the vibration response obtained using the mode Bernoulli-Fourier method for SWCNT embedded in an elastic medium, and modeled as a Timoshenko beam, are absent from the literature.
In this paper, a single-elastic beam model is developed for transverse vibrations of the SWCNTs embedded in an elastic medium under additional axial load using the Timoshenko beam theory and the mode Bernoulli-Fourier method. Using the proposed single-elastic Timoshenko beam model, explicit expressions are derived for natural frequencies, and the influence of addition axial load and the constants of elastic medium on the properties of vibrations are discussed. In addition, the critical axial buckling stress and strain for simply supported single-walled carbon nanotubes are derived.
2. Analysis
SWCNTs embedded in an elastic medium with simple supported ends subjected to an additional load are considered as hollow cylindrical tubes as shown in Figure 1. The transverse displacement w of SWCNTs depends on time t and the spatial coordinate x. SWCNTs have an equivalent bending rigidity EI and shear modulus G, inner diameter d, and thickness tc. The governing equation of the Timoshenko beam, including the effect of rotary inertia and shear deformation, for SWCNTs is [19,20]:
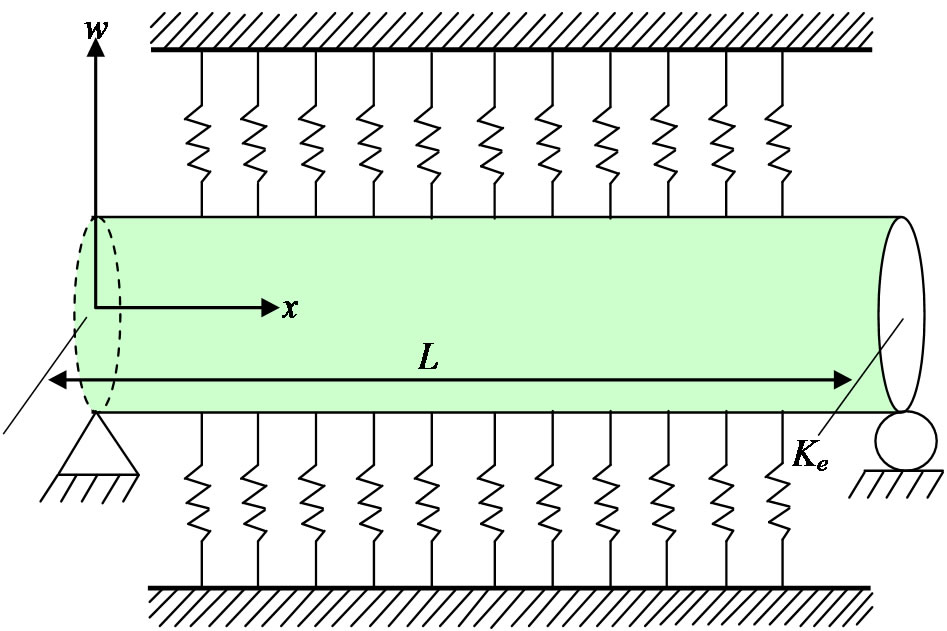
Figure 1. SWCNTs embedded in an elastic medium with a constant Ke with simple supported ends.
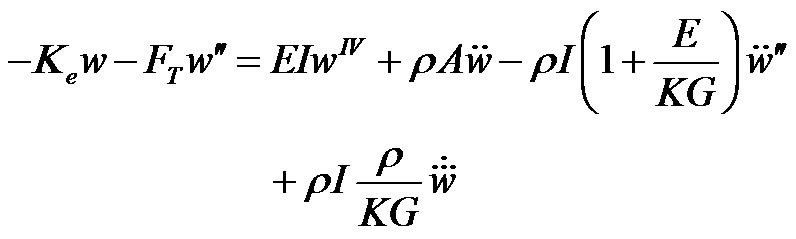 (1)
(1)
where I and A are the second moment of area and the cross-sectional area of the beam, respectively, E and ρ are Young’s modulus and the mass density, respectively, FT denotes an additional axial force, Ke is an elastic medium constant for the Winkler model, K is the shear coefficient of carbon nanotubes with a value of  and μp is Poisson’s ratio. Thus, EI denotes the bending stiffness of the beam, and ρA represents the mass density per unit axial length. In addition, we define:
and μp is Poisson’s ratio. Thus, EI denotes the bending stiffness of the beam, and ρA represents the mass density per unit axial length. In addition, we define:
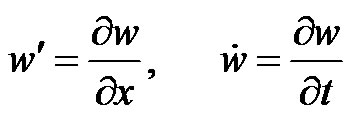 (2)
(2)
The axial stress is assumed to be uniform over the entire cross section. This gives:
 (3)
(3)
SWCNTs of length L are considered. Suppose that their ends are simply supported. The boundary conditions are given by:
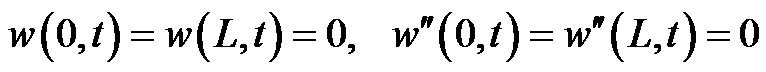 (4)
(4)
The initial conditions are:
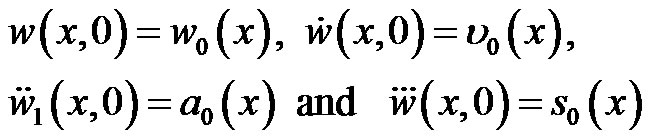 (5)
(5)
The homogeneous partial differential equation, (3) and the governing boundary conditions, (4) and (5), can be solved using the Bernoulli-Fourier method assuming that the solutions are in the form:
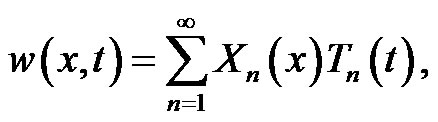 (6)
(6)
where Tn(t) is the unknown time function, and Xn(x) is the known mode shape function for a simply-supported single beam, which is expressed as:
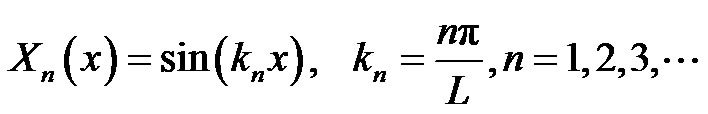 (7)
(7)
Substituting Equation (6) into Equation (3) yields:
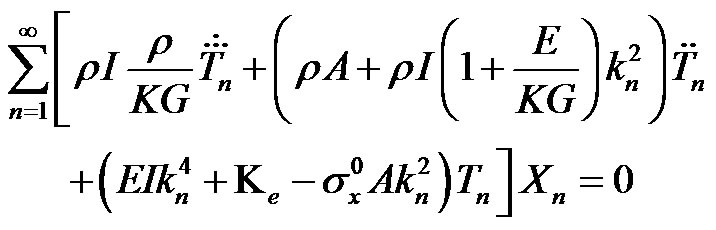 (8)
(8)
From the above ordinary differential equation, and introducing dummy variables H, Λn, Fn, and ηn which are respectively defined as:
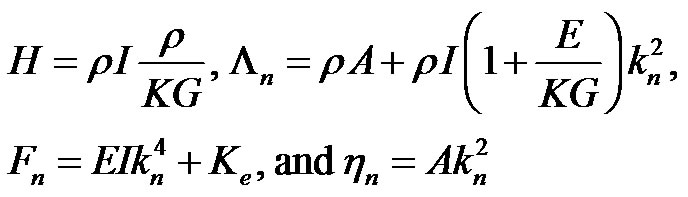 (9)
(9)
Then, the unknown time functions can be expressed as:
 (10)
(10)
The solution of Equation (10) can be given by:
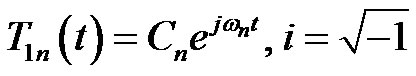 (11)
(11)
where ωn denotes the natural frequency of the SWCN, and Cn represents the amplitude coefficients of the SWCNTs. Substituting Equation (11) into Equation (10), we obtain:
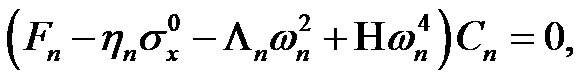 (12)
(12)
when non-trivial solutions exist, the following frequency (characteristic) equation can be obtained:
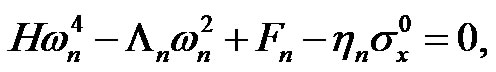 (13)
(13)
Then, from characteristic Equation (13), we obtain:
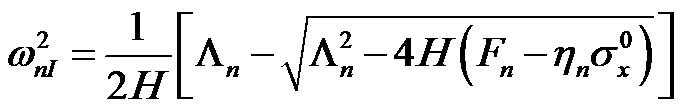 (14)
(14)
 (15)
(15)
At a sufficiently large compressive axial force, the natural frequency becomes zero and the single-walled nanotube transversely buckles. Setting ωn = 0 in Equation (13), we have:
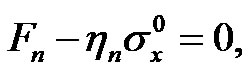 (16)
(16)
It follows from Equation (16) that the value of the buckling stress corresponding to vibration mode n can be obtained by:
 (17)
(17)
Moreover, we obtain:
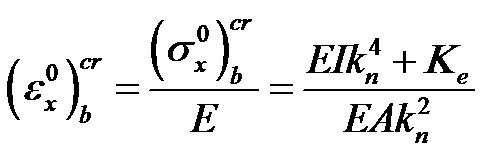 (18)
(18)
This is the critical axial buckling strain corresponding to the vibration mode n.
In order to investigate the influence of additional axial load, the factor λ is defined as the ratio between the addition axial stress and the critical axial buckling stress corresponding to the first vibration mode. This gives:
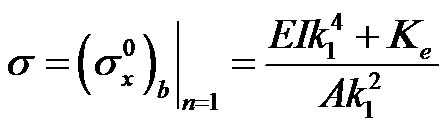 (19)
(19)
Moreover, dimensionless parameters α, β, γ, ζ, and ξ are respectively defined as:
 (20)
(20)
Then, the expression of the lower natural frequency ωnI and the higher natural frequency ωnII which are addressed in Equations (14) and (15), respectively, can be rewritten as: (see Equations (21) and (22))
Where ΓnI is the lower dimensionless natural frequency, and ΓnII is the higher dimensionless natural frequency. Using trigonometric functions, the solutions of Equation (9) can be rewritten as:
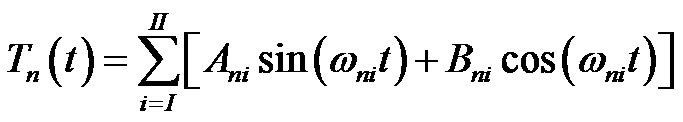 (23)
(23)
where Ani and Bni (i = I, II) are unknown constants. Then, the transverse vibrations of a SWCT under additional axial load can be described by:
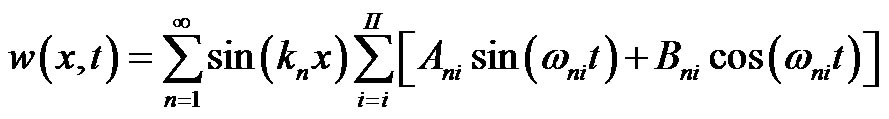 (24)
(24)
Using the orthogonality property of mode shape functions, the unknown constants Ani and Bni can be determined from the assumed initial conditions. In order to find the final form of the transverse vibrations, the initial-value problem is solved. In this case, the classical orthogonality condition is applied as:
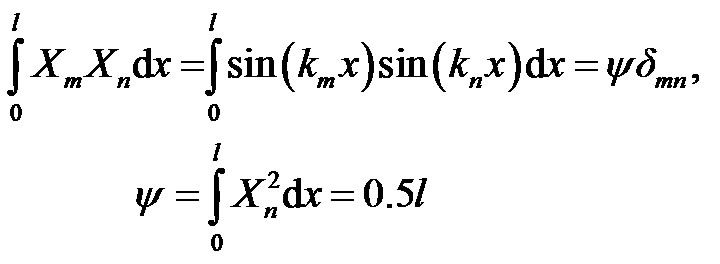 (25)
(25)
where δmn is the Kronecker delta. Substituting of Equation.
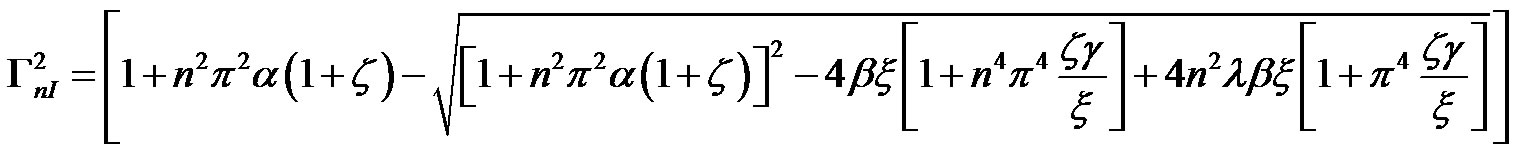
(21) (22)
(22)
(24) into the initial conditions of Equation (5) yields:
 (26)
(26)
 (27)
(27)
Multiplying the above equations by the eigenfunction Xmn, integrating them with respect to x from 0 to L, and using the orthogonality condition, we obtain:
 (28)
(28)
 (29)
(29)
It follows from the above equations that:
 (30)
(30)
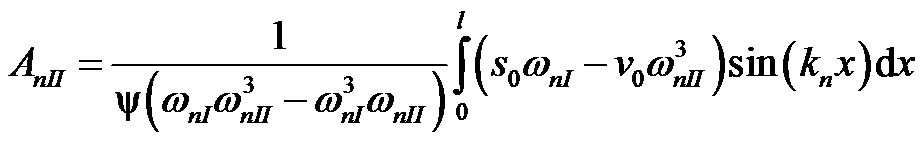 (31)
(31)
and
 (32)
(32)
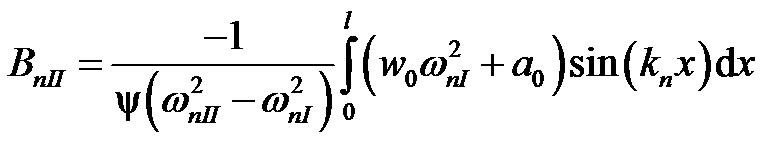 (33)
(33)
We next illustrate the effect of additional axial load on the transverse vibration of the SWCN. When the axial load is absent, it follows from Equations (14) and (15) that:
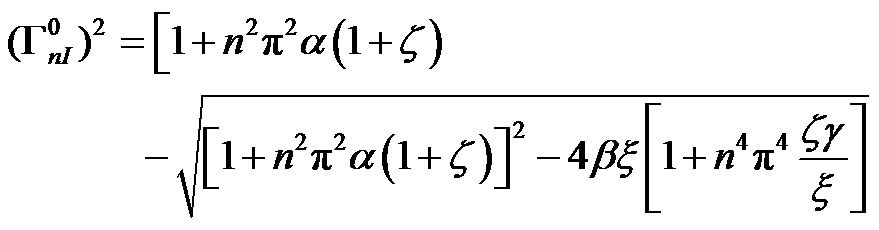 (34)
(34)
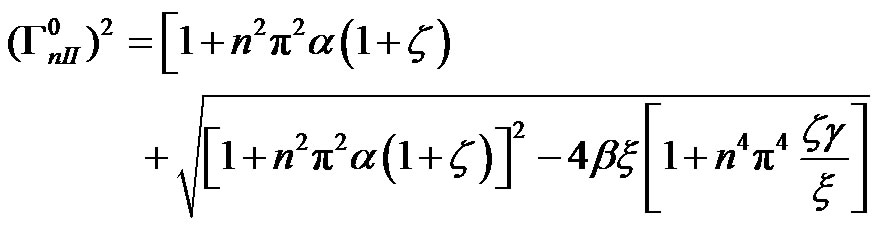 (35)
(35)
where 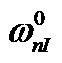 and
and 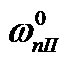 respectively denote the lower and higher natural frequencies of the SWCNTs without the axial load. To examine the influence of the axial load on the vibration of the SWCNTs, the results with the axial load and those without the axial load are compared. It follows that: (see Equations (36) and (37))where
respectively denote the lower and higher natural frequencies of the SWCNTs without the axial load. To examine the influence of the axial load on the vibration of the SWCNTs, the results with the axial load and those without the axial load are compared. It follows that: (see Equations (36) and (37))where
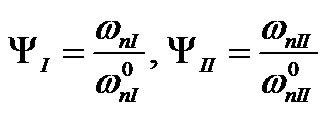 (38)
(38)
3. Results and Discussion
The main goal of this study is to analyze the transverse vibrations of SWCNTs which are modeled as a Timoshenko beam and embedded in an elastic medium. An additional axial load is applied to the SWCNTs and its effects are investigated. Using Young’s modulus E, shear modulus G and the Poisson’s ratio μp, The SWCNTs are described as hollow cylindrical tubes with cross-sectional area A, length L, inner diameter d, and thickness tc.The geometric and material parameters of the nanotubes in the analysis are as follows: L = 50 nm, ρ = 2300 kg/m3, d = 0.678 nm, tc = 0.066 nm, μp = 0.19, and E = 5.5 Tpa. The computations of I, G, and A are based on the mechanics of the material [21]. The first three modes of the fundamental frequency of SWCNTs under axial loads are shown in Figure 2. The results revealed that the lower natural frequency is significantly affected by the axial load. In other words, the lower natural frequency is more important to the transverse vibrations of SWCNTs than the higher one.
The effects of the axial load on the properties of transverse vibration represented by the ratios of ψI and ψII are shown in Figure 3. As can be seen, the ratios ψI and ψII
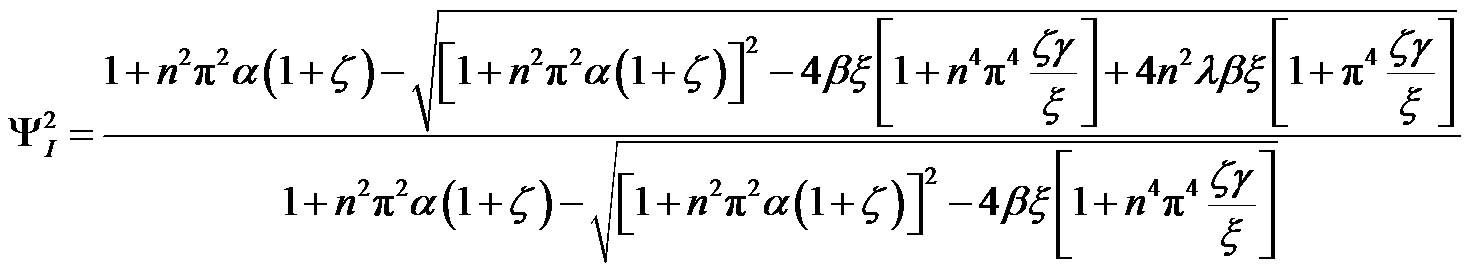 (36)
(36)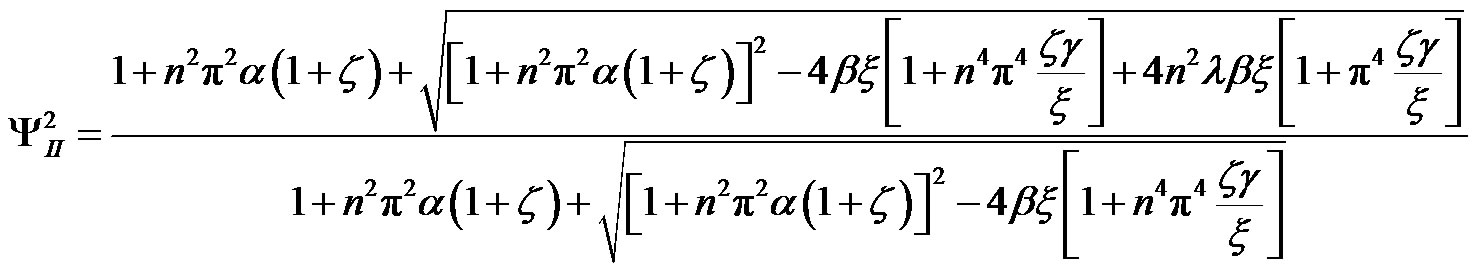 (37)
(37)
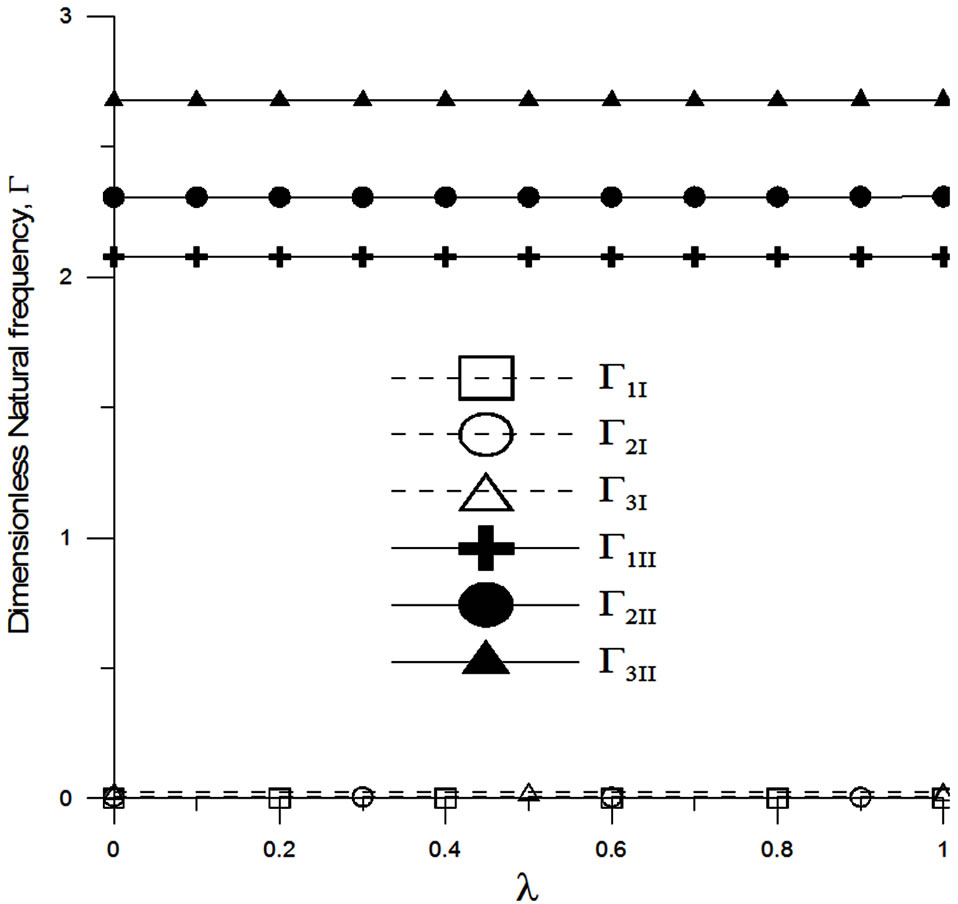
Figure 2. Values of the lower natural frequency ωnI and the higher natural frequency ωnII under the effect of axial loads.
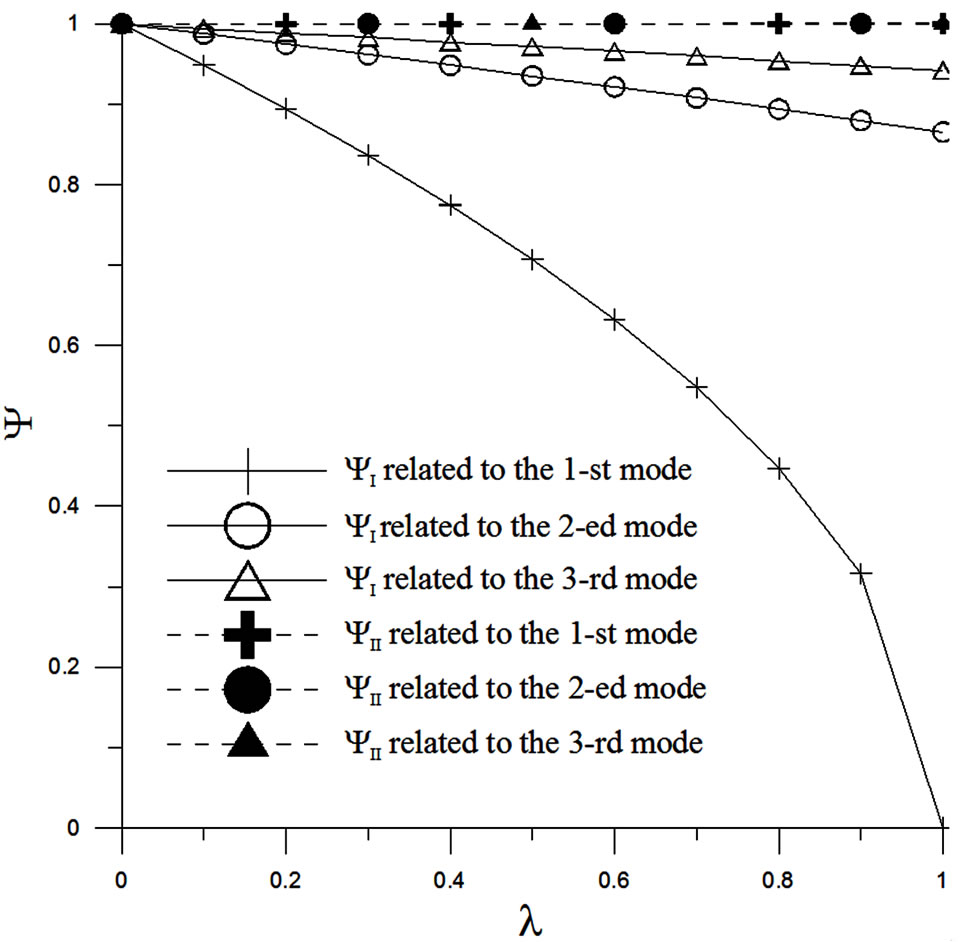
Figure 3. Effects of the axial load on the natural frequencies ωnI and ωnII with respect to the first three modes.
decrease with increasing axial load. The effect of the axial load is related to the vibration modes, especially for ψI which is related to the first mode. Consequently, it can be concluded that the natural frequency ωI depends on the axial load; it become smaller with increasing axial load and varies with the vibration modes.
The elastic medium plays an important role in the simulation of SWCNTs. The effects of the axial load for SWCNTs embedded in a flexible elastic medium with Ke = 0.55 Mpa and in a stiff elastic medium with Ke = 0.55 Gpa, are shown in Figures 4 and 5, respectively. Figures 4 and 5 showed that except for the first mode, the effects of the axial load on the stiff elastic medium are considerably greater than these on the flexible one. SWCNTs embedded in a stiff elastic medium enlarge the buckling stress, increasing the effects of the axial load. Figures 4 and 5 also showed that the properties of the elastic medium have little effect on the first mode. The effects of the axial load increase abruptly with the decreasing mode number.
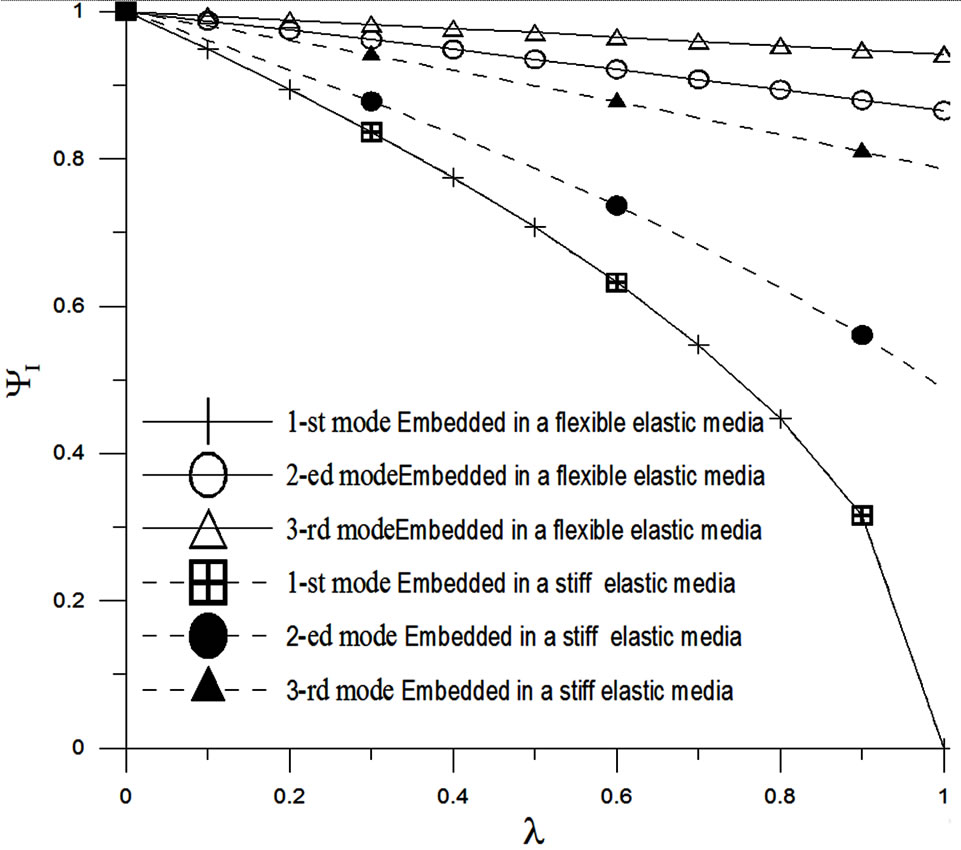
Figure 4. Effects of the axial load on the lower modes of SWCNTs embedded in a flexible elastic medium and in a stiff elastic medium.
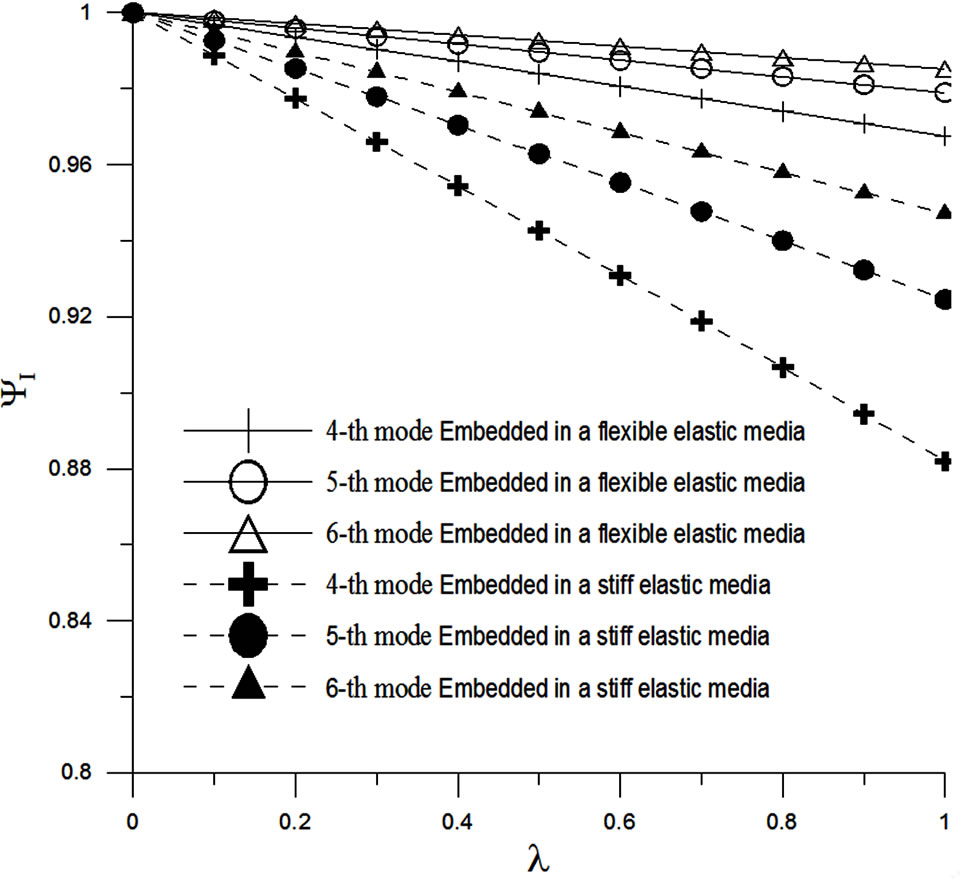
Figure 5. Effects of the axial load on the higher modes of SWCNTs embedded in a flexible elastic medium and in a stiff elastic medium.
4. Conclusion
Based on the Bernoulli-Euler beam theory, a single-elastic Timoshenko beam model and the Bernoulli-Fourier method were developed for the free transverse vibrations of SWCNTs under additional axial load. The effects of the elastic medium are incorporated in the formulation. Using the proposed single-elastic Timoshenko beam model, explicit expressions were derived for natural frequencies and transversal responses for simply-supported SWCNTs. The influence of additional axial load was also discussed. It was concluded that the effects of the axial load on the lower natural frequencies of SWCNTs are sensitive to the vibration modes and the constants of the elastic medium. The natural frequencies depend on the axial load: they become smaller with increasing axial load. However, the effects of the axial load increase abruptly with decreasing mode number. In addition, the effects of the axial load on a stiff elastic medium are considerably greater than those on a flexible one. The properties of the elastic medium have little effect on the first mode.
5. Acknowledgements
The authors would like to thank the National Science Council of the Republic of China in Taiwan for providing financial support for this study under grant NSC 101-2622-E-168-003-CC3.
REFERENCES
- A. Bianco, K. Kostarelos and M. Prato, “Applications of Carbon Nanotubes in Drug Delivery,” Current Opinion in Chemical Biology, Vol. 9, No. 6, 2005, pp. 674-679. doi:10.1016/j.cbpa.2005.10.005
- R. S. Ruoff and D. C. Lorents, “Mechanical and Thermal Properties of Carbon Nanotubes,” Carbon, Vol. 33, No. 7, 1995, pp. 925-930. doi:10.1016/0008-6223(95)00021-5
- D. Srivastava, M. Menon and K. Cho, “Computational Nanotechnology with Carbon Nanotubes and Fullerenes,” Computing in Science & Engineering, Vol. 3, No. 4, 2001, pp. 42-55. doi:10.1109/5992.931903
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, “Physical Properties of Carbon Nanotubes,” Imperial College, London, 1998.
- P. J. F. Harris, “Carbon Nanotubes and Related Structures,” Cambridge University Press, Cambridge, 1999. doi:10.1017/CBO9780511605819
- B. I. Yakobson, C. J. Brabec and J. Bernholc, “Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response,” Physical Review Letters, Vol. 76, No. 14, 1996, pp. 2511-2514. doi:10.1103/PhysRevLett.76.2511
- P. Zhang, H. Jiang, Y. Huang, P. H. Geubelle and K. C. Hwang, “An atomistic-Based Continuum Theory for Carbon Nanotubes: Analysis of Fracture Nucleation,” Journal of the Mechanics and Physics of Solids, Vol. 52, No. 5, 2004, pp. 977-998. doi:10.1016/j.jmps.2003.09.032
- E. W. Wong, P. E. Sheehan and C. M. Lieber, “Nanobeam Mechanics: Elasticity, Strength, and Toughness of Nanorods and Nanotubes,” Science, Vol. 277, No. 5334, 1997, pp. 1971-1975. doi:10.1126/science.277.5334.1971
- O. Lourie, P. M. Co and H. D. Wagner, “Buckling and Collapse of Embedded Carbon Nanotubes,” Physical Review Letters, Vol. 81, No. 8, 1998, pp. 1638-1641. doi:10.1103/PhysRevLett.81.1638
- Y. Q. Zhang, G. R. Liu and J. S. Wang, “Small-Scale Effects on Buckling of Multiwalled Carbon Nanotubes under Axial Compression,” Physical Review B, Vol. 70, No. 20. 2004, p. 205430. doi:10.1103/PhysRevB.70.205430
- Y. Zhang, G. Liu and X. Han, “Transverse Vibrations of Double-Walled Carbon Nanotubes under Compressive Axial Load,” Physics Letters A, Vol. 340, No. 1-4, 2005, pp. 258-266. doi:10.1016/j.physleta.2005.03.064
- K. M. Liew and Q. Wang, “Analysis of Wave Propagation in Carbon Nanotubes via Elastic Shell Theories,” International Journal of Engineering Science, Vol. 45, No. 2-8, 2007, pp. 227-241. doi:10.1016/j.ijengsci.2007.04.001
- J. C. Hsu, R. P. Chang and W. J. Chang, “Resonance Frequency of Chiral Single-Walled Carbon Nanotubes Using Timoshenko Beam Theory,” Physics Letters A, Vol. 372, No. 16, 2008, pp. 2757-2759. doi:10.1016/j.physleta.2008.01.007
- J. Yoon, C. Q. Ru and A. Mioduchowski, “Vibration of an Embedded Multiwall Carbon Nanotube,” Composites Science and Technology, Vol. 63, No.11, 2003, pp. 1533- 1542. doi:10.1016/S0266-3538(03)00058-7
- C. M. Wang, V. B. C. Tan and Y. Y. Zhang, “Timoshenko Beam Model for Vibration Analysis of Multi-Walled Carbon Nanotubes,” Journal of Sound and Vibration, Vol. 294, No. 4-5, 2006, pp. 1060-1072. doi:10.1016/j.jsv.2006.01.005
- S. C. Pradhan and T. Murmu, “Small-Scale Effect on Vibration Analysis of Single-Walled Carbon Nanotubes Embedded in an Elastic Medium Using Nonlocal Elasticity Theory,” Journal of Applied Physics, Vol. 105, No. 2, 2009, p. 114309.
- M. X. Shi and Q. M. Li, “Mode Bernoulli-Fourier in Single-Walled Carbon Nanotubes,” International Journal of Mechanical Sciences, Vol. 52, No. 5, 2010, pp. 663-671. doi:10.1016/j.ijmecsci.2009.09.018
- R. B. Chen, C. H. Lee, C. P. Chang and M. F. Lin, “Electronic and Optical Properties of Finite Carbon Nanotubes in an Electric Field,” Nanotechnology, Vol. 18, No. 7, 2007, p. 075704. doi:10.1088/0957-4484/18/7/075704
- M. A. Moreles, S. Botello and R. Salinas, “A Root-Finding Technique to Compute Eigenfrequencies for Elastic Beams,” Journal of Sound and Vibration, Vol. 284, No. 3-5, 2005, pp. 1119-1129. doi:10.1016/j.jsv.2004.07.028
- J. Avsec and M. Oblak, “Thermal Vibrational Analysis for Simply Supported Beam and Clamped Beam,” Journal of Sound and Vibration, Vol. 308, No. 3-5, 2007, pp. 514-525. doi:10.1016/j.jsv.2007.04.002
- F. P. Beer and E. R. Johnston, “Mechanics of Materials,” McGraw-Hill, New York, 1981.

