Geomaterials
Vol.4 No.1(2014), Article ID:42113,9 pages DOI:10.4236/gm.2014.41003
Experimental Study of Stockpiles of Iron Ore Fines
Department of Mining Engineering, Federal University of Minas Gerais, Belo Horizonte, Brazil
Email: evandrodagama@gmail.com
Copyright © 2014 Evandro Moraes da Gama et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Evandro Moraes da Gama et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 29, 2013; revised November 29, 2013; accepted December 6, 2013
Keywords:Granular Pile; Rigidity; Behavior Pellet Feed Pile; Scale Model; Discrete Element Modeling
ABSTRACT
Storage of iron ore pellet feed fines (with 90% minimum granulometry of <45 μm and 100% <150 micron) can be studied through the mechanics of granular materials. Geotechnical inputs are not able to explain the failure phenomenon comprehensively. Yet, in the industry the trend is to work with geotechnical inputs and an exaggerated degree of visual interpretation. The first part of this article briefly shows some articles in which authors emphasize the mechanics of granular materials and an article placing emphasis on the geotechnical features of granular materials. The second part shows the solution to the equation developed by [1] applied to the geometry of iron ore storage piles. The scale model study of stress variation on the model’s axis is done and the comparison of the stress variation and Thamwattana’s analytical resolution is commented. The third part shows a stress distribution study formulating centered finite differences by applying the Itasca Consulting Group’s PFC2D software to the iron ore stockpile within the same footprint as the stockpile in the analytical model. This study’s conclusions are as follows: 1) The differential between the models is the differences between tangential and normal rigidity. These differences between tangential rigidity Kt and normal rigidity Kn make the stockpile unstable. We can state that when Kn = Kt the stockpiles are more stable. 2) The models and all the work done show that the stockpiles are not stable. The stockpiles are at times temporarily stable, but even after formation, these stockpiles are unstable and the particles are always moving.
1. Introduction
Granular materials are plentiful in nature, and it is also estimated that they comprise 75% of raw materials stockpiled in industries. Knowledge of their properties, behaviors and of the forces operating in such systems is important for stocks to be handled safely, as well as for designing equipment to process and transport such materials (Figure 1).
The simplest example of a granular material system is a grain stockpile. These stockpiles may vary in volume, from a small stockpile of sand made by a person to a far greater scale in the case of industries, notably in the mining industry. These industrial stockpiles are more often conical, but can be prismatic in shape, overlapping conical and kidney-shaped (circular), depending on their construction methodology and contours.
Stockpiling of ore fines (pellet feed) as well as fine granular materials means risking loss of materials and human lives. Not infrequently we find stockpiles of fines stored at ports of shipment and stockyards suddenly fail-

Figure 1. Failure of a pellet feed stockpile at the port of Vitoria.
ing. This article is a comprehensive study on the stability of iron ore fine (pellet feed) stockpiling. The first part briefly addresses the state of the art where the authors emphasize the mechanics of granular materials and an article focusing on geotechnical granular materials. The second part shows the solution to the equation developed by [1] applied to the geometry of iron ore stockpiles. The study of stress variation using a scale model is performed. The comparison of the stress variation with the analytical solution [1] is commented. The third part shows an iron ore stockpile study highlighting stress distribution by formulating discrete elements.
2. A Brief History
Intuitively, we expect that the maximum tensile stress at the base of a stockpile occurs directly below the top of the pile; however experimental results [2] show that the point of maximum pressure is located at an intermediate position between the center and the edge of the stockpile. This motivated the development of discrete and computational models in an attempt to explain this phenomenon called “stress dip effect”.
In an attempt to formulate an analytical solution to the stockpile problem [1], it posits a theoretical stockpile made up of two regions, an outer plastic region in which the material is found in limit equilibrium and an elastic inner region in which the material is found to be in equilibrium (Figure 2). Numerical results show that, for a stockpile standing entirely on limit equilibrium, the problem’s equations can only be solved when the friction angle is 90˚, so it can be assumed that not all of the stockpile material is in limit equilibrium.
Continuum medium mechanics applied to granular environments [1] sheds light on working out a solution to the Mohr-Coulomb criterion from basic equilibrium equations:
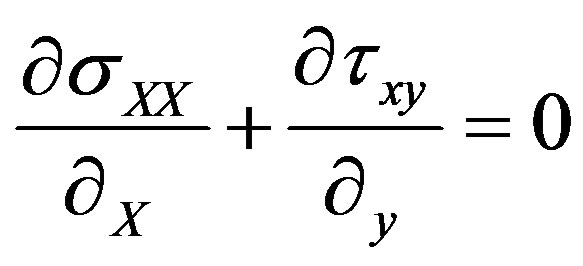 (1)
(1)
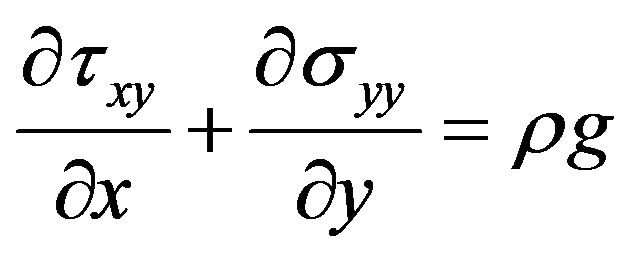 (2)
(2)
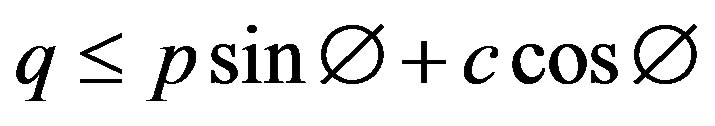 (3)
(3)
where ρ is the density, g the gravity and p and q are the stress invariants.
The stress component expressions below were obtained from an exact analytical solution for the simplified case where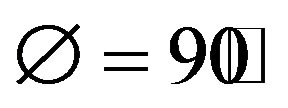 .
.
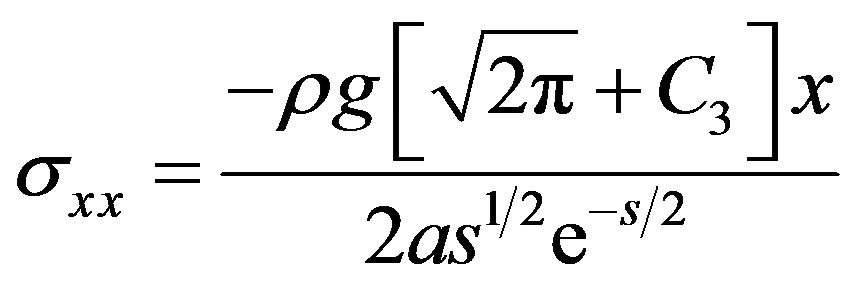 (4)
(4)
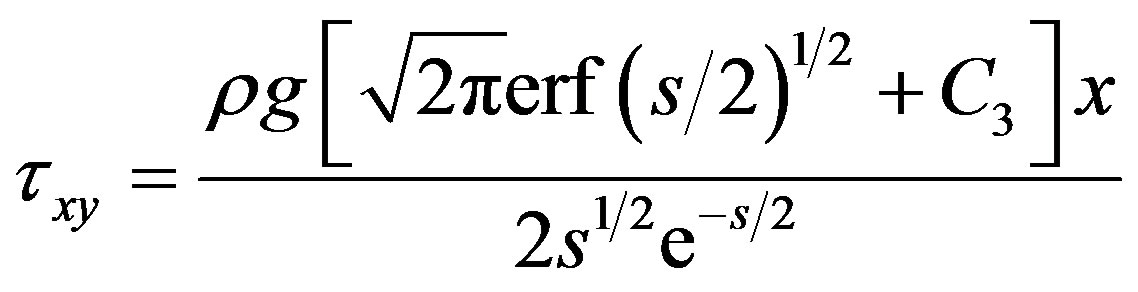 (5)
(5)
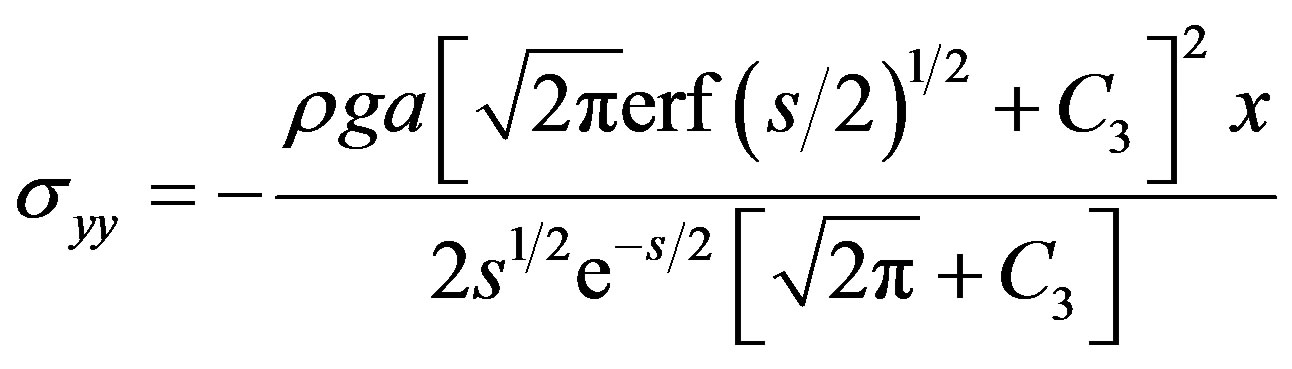 (6)
(6)
where a is the stockpile slope angle,  stands for the error function, s is an integration parameter, b is the slope angle of the straight line that defines the boundary between the two regions and C3 is an integration constant, defined by:
stands for the error function, s is an integration parameter, b is the slope angle of the straight line that defines the boundary between the two regions and C3 is an integration constant, defined by:
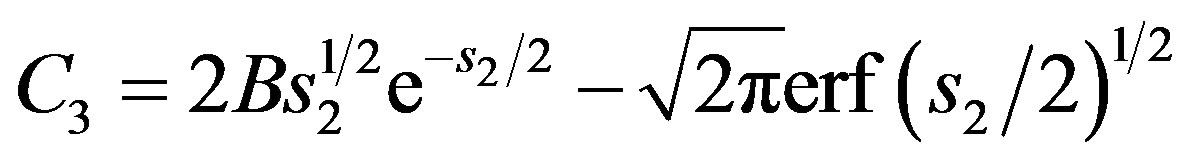 (7)
(7)
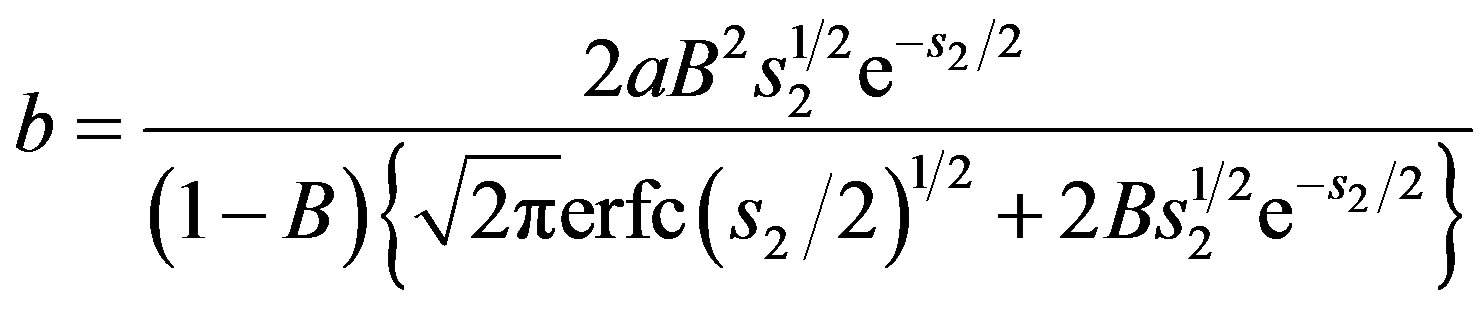 (8)
(8)
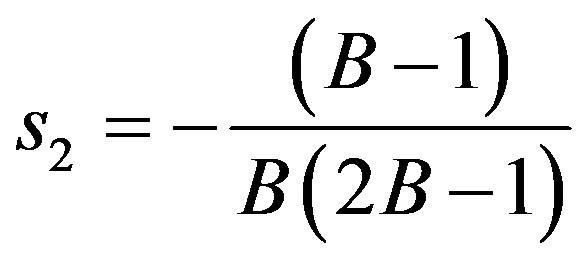 (9)
(9)
s2 is the parametric variable s in the elastic-plastic boundary and erfc(x) is the complementary error function erfc(x) = 1 − erf(x).
This result depends on arbitrary parameter B, which is in the 0.5 < B < 1.0 interval.
The result of these equations is shown in Figure 3 where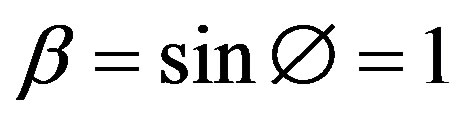 ; the chart also shows the stress distribution obtained [3] for values of β from cosa where a is half the stockpile slope angle up to β = 1.
; the chart also shows the stress distribution obtained [3] for values of β from cosa where a is half the stockpile slope angle up to β = 1.
In the charts in Figure 3, a shift in maximum stress to the edge of the stockpile is noted as the friction angle
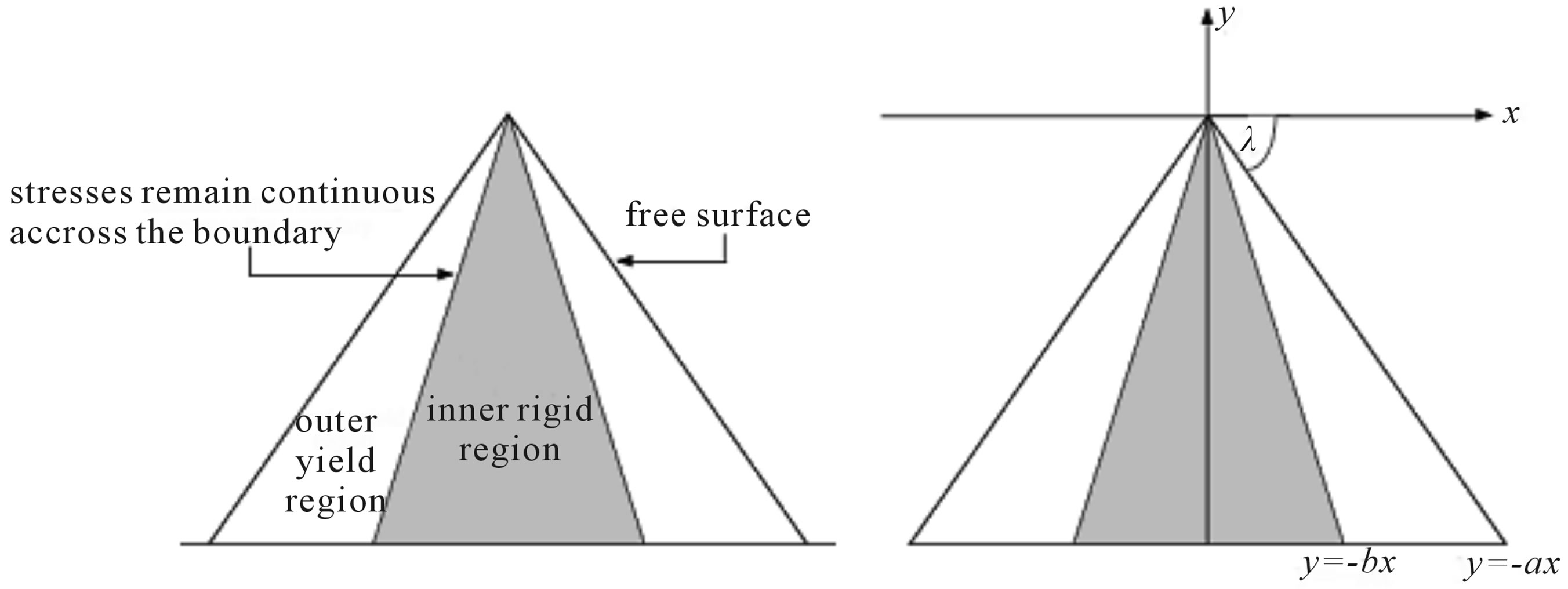
Figure 2. Model of a stockpile consisting of two regions and its system of coordinates [1].
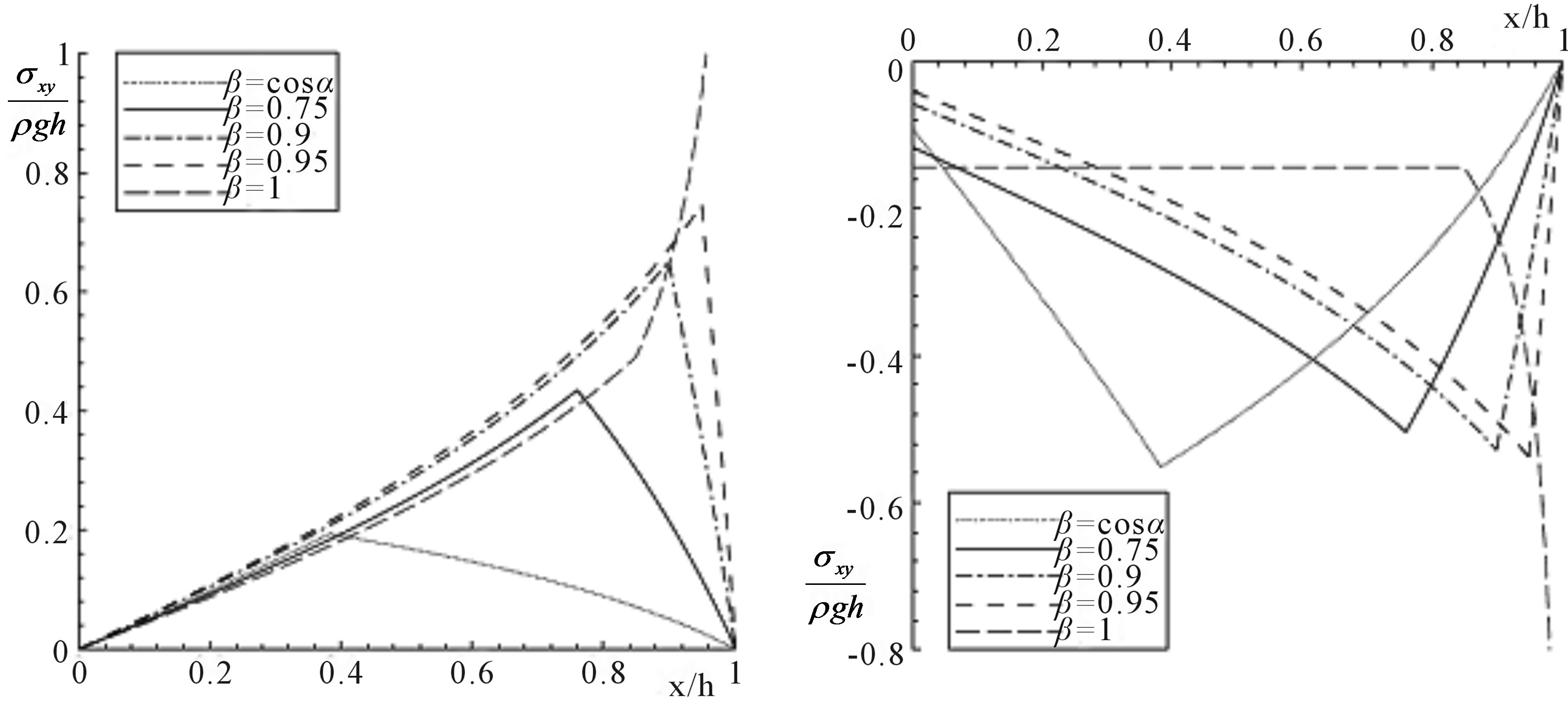
Figure 3. Results obtained analytically for different values of  where α is half the stockpile surface slope angle of inclination [3].
where α is half the stockpile surface slope angle of inclination [3].
increases; apparently stresses tend to infinity on the free surface of the stockpile when the friction angle increases, but stress conversion results in null normal stress at the edge of the stockpile.
In this model it is also possible to associate the boundary between the plastic and elastic regions at the maximum stress point.
The manner in which the material is disposed of affects the central minimum stress value. This stress could be reproduced by the occasional deposition of the material above the material stockpile, and this minimum would disappear if the stockpile was made up of consecutive horizontal layers [1].
An important finding was revealed concerning conically shaped stockpiles of iron ore pellets [4]. The study using the DEM (discrete element method) methodology revealed that the construction of the stockpiles is strongly affected by contact directions and directions of contact forces occurring in the center of the stockpile. The pressures in the central region produce vertical forces as particles make contact when the deposition is distributed throughout the stockpile. When the stockpile is formed by occasional deposition, pressures produce angled forces as particles come into contact, making the stockpile unstable (Figure 4).
The mechanism shaping the stockpile with successive slides as a result of adding material to the crest of the stockpile could affect the grain packing texture, and make the material anisotropic. Slides would trigger a deformation in the same direction they occur in. This is similar to a deformation caused by the material shearing [5].
As the stockpile is shaped by successive slides, the angle of repose of the material could be the maximum inclination angle the material is stable at. For a granular material stockpile, where the grain is dry and slightly compressed, the angle of repose can be considered equal to the friction angle of the material [6]. It is important to note that the frictional nature of granular material is strongly affected by the extent to which the particles are compacted. Imbrication between particles provides additional resistance to shearing. The pure definition of a material friction angle is displayed in Figure 5(a). In Figure 5(b) we can observe high normal rigidity  and low tangential rigidity
and low tangential rigidity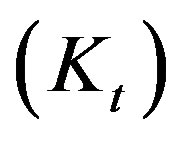 . From another direction, in Figure 5(c) we can observe a higher Kt value and a lower Kn value than in the previous situation [7].
. From another direction, in Figure 5(c) we can observe a higher Kt value and a lower Kn value than in the previous situation [7].
The angle of repose (Figure 6) is also affected by the grain size of particles, since the same material has greater angles of repose for larger particle sizes, with the angularity and flat surfaces of the larger particles offering greater stability [8].
The gaps between the grains may hold some degree of humidity, and depending on moisture content, water surface tension may generate cohesive forces between grains; moreover, when the voids are saturated with water, pore pressure may be enough to separate the particles and cause the mass to liquefy (Figure 7) [8].
3. The Analytical Model Formulated by [1] versus the Iron Ore Fines Stockpile Scale Model
Samples with 50 kg of pellet feed (iron ore fines) were used to form the scale models of the stockpiles set out in the iron ore mine production yards. The density value for the sample is 5.35 g/cm3. This sample was called sample 1 in this article.
We applied the formulation [1] for the geometry of the stockpile used to store pellet feed in mining company yards, h = 12 meters (height) and x = 28 meters (width). The results are shown in Figure 8. The degree of the stockpile slope is 40.6˚ (a = 0.84) and B = 0.75:
For the scale model, the rationale for the experiments was to record through a patented apparatus for recording and treating the stress variation on the axis and on the edge of the stockpile in real time. These continuous records were made during, after and at the stockpile failure.
The scale model of the stockpile in sample 1 is shown in Figure 9. Its base has two lateral retaining walls to simulate the actual conditions the stockpiles undergo in the stockyard.
The results obtained are shown in Figures 10 and 11.
Comparison of the curves obtained in the experiment with models reducing the curves obtained with the analytical formulation finds that curves show the same distribution for the stresses on the axis with the σyy stress as the τxy edge stress. On the σyy axis (vertical stress Figure 10) a fall of this stress can be seen from 0.75 X/h for the theoretical model and 0.78 for the scale model. On the τxy axis (stress at the edge) we have an increase in stress for X/h equal to 0.75 and with the scale model this increase is 0.78. Collecting data with the scale model was not conducive to capturing monotonic data (Figure 11). This fact shows curves with sharp variations for the scale model.
4. Numerical Modeling with PFC 2d
To create numerical models to study the mechanical behaviors of solids based on infinitesimal integration requires mechanical parameters need to be determined. In this particular case studies were based on shear strength.
The shear test consists of applying transverse forces 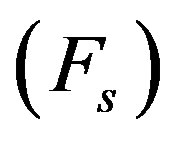 to material being studied and under a constant/steady/continuous normal force
to material being studied and under a constant/steady/continuous normal force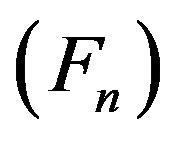 . Results are obtained on a Shear Stress
. Results are obtained on a Shear Stress 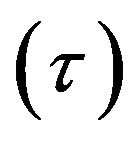 vs. Normal Stress
vs. Normal Stress 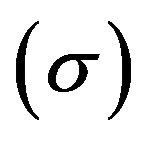 chart (Figure 12). This failure criterion is defined in literature as Mohr-Coulomb’s failure criterion, which enables the friction angle and the cohesion of the material to be determined.
chart (Figure 12). This failure criterion is defined in literature as Mohr-Coulomb’s failure criterion, which enables the friction angle and the cohesion of the material to be determined.
The input parameters in numerical modeling are primarily the angle of friction and rigidity. Rigidity may be defined as the tangent of the ratio of shear stress and normal (vertical) and tangential (horizontal) deformations obtained from samples during the test.
Three tests were performed for each sample, each experiment being subjected to a standard of 50, 200 and 500 kPa. The chart in Figure 13 shows the curve for one of the tests for sample 1.
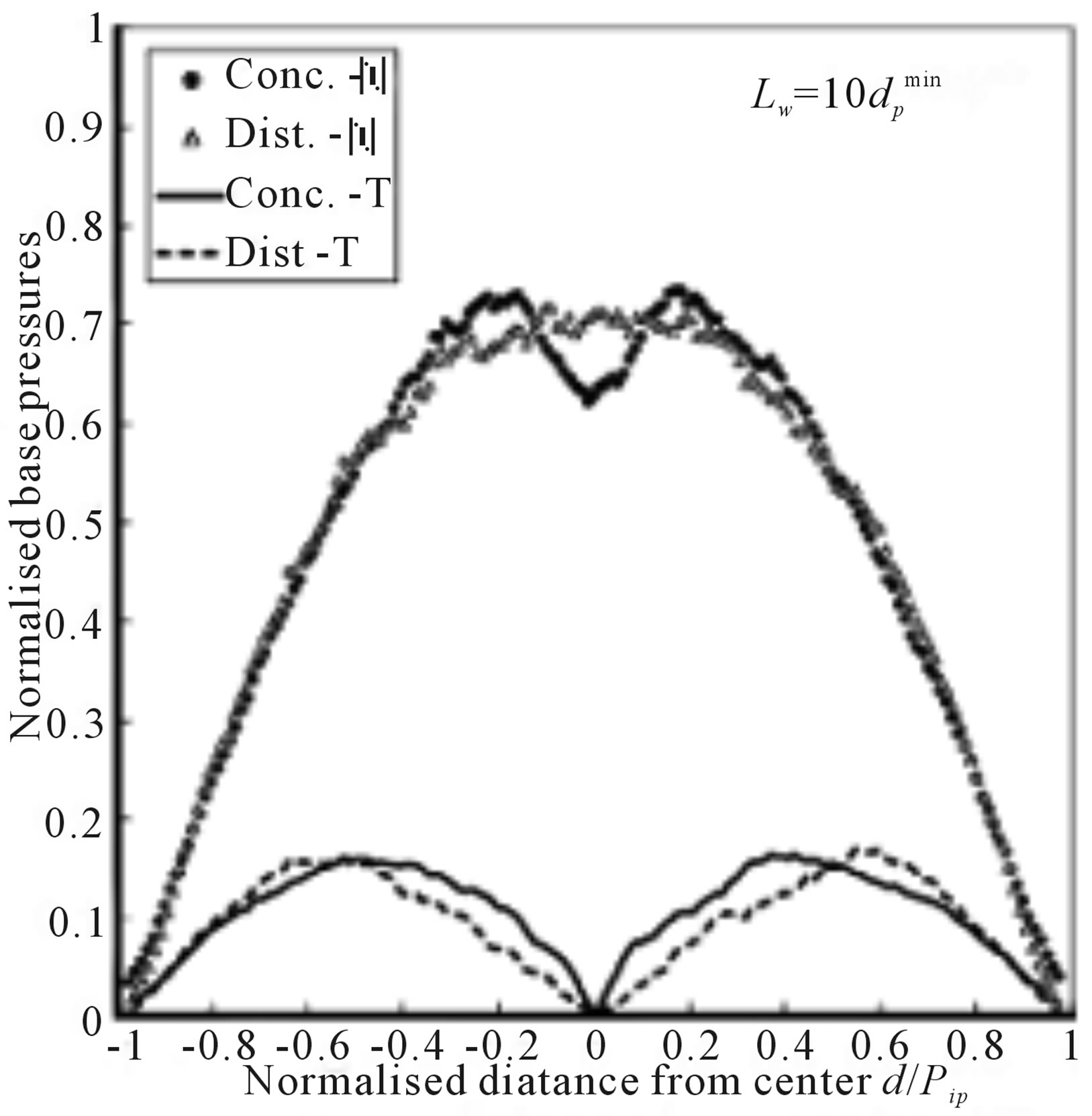
Figure 4. Normalized distribution of pressures depending on the deposition method [4].

Figure 5. Makeup of the friction angle in different conditions (a) pure definition of friction angle, (b) low actual friction angle with ↑Kn, ↓Kt, (c) high actual friction angle with ↓Kn; ↑Kt [7].

Figure 6. Angles of repose of different grain sizes [8].

Figure 7. Negative, null and positive pore pressures, respectively, in the gaps between the particles [8].
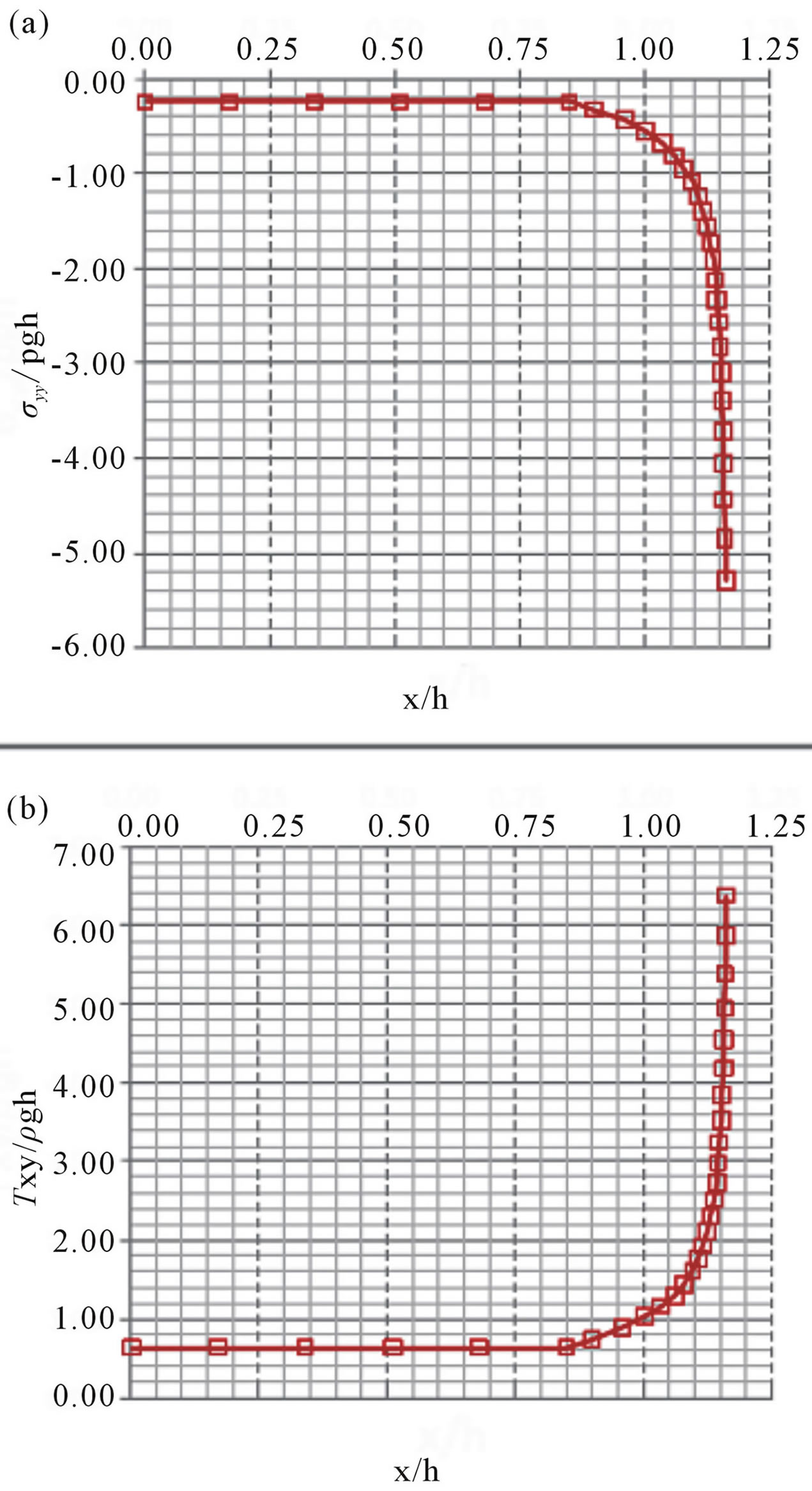
Figure 8. Distribution of (a) vertical stresses, and (b) tangential stresses calculated for the geometry of the stockpile height = 12 meters and width = 28 meters.
The results of the three tests were ploted on a shear stress vs. normal stress chart, and from the Mohr-Coulomb envelope it was possible to calculate the friction angle of the material (Figure 14).

Figure 9. Scale model of an iron ore stockpile.
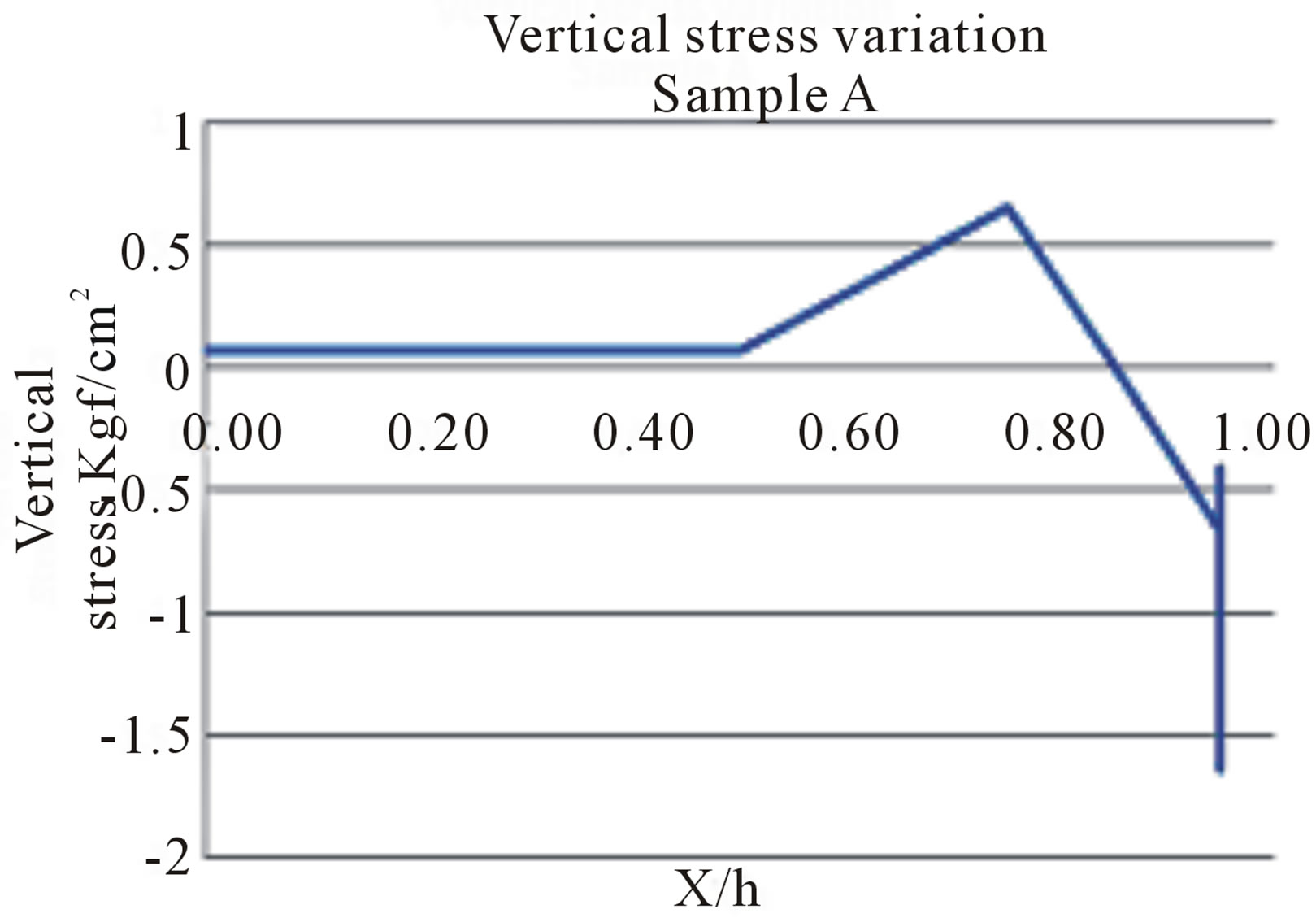
Figure 10. Vertical stress variation according to X/h ratio, with X as the stockpile width and h as its height. Stress variation at the edge of the pile Sample A.
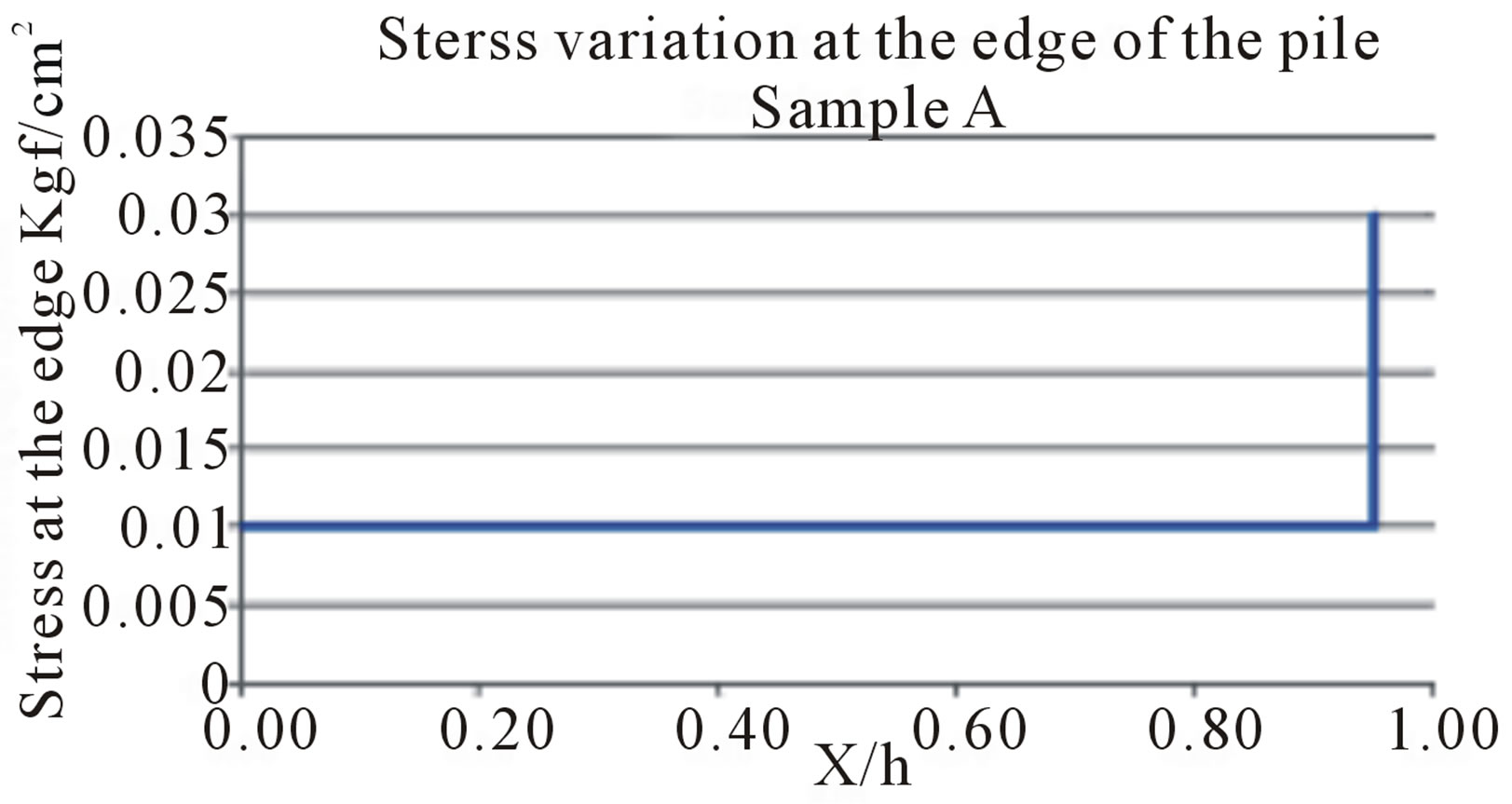
Figure 11. Stress Variation at the edge of the stockpile according to X/h ratio, with X as the stockpile width, and h as its height.
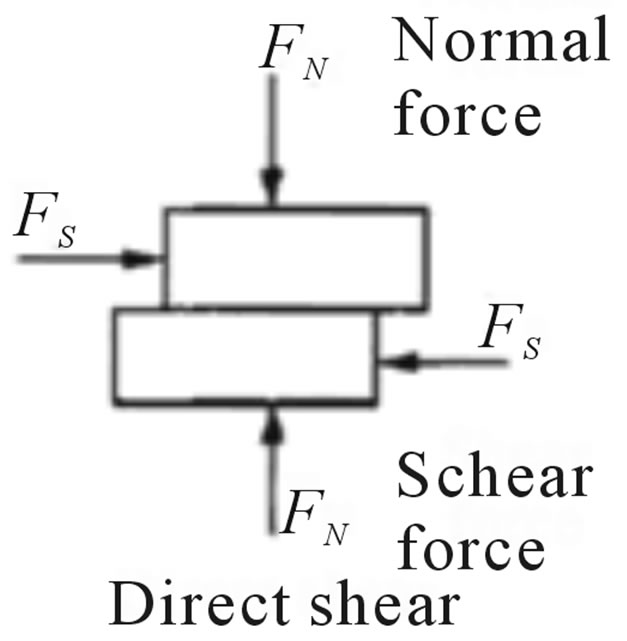
Figure 12. Mechanical application in the shear test.
The results of all the samples are shown in Table 1. The SL sample shows a different behavior compared to

Figure 13. Curve for shear test with sample 1 for normal stress equal to 50 kPa.
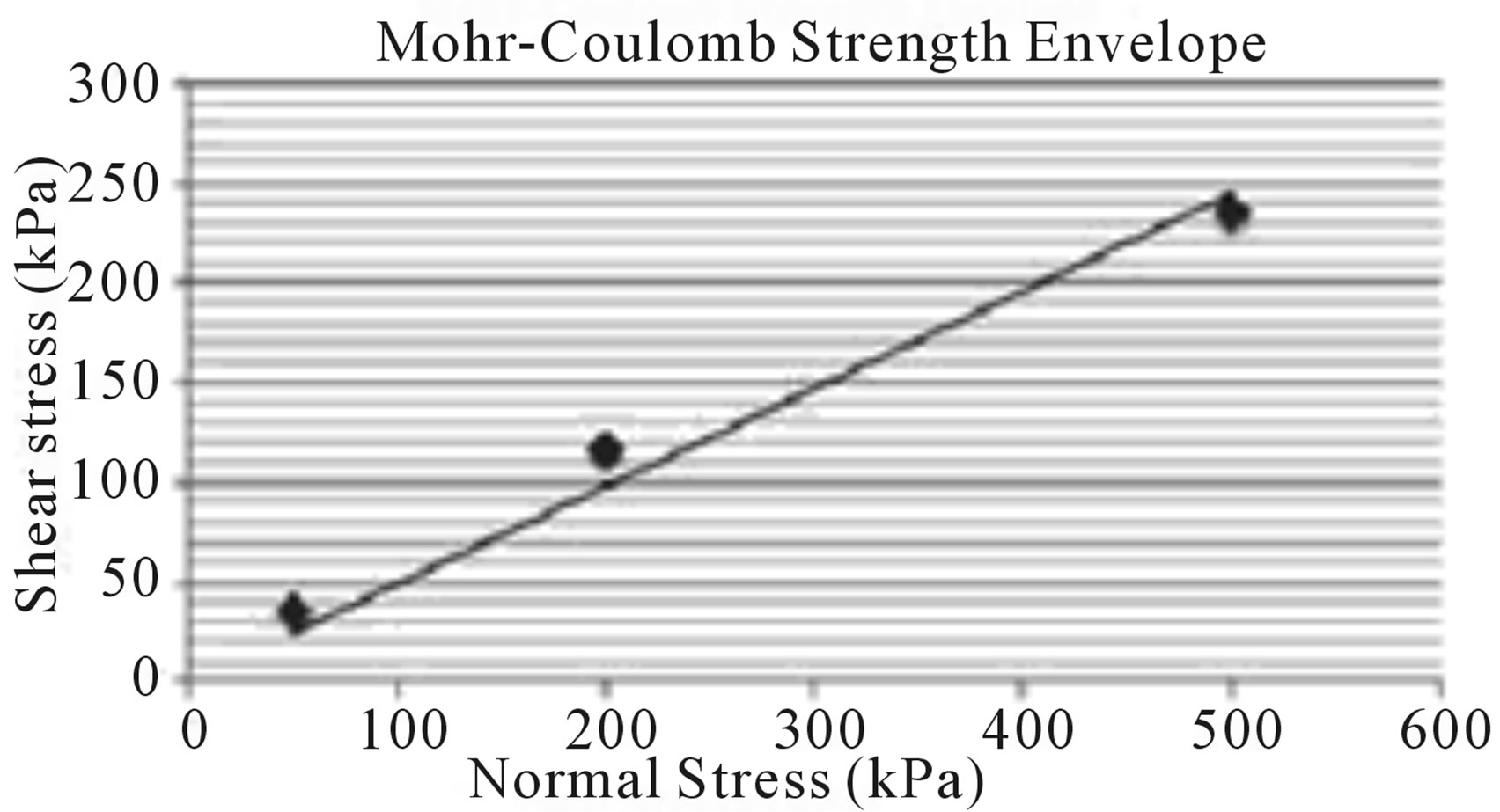
Figure 14. Mohr-Coulomb Envelope for Sample 1.
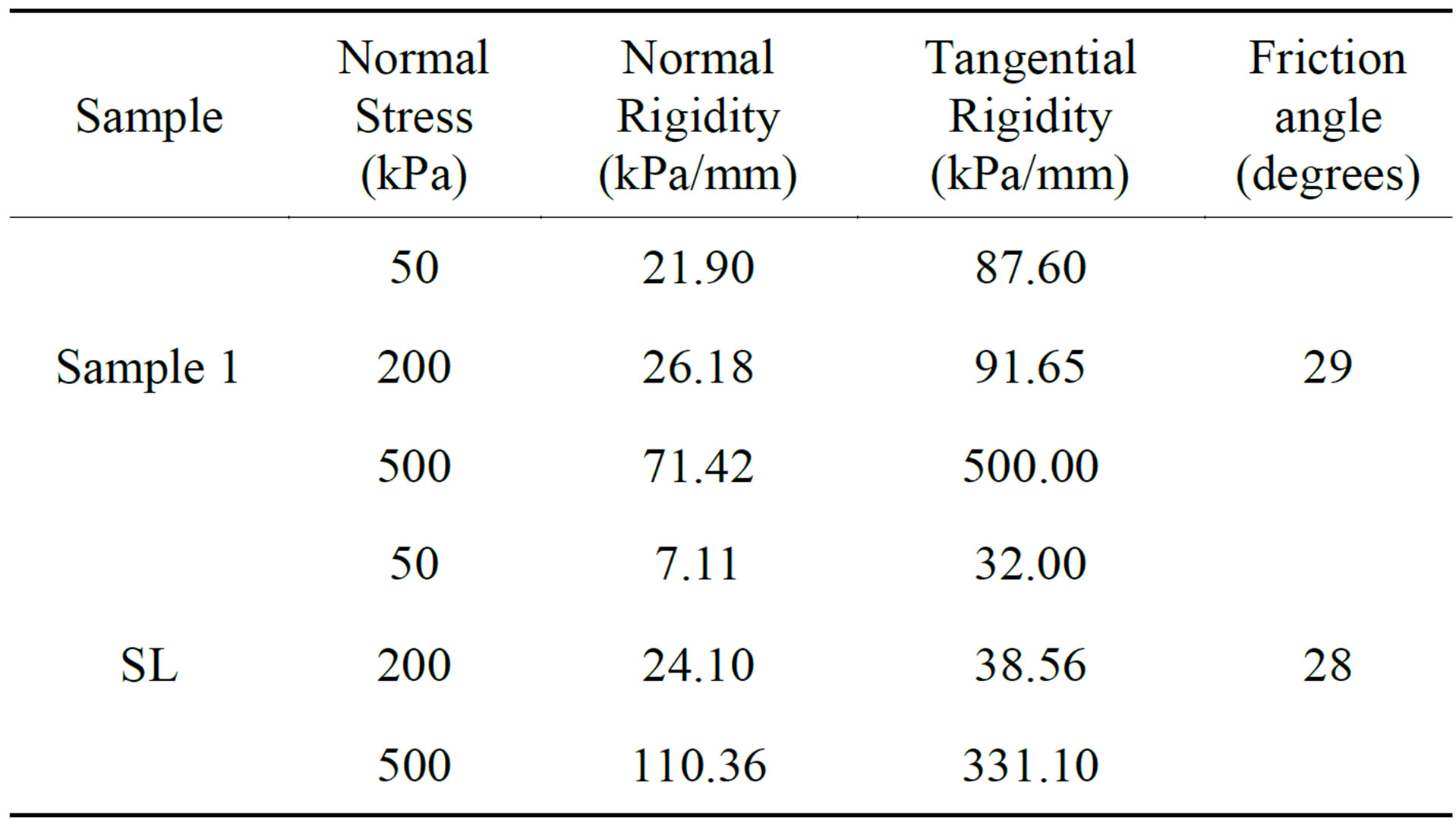
Table 1. Final results of the parameters for numerical modeling.
Sample 1. The most significant factor is the rigidity parameter of the SL sample. This parameter indicates that the vertical rigidity of the SL sample is greater in sample 1, but shear rigidity is smaller. We could infer that the SL stockpiles of ore fines exhibit larger sideway deformations than those along the x axis.
Input parameters and simulations studied.
For the simulations, the following were used:
1) Bulk density, 2.830 kgf/m3
2) Normal and tangential rigidity for normal stress of 500 kPa 3) Friction angle.
The number of particles was 2000, with a stockpile height and width of 12 m and 26 m, respectively, and two lateral retaining walls measuring 1/3 of the height of the stockpile were used.
Figure 15 displays the scheme for monitoring variation in horizontal and vertical forces along the base of the stockpile, represented by points 1, 4, 7, 10 and 13.
The results for the two models are represented as follows:
The forces in blue are compressive forces. We observed the formation of a dome of compression forces enclosed by the green line. A homogeneous compression stress dome is only found for the SL stockpile, where the particles above the dome remain subjected to minor compression stress forces. In the sample 1 stockpile, particles above the green line are “fixed” just by friction force. The effect is that the sample 1 stockpile has a more triangular profile while the SL sample stockpile appears more parabolic (Figure 16).
At no time does the model show a zero velocity for the particles. The particles are always moving even with the stockpile in formation. Stockpiles go as far as the supporting walls, within the number of calculation cycles applied. No overflow of the particles over the wall was seen.
The results of the evolution of vertical and horizontal forces for points 1, 4, and 7 of Figure 15 are depicted in Figures 17-20 respectively. For reasons of symmetry the results for points 10 and 13 (Figure 15) were similar as expected and no charts will be presented for them.
The x-axis corresponds to the number of calculation interaction cycles. At the 2.5 × 106 cycles point, core point 7 of the model in Figure 15 is represented by the blue line. Stabilization forces near 1.0 × 105 N (Y-axis) are seen. Curve fluctuation is noted due to the period of time loading the stockpile. Increase in the stockpile height on reaching these regions of the base used is seen at the beginning of the curves from 4:01 1.0 × 106 cycles and 1.7 × 106 cycles, respectively. Near the left wall (Point 1-Figure 15) the black line shows a tendency towards constant load of 0.2 × 105 N. In position the inter-

Figure 15. Stockpile monitoring regions.
 (a)
(a) (b)
(b)
Figure 16. Results of the numerical model for (a) Sample 1, (b) Sample SL.
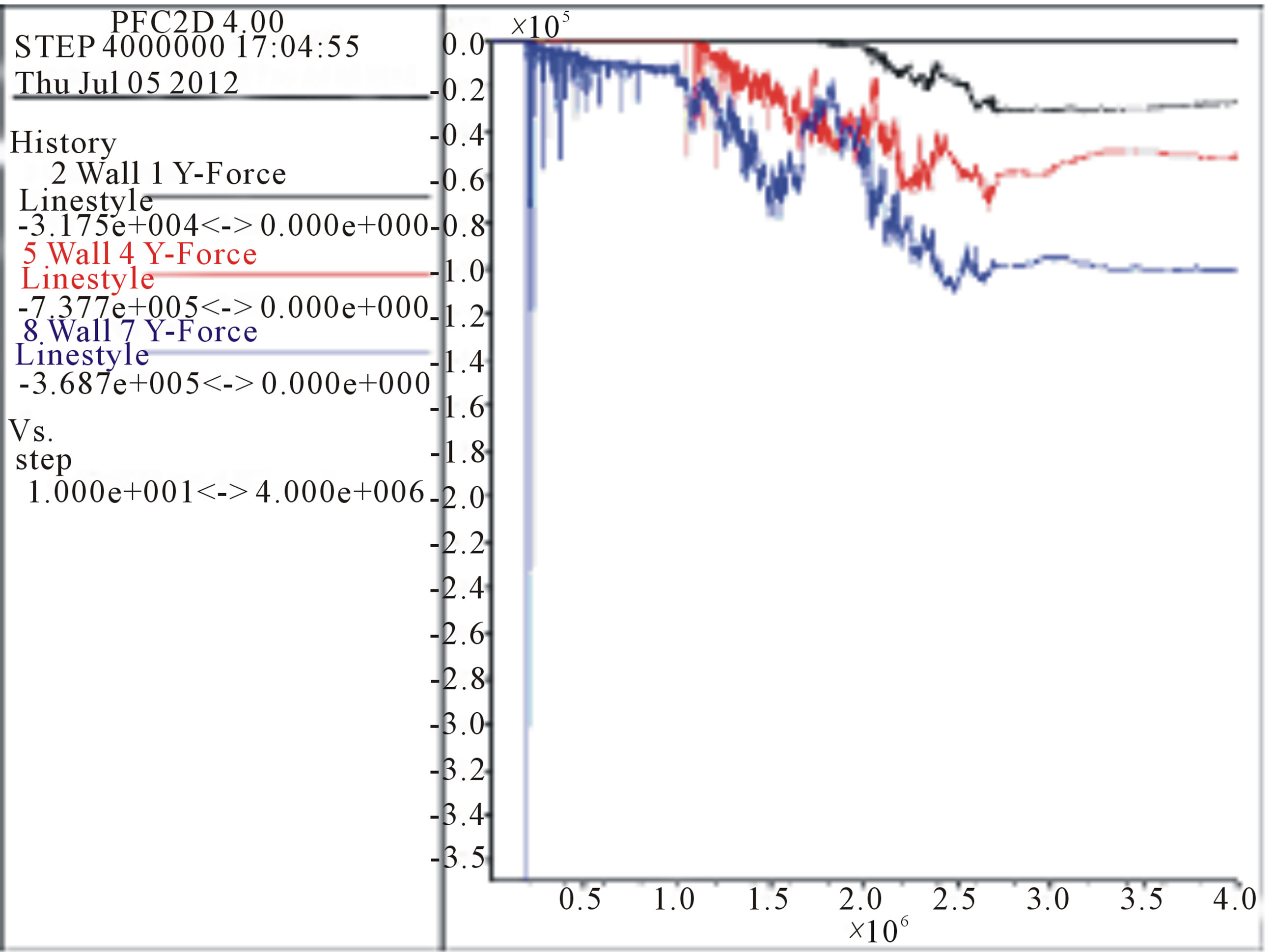
Figure 17. Sample 1 - Evolution of forces towards Y at points 1 (black line), 4 (red line) 7 (midpoint blue line).
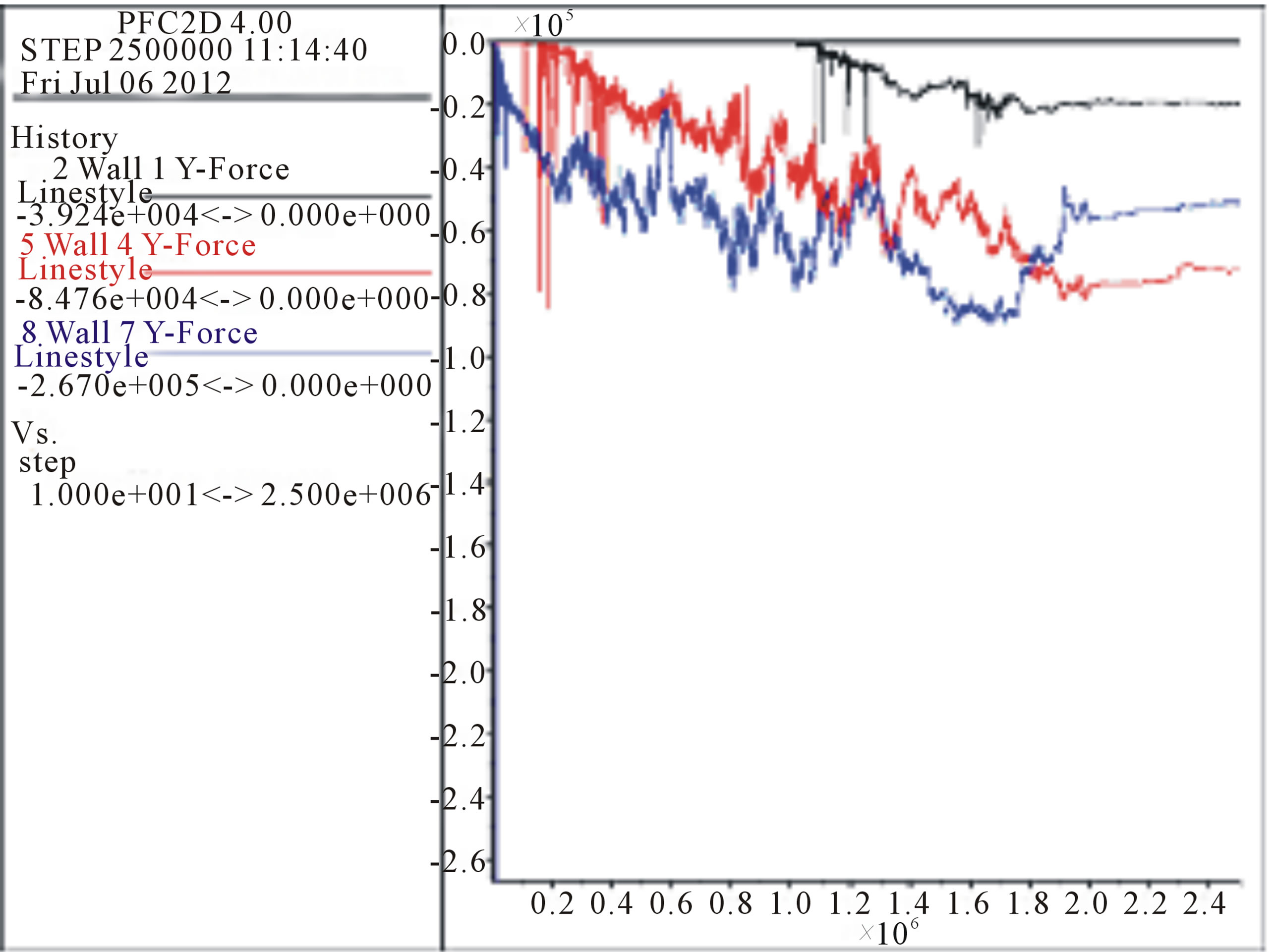
Figure 18. Sample SL - Evolution of forces towards Y at points 1 (black line), 4 (red line) and 7 (blue line midpoint).
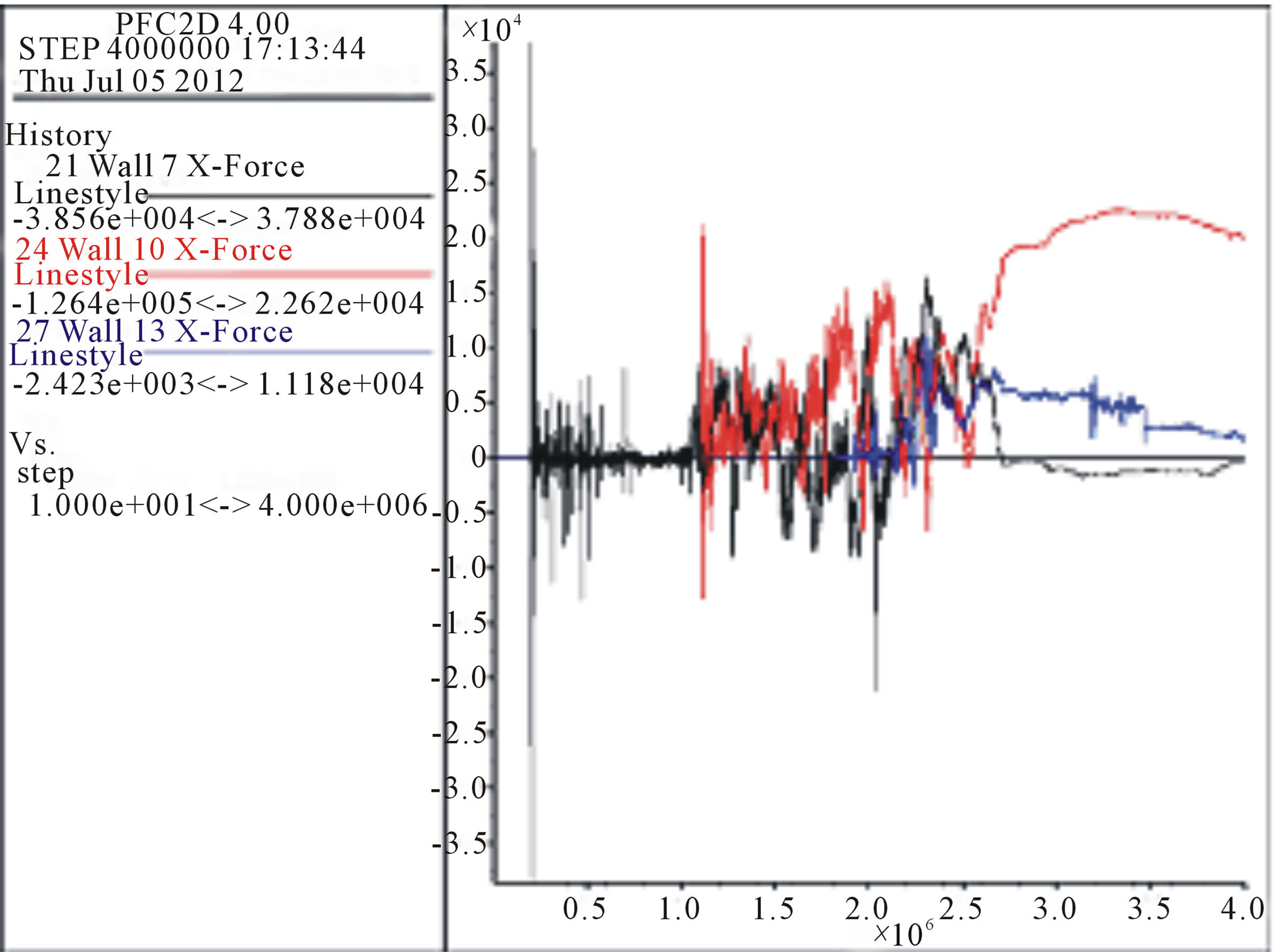
Figure 19. Sample 1 Evolution of forces towards X at points 7 (black line) 10 (red line) 13 (blue line central point).
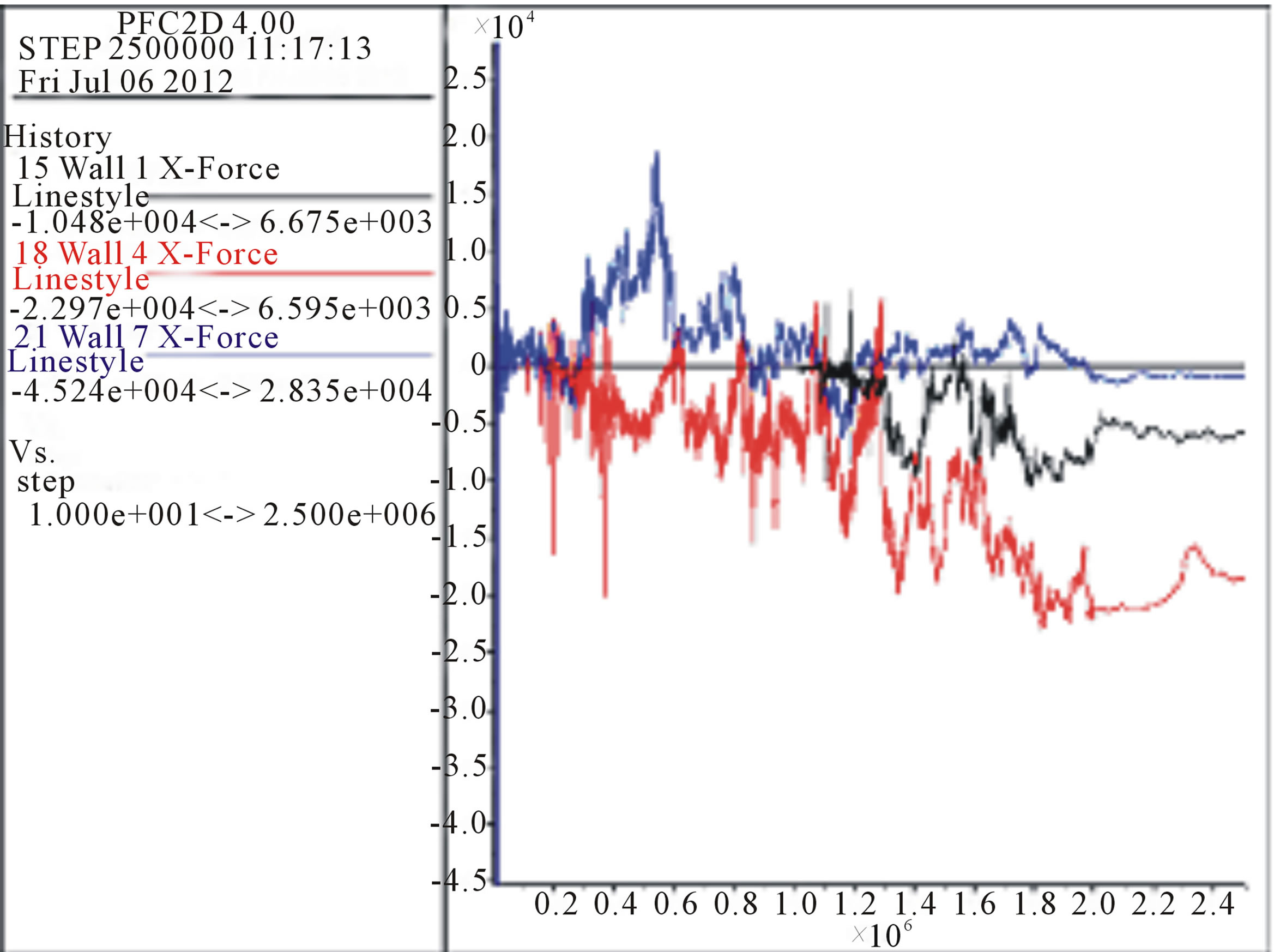
Figure 20. Sample SL - Evolution of forces towards X at points 1 (black line), 4 (red line) and 7 (blue line central point).
mediate red line shows a tendency to stabilize at 4.0 × 106 cycles close to 0.5 × 105 N.
The force at point 1 becomes constant and close to 0.2 × 105 N near the wall where the latter influences the dissipation of part of these forces. At the center point, the tendency to stabilization is very close to the intermediate point after 1.8 × 106 cycles. Forces tend to 0.5 × 105 N for the central axis and 0.9 × 105 N for the intermediate point. These forces remain constant suggesting temporary stabilization of the stockpile.
Point 7 (black line in this case) is the midpoint as shown in Figure 15. A tendency to decompression at 2.5 × 106 cycles is noted. Intermediate points and those close to the wall, 10 and 13 respectively, show a tendency to stabilization, but with different loads for 0.25 × 104 N blue line and red line 2.0 × 104 N.
The central point of the stockpile blue line shows a tendency to cancel out the forces after 2.0 × 106 cycles. The forces at the midpoint and near the wall do not cancel each other out showing a load transfer to these points. This provides certain stability.
5. Final Conclusion
Considerable similarity can be seen on comparing the results of the theoretical analytical model by [1] with the results of the scale model. This resemblance has to do with the function rather than the values. We attributed this to the friction angle of the theoretical model being equal to 90˚. In the scale model this angle is the real angle close to 29˚. Numerical models show similar behavior to each other for the evolution of forces along the X axis; forces eventually stabilize at the edge of the stockpiles. This behavior is observed in the scale model and the model by [1].
On the Y-axis, the theoretical and scale models also show similar functions and different numerical values. The SL numerical model also shows decompression on the central axis of the stockpile, which is not observed in the Sample 1 model.
In Figure 18(b), the center of the SL stockpile shows greater bulk density, indicating a curvature/sagging/archhing/bending characteristic due to smaller tangential rigidity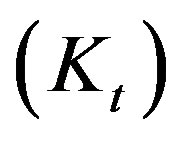 . In the sample 1 stockpile, the center of the pile is less dense and mobile due to the tangential rigidity value being higher. The sample 1 stockpile does not show decompression on the central axis of the stockpile due to the
. In the sample 1 stockpile, the center of the pile is less dense and mobile due to the tangential rigidity value being higher. The sample 1 stockpile does not show decompression on the central axis of the stockpile due to the 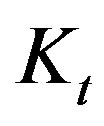 rigidity of the model. The ratio between
rigidity of the model. The ratio between 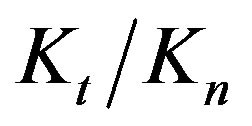 rigidity of sample 1 is approximately 7 and in the SL sample it is 3. This makes the SL stockpile more stable with a parabolic densification format.
rigidity of sample 1 is approximately 7 and in the SL sample it is 3. This makes the SL stockpile more stable with a parabolic densification format.
Acknowledgments
We acknowledge the support from the Foundation Research Grant of the State of Minas Gerais FAPEMIG and National Council for Scientific and Technological Development CNPq and Cia. Vale. We also acknowledge the aid of Germano P. Matias on organizing this paper to its final form.
REFERENCES
- N. Thamwattana, J. M. Hill and G. M. Cox, “Stress distribution in highly frictional granular heaps,” Zeitschrift für angewandte Mathematik und Physik ZAMP, Vol. 55 No. 2, 2004, pp. 330-356. http://dx.doi.org/10.1007/s00033-003-3080-x
- J. Smid and J. Novosad, “Pressure distribution under heaped bulk solids,” Industrial Chemical Engineering Symposium, 1981.
- J. M. Hill and G. M. Cox, “The Force Distribution at the Base of Sand-Piles,” Developments in Theoretical Geomechanics, The John Booker Memorial Symposium, 2000, pp. 43-61.
- J. Ai, J. F. Chen, J. M. Rotter and J. Y. Ooi, “Numerical and Experimental Studies of the Base Pressures beneath Stockpiles,” Granular Matter, Vol. 13, No. 2, 2011 pp. 133-141. http://dx.doi.org/10.1007/s10035-010-0215-6
- A. P. F. Atman, “From the Stress Response Function (Back) to the Sand Pile ‘Dip’,” The European Physical Journal E. Vol. 17, No. 1, 2005, pp. 93-100. http://dx.doi.org/10.1140/epje/i2005-10002-2
- ITASCA Consulting Group. PFC2D User’s Guide. Ver. 4.0. Minneapolis, 2003.
- H. M. O. Hernandez, “Caracterização Geomecânica de Rejeitos Aplicada a Barragens de Aterro Hidráulico,” Dissertação (Mestrado), Universidade de Brasília, 2002.
- F. Press, R. Siever, J. Grotzinger and T. H. Jordan, “Para Entender a Terra,” Tradução RualdoMenegat, 4 Edition, Bookman, Porto Alegre, 2006, 656 p.

