American Journal of Computational Mathematics
Vol.05 No.04(2015), Article ID:61806,5 pages
10.4236/ajcm.2015.54037
A Quadratic Regression Analysis of the Effect of Three Levels of NPK Fertilizer on the Yield of Yellow Maize
Osuolale Peter Popoola1, Kenhide Kazeem Adesanya2, Taiwo Mattew Odusina1, Ayanniyi Wole Ayanrinde3
1Maths & Statistics Department, The Polytechnic, Ibadan, Nigeria
2Statistics Department, Ogun State College of Health Technology, Ijebu Ode, Nigeria
3Mechanical Engineering Department, The Polytechnic, Ibadan, Nigeria

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 30 October 2015; accepted 7 December 2015; published 10 December 2015

ABSTRACT
Fertilizers are essential to modern agriculture; their overuse can have harmful effects on plants, crops and soil quality. Thus, the study seeks to investigate, if (actually) the trio of Nitrogen, Phos- phorus and Potassium (NPK) contribute to the growth and yield of yellow maize, and to determine at what proportion each of the elements is to be applied for optimum yield. Our findings revealed that Nitrogen and Phosphoric fertilizer contributed significantly to the yield of yellow maize while there was no significant effect of Potassium Further analysis on the mean separation of Nitrogen and Phosphorus using Duncan’s Multiple Range Test―(DMRT) showed Nitrogen at 50 kg/ha as signi- ficantly higher than the other levels. For phosphorus, its effect at 20 kg/ha was significantly higher than the other levels. Thus, the derived quadratic model: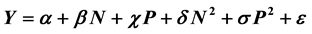 .
.
Keywords:
Factorial Design, NPK Fertilizer, Yellow Maize, Duncan Multiple Range Test, Quadratic Regression

1. Introduction
Fertilizers are essential to modern agriculture; their overuse can have harmful effects on plants, crops and soil quality. Thus, the study seeks to investigate, if (actually) the trio of Nitrogen, Phosphorus and Potassium (NPK) contribute to the growth and yield of yellow maize, and to determine at what proportion each of the elements is to be applied for optimum yield. Statistical method of design of an experiment will be used in the data analysis.
Design of experiment is a structured, organized method that is used to determine the relationship between the different factors (Xs) affecting a process and the output of that process (Y). It is a method of arranging treatments in order that their effects may be meaningfully tested [1] (Wahua, 1999).
The basic concepts of the statistical design of experiments and data analysis were developed in the early part of the 20th century as a cost effective research design tool to help improve yields in farming. Since then, many types of designed experiment and analysis techniques have been developed to meet the diverse needs of researchers [2] (Cochran and Cox, 1957). In building a design according to [3] Larsen, P. V (2006), there is four interrelated steps to follow which includes.
1) Define an objective to the investigation, e.g. better understand or sort out important variables or find optimum.
2) Define the variables that will be controlled during the experiment (design variables), and their levels or ranges of variation.
3) Define the variables that will be measured to describe the outcome of the experimental runs (response variables), and examine their precision.
4) Among the available standard designs, choose the one that is compatible with the objective, number of design variables and precision of measurements, and has a reasonable cost.
The design variables that will be measured are the various levels of fertilizers application to yellow maize i.e. N25P0K0, N50P10K60, N75P20K120.
Yellow Maize and Fertilizers
Fertilizer, natural or synthetic chemical substance or mixture, used to enrich soil so as to promote plant growth. Plants do not require complex chemical compounds analogous to the vitamins and amino acids required for human nutrition, because plants are able to synthesize whatever compounds they need. They do required more than a dozen different chemical elements and these elements must be present in such forms as to allow an adequate availability for plant use. Within this restriction, Nitrogen, for example, can be supplied with equal effectiveness in the form of urea, nitrates, ammonium compounds, or pure ammonia.
Virgin soil usually contains adequate amounts of all the elements required for proper plant nutrition. When a particular crop is grown on the same parcel of land year-after-year, however, the land becomes exhausted of one or more specific nutrients. If such exhaustion occurs, nutrients in the form of fertilizers must be added to the soil. Plants can also be made to grow lushly with suitable fertilizers. Of the required nutrients, hydrogen, oxygen and carbon are supplied in inexhaustible form by air and water. Sulfur, calcium and iron are necessary nutrients that usually are present in soil in ample quantities. Lime (calcium is often added to soil, but its function is primarily to reduce acidity and not, in the strict sense, to act as a fertilizer. Nitrogen is present in enormous quantity in the atmosphere, but plants are not able to use Nitrogen in this form; bacteria provide Nitrogen from the air to plants of the legume family through a process called Nitrogen fixation. The three elements that most commonly must be supplied in fertilizers are Nitrogen (N), Phosphorous (P) and Potassium (K). Certain other elements, such as boron, copper and manganese sometimes needed to be included in small quantity.
Fertilizers are essential to modern agriculture, their overuse can have harmful effects on plants, crops and on soil quality. In addition, the leaching of nutrients into bodies of water can lead to water pollution such as eutrophication, by causing excessive growth of vegetation. Hence, the studies aimed at investigating, if actually, the trio of Nitrogen, Phosphorus and Potassium (NPK) contribute to the growth and yield of yellow maize; to detect which of the three elements of NPK contribute most. It does further to determine at what proportion each of the three elements is to be applied for optimum yield and if applied correctly, confirm the optimum yield at kilogram per hectare. Three levels of NPK was applied on yellow maize: N25P0K0, N50P10K60, N75P20K120.
In a recent research carried out in Hungary by [4] Dr. Pete Pepo three levels of Nitrogen, Phosphorus, and Potassium were used as follow: N0P0K0, N60P45K45, N240P180K180. In his finding, it shows that Nitrogen at 60 kg, Phosphorus at 45 kg and Potassium at 45 kg would be preferable for higher yield than the other levels used in the study [4] . Peter Pepo.
In another research work carried out in Pakistan, which was published in Pakistan [5] Journal of Science (Vol. 62 No. 4 December, 2010). Titled: Growth and yield of maize (Zea mays L.) Cultivars affected by NPK Application in different proportion. Four levels of NPK fertilizer was used. The result shows that f2 (N175P80K60) gives optimum yield than the other levels.
Nutrient Deficiency in Plant: Plants, like human beings need the right nutrition to remain healthy. If they do not get enough of a nutrient, the symptoms show-up in the general appearance as well as in colours of plant. Nutrient deficient plants are often stunted (small) and the leave have a pale green color, yellowish or reddish spotting or stripping. Yields are reduced, sometimes severely.
2. Materials and Methods
2.1. The Research Design: Factorial Experiments
Montgomery (1976) [6] defined factorial experiments as experiment in which each complete trial or replication of the experiment and all possible combinations of the level of the factors are investigated. This is the most efficient design when an experiment requires a study of the effects of two or more factors. When factors are arranged in a factorial experiment, they are often said to be crossed
Factorial experiments are more efficient than one factor at a time experiments. This design is necessary when interactions may be present, to avoid misleading conclusions. It allows effects of a factor to be estimated at several levels of the other factors, yielding conclusions that are valid over a range of experimental conditions [7] (Anbari and Lucas, 1994).
2.2. Factorial Design Experiment
This was chosen because it is the most suitable for any experiment that is more than one factor. Factorial design is also been employed in order to evaluate the effect of each factor, the combination of the three and the interaction effect. In this paper, each of the three factors is at three level i.e. 3 ×3 factorial experiment.
The General Statistical Model for the 3-Factorial Design is:
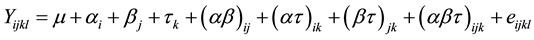
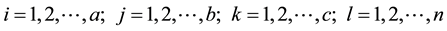
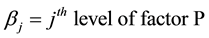
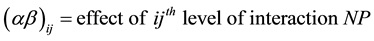
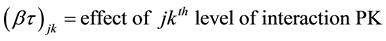
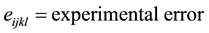
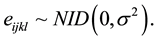
2.3. The Mean Separation
The F-test for any testable effect in the analysis of variance (ANOVA) table may indicate significant differences or otherwise [8] Neave, H. R. (1981). When significant, it suggests that, at least, one pair of the means in question must be different [1] (Wahua, 1999). Statistical significance implies that whatever difference we are referring to, is too big to be attributed to experimental error. It is real; not a chance event. However, the F-test did not tell us which means actually differed. We have to set-up a criterion of measurement to find out how different a difference should be before it is declared statistically significant [9] Montgomery, D. C. (2005).
Duncan’s Multiple Range Test (DMRT)
Duncan purposely developed this method to reduce experiment wise error rate.
DMRT has the advantage of pair wise comparison and takes into account the number of treatments. However, it is very cumbersome to calculate when the means are many and has different values to be considered.
In a case where there are many effects and their interaction to be tested the objective is to know the most significant level(s) that will have maximum perception. Duncan’s Multiple Range Test is the appropriate test to detect the most significant level.
2.4. Determinations of Optimum Levels of the Factor Effects Using Quadratic Regressions
The derived model is 
3. Results and Discussion
After the data have been subjected to statistical analysis using spss (statistical package) version 11.0 the ANOVA table (Table 1) shows the following results.
It shows that the effects of Nitrogen at 50 kg/ha are more significant than Nitrogen at 75 kg/ha and at 25 kg/ha. Therefore, Nitrogen contributed more to the Yield of maize at 50 kg level of quantities. Also for phosphorus, the effect of Phosphorus at 20 kg/ha is more significant than Phosphorus at 0 kg/ha and 10 kg/ha Therefore, phosphorus contributed more to the yield of maize at 20 kg level of quantities.
This leads us to find the optimum levels for the application of fertilizers which gives optimum yield of maize. Through the application of regression analysis, it was revealed that application of nitrogen at 57.7 kg/ha and phosphorus at 27.4 kg/ha gave the optimum yield of maize. If we applied nitrogen and phosphorus at the optimum yield we are expected to have a maximum yield of 39.05724 tons
With the outcome of the analysis, it is obvious that both the Nitrogen and Phosphorus played an important role on the yield of maize if applied in the right proportion. For maximum yield of 39.05724 tons of maize, nitrogen should be applied at 57.7 kg/ha and phosphorus at 27.4 kg/ha .It is important to note that there is no interaction effects between the three main effects of N, P and K. It is therefore recommended that Federal Government should support farmers in the area of given subsidies to farmers so as to procure fertilizers at a cheaper price and educate farmers on the application of fertilizer in the right proportion to give optimum yield of maize.
The analysis performed showed that fertilizer has a contributory role in the yield of maize. And in particular that certain levels of Nitrogen and Phosphorus will give optimum yield of maize. However, it was also found that the theoretical optimum level of phosphorus (that is 27 kg/ha) was not used in the experiment. Hence, it will be recommended that a further research be carried out where the levels of phosphorus will be increased to 45 kg. This will help to ascertain the actual optimum of phosphorus.
4. Conclusions
This research work is an attempt to develop a quadratic regression model of the effect of three levels of NPK fertilizer on the yield of yellow maize. The study also seeks to investigate if actually, the trio of Nitrogen, Phosphorus and Potassium (NPK) contribute to the growth and yield of yellow maize; also to detect and investigate which of the three elements of NPK contribute most. It does further to determine at what proportion each of the three elements is to be applied for optimum yield and if applied correctly, confirm the optimum yield at kilogram per hectare.
The result of the Analysis of Variance (ANOVA) carried out showed that Nitrogen and Phosphoric fertilizer contributed significantly to the yield of yellow maize while there was no significant effect of Potassium.
A further analysis on the mean separation of Nitrogen and Phosphorus using Duncan’s Multiple Range Test― (DMRT) (Table 2 and Table 3) showed that the effect of Nitrogen at 50 kg/ha was significantly higher than
Table 1. Analysis of variance (anova) table.
Table 2. Phosphorus mean yield.
Table 3. Nitrogen mean yield.
Nitrogen at 75 kg/ha and at 25 kg/ha (Table 2). Also for phosphorus, its effect at 20 kg/ha was more significantly higher than Phosphorus at 0 kg/ha and 10 kg/ha (Table 3). Thus, the model:

Hence the optimum levels for the application of fertilizers which gives optimum yield of yellow maize were obtained through the application of the model. It was revealed that application of nitrogen at 57.7 kg/ha and phosphorus at 27.4 kg/ha give the optimum yield of yellow maize of 39.05724 tons kg/ha.
Cite this paper
Osuolale PeterPopoola,Kenhide KazeemAdesanya,Taiwo MattewOdusina,Ayanniyi WoleAyanrinde, (2015) A Quadratic Regression Analysis of the Effect of Three Levels of NPK Fertilizer on the Yield of Yellow Maize. American Journal of Computational Mathematics,05,426-430. doi: 10.4236/ajcm.2015.54037
References
- 1. Asghar, A.A., Syed, W.H., Asif, M., Khaliq, T. and Abid, A.A. (2010) Growth and Yield of Maize (Zea mays L.) Cultivars Affected by NPK Application in Different Proportion. Pakistan Journal of Science, 62.
- 2. Anbari, F.T. and Lucas, J.M. (1994) Super-Efficient Designs: How to Run Your Experiment for Higher Efficiency and Lower Cost. ASQC Technical Conference Transactions, 852-863.
- 3. Cochran, W.G. and Cox, G.M. (1957) Experimental Design. Willy International Publication.
- 4. Larsen, P.V. (2006) Module 12: Factorial Experiments. Master of Applied Statistics.
- 5. Pepo, P. (2010) Effect of NPK Fertilization, Irrigation and Crop Rotation on the Yield of Maize Hybid.
- 6. Montgomery, D.C. (1974) Design and Analysis of Experiments. John Wiley & Sons Incorporation, New York.
- 7. Montgomery, D.C. (2005) Design and Analysis of Experiments. 6th Edition, John Wiley & Sons, New York.
- 8. Neave, H.R. (1981) Elementary Statistical Tables for All Users of Statistic.
- 9. Wahua, T.A.T. (1999) Applied Statistics for Scientific Studies. Macmillan Publishing, Lagos.


