American Journal of Computational Mathematics
Vol.05 No.02(2015), Article ID:56458,5 pages
10.4236/ajcm.2015.52006
Theories and Analyses Thick Hyperbolic Paraboloidal Composite Shells
Mohammad Zannon*, Basma Al-Shutnawi, Hussam Alrabaiah
Department of Mathematics, Tafila Technical University, Tafila, Jordan
Email: *zanno1ms@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 March 2015; accepted 17 May 2015; published 20 May 2015
ABSTRACT
This paper presents the stress resultants of hyperbolic paraboloidal shells using higher order shear deformation theory recently developed by Zannon [1] -[3] . The equilibrium equations of motion use Hamilton’s minimum energy principle for a simply supported cross-ply structure by Zannon (TSDTZ) [2] [3] . The results are calculated for orthotropic, two-ply unsymmetrical [90/0] shells. The extensional, bending and coupling stiffness parameters are calculated using MATLAB algorithm for laminated composite hyperbolic paraboloidal shells. A comparison of the present study with other researchers in the literature is given, and is in good agreement.
Keywords:
Stress Resultants, Hyperbolic Paraboloidal, Hamilton Principles, Thick Shell, Third Order Shear Deformation, Cross-Ply, Stiffness Matrix

1. Introduction
The main objective of shell theory is to predict the stress and the displacement arising in an elastic shell in response to given forces. Such a prediction is made either by solving a system of partial differential equations or by minimizing a functional, which may be defined either over a three-dimensional set or over a two-dimensional set, depending on whether the shell is viewed in its reference configuration as a three-dimensional or as a two- dimensional body. The three-dimensional theory of shells is obtained simply by replacing the reference configuration of a general body with that of a shell [2] -[4] .
Tow formulations are used to show equations of motion with required boundary conditions for doubly curved deep thick composite [5] -[7] . The first is based upon the formulation that is presented initially by Reddy [8] . The second formulation is based upon that of Qatu [1] [9] . Qatu considers the radius of twist in his formulation.
The vibration of thick shells has been solved using the first order shear deformation shell theory [5] -[10] . Three dimensional theory of elasticity is used for solving theories of shell structures. Thus three dimensional analyses of shells are considered to be the most accurate.
This paper presents Stress resultants becuase hyperbolic paraboloidal shells are determined by deriving the dynamic stiffness matrix from the equilibrium equations of motion using Hamilton’s minimum energy principle for a simply supported cross-ply structure by Zannon (TSDTZ) [2] -[4] . The results are calculated for orthotropic. The extensional, bending and coupling stiffness parameters are calculated using a commercial software package (ANSYS). In this formulation, the stiffness parameters are calculated using exact integration (and/or terms truncated to a specific order) of stress resultant equations. In addition, Zannon [2] -[4] considers the radius of twist in formulation. The third order polynomials for in-plane displacements in the z-direction are utilized allowing for the inclusion of shear deformation and rotary inertia effects (Third order shear deformation theory or (TSDTZ) [2] -[4] .
Exact static and free vibration solutions for isotropic and symmetric and anti-symmetric cross-ply hyperbolic shells for different length-to-thickness and length-to-radius ratios are obtained using the above theories. Results of both theories are compared with those obtained using a three-dimensional (3D) analysis to test the accuracy of the shell theories presented here. Early treatment of composite thick shells (e.g. [5] [11] ) includes both shear deformation and rotary inertia rotary but fails to include accurate representation of curvature (the z/R terms in the stress resultants).
2. TSDTZ Shell Theory
The approximation of displacement components using the third-order shear deformation shell theory can be written as Zannon (TSDTZ) [2] .
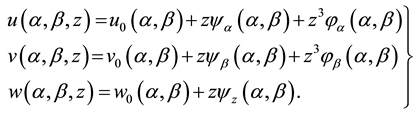
where 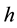 is the shell thickness and
is the shell thickness and ,
,  ,
,  ,
, 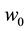 are mid-surface displacements of the shell and
are mid-surface displacements of the shell and ,
, 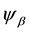 ,
,  are mid-surface rotations and
are mid-surface rotations and ,
, 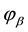 are higher order terms rotation of transverse normal.
are higher order terms rotation of transverse normal.
Equation (1) constitutes the only assumption needed to reduce 3D elasticity equations in curvilinear coordinates to the shell theory by Zannon [2] [3] . The strain-displacement Relationships in the principal coordinates of a doubly-curved shell are given in [2] [3] . The stress resultant or the stiffness matrices are given in [2] [3] . Substituting these stiffness parameters in the Hamilton equation [1] -[5] and simplifying the resulting equations, we get the equations of motion and boundary conditions for S2 are given in [2] [3] .
3. Equation of Motion
Let us consider the Hyperbolic laminated shell as shown in Figure 1 with length 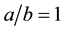 under load per unit area,
under load per unit area, 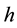 is the thickness of the shell. If the load is orthogonal to the surface, then Lame’ parameters (elastic and
is the thickness of the shell. If the load is orthogonal to the surface, then Lame’ parameters (elastic and
shear modulus) of middle surface 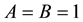 and
and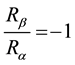 ,
, 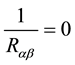 are substituted in moment and force re-
are substituted in moment and force re-
sultants [1] -[3] [9] to formulate the Hyperbolic shell equations for TSDTZ. The moment and force resultant equations are given in [2] [3] . The stress resultant terms are shown in Figure 1.
Therefore, the displacement mid surface for hyperbolic paraboloidal thick shells is rewritten as [2] [3] :
Figure 1. Surface to force and moment resultants of shell form composite structures [1] -[3] .
Thus, the Equations of motion (2) for hyperbolic paraboloidal thick shells reduces to [2] [3]
4. Numerical Results and Discussion
To validate the third order shear deformation theory, the values of extensional


nated composite Hyperbolic thick shells. Thenit is compared with the first order shear deformation theory from the literature. There are small discrepancies are seen in the Tables 1-3, which is due to the third order shear deformation and the tolerance limitations. Tables 1-3 show the extensional stress, coupling, and bending stiffness parameters for [0/90] laminated hyperbolic thick shells. While comparing the various stiffness parameters with the existing literature and the present theory [1] -[5] [8] -[11] , we see that the TSDTZ approximation is more accurate in in comparison with first order shear deformation theory.
5. Summary and Conclusion
TSDTZ offers a more accurate representation of the stiffness parameters and the stress resultant equations. Most analyses performed here show that there is an improvement obtained when TSDTZ is used. Also, TSDTZ offers
Table 1. Non-dimensional extensional stiffness matrix for 










Table 2. Non-dimensional coupling stiffness matrix for 










Table 3. Non-dimensional bending stiffness matrix for 










many other advantages in the accurate representations such as extensional, coupling, and stress stiffness para- meters, as shown in Tables 1-3 and is mainly due to the inclusion of the term 
References
- Qatu, M., Zannon, M. and Mainuddin, G. (2013) Application of Laminated Composite Materials in Vehicle Design: Theories and Analyses of Composite Shells. SAE International Journal of Passenger Cars-Mechanical Systems, 6, 1347-1353. http://dx.doi.org/10.4271/2013-01-1989
- Zannon, M. and Qatu, M. (2014) Mathematical Modeling of Transverse Shear Deformation Thick Shell Theory. International Journal of Engineering Research and Management (IJERM), 1.
- Zannon, M. and Qatu, M. (2014) Free Vibration Analysis of Thick Cylindrical Composite Shells Using Higher Order Shear Deformation Theory. International Journal of Engineering Research and Management (IJERM), 1.
- Zannon, M. (2014) Free Vibration of Thin Film Cantilever Beam. International Journal of Engineering and Technical Research (IJETR), 2.
- Love, E. (1892) A Treatise on the Mathematical Theory of Elasticity. 4th Edition, Cambridge University Press, Cambridge; Dover Publishing, New York.
- Leissa, A.W. (1993) Vibration of Shells. US Government Printing Office, Washington DC. Reprinted by the Acoustical Society of America.
- Timoshenko, S. and Woinowsky-Krieger, S. (1959) Theory of Plates and Shells. New York.
- Lee, S.J. and Reddy, J.N. (2004) Vibration Suppression of Laminated Shell Structures Investigated Using Higher Order Shear Deformation Theory. Smart Materials and Structures, 13, 1176-1194. http://dx.doi.org/10.1088/0964-1726/13/5/022
- Qatu, M.S., Sullivan, R.W. and Wang, W. (2012) Review of Recent Literature on Static Analyses of Composite Shells: 2000-2010. Journal of Composite Materials, 2, 61-86. http://dx.doi.org/10.4236/ojcm.2012.23009
- Deana, C.E. and Werbya, M.F. (1992) Hamilton’s Principle and the Equations of Motion of an Elastic Shell with and without Fluid Loading. Computational and Applied Mathematics, 92, 131-140.
- Asadia, W., Wanga, W. and Qatu, M.S. (2012) Static and Vibration Analyses of Thick Deep Laminated Cylindrical Shells Using 3D and Various Shear Deformation Theories. Composite Structures, 94, 494-500. http://dx.doi.org/10.1016/j.compstruct.2011.08.011
- Qatu, M.S. (2004) Vibration of Laminated Shells and Plates. Elsevier, Oxford.
Nomenclature
NOTES
*Corresponding author.








