Received 2 July 2015; accepted 22 August 2015; published 26 August 2015

ABSTRACT

A proper edge colouring f of a graph G is called acyclic if there are no bichromatic cycles in the graph. The acyclic edge chromatic number or acyclic chromatic index, denoted by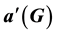, is the minimum number of colours in an acyclic edge colouring of G. In this paper, we discuss the acyclic edge colouring of middle, central, total and line graphs of prime related star graph families. Also exact values of acyclic chromatic indices of such graphs are derived and some of their structural properties are discussed.

Keywords:

Acyclic Edge Colouring, Acyclic Chromatic Index, Middle Graph, Central Graph, Total Graph, Line Graph

1. Introduction

All graphs considered in this paper are finite, undirected and simple. The concept of acyclic colouring of a graph was introduced by B. Grunbaum [1] . A proper edge colouring of a graph G = (V, E) with vertex set V and edge set E, is a map f: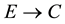, where C is the set of colours with f(x) ≠ f(y) for any adjacent edges x, y of E. The minimum number of colours needed to properly colour the edges of G, is called the chromatic index of G and is denoted by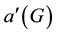. A proper edge colouring f is called acyclic if there are no bichromatic cycles in the graph. The acyclic edge chromatic number or acyclic chromatic index, denoted by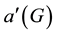, is the minimum number of colours in an acyclicedge colouring of G.

Consider the set X of lines of a graph G with at least one line as a family of 2-point subsets of V(G). The line graph [2] of graph G, denoted by L(G), is the intersection graph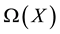. Thus the points of L(G) are the lines of G, with two points of L(G) which are adjacent whenever the corresponding lines of G are.

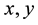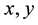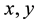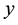Let G be a graph with vertex set V(G) and edge set E(G). The middle graph [3] of G, denoted by M(G) is a graph with vertex set in which two vertices are adjacent in M(G) if one of following holds. (i) are in E (G) and are adjacent in G; (ii) is in V(G), is in E(G), and are incident in G.

Let G be a finite simple graph. The central graph [4] of a graph G, denoted by C(G) is obtained by subdividing each edge of G exactly once and joining all the non-adjacent vertices of G.

Let G be a graph with vertex set V(G) and edge set E(G). The total graph [2] [3] of G, denoted by T(G) is a graph with vertex set in which two vertices are adjacent in T(G) if one of the following holds. (i) 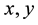are in V(G) and 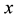is adjacent to in G; (ii) are in E(G) and are adjacent in G; (iii) is in, is in E(G), and are incident in G.

Determining is a hard problem both from a theoretical and from an algorithmic point of view. Even for the simple and highly-structured class of complete graphs, the value of is still not determined exactly. It has also been shown by Alon and Zaks [5] that determining whether is NP-complete for an arbitrary graph G.

Alon, Sudakov and Zaks [6] proved that for almost all D-regular graphs. This result was improved by Nesetril and Wormald [7] who showed that for a random D-regular graph.

In view of the discussion relating acyclic edge colouring to perfect 1-factorization conjecture, it may be inferred that finding the exact values of for every n seems hard. However, Alon et al. [8] designed an algorithm that can acyclically edge colour. Through this work, they constructively showed that.

2. Acyclic Edge Colouring of Line Graph of a Star Graph

Theorem

The acyclic chromatic index, for prime

Proof

As the line graph of the star graph is isomorphic to the complete graph and by Alon et al. [8] ,.

3. Acyclic Edge Colouring of Middle Graph of a Star Graph

Theorem

For the star graph the acyclic chromatic index, , where is prime,.

Proof

Let the edge set and vertex set with as the root vertex. By definition, in the middle graph, the vertex set is. From the definition of middle graph the vertices induce a clique of order, say in. See Figure 1, given below. Now assign a proper colouring to the vertices of as follows. Consider the colour class. Assign the colour i to the edges as follows.

One can easily check that it is an acyclic edge colouring of and hence Also

. Hence.

Example 3.1.

4. Acyclic Edge Colouring of Central Graph of a Star Graph

4.1. The Structural Properties Central Graph of Star Graph

Ÿ The maximum degree in the graph is

Ÿ The minimum degree in the graph is

Ÿ Number of edges in the graph,

Ÿ The number of vertices in,

4.2. Theorem

For the graph the acyclic chromatic index, for prime

Proof

Let with as the root vertex. In central graph, by the definition each edge for of is subdivided by the vertex in. i.e. . Now the vertices induce a clique of order, say in. See Figure 2.

Now assign a proper colouring to the vertices of as follows. Consider the colour class. Assign the colour i to the edges as follows.

One can easily check that it is an acyclic edge colouring of and hence. Also

. Hence.

Example 4.2.

5. Acyclic Edge Colouring of Total Graph of a Star Graph

5.1. Structural Properties of

Ÿ The maximum degree in the graph is.

Ÿ The minimum degree in the graph is.

Ÿ The number of edges in the graph, is.

Ÿ The number of vertices in, is.

5.2. Theorem

For any star graph the acyclic chromatic index, , for prime.

Proof

Let and with as the root vertex. By definition, in the total graph, the vertex set is

. Now the vertices induce a

clique of order, say in. See Figure 3.

Now assign a proper colouring to the vertices of as follows. Consider the colour class , say. Assign the colour i to the edges as follows.

These colouring takes colours using and the remaining edges are assigned to the colours.

One can easily check that it is an acyclic edge colouring of and hence Also

since, minimum colours are required for its proper edge colouring.

Hence.

Example 5.2.

Cite this paper

P.Shanasbabu,A. V.Chithra, (2015) A Note on Acyclic Edge Colouring of Star Graph Families. American Journal of Computational Mathematics,05,253-257. doi: 10.4236/ajcm.2015.53022

References