American Journal of Computational Mathematics
Vol.04 No.05(2014), Article ID:51292,7 pages
10.4236/ajcm.2014.45035
Statistical Modelling of Soybean Crop Yield in Regions of Central India through Mathematical and Computational Approach
Sarvraj Singh1, Dilpreet Tuteja1, Param Tripathi1, Chirag Basavaraj2
1Jaypee University of Engineering & Technology, Guna, India
2R.V. College of Engineering, Bangalore, India
Email: sarvraj.5@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 August 2014; revised 15 September 2014; accepted 1 October 2014
ABSTRACT
In this paper, we have discussed a number of fitting methods to predict crop yield of soybean depending on the nature of environment and a comparison is done between them on the basis of available data set. Later we have suggested a suitable method for the prediction of the crop yield on the basis of residual (error) terms. Statistical analysis is also used for getting the relationships between different components (variables) of available data set. At last, we have discussed about Chaos that can distort the whole mathematical analysis and a computational approach.
Keywords:
Climate Change, Prediction, Chaos, Uncertainty

1. Introduction
Climate describes the ensemble sum of typical conditions of temperature, relative humidity, cloudiness, precipitation, wind speed and direction and innumerable other meteorological factors that prevail regionally for extended periods [1] . Weather of a demographic region is defined by the hourly description of the climatic conditions experienced by the inhabitants of that region. Here we discuss the soybean yield as a function of these environmental parameters.
Many different approaches are used for constraining climate based crop yield predictions based on observations of past empirical change in the yield [2] . Here we setup distinct models based on the environmental model parameters; significant correlations are calculated based on the inferred outputs. Meteorologists say that if only they could design an accurate mathematical model of the atmosphere with all its complexities, they could forecast the weather with real precision. But this is an idle boast, immune to any evaluation, for any inadequate weather forecast would obviously be blamed on imperfections in the model. Catering to the often glitches in the models prepared the fidelity of the dynamics governing the respective models can be doubted. With the introduction of computer simulations the weather predictions can be done in just a few minutes. We make use of such a technique to generalize the crop yield, and make prediction on the basis of the environmental factors like wind speed, wind direction, temperature and humidity. These factors are trivial when considering crop yield however, makes a difference as suggested by the models ahead.
Since the sensors of the parameters mentioned above are respect to one region in Central India, so we consider the crop that this region has lavishly produced, soybean. Soybean is one of the important crops of the world [3] . In India the production of soybean is currently restricted to mainly Madhya Pradesh, Uttar Pradesh, Maharashtra and Gujarat. Himachal Pradesh, Punjab and Delhi are other states with some marginal produce. According to 2010 estimates of soybean production India produces 4.4% of the total production; central India is the largest contributor of soybean yield. This brings us to concentrate more over this region for our fitting models.
Soybean is a crop that grows in warm and moist climate. An optimum yield requires a temperature ranging between 26.5˚C to 30˚C. For rapid germination and vigorous seedling growth soil temperatures of 15.5˚C or above are most suitable. A lower temperature delays flowering. Although, moisture enhances the yield of the crop but excess of moisture can make it prone to foliar diseases like frogeye leafs spot and septoria brown spot. Therefore, an optimum amount of humidity is required for the crop.
Wind direction and velocity also have a significant influence on crop growth [4] . While it has a few benefits, gusty winds blowing in one direction can harm the crop. Beneficial impacts include increasing the supply of carbon dioxide by increasing turbulence in the atmosphere. It also alters the balance of hormones. Strong winds in a region may uproot the crop or be an inevitable carrier of dispersive seeds that may hamper the yield. Table 1 elucidates the conditions prevalent in Central India, state of Madhya Pradesh that monitor the soybean growth.
As far as the prediction of the yield on a larger perspective is considered, the simulations carried out by supercomputers are based on curve fitting methods. Curve fitting is the process of constructing a curve that has the best fit to a series of data points, possibly subject to constraints. Curve fitting involves interpolation [5] , where an exact fit to the data is required in which a “smooth” function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference which includes the uncertainty present due to the random errors in the observed data. Fitted curves can be used as approximate data visualization for a model to which it is applied and to summarize the relationships among two or more variables.
Table 1. Varying environmental parameters dependent for yield of soybean in Central India.
Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a greater degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data. In order to fit a polynomial up to three degree which exactly fits four constraints, each constraint can be a point, angle, or curvature (which is the reciprocal of the radius of an osculating circle). Angle and curvature constraints are most often added to the ends of a curve, and in such cases are called end conditions. Identical end conditions are frequently used to ensure a smooth transition between polynomial curves contained within a single spline. If we have more than n + 1 constraints (n is the degree of the polynomial), we can still run the polynomial curve through those constraints. An exact fit to all constraints is not certain (but it might happen, for example, in the case of a first degree polynomial exactly fitting three collinear points). In general, however, some method is then needed to evaluate each approximation. The least squares method is one way to compare the deviations.
Low-order polynomials tend to be smooth and high order polynomial curves tend to be lumpy. To define this more precisely, the maximum number of inflection points possible in a polynomial curve is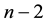 , where n is the order of the polynomial equation. An inflection point is a location on the curve where it switches from a positive radius to negative. It is only possible that high order polynomials will be lumpy; they could also be smooth, but there is no guarantee of this, unlike with low order polynomial curves. A fifteenth degree polynomial could have, at most, thirteen inflection points, but could also have twelve, eleven, or any number down to zero.
, where n is the order of the polynomial equation. An inflection point is a location on the curve where it switches from a positive radius to negative. It is only possible that high order polynomials will be lumpy; they could also be smooth, but there is no guarantee of this, unlike with low order polynomial curves. A fifteenth degree polynomial could have, at most, thirteen inflection points, but could also have twelve, eleven, or any number down to zero.
2. Fitting a Polynomial Function
When a given set of data does not appear to satisfy a linear equation, we can try a suitable polynomial as a regression curve to fit data. The least squares technique can be readily used to fit the data to a polynomial.
Consider a polynomial of degree 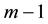
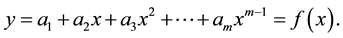 (1)
(1)
If the data contains n sets of x and y values, then the sum of squares of the errors is given by
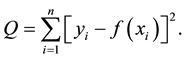 (2)
(2)
Since 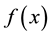 is a polynomial and contains coefficients a1, a2, a3 etc. we have to estimate all m coefficients. As before, we have the following m equations that can be solved for these coefficients.
is a polynomial and contains coefficients a1, a2, a3 etc. we have to estimate all m coefficients. As before, we have the following m equations that can be solved for these coefficients.
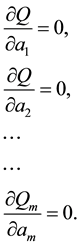
Consider a general term,
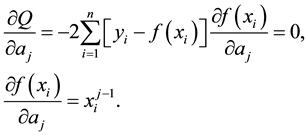
Thus we have
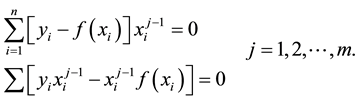
Substituting for 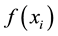
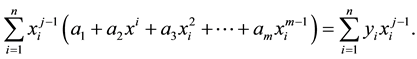
These are m equations 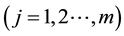 and each summation is for
and each summation is for  to n.
to n.
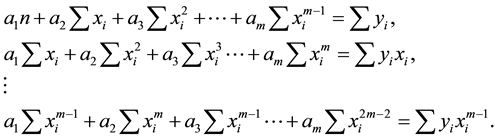
The set of m equations can be represented in a matrix notation as follows:
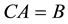
where
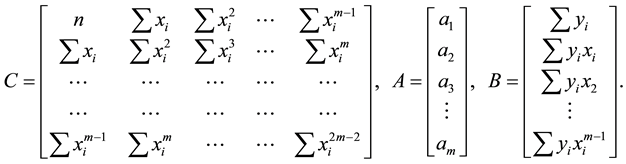
The element of matrix C is
The first model which we fit the yearly soybean yield is the linear model described by

where a0 being a constant term, w is the wind direction in degree, x being temperature parameter in degree Celsius, “y” the percentage humidity, “z” is the speed of wind in km/hr.
The error in the generalisation

And squaring the error term for Minimum Squared Error

Differentiating with respect to various factors, similar to equation for the weighted coefficients for the parameters that determine the yield, given by
The yield that is 
Solving the equations to get the values of the weighted coefficients
Generalizing the model the yield can be predicted by
where the w, x, y, z are the parameters discussed above.
The second model which we fit the yearly soybean yield is the linear model described by

where a0 being a constant term, w is the wind direction in degrees, x being temperature parameter in degree Celsius, “y” the percentage humidity, “z” is the speed of wind in km/hr.
The error in the generalisation

And squaring the error term for Minimum Squared Error

Differentiating with respect to various factors, similar to equation for the weighted coefficients for the parameters that determine the yield, given by
The yield that is 
Solving the equations to get the values of the weighted coefficients
Generalizing the model the yield can be predicted by
where the w, x, y, z are the parameters discussed above.
The third model which we fit the yearly soybean yield is the linear model described by

where a0 being a constant term, w is the wind direction in degrees, x being temperature parameter in degree Celsius, “y” the percentage humidity, “z” is the speed of wind in km/hr.
The error in the generalisation

And squaring the error term for Minimum Squared Error

Differentiating with respect to various factors, similar to equation for the weighted coefficients for the parameters that determine the yield, given by
The yield that is 
Solving the equations to get the values of the weighted coefficients
Generalizing the model the yield can be predicted by
where the w, x, y, z are the parameters discussed above.
3. Chaos
Chaos is associated with complex and unpredictable behavior of phenomena over time [7] . Such behavior can arise in deterministic dynamical systems. These processes are intriguing in that the realizations corresponding to different, although extremely close, initial conditions typically diverge. The practical implication of this phenomenon is that, despite the underlying determinism, we cannot predict, with any reasonable precision, the values of the process for large time values; even the slightest error in specifying the initial condition eventually ruins our attempt. The chaos in terms of correlation coefficient within various environmental factors (say n) is given by
4. Conclusion
Table 2 describes the possible correlation permutation and Table 3 elucidates the variability of the yield amongst the different models under scrutiny. The results suggest, about the dependence of the yield on the environmental factors more under the variable weighted powers rather than being in linearly or quadratic fashion. Figure 1 shows the proper harvesting time of the season for maximising the yield of soybean. The data are indeed direct acceptance of the model variable power model as the data match with the conventional values of
Figure 1. Statistical yield suggested by the third model for the yield of soybean in Central India.
Table 2. Correlation permutations amongst various environmental factors.
Table 3. Correct prediction percentage amongst the three models under consideration.
the 2012 estimate, thereby proving the legitimacy of the accuracy of the computational calculation of yield using hidden environmental parameters.
References
- Schwartz, M.D. (1995) Detecting Structural Climate Change: An Air Mass-Based Approach in the North Central United States, 1958-1992. Annals of the Association of American Geographers, 85, 553-568. http://dx.doi.org/10.1111/j.1467-8306.1995.tb01812.x
- Fahd, T. (1996) Botany and Agriculture. In: Morelon, R. and Rashed, R., Eds., Encyclopedia of the History of Arabic Science, Routledge, London, 815.
- Saxena, M.C. and Pandeny, R.K. (1972) Characteristics and Performance of Some Promising Varieties of Soybean. Indian Journal of Agricultural Sciences, 41.
- Bansil, P.C. (1984) A Strategy for Self Sufficiency in Vegetable Oils. Quarterly Economic and Agricultural Report, 27.
- Ahn, S.-J. (2008) Geometric Fitting of Parametric Curves and Surfaces. Journal of Information Processing Systems, 4.
- (2013) All India State Wise Production and Yield of Soybean, First Estimate, Soybean Production Association of India.
- Devaney, R.L. (2003) An Introduction to Chaotic Dynamical Systems. 2nd Edition, Westview Press, Boulder.















