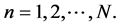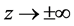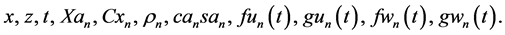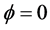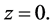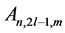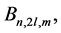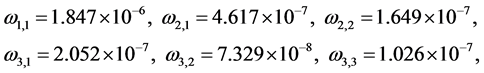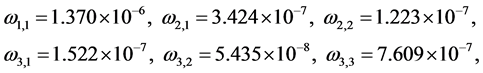American Journal of Computational Mathematics
Vol.04 No.04(2014), Article ID:49366,14 pages
10.4236/ajcm.2014.44025
Deterministic Chaos of N Stochastic Waves in Two Dimensions
Victor A. Miroshnikov
Department of Mathematics, College of Mount Saint Vincent, New York, USA
Email: victor.miroshnikov@mountsaintvincent.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 June 2014; revised 23 July 2014; accepted 2 August 2014
ABSTRACT
Kinematic exponential Fourier (KEF) structures, dynamic exponential (DEF) Fourier structures, and KEF-DEF structures with time-dependent structural coefficients are developed to examine kinematic and dynamic problems for a deterministic chaos of N stochastic waves in the two-dimen- sional theory of the Newtonian flows with harmonic velocity. The Dirichlet problems are formulated for kinematic and dynamics systems of the vorticity, continuity, Helmholtz, Lamb-Helmholtz, and Bernoulli equations in the upper and lower domains for stochastic waves vanishing at infinity. Development of the novel method of solving partial differential equations through decomposition in invariant structures is resumed by using experimental and theoretical computation in Maple™. This computational method generalizes the analytical methods of separation of variables and undetermined coefficients. Exact solutions for the deterministic chaos of upper and lower cumulative flows are revealed by experimental computing, proved by theoretical computing, and justified by the system of Navier-Stokes PDEs. Various scenarios of a developed wave chaos are modeled by 3N parameters and 2N boundary functions, which exhibit stochastic behavior.
Keywords:
Stochastic Waves, Invariant Structures, Experimental Computation, Theoretical Computation

1. Introduction
The two-dimensional (2d) Navier-Stokes system of partial differential equations (PDEs) for a Newtonian fluid with a constant density  and a constant kinematic viscosity
and a constant kinematic viscosity 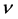 in a gravity field
in a gravity field 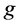 is
is
 (1)
(1)
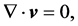 (2)
(2)
where 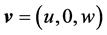 is a vector field of the flow velocity,
is a vector field of the flow velocity,  is a vector field of the gravitational acceleration,
is a vector field of the gravitational acceleration,  is a scalar field of the total pressure,
is a scalar field of the total pressure, 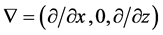 and
and 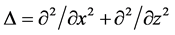 are the gradient and the Laplacian in the 2d Cartesian coordinate system
are the gradient and the Laplacian in the 2d Cartesian coordinate system 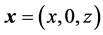 of the three-dimensional (3d) space with unit vectors
of the three-dimensional (3d) space with unit vectors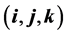 , respectively, and t is time.
, respectively, and t is time.
By a flow vorticity 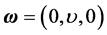 of the velocity field
of the velocity field
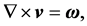 (3)
(3)
Equation (1) may be written into the Lamb-Pozrikidis form [1] [2]
 (4)
(4)
which sets a dynamic balance of inertial, potential, vortical, and viscous forces, respectively.
Using a dynamic pressure per unit mass [3]
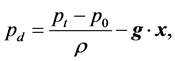 (5)
(5)
where 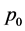
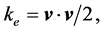
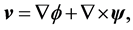
and the vortex force
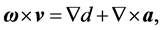
Equation (4) is reduced to the Lamb-Helmholtz PDE [5]

for a scalar Bernoulli potential and a vector Helmholtz potential, respectively,

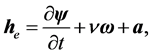
where 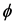
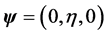
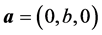
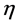
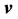

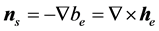
shows that a virtual force 
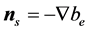
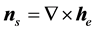
The exponential Fourier eigenfunctions obtained by the classical method of separation of variables of the 2d Laplace equation in [1] and [4] were primarily used for a linear part of the kinematic problem for free-surface waves of the theory of the ideal fluid with 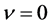
To examine linear and nonlinear parts of kinematic and dynamic problems for 2d stochastic waves in the theory of Newtonian flows with harmonic velocity, the KEF structures, the DEF structures, and the KEF-DEF structures with time-dependent structural coefficients are developed in the current paper. The structure of this paper is as follows. The KEF structures are used to compute theoretical solutions of the kinematic problems for the velocity components and the dual potentials of the velocity field in Section 2. The KEF and KEF-DEF structures are employed for theoretical computation of the dynamic problems for the Helmholtz and Bernoulli potentials, the kinetic energy, and the total pressure in Section 3. Verification of the experimental and theoretical solutions is also provided in Section 3. Various scenarios of a developed wave chaos are treated in Section 4. A summary of main results is given in Section 5.
2. Kinematic Problems for Internal Waves
The following solutions and admissible boundary conditions for the kinematic problems of Section 2 in the KEF and DEF structures with time-dependent coefficients were primarily computed via experimental programming techniques, which use lists of equations and expressions of Maple™ in the virtual environment of a global variable Eqs with 25 procedures of 600 code lines in total.
2.1. Formulation of Theoretical Kinematic Problems for the Velocity Field
Theoretical kinematic problems for harmonic velocity components 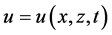

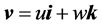
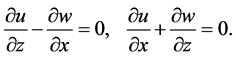
To consider a deterministic chaos of N internal, stochastic waves, the cumulative flow is decomposed into a superposition of local flows
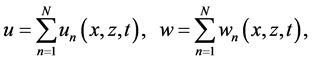
such that the local vorticity and continuity equations are
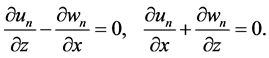
where
An upper cumulative flow is specified by the Dirichlet condition in the KF structure on a lower boundary 
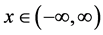
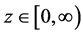
Figure 1. Configuration of upper and lower domains for stochastic waves.
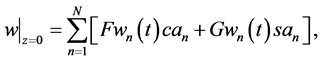
and a vanishing condition as
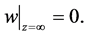
A lower cumulative flow is identified by the Dirichlet condition on an upper boundary 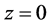
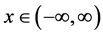

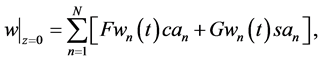
and a vanishing condition as
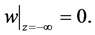
Thus, an effect of surface waves on the internal waves is described by the Dirichlet conditions (15) and (17). Here, a structural notation
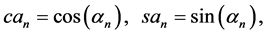
is used for kinematic structural functions 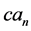
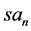
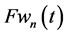
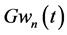

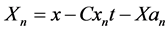
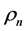
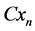
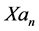


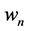
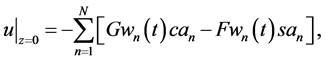

Similarly to w, u vanishes as
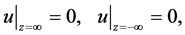
for the upper and lower cumulative flows, respectively.
2.2. Theoretical Solutions for the Velocity Field
Theoretical solutions of kinematic problems (12)-(18) are constructed in the KEF structure 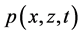
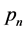
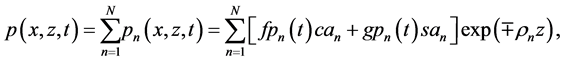
where signs “−” and “+” of the exponential term refer to the upper and lower flows, respectively, first letters f and g of structural coefficients 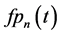

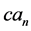
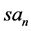
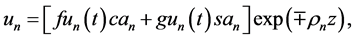

It may be shown that spatial derivatives of 
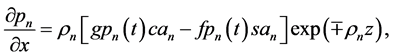
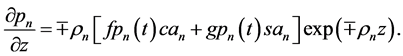
Application of (26) (27) to (24) (25), substitution in (14), collection of the structural functions, and vanishing their coefficients reduce two vorticity and continuity PDEs to the following system of four vorticity and continuity algebraic equations (AEs) with respect to 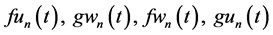
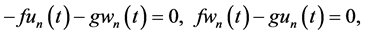
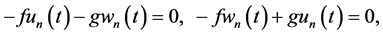
the lower flows
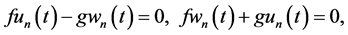
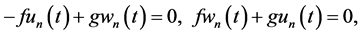
and all
Solving AEs (28) and (30) yields for the upper and lower flows, respectively,
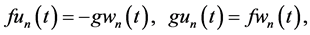

Substitution of solutions (32) in (29) and (33) in (31) reduces them to identities, showing that vorticity and continuity AEs (28)-(31) are compatible. Finally, substitution of (32) (33) in the KEF structures (24) (25) and solving the Dirichlet boundary conditions (15) and (17) with respect to 
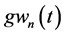

while vanishing boundary conditions (16) and (18) are obviously satisfied.
2.3. The DEF Structure and Theoretical Jacobian Determinants of the Velocity Field
Define two KEF structures 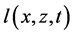
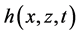
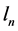
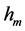
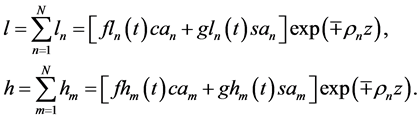
Following [5] , define structural functions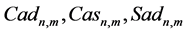
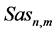
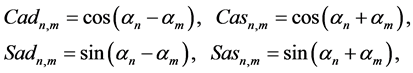
where capital letters C and S stand for dynamic structural functions cosine and sine, letter a for arguments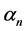
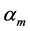
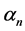
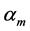
Computation of a general term 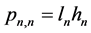

A general term 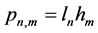
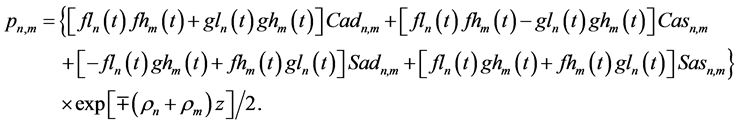
By triangular summation, 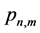
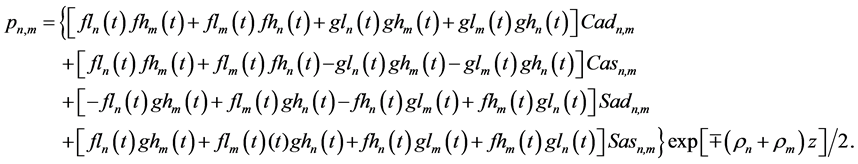
By (37) and (39), summation formula for the product of the KEF structures may be written as the DEF structure with time-dependent structural coefficients
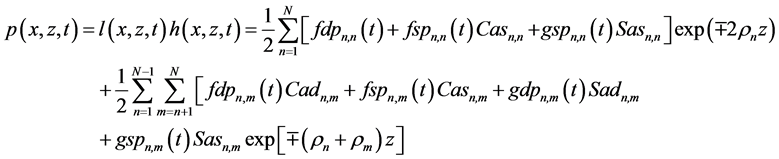
with the following structural coefficients:

where first two letters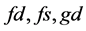

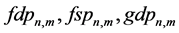
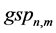

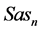
Computation of local JDs for the velocity components of the upper and lower flow, respectively, yields
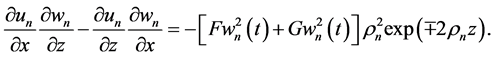
Thus, velocity components 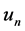
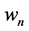
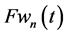
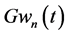
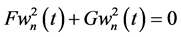
Computation of a global JD by using (40) (41) for velocity components of the upper and lower cumulative flows (34) with slant internal waves gives
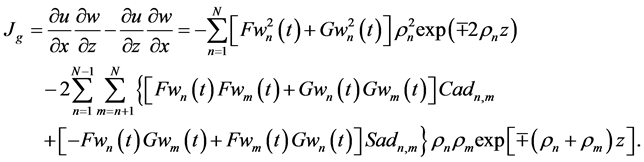
So, 

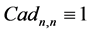
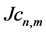

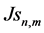
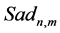
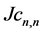
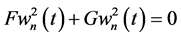
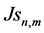
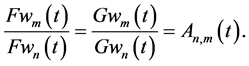
Global JD (43) then becomes
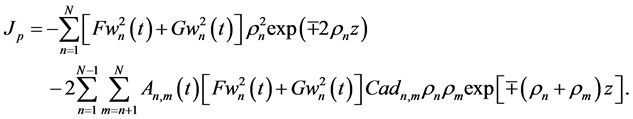
Thus, the global JD does not vanish for parallel waves with non-vanishing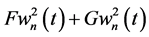
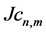
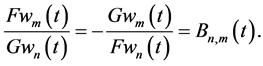
In this case, global JD (43) is reduced to
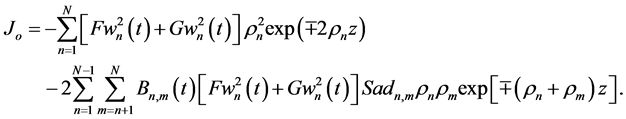
So, the global JD does not vanish also for orthogonal waves with non-vanishing 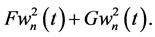
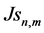
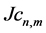
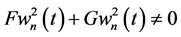
2.4. Theoretical Solutions for the Kinematic Potentials in the KEF Structures
Theoretical kinematic problems for cumulative pseudovector potential 
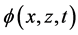
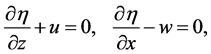
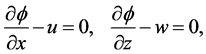
since the potential-vortical duality the velocity field admits two presentations: 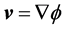
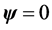
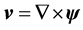

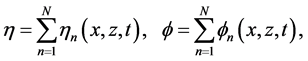
such that the local Helmholtz PDEs are
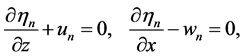
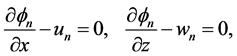
where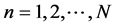
Construct general terms of the kinematic potentials of the local flows in the KEF structure with time-depen- dent coefficients
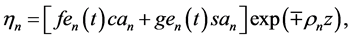

Application of (26) (27) to (53) (54), substitution in the Helmholtz PDEs (51) (52), collection of the structural functions, and vanishing their coefficients reduce four Helmholtz PDEs to the following system of eight Helmholtz AEs for the upper flows
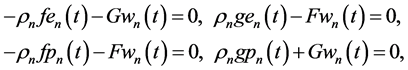
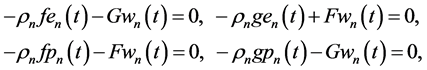
the lower flows


and all
Solving AEs (55) and (57) with respect to time-dependent structural coefficients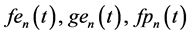
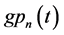
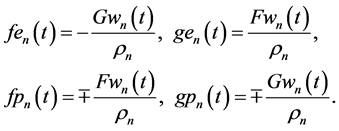
Substitution of solutions (59) in AEs (56) and (58) reduces them to identities. Finally, substitution of structural coefficients (59) in the KEF structures (53) (54) and superpositions (50) yields the cumulative kinematic potentials in the KEF structures for the upper and lower cumulative flows, respectively,
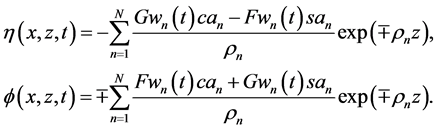
The theoretical solutions in the KEF and DEF structures for the kinematic problems of Section 2 were computed utilizing theoretical programming methods with symbolic general terms in the virtual environment of a global variable Eqt with 21 procedures of 522 Maple code lines in total. The theoretical formulas for velocity components (34), the products of the KEF structures (40) (41), and the kinematic potentials (60) of the upper and lower cumulative flows were justified by the correspondent experimental solutions for N = 1, 3, 10.
3. Dynamic Problems for Internal Waves
The following solutions for the dynamic problems of Section 3 in the KEF, DEF, and KEF-DEF structures were primarily computed by experimental programming with lists of equations and expressions in the virtual environment of the global variable Eqs with 18 procedures of 470 code lines in total.
3.1. Theoretical Solutions for the Dynamic Potentials in the KEF Structures
Theoretical dynamic problems in the KF structures for the Helmholtz and Bernoulli potentials of the cumulative flows are set by the Lamb-Helmholtz PDEs (8)-(10) in the vortical presentation with
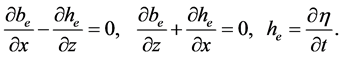
Equations (61) are complemented by the local Lamb-Helmholtz PDEs
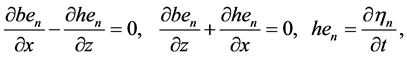
since the cumulative dynamic potentials are again decomposed into the local dynamic potentials
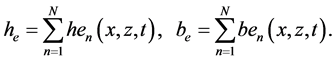
Construct a general term of the Bernoulli potential of the local flows in the KEF structure with time-depen- dent coefficients
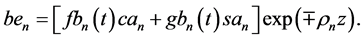
Computation of the temporal derivative of
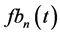
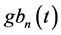
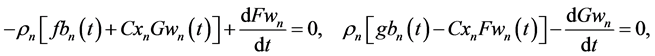
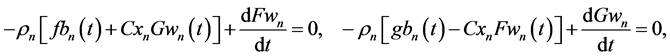
and the lower flows
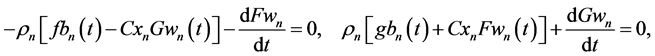
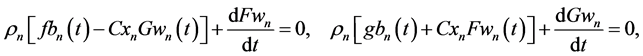
and all variables, parameters, and functions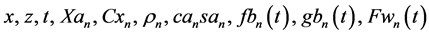
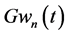
Solving AEs (65) and (67) for structural coefficients 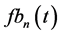
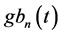
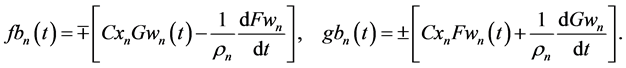
Substitution of solutions (69) in AEs (66) and (68) reduces them to identities. Eventually, substitution of structural coefficients (69) in the KEF structure (64) and superpositions (63) returns the cumulative dynamic potentials in the KEF structures for the upper and lower cumulative flows, respectively,
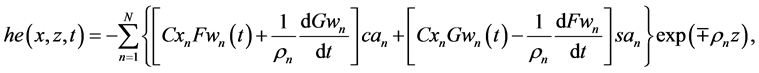
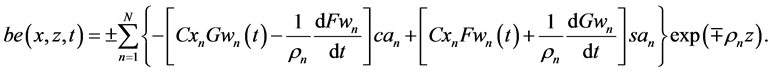
3.2. Theoretical Solutions for the Total Pressure in the KEF-DEF Structures
Theoretical dynamic problems in the KEF-DEF structures for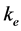
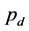
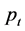

the Bernoulli Equation (9) with
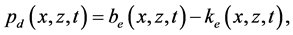
and the hydrostatic Equation (5)
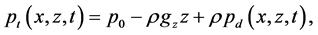
where 
Computation of 
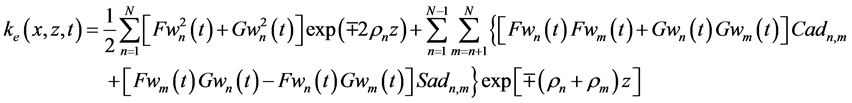
for the upper and lower cumulative flows, respectively. Substitution of (71), (75), and (73) in (74) yields
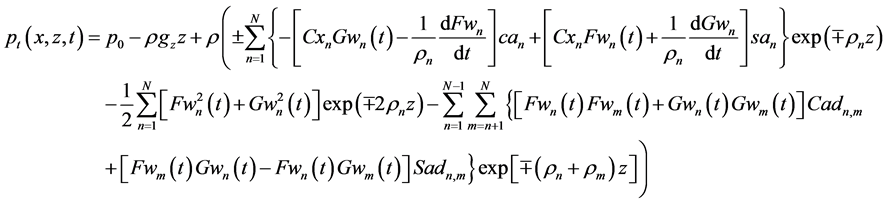
for the upper and lower cumulative flows, respectively. So, the kinetic energy is obtained in the DEF structures, the dynamic pressure is expressed in the KEF-DEF structures, and the total pressure is computed in the KEF-DEF and polynomial structures.
3.3. Harmonic Relationships between the Kinematic and Dynamic Variables
Similar to the invariant trigonometric, hyperbolic, and elliptic structures [8] , there are two pairs of independent KEF structures: generating structures with general terms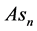
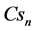
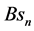
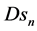

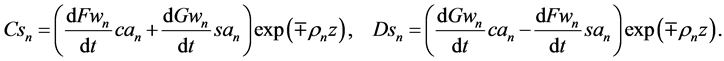
Expressing velocity components (34), kinematic potentials (60), and dynamic potentials (70) (71) through the generating and complementary structures (77) (78) and solving for 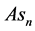
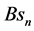

Taking derivatives of (34) and (60) with respect to x, z and solving for 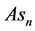
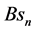
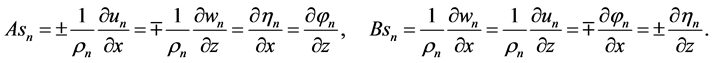
In fluid dynamics, relationships (79) (80) mean that a harmonic flow, which is non-uniform in 

Computing velocity components (34) and dynamic potentials (70) (71) through the generating and complementary structures (77) (78), taking temporal and spatial derivatives, and solving for 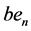

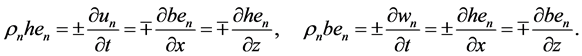
Differential relationships (81) mean that spatial derivatives of the dynamic potentials generate temporal rates of a harmonic flow.
By the following substitutions:
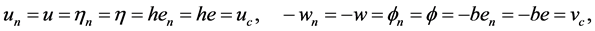
both local and global vorticity and continuity Equations (12) and (14), Helmholtz Equations (48)-(49) and (51)- (52), and Lamb-Helmholtz Equations (61) and (62), respectively, are reduced to the Cauchy-Riemann equations
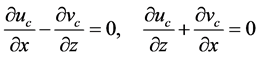
for conjugate functions 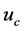
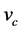

and vanishing Laplacians,
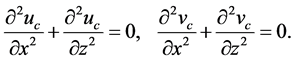
Thus, 
3.4. Theoretical Verification by the System of Navier-Stokes PDEs
The system of the Navier-Stokes PDEs (1)-(2) in the scalar notation becomes
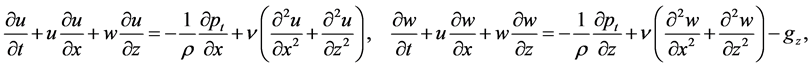

Computation of spatial derivatives of (34) by (26)-(27) reduces (87) to identity both for the upper and lower cumulative flows.
Temporal derivatives of 
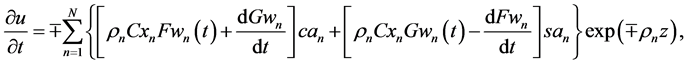
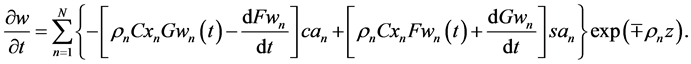
The directional derivatives of (86) computed by (40)-(41) in the DEF structures for the upper and lower cumulative flows, respectively, become
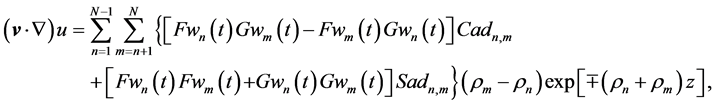
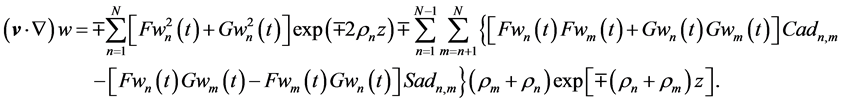
By using (26)-(27), components of the gradient of (76) may be written in the KEF-DEF structures for the upper and lower cumulative flows, respectively, as
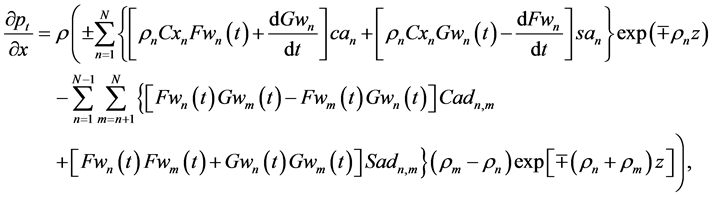
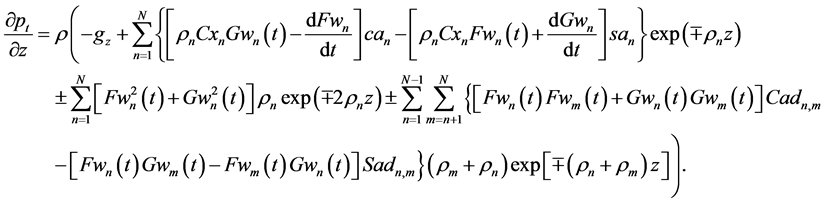
Substitution of Equations (88)-(93) and (85) for u and w in (86) reduces then to identities. Thus, Equations (34) and (76) constitute exact solutions in the KEF, DEF, and KEF-DEF structures with time-dependent structural coefficients for deterministic chaos of N stochastic waves both in the upper and lower domains.
The theoretical solutions in the KEF, DEF, and KEF-DEF structures for the dynamic problems of Section 3 were computed by theoretical programming methods with symbolic general terms in the virtual environment of the global variable Eqt with 14 procedures of 410 code lines in total. The theoretical solutions for Helmholtz and Bernoulli potentials (70)-(71), total pressure (76), temporal derivatives (88)-(89), directional derivatives (90)- (91), and pressure gradient (92)-(93) of the upper and lower cumulative flows were justified by the correspondent experimental solutions for N = 1, 3, 10.
All kinematic solutions of Section 2 and dynamic solutions of Section 3 with time-dependent structural coefficients are reduced to the correspondent solutions of [5] when 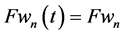
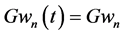
4. Chaotic Scenarios
Boundary functions 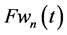
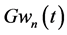
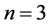
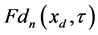
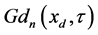
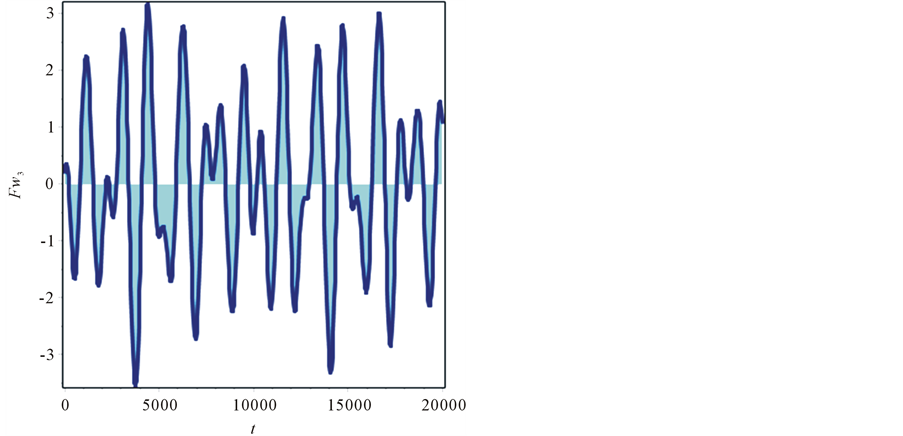
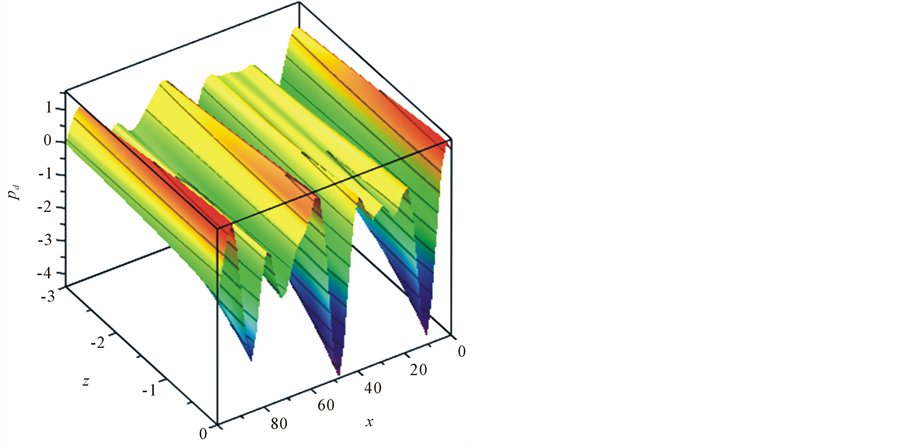
Figure 2. Stochastic boundary functions.
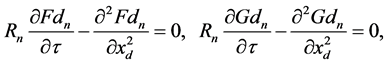
where 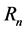
In agreement with [7] , 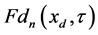
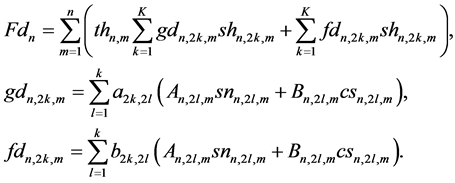

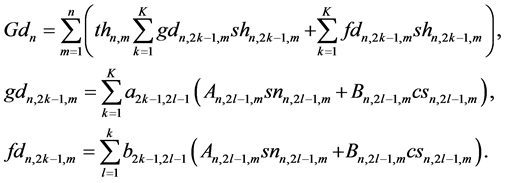
Here, a structural notation
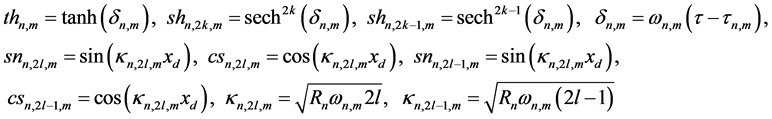
is used for structural functions of temporal and spatial modes, where 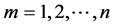

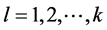
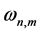
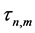

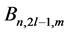

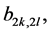
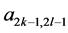
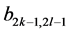
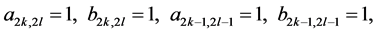
and recurrent relations
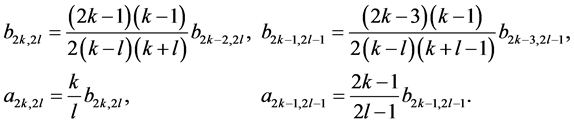
In Figure 2, stochastic boundary functions
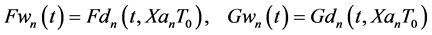
were evaluated for
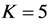
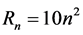
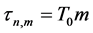
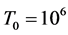


and spatial amplitudes

which insure convergence of the spatial modes. Frequencies of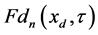
and frequencies of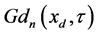
were computed by iterations from tolerance equations
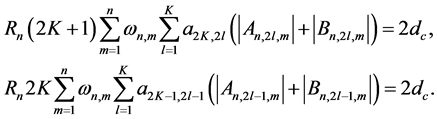
These equations guarantee that absolute values of remainders of the structural approximations of (94)
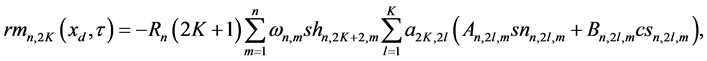
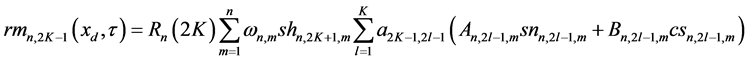
do not exceed 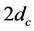


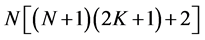
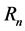
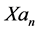
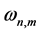
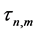
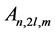

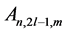
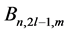
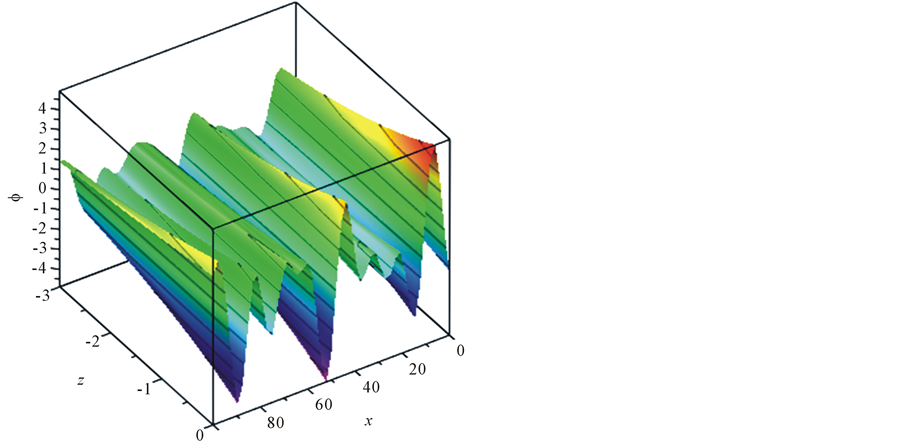
The KEF structures and KEF-DEF structures are visualized in Figure 3 by instantaneous 3d surface plots with isocurves at 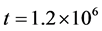

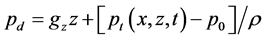

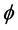
Figure 3. Scalar potential (left) and dynamic pressure (right) of the lower cumulative flow.
waves. The temporal structure of 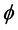
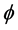
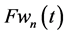
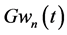
5. Conclusions
The computational method of solving PDEs by decomposition in invariant structures, which continues the analytical methods of separation of variables and undetermined coefficients, is generalized in the current paper at the KEF, DEF, and KEF-DEF structures with time-dependent coefficients. This computational method is implemented in the kinematic and dynamic problems for internal waves by 43 procedures with 1070 code lines of the experimental computing in total and 35 procedures with 932 code lines of the theoretical computing in total. These structures with time-dependent structural coefficients are invariant with respect to various differential and algebraic operations.
For internal waves vanishing at infinity in the upper and lower domains, the Dirichlet problems are formulated for the kinematic and dynamic systems of the vorticity, continuity, Helmholtz, Lamb-Helmholtz, and Bernoulli equations. The exact solutions of the Navier-Stokes PDEs for the deterministic chaos of N stochastic waves are revealed experimentally, proved theoretically, and justified by the system of Navier-Stokes PDEs in the class of flows with the harmonic velocity field. The kinematic and dynamic solutions for stochastic waves coincide with the correspondent solutions for conservative waves [5] when stochastic boundary functions are reduced to constants.
Independence of both propagating and interacting internal waves is shown by computation of the Jacobian determinants in the DEF structures. Conditions for existence of parallel and orthogonal waves with time-de- pendent amplitudes are obtained through the Jacobian determinants, as well. The harmonic relationships between six pairs of the harmonic, fluid-dynamic variables, their temporal derivatives, and their spatial derivatives with respect to x and z are derived both for the upper and lower flows.
The stochastic boundary functions are constructed from the stochastic solutions of the one-dimensional Navier-Stokes equation [7] with hyperbolic temporal modes and trigonometric spatial modes in the HETO, HETE, HOTO, and HOTE structures. Various scenarios of a developed wave chaos are modeled by 3N parameters for internal waves and 2N stochastic boundary functions, which depend on 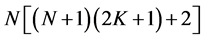
Acknowledgements
The author thanks S. P. Bhavaraju for the stimulating discussion at the 2013 SIAM Annual Meeting. Support of the College of Mount Saint Vincent and CAAM is gratefully acknowledged.
References
- Lamb, S.H. (1945) Hydrodynamics. 6th Edition, Dover Publications, New York.
- Pozrikidis, C. (2011) Introduction to Theoretical and Computational Fluid Dynamics. 2nd Edition, Oxford University Press, Oxford.
- Miroshnikov, V.A. (2005) The Boussinesq-Rayleigh Series for Two-Dimensional Flows away from Boundaries. Applied Mathematics Research Express, 2005, 183-227. http://dx.doi.org/10.1155/AMRX.2005.183
- Korn, G.A. and Korn, T.A. (2000) Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. 2nd Revised Edition, Dover Publications, New York.
- Miroshnikov, V.A. (2014) Nonlinear Interaction of N Conservative Waves in Two Dimensions. American Journal of Computational Mathematics, 4, 127-142. http://dx.doi.org/10.4236/ajcm.2014.43012
- Kochin, N.E., Kibel, I.A. and Roze, N.V. (1964) Theoretical Hydromechanics. John Wiley & Sons Ltd., Chichester.
- Miroshnikov, V.A. (2009) Spatiotemporal Cascades of Exposed and Hidden Perturbations of the Couette Flow. Advances and Applications in Fluid Dynamics, 6, 141-165.
- Miroshnikov, V.A. (2012) Dual Perturbations of the Poiseuille-Hagen Flow in Invariant Elliptic Structures. Advances and Applications in Fluid Dynamics, 11, 1-58.