American Journal of Computational Mathematics
Vol.4 No.2(2014), Article ID:43980,14 pages
DOI:10.4236/ajcm.2014.42007
High Accurate Fourth-Order Finite Difference Solutions of the Three Dimensional Poisson’s Equation in Cylindrical Coordinate
Alemayehu Shiferaw, Ramesh Chand Mittal
Department of Mathematics, Indian Institute of Technology, Roorkee, India
Email: abelhaim@gmail.com, mittalrc@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 5 November 2013; revised 5 December 2013; accepted 16 December 2013
ABSTRACT
In this work, by extending the method of Hockney into three dimensions, the Poisson’s
equation in cylindrical coordinates system with the Dirichlet’s boundary conditions
in a portion of a cylinder for
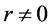 is solved directly. The Poisson equation is approximated by fourth-order finite
differences and the resulting large algebraic system of linear equations is treated
systematically in order to get a block tri-diagonal system. The accuracy of this
method is tested for some Poisson’s equations with known analytical solutions and
the numerical results obtained show that the method produces accurate results.
is solved directly. The Poisson equation is approximated by fourth-order finite
differences and the resulting large algebraic system of linear equations is treated
systematically in order to get a block tri-diagonal system. The accuracy of this
method is tested for some Poisson’s equations with known analytical solutions and
the numerical results obtained show that the method produces accurate results.
Keywords:Poisson’s Equation; Tri-Diagonal Matrix; Fourth-Order Finite Difference Approximation; Hockney’s Method; Thomas Algorithm

1. Introduction
The three-dimensional Poisson’s equation in cylindrical coordinates
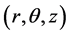 is given by
is given by
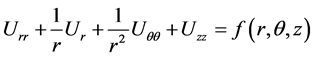 (1)
(1)
has a wide range of application in engineering and science fields (especially in physics).
In physical problems that involve a cylindrical surface (for example, the problem of evaluating the temperature in a cylindrical rod), it will be convenient to make use of cylindrical coordinates. For the numerical solution of the three dimensional Poisson’s equation in cylindrical coordinates system, several attempts have been made in particular for physical problems that are related directly or indirectly to this equation. For instance, Lai [1] developed a simple compact fourth-order Poisson solver on polar geometry based on the truncated Fourier series expansion, where the differential equations of the Fourier coefficients are solved by the compact fourth-order finite difference scheme; Mittal and Gahlaut [2] have developed high order finite difference schemes of secondand fourthorder in polar coordinates using a direct method similar to Hockney’s method; Mittal and Gahlaut [3] developed a secondand fourth-order finite difference scheme to solve Poisson’s equation in the case of cylindrical symmetry; Alemayehu and Mittal [4] have derived a second-order finite difference approximation scheme to solve the three dimensional Poisson’s equation in cylindrical coordinates by extending Hockney’s method; Tan [5] developed a spectrally accurate solution for the three dimensional Poisson’s equation and Helmholtz’s equation using Chebyshev series and Fourier series for a simple domain in a cylindrical coordinate system; Iyengar and Manohar [6] derived fourth-order difference schemes for the solution of the Poisson equation which occurs in problems of heat transfer; Iyengar and Goyal [7] developed a multigrid method in cylindrical coordinates system; Lai and Tseng [8] have developed a fourth-order compact scheme, and their scheme relies on the truncated Fourier series expansion, where the partial differential equations of Fourier coefficients are solved by a formally fourth-order accurate compact difference discretization. The need to obtain the best solution for the three dimensional Poisson’s equation in cylindrical coordinates system is still in progress.
In this paper, we develop a fourth-order finite difference approximation scheme and solve the resulting large algebraic system of linear equations systematically using block tridiagonal system [9] [10] and extend the Hockney’s method [9] [11] to solve the three dimensional Poisson’s equation on Cylindrical coordinates system.
2. Finite Difference Approximation
Consider the three dimensional Poisson’s equation in cylindrical coordinates
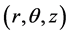 given by
given by
and the boundary condition
 (2)
(2)
where
![]() is the boundary of
is the boundary of
![]() and
and
![]() is
is
 and
and
Consider figure 1 as the geometry of the problem.
Let
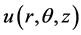 be discretized at the point
be discretized at the point
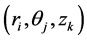 and for simplicity write a point
and for simplicity write a point
 as
as
 and
and
 as
as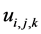 .
.
Assume that there are M points in the direction of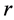 , N points in
, N points in
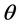 and P points in the
and P points in the
 directions to form the mesh, and let the step size along the direction of
directions to form the mesh, and let the step size along the direction of
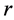 be
be![]() , of
, of
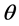 be
be
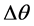 and
and
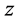 be
be![]() .
.
Here
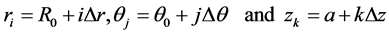
Where
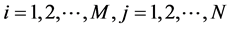 and
and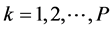 .
.
When
 is an interior or a boundary point of (2), then the Poisson’s equation becomes singular
and to take care of the singularity a different approach will be taken. Thus in
this paper we consider only for the case
is an interior or a boundary point of (2), then the Poisson’s equation becomes singular
and to take care of the singularity a different approach will be taken. Thus in
this paper we consider only for the case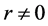 .
.
Using the approximations that
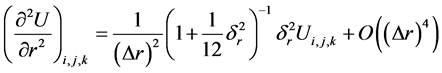 (3)
(3)
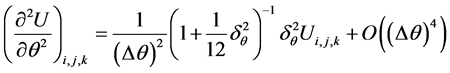 (4)
(4)

Figure 1. Portion of a cylinder.
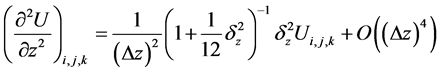 (5)
(5)
Now using (3), (4) and (5), we get (Refer the work of Mittal and Ghalaut in [2] )
From (1) consider only the approximation of the sum of the first and the third terms, that is, the sum of
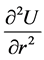 and
and
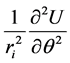
 (6)
(6)
where
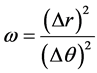
Again from (1) consider only the approximation of the sum of the first and the fourth terms, that is, the sum of
 and
and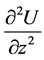 , and we get
, and we get
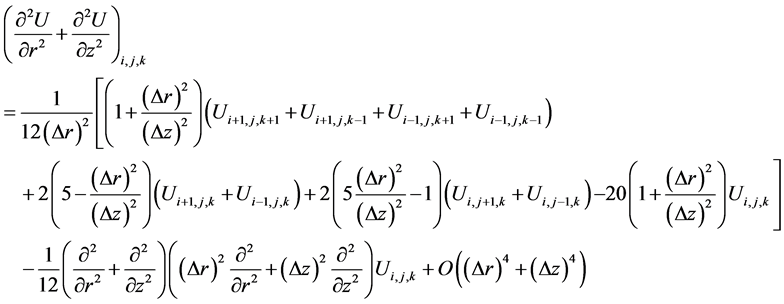 (7)
(7)
Once again from (1) consider only the approximation of the sum of the second and
the fourth terms, that is, the sum of
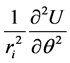 and
and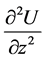 ; to get
; to get
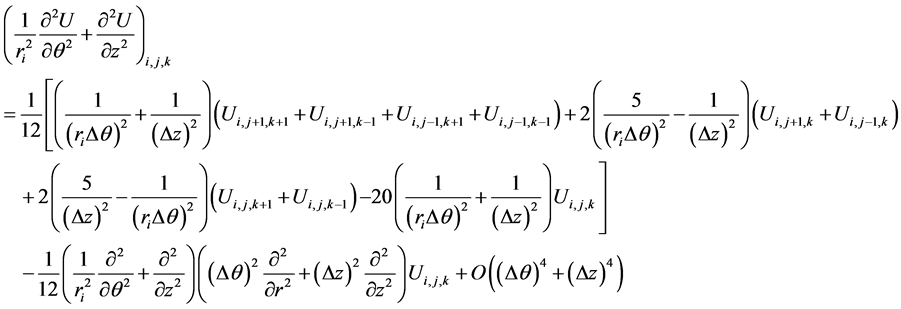 (8)
(8)
Again taking the approximation of the term
 by
by
 (9)
(9)
Equation (9) implying that
 (10)
(10)
Now letting
 and adding (6), (7), (8) and twice of (10), we get
and adding (6), (7), (8) and twice of (10), we get
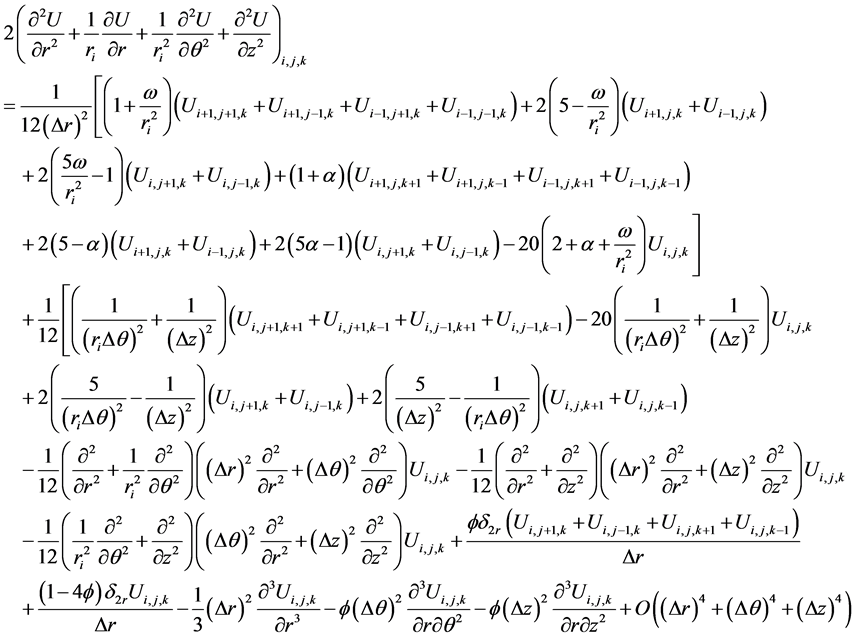 (11)
(11)
Now choose
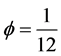 and consider the following terms in (11)
and consider the following terms in (11)
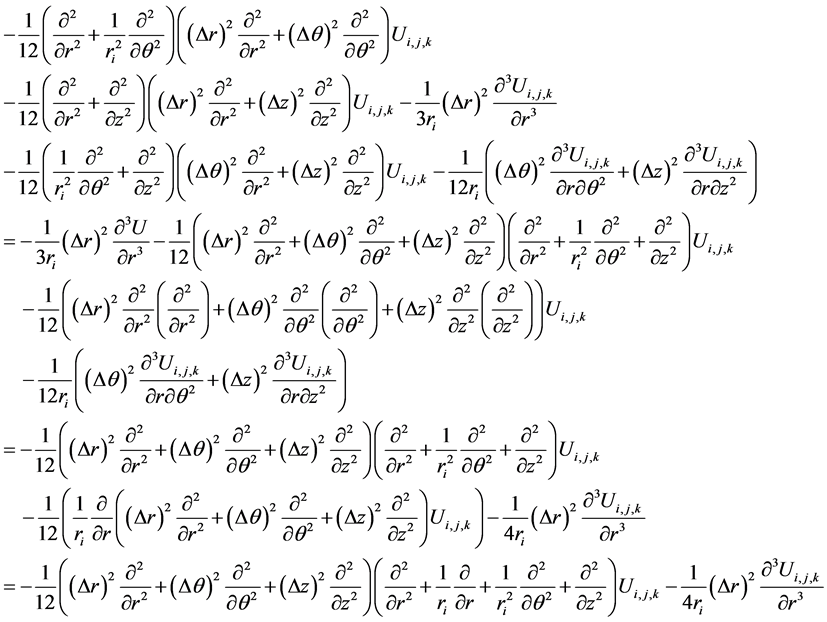 (12)
(12)
Again we can write the term
 in (12) as
in (12) as
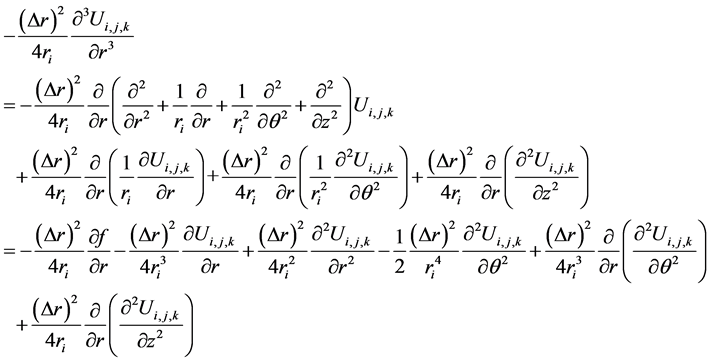 (13)
(13)
Using (12), (13), and multiplying both sides of (11) by
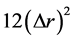 and rearranging and simplifying further, we get
and rearranging and simplifying further, we get
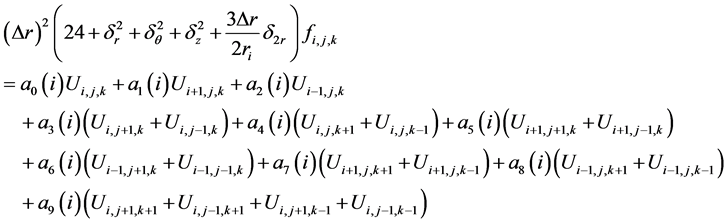 (14)
(14)
where
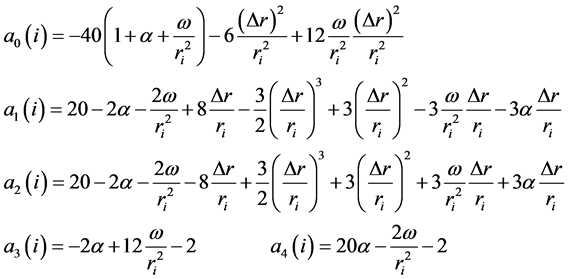
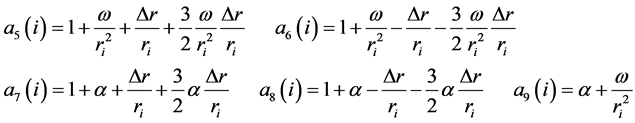
The system of equations in (14) is a linear sparse system, and thereby when solving we save both work and storage compared with a general system of equations. Such savings are basically true of finite difference methods: they yield sparse systems because each equation involves only few variables.
To solve equation (14), consider first in the
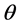 direction, next in the
direction, next in the
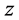 direction and lastly in the
direction and lastly in the
 direction, and thus (14) can be written in matrix form as
direction, and thus (14) can be written in matrix form as
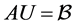 (15)
(15)
where
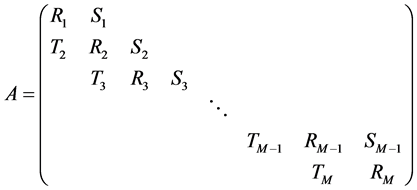
and it has
![]() blocks and each is of order
blocks and each is of order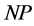 .
.
 ,
,
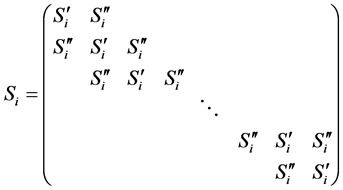
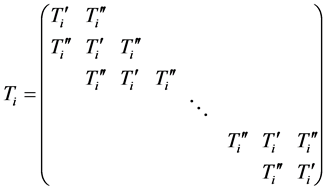
 are of order
are of order .
.
For the domain
![]()
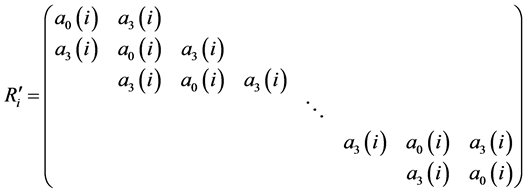
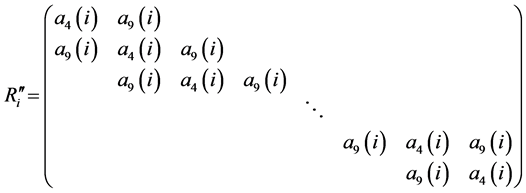
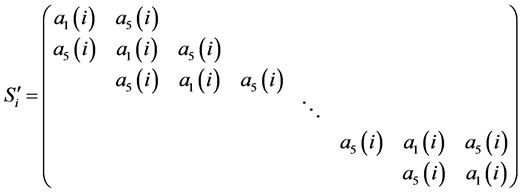
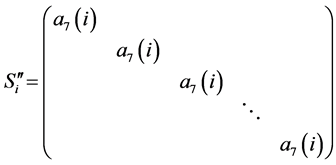 ,
,
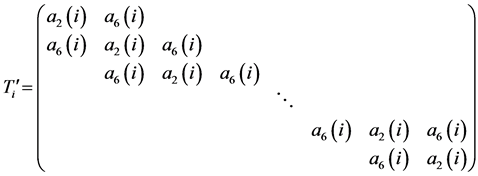

For the domain![]() ,
,
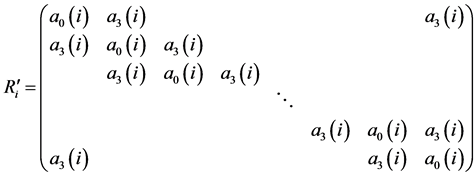


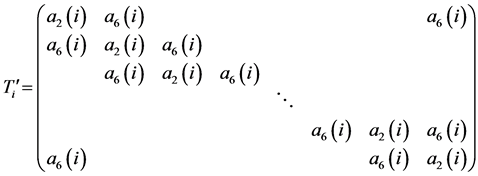
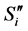 and
and
 are the same as in the domain
are the same as in the domain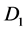 .
.
Here in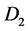 , the matrices
, the matrices
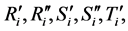 and
and
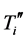 are circulant matrices of order
are circulant matrices of order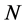 ; and
; and
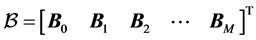 ,
,
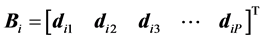 and
and
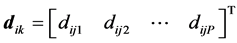
such that each
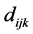 represents a known boundary values of
represents a known boundary values of
 and values of
and values of![]() , and
, and
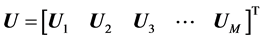 ,
,
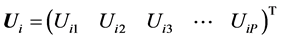 and
and
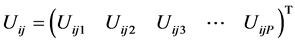
Thus, we write (15) as
 (16)
(16)
3. Extended Hockney’s Method
Observe that matrices
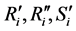 and
and
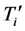 are real symmetric matrices and hence their eigenvalues and eigenvectors can easily
be obtained as
are real symmetric matrices and hence their eigenvalues and eigenvectors can easily
be obtained as
For
![]()
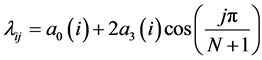 ,
,
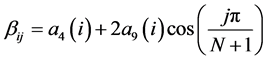 ,
,

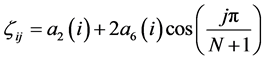 ,
,
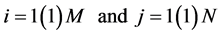
and for
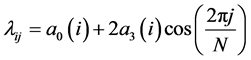 ,
,
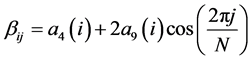 ,
,

 ,
,

Let
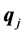 be an eigenvector of
be an eigenvector of
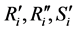 and
and
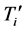 corresponding to the eigenvalue
corresponding to the eigenvalue
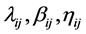 and
and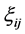 ; and matrix
; and matrix
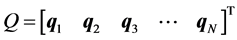 be a modal matrix of
be a modal matrix of
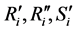 and
and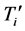 ,
,
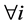 such that
such that
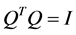
The
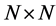 modal matrix Q is defined by
modal matrix Q is defined by
 ,
,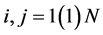 for
for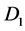 ;
;
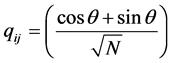 where
where
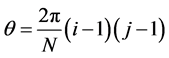
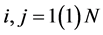 for
for
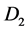
Let
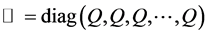 be a matrix of order
be a matrix of order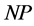 ; thus
; thus
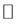 satisfy
satisfy
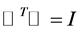 since
since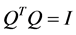 .
.
Since
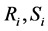 and
and
 are symmetric matrices, we have
are symmetric matrices, we have
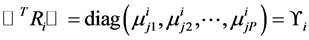 where
where

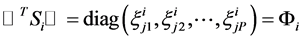 where
where
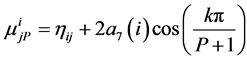
 where
where

Let
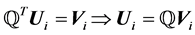 ,
,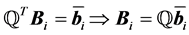 (17)
(17)
where
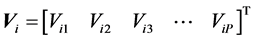 ,
,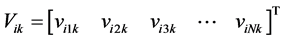 ;
;
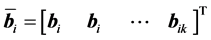 and
and
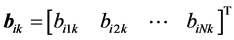
Pre-multiplying equation (16) by
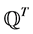 and applying (17), we get
and applying (17), we get
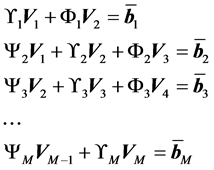 (18)
(18)
Now from each equation of (18) we collect the first equations and put them as one group of equation
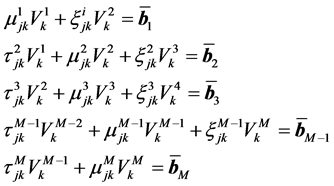 (19)
(19)
Now put
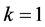 in equation (19) and collect the entire first set of equations, for
in equation (19) and collect the entire first set of equations, for
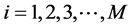 and
and
 to get
to get
![]() and
and
![]() (20a)
(20a)
Again consider the second equations by putting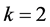 , and get
, and get
![]() and
and
![]() (20b)
(20b)
Continuing in this manner and finally considering the last equations for , we obtain
, we obtain
![]() and
and
![]() (20c)
(20c)
All these set of equations (20a)-(20c) are tri-diagonal ones and hence we solve
for
![]() by using Thomas algorithm. With the help of (17) again we get all
by using Thomas algorithm. With the help of (17) again we get all
![]() and this solves (14) as desired. By doing this we generally reduce the number of
computations and computational time.
and this solves (14) as desired. By doing this we generally reduce the number of
computations and computational time.
4. Numerical Results
In order to test the efficiency and adaptability of the proposed method, computational
experiments are done on some selected problems that may arise in practice, for which
the analytical solutions of
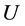 are known to us. The computed solutions are found for all grid points for any
values of
are known to us. The computed solutions are found for all grid points for any
values of
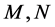 and
and![]() . Here results are reported at some randomly taken mesh
points in terms of the absolute maximum error from Table
1 to 7.
. Here results are reported at some randomly taken mesh
points in terms of the absolute maximum error from Table
1 to 7.
Example 1. Consider
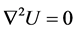 with the boundary conditions
with the boundary conditions ,
,

 , and
, and
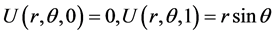
The analytical solution is
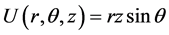 and the computed results of this example are shown in table
1.
and the computed results of this example are shown in table
1.
Example 2. Consider
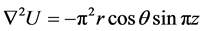 with the boundary conditions
with the boundary conditions
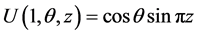 ,
,
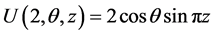
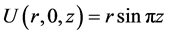 ,
,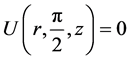 , and
, and
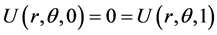
The analytical solution is
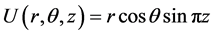 and the computed results of this example are shown in table
2.
and the computed results of this example are shown in table
2.
Example 3. Consider
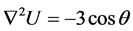 with the boundary conditions
with the boundary conditions
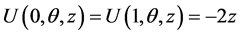 ,
,
 ,
,
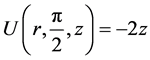
Table 1. Maximum absolute error of example 1.
Table 2. Maximum absolute error of example 2.
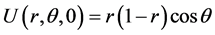 ,
,
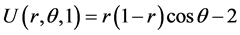
The analytical solution is
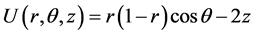 and the computed results of this example are shown in table
3.
and the computed results of this example are shown in table
3.
Example 4. Consider
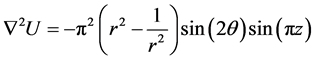 with the boundary conditions
with the boundary conditions
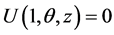 ,
,
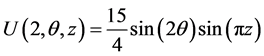 ,
,
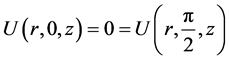 and
and
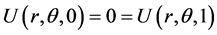
The analytical solution is
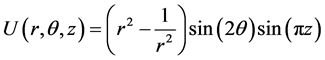 and the computed results of this example are shown in table
4.
and the computed results of this example are shown in table
4.
Example 5 Consider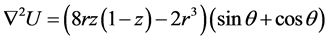 , where
, where
 with the boundary conditions
with the boundary conditions
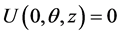 ,
,
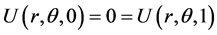
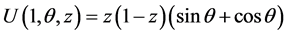
The analytical solution is
![]() and the computed results of this example are shown in Table
5.
and the computed results of this example are shown in Table
5.
Table 3. Maximum absolute error of example 3.
Table 4. Maximum absolute error of example 4.
Table 5. Maximum absolute error of example 5.
This example was considered by M.C. Lai [1] as a test problem and our results are better than their results in terms of accuracy. For instance, for (8,16,16) the maximum absolute error in their result is 9.1438e-004 and while ours is 3.28689e-004.
Example 6 Consider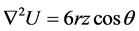 , where
, where
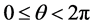 with the boundary conditions
with the boundary conditions
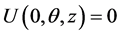 ,
,![]() ;
;
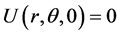 and
and
![]()
The analytical solution is
![]() and the computed results are shown in table 6.
and the computed results are shown in table 6.
Example 5.7 Consider
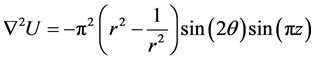 where
where
 with the boundary conditions
with the boundary conditions
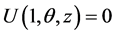 ,
,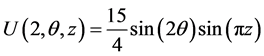 ;
;
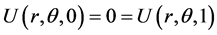
The analytical solution is
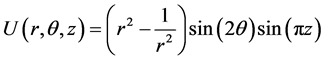 and the computed results of this example are shown in table
7.
and the computed results of this example are shown in table
7.
Table 6. Maximum absolute error of example 6.
Table 7. Maximum absolute error of example 7.
5. Conclusions
In this work, we have transformed the three dimensional Poisson’s equation in cylindrical coordinates system into a system of algebraic linear equations using its equivalent fourth-order finite difference approximation scheme. The resulting large number of algebraic equation is, then, systematically arranged in order to get a block matrix. By extending Hockney’s method to three dimensions, we reduced the obtained matrix into a block tridiagonal matrix, and each block is solved by the help of Thomas algorithm. We have successfully implemented this method to find the solution of the three dimensional Poisson’s equation in cylindrical coordinates system and it is found that the method can easily be applied and adapted to find a solution of some related applied problems. The method produced accurate results considering double precision. This method is direct and allows considerable savings in computer storage as well as execution speed.
Therefore, the method is suitable to apply to some three dimensional Poisson’s equations.
References
- Lai, M.C. (2002) A Simple Compact Fourth-Order Poisson Solver on Polar Geometry. Journal of Computational Physics, 182, 337-345. http://dx.doi.org/10.1006/jcph.2002.7172
- Mittal, R.C and Gahlaut, S. (1987) High Order Finite Difference Schemes to Solve Poisson’s Equation in Cylindrical Symmetry. Communications in Applied Numerical Methods, 3, 457-461.
- Mittal, R.C. and Gahlaut, S. (1991) High-Order Finite Differences Schemes to Solve Poisson’s Equation in Polar Coordinates. IMA Journal of Numerical Analysis, 11, 261-270. http://dx.doi.org/10.1093/imanum/11.2.261
- Alemayehu, S. and Mittal, R.C. (2013) Fast Finite Difference Solutions of the Three Dimensional Poisson’s Equation in Cylindrical Coordinates. American Journal of Computational Mathematics, 3, 356-361.
- Tan, C.S. (1985) Accurate Solution of Three Dimensional Poisson’s Equation in Cylindrical Coordinate by Expansion in Chebyshev Polynomials. Journal of Computational Physics, 59, 81-95. http://dx.doi.org/10.1016/0021-9991(85)90108-1
- Iyengar, S.R.K. and Manohar, R. (1988) High Order Difference Methods for Heat Equation in Polar Cylindrical Polar Cylindrical Coordinates. Journal of Computational Physics, 77, 425-438. http://dx.doi.org/10.1016/0021-9991(88)90176-3
- Iyengar, S.R.K. and Goyal, A. (1990) A Note on Multigrid for the Three-Dimensional Poisson Equation in Cylindrical Coordinates. Journal of Computational and Applied Mathematics, 33, 163-169. http://dx.doi.org/10.1016/0377-0427(90)90366-8
- Lai, M.C. and Tseng, J.M. (2007) A formally Fourth-Order Accurate Compact Scheme for 3D Poisson Equation in Cylindrical and Spherical Coordinates. Journal of Computational and Applied Mathematics, 201, 175-181. http://dx.doi.org/10.1016/j.cam.2006.02.011
- Smith, G.D. (1985) Numerical Solutions of Partial Differential Equations: Finite Difference Methods. Third Edition. Oxford University Press, New York.
- Malcolm, M.A. and Palmer, J. (1974) A Fast Method for Solving a Class of Tri-Diagonal Linear Systems. Communications of Association for Computing Machinery, 17, 14-17. http://dx.doi.org/10.1145/360767.360777
- Hockney, R.W. (1965) A Fast Direct Solution of Poisson Equation Using Fourier Analysis. Journal of Alternative and Complementary Medicine, 12, 95-113. http://dx.doi.org/10.1145/321250.321259


