American Journal of Computational Mathematics
Vol. 3 No. 2 (2013) , Article ID: 33538 , 6 pages DOI:10.4236/ajcm.2013.32017
On the Total Dynamic Response of Soil-Structure Interaction System in Time Domain Using Elastodynamic Infinite Elements with Scaling Modified Bessel Shape Functions
Structural Mechanic Department, VSU “L. Karavelov”, Sofia, Bulgaria
Email: kazakov@vsu.bg
Copyright © 2013 Konstantin Kazakov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 19, 2013; revised February 28, 2013; accepted March 30, 2013
Keywords: Soil-Structure Interaction; Wave Propagation; Infinite Elements; Finite Element Method; Bessel Functions; Duhamel Integral
ABSTRACT
This paper is devoted to a new approach—the dynamic response of Soil-Structure System (SSS), the far field of which is discretized by decay or mapped elastodynamic infinite elements, based on scaling modified Bessel shape functions are to be calculated. These elements are appropriate for Soil-Structure Interaction problems, solved in time or frequency domain and can be treated as a new form of the recently proposed elastodynamic infinite elements with united shape functions (EIEUSF) infinite elements. Here the time domain form of the equations of motion is demonstrated and used in the numerical example. In the paper only the formulation of 2D horizontal type infinite elements (HIE) is used, but by similar techniques 2D vertical (VIE) and 2D corner (CIE) infinite elements can also be added. Continuity along the artificial boundary (the line between finite and infinite elements) is discussed as well and the application of the proposed elastodynamical infinite elements in the Finite element method is explained in brief. A numerical example shows the computational efficiency and accuracy of the proposed infinite elements, based on scaling Bessel shape functions.
2. Elastodynamical Infinite Element with United Bessel Shape Functions
The idea and concept of the elastodynamic infinite elements with united shape functions (for short EIEUSF class infinite elements) are presented in [20,21]. Several EIEUSF formulations are discussed and have been demonstrated that the shape functions, related to nodes k and l (the nodes, situated in infinity, Figure 1, are not necessary to be constructed, because corresponding to these shape functions generalized coordinates or weights, see Equation (1), are zeros). The displacements in infinity are vanished, and these shape functions must be omitted. The theory used for the formulation of the EIEUSF class infinite elements has been published in detail in [6], and hence only summarize of the basic idea is demonstrated here. In [20] is mentioned why the EIEUSF class infinite elements are more general and powerful than the standard infinite elements.
The displacement field in the elastodynamical infinite
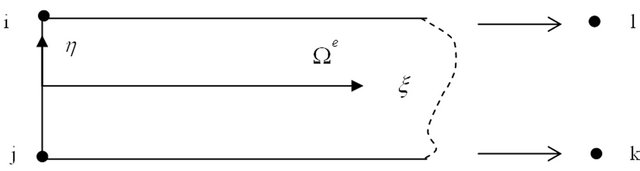
Figure 1. Local coordinate system of horizontal infinite elements (HIE).
element can be described in the standard form of the shape functions based on wave propagation functions as
 (1)
(1)
where 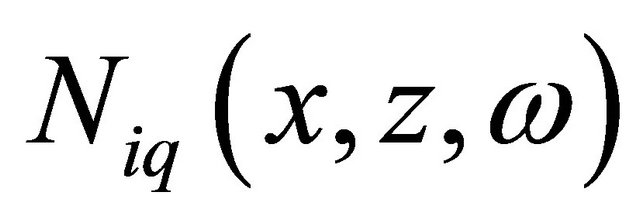 are the standard shape displacement functions,
are the standard shape displacement functions,  is the generalized coordinate associated with
is the generalized coordinate associated with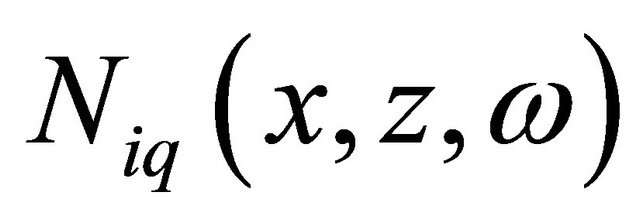 , n is the number of nodes for the element and m is the number of wave functions included in the formulation of the infinite element. For horizontal wave propagation basic shape functions for the HIE infinite element, the local coordinate system of which is shown in Figure 1, can be expressed as:
, n is the number of nodes for the element and m is the number of wave functions included in the formulation of the infinite element. For horizontal wave propagation basic shape functions for the HIE infinite element, the local coordinate system of which is shown in Figure 1, can be expressed as:
 (2)
(2)
where 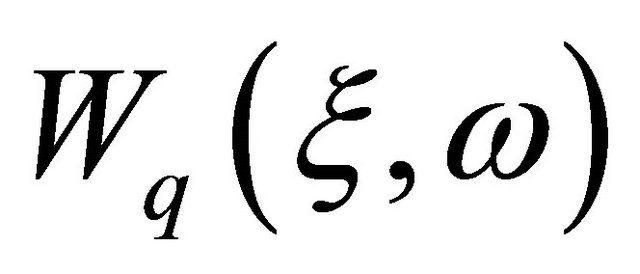 are horizontal wave functions and
are horizontal wave functions and 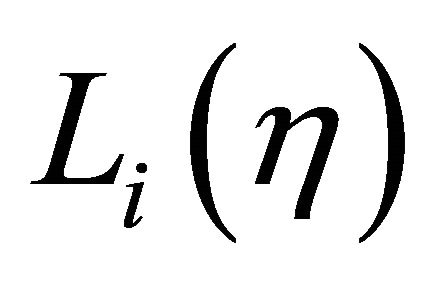 are Lagrange interpolation polynomial which has unit value at i-th node while zeros at the other nodes. For HIE infinite element the ranges of the local coordinates are:
are Lagrange interpolation polynomial which has unit value at i-th node while zeros at the other nodes. For HIE infinite element the ranges of the local coordinates are: 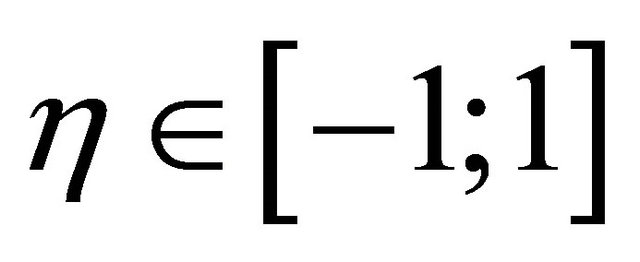 and
and . Here
. Here  assures the geometrical transformations of local to global coordinates.
assures the geometrical transformations of local to global coordinates.
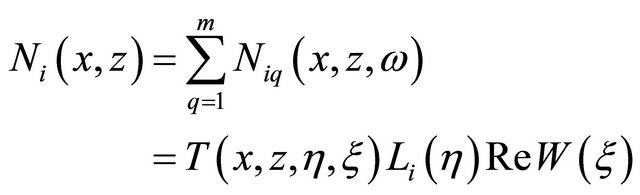 (3)
(3)
and
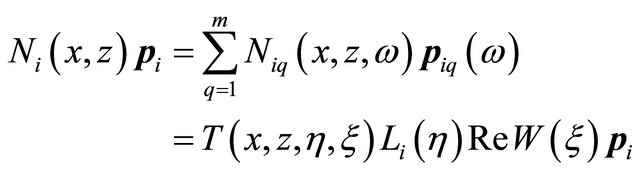 (4)
(4)
Then Equation (1) can be expressed as
 (5)
(5)
For horizontal wave propagation the basic shape functions for the HIE infinite element can be expressed using Bessel functions as follows:
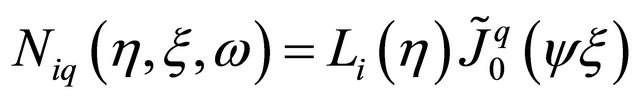 (6)
(6)
where 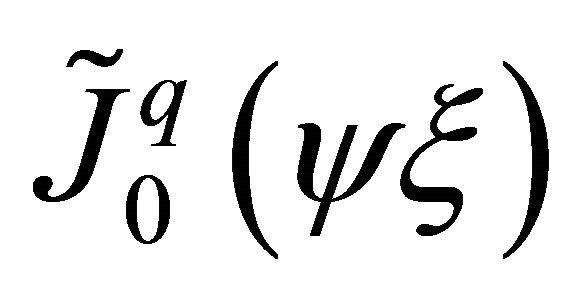 are scaling modified Bessel functions of first kind. These functions can be written as
are scaling modified Bessel functions of first kind. These functions can be written as
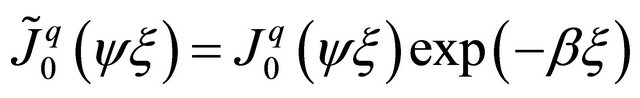 (7)
(7)
where 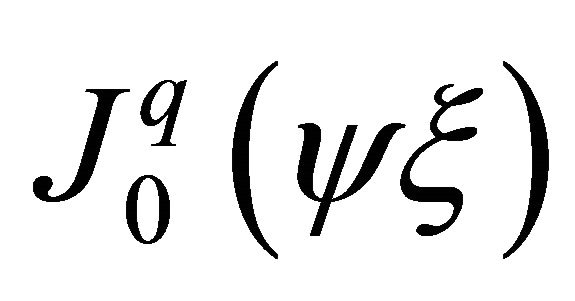 are standard Bessel functions of first kind. In Equations (6) and (7)
are standard Bessel functions of first kind. In Equations (6) and (7)  and
and  are constants, chosen in such a way that the length of the wave and the attenuation of the wave respectively, are identical with those, if Equation (2) is used. This means that the following two relations are valid:
are constants, chosen in such a way that the length of the wave and the attenuation of the wave respectively, are identical with those, if Equation (2) is used. This means that the following two relations are valid:
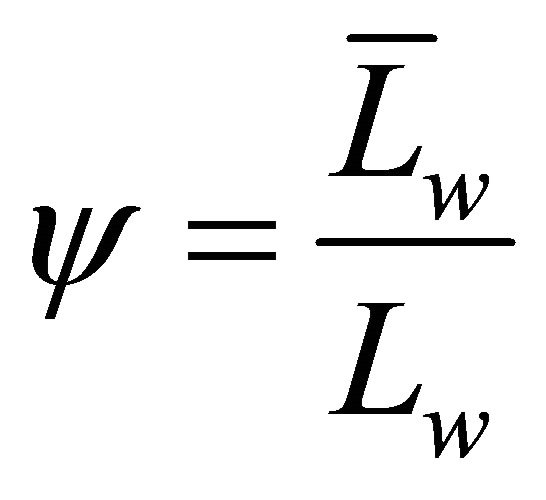 or
or  (8)
(8)
where  is the wave length if
is the wave length if  functions are used; π-if Bessel functions of first kind
functions are used; π-if Bessel functions of first kind  are used (average distance between two zeros) to approximate the displacements in the infinite element domain, and:
are used (average distance between two zeros) to approximate the displacements in the infinite element domain, and:
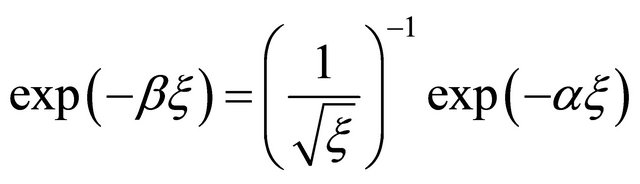 (9)
(9)
because the Bessel functions of first kind attenuate proportionally to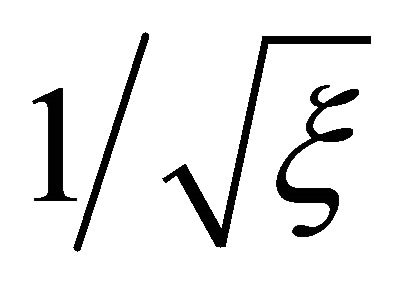 . The zeros of Bessel functions play a dominant role in applications of these functions [23] and demonstrate their oscillatory. Although the roots of Bessel functions are not generally periodic, except asymptotically for large
. The zeros of Bessel functions play a dominant role in applications of these functions [23] and demonstrate their oscillatory. Although the roots of Bessel functions are not generally periodic, except asymptotically for large , such functions give acceptable results for simulation of wave propagation. And what is more, using Bessel functions one can approximate change of the wave length in the far field region. If the element has four nodes and eight DOF (the simplest twodimensional plane element [6]) only four shape functions can be used to approximate the displacements, related to one frequency. These functions can be written as:
, such functions give acceptable results for simulation of wave propagation. And what is more, using Bessel functions one can approximate change of the wave length in the far field region. If the element has four nodes and eight DOF (the simplest twodimensional plane element [6]) only four shape functions can be used to approximate the displacements, related to one frequency. These functions can be written as:
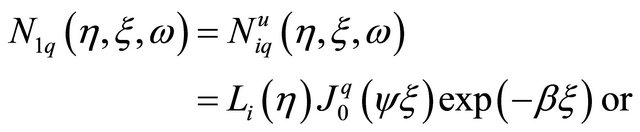 (10.a)
(10.a)
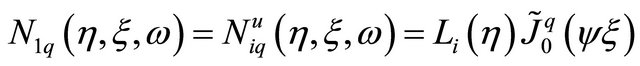 (10.b)
(10.b)
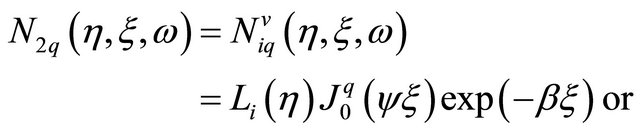 (11.a)
(11.a)
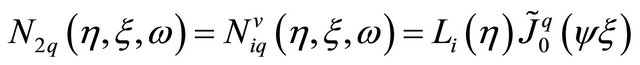 (11.b)
(11.b)
and
 (12.a)
(12.a)
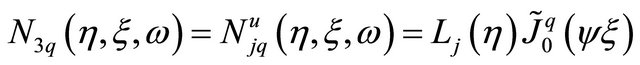 (12.b)
(12.b)
 (13.a)
(13.a)
 (13.b)
(13.b)
where in the general case .
.
If rotational DOF are used then the element has four nodes and 1o DOF. Two additional shape functions must be used, written as:
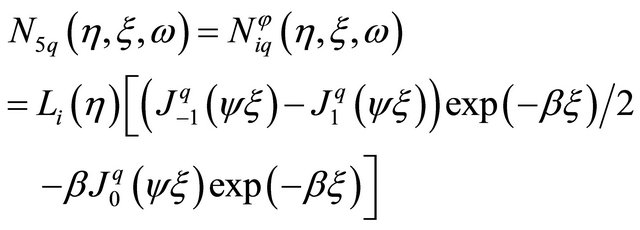 (14)
(14)
and
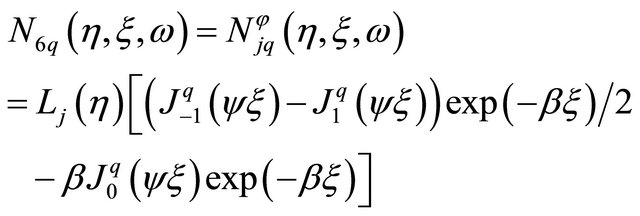 (15)
(15)
Here 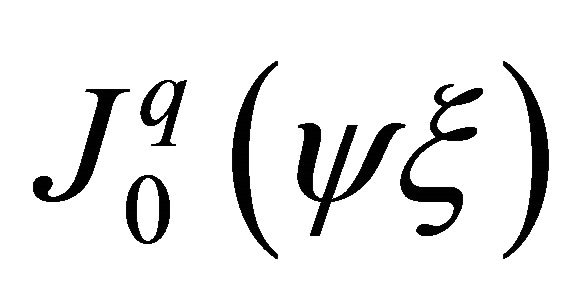 and
and 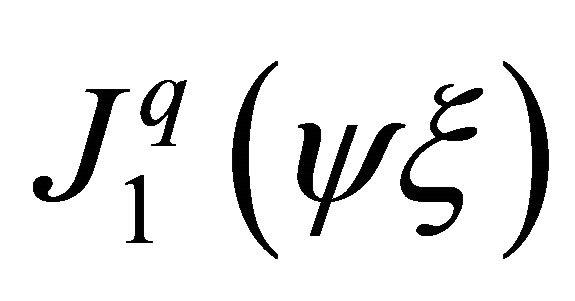 are Bessel functions of first kind.
are Bessel functions of first kind.
The function 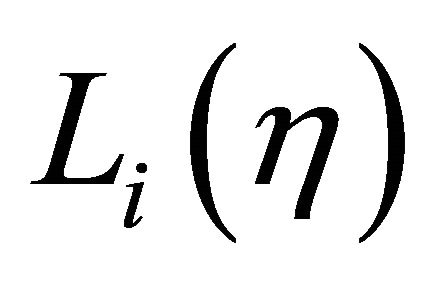 is linear if no mid-nodes. Finally, if mid-node on the side i-j is used, then the Lagrange interpolation polynomials must be quadratic. Scaling modified Bessel functions of first kind, in accordance with Equation (6) (
is linear if no mid-nodes. Finally, if mid-node on the side i-j is used, then the Lagrange interpolation polynomials must be quadratic. Scaling modified Bessel functions of first kind, in accordance with Equation (6) (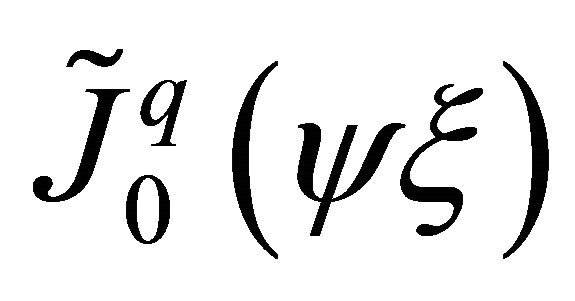 and
and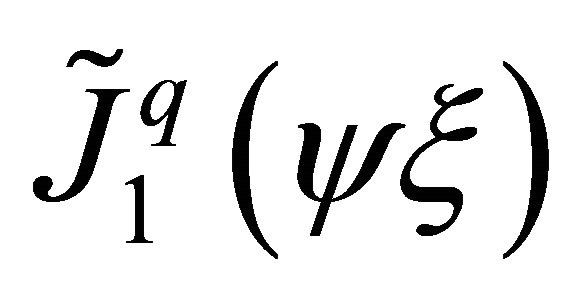 ), are illustrated in Figure 2.
), are illustrated in Figure 2.
The continuity along the artificial boundary (the line between finite and infinite elements, see Figure 3 line  and line
and line ) is assured in the same way as between two plane finite elements [21]. The application of the proposed infinite elements in the Finite element method is discussed below.
) is assured in the same way as between two plane finite elements [21]. The application of the proposed infinite elements in the Finite element method is discussed below.
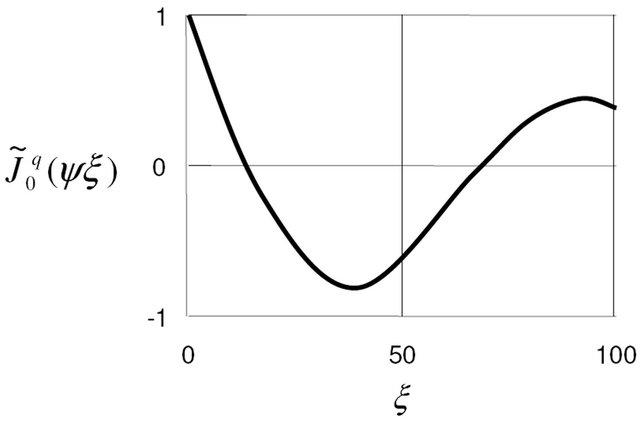
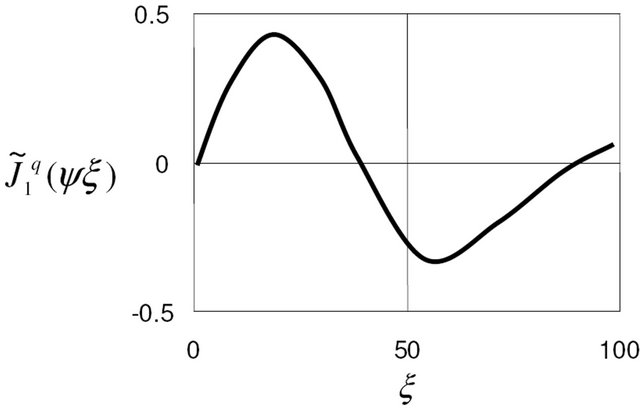
Figure 2. 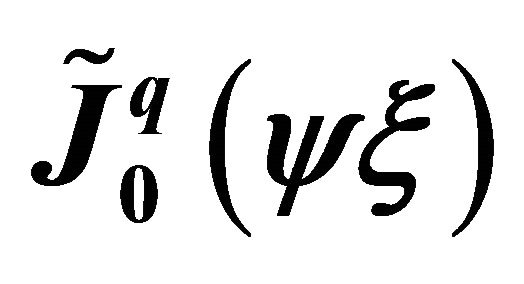 and
and  scaling modified Bessel functions.
scaling modified Bessel functions.

Figure 3. Computational model.
Using the procedure, given in details in [6] and briefly described here, mapped EIEUSF infinite elements, based on scaling modified Bessel functions, can be formulated, based on Equation (16)
 (16)
(16)
where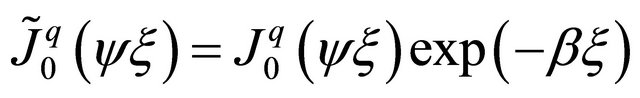 .
.
3. Stiffness and Mass Matrices
The matrices  and
and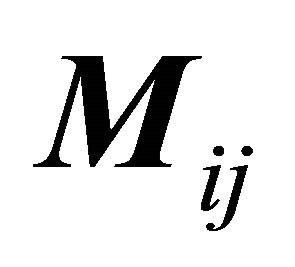 , related to the near field of the Soil-Structure System (SSS) can be written as
, related to the near field of the Soil-Structure System (SSS) can be written as
 (17)
(17)
and
 (18)
(18)
and those related to the far field  and
and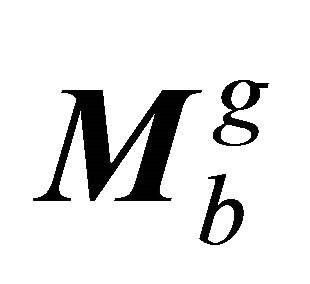 , i.e. obtained for the proposed infinite elements, as
, i.e. obtained for the proposed infinite elements, as
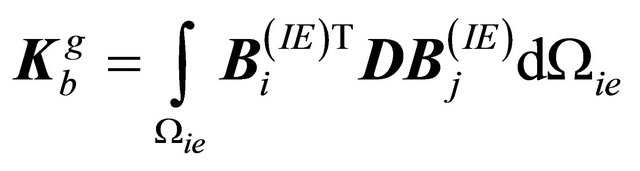 (19)
(19)
and
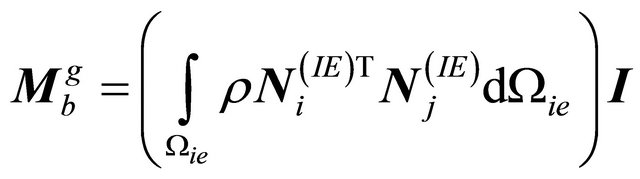 (20)
(20)
where N, B and D are shape function matrix, strain-displacement matrix and stress-strain matrix, respectively.
The matrices  and
and 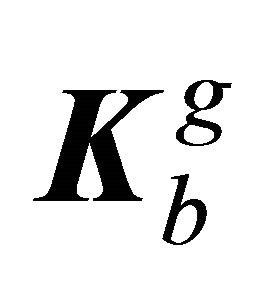 are calculated using the principle of the virtual work.
are calculated using the principle of the virtual work.
If Bessel functions are used, the first derivative of 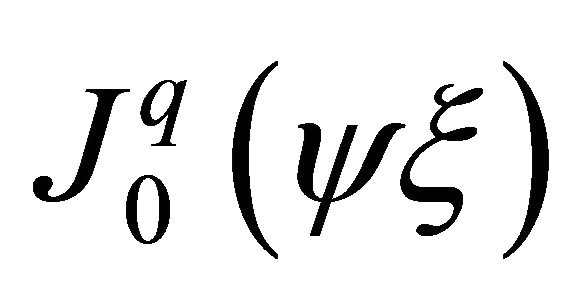 (The Taylor series indicate that by
(The Taylor series indicate that by 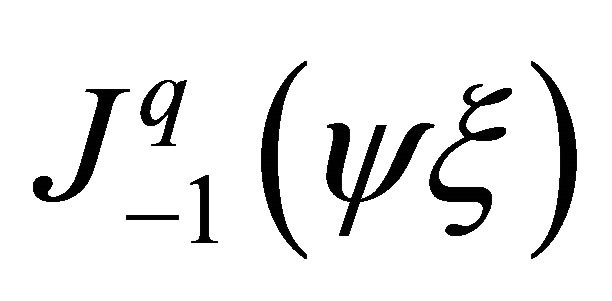 and
and 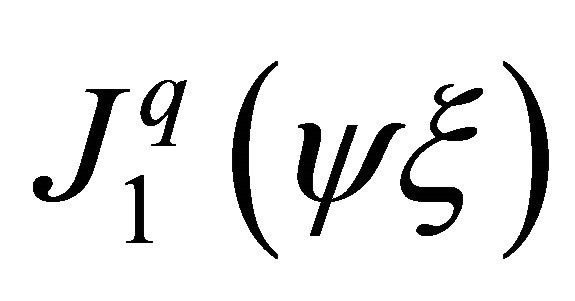 the derivative of
the derivative of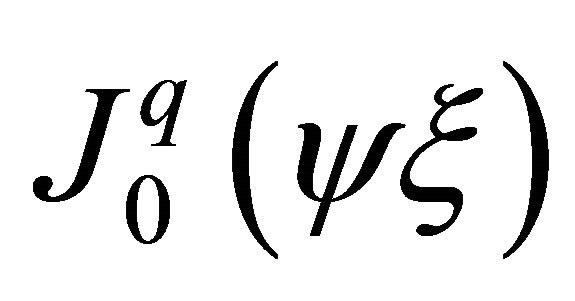 ) can be expressed) is
) can be expressed) is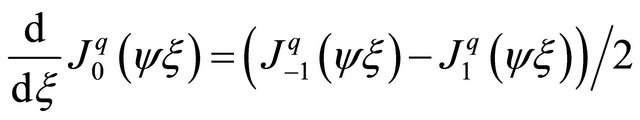 .
.
The general form of the equations of motion in time domain can be written as
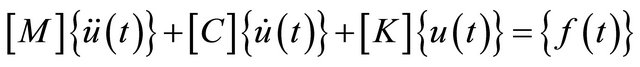 (21)
(21)
where 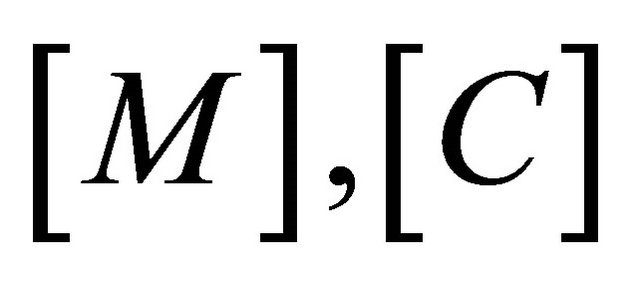 and
and  are mass, damping and stiffness matrices, respectively, and
are mass, damping and stiffness matrices, respectively, and 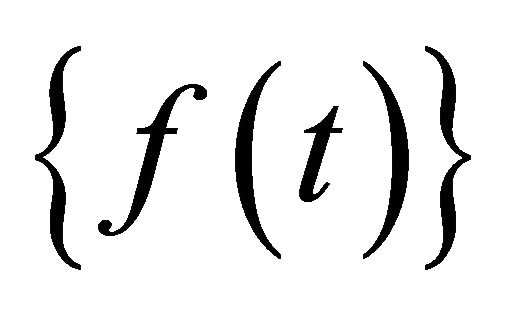 is nodal force vector.
is nodal force vector.
The equations of motion of the entire SSS, using the Substructural approach with EIEUSF infinite elements, based on scaling modified Bessel functions, transformed into time domain by inverse Fourier transformation, are
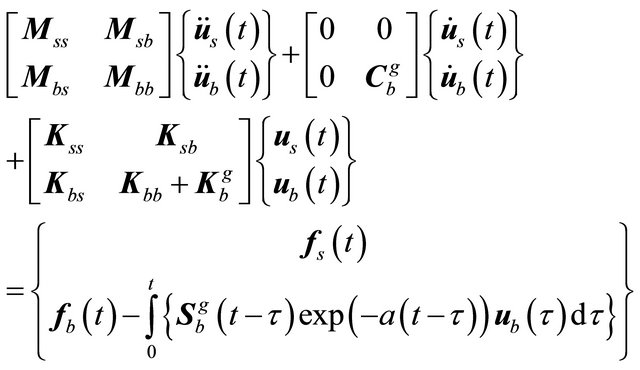 (22)
(22)
if massless far field is assumed. In Equation (21) 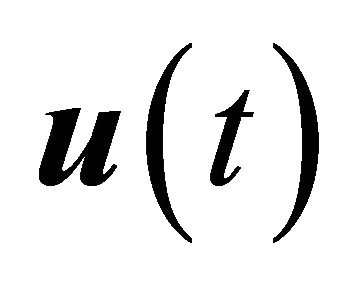 and
and 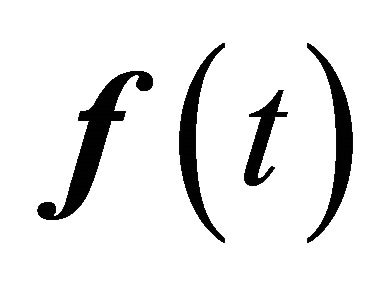 are respectively displacement and force vectors, and
are respectively displacement and force vectors, and  and
and  are matrices of mechanical characteristics of the far field soil region. Here
are matrices of mechanical characteristics of the far field soil region. Here
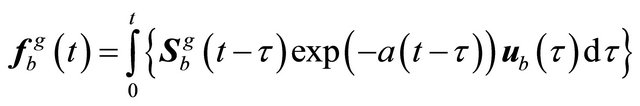 (23)
(23)
can be assumed as a Duhamel integral or more generally as a convolution integral, for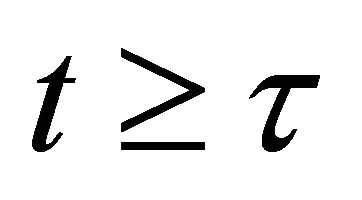 .
.
Equation (23) is a standard convolution of two functions, given in vector forms, namely 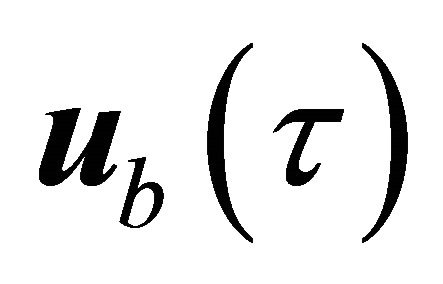 and
and . Here the vector components of
. Here the vector components of  can be taken in case of seismic events from seismograms.
can be taken in case of seismic events from seismograms.
If rotational acceleration of the base is possible, than Equation (22) becomes
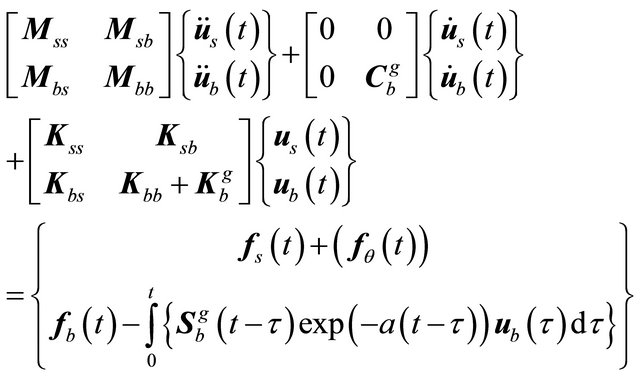 (24)
(24)
where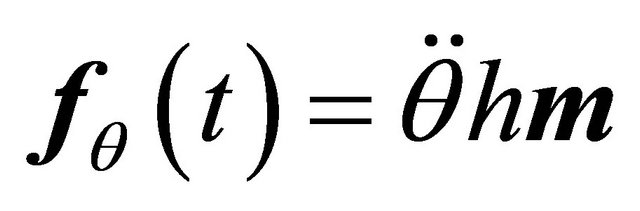 .
.
The matrix  assures the transformation of the nodal unit displacement impulse vector
assures the transformation of the nodal unit displacement impulse vector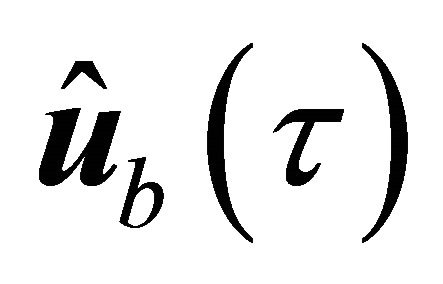 , applied at moment
, applied at moment , to a nodal force vector
, to a nodal force vector
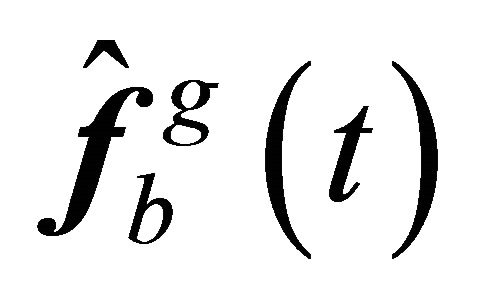 at moment
at moment  and can be treated as a transformation matrix, the general form of which can be written as
and can be treated as a transformation matrix, the general form of which can be written as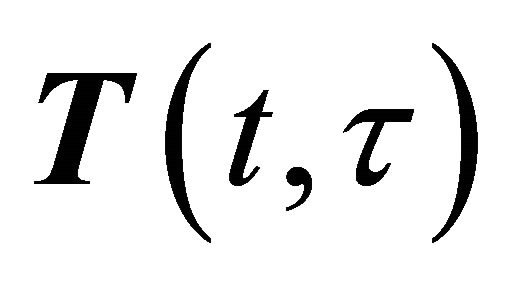 . This matrix in the present case can be expressed as
. This matrix in the present case can be expressed as
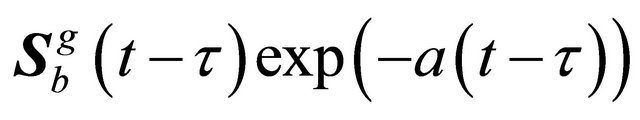 (25)
(25)
where 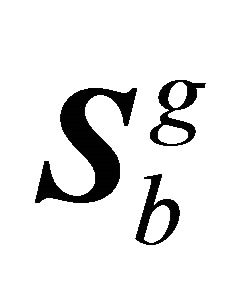 can be treated as a stiffness matrix, the components of which can be calculated from
can be treated as a stiffness matrix, the components of which can be calculated from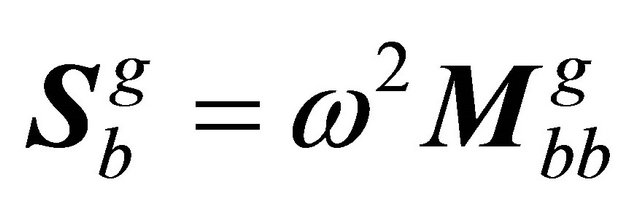 .
.
The vector 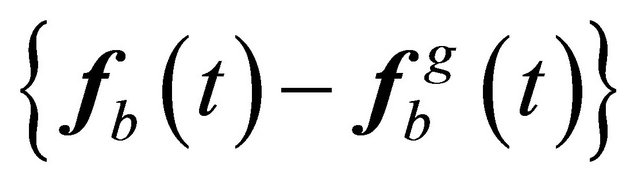 denotes the vector of interaction forces of the unbounded soil acting at nodes b, the nodes situated on the artifitual boundary. These forces are acting as a result of the relative motion between the unbounded soil and the total motion of the near field, see Figure 3, expressed in vector forms as
denotes the vector of interaction forces of the unbounded soil acting at nodes b, the nodes situated on the artifitual boundary. These forces are acting as a result of the relative motion between the unbounded soil and the total motion of the near field, see Figure 3, expressed in vector forms as  or
or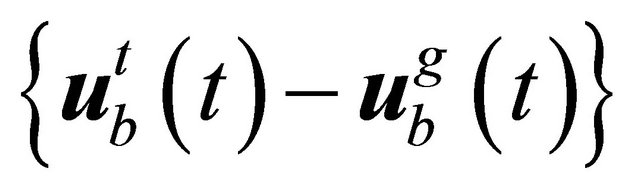 .
.
For discrete time points the vector 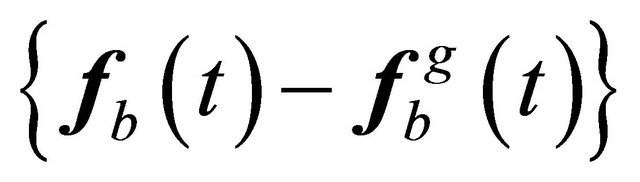 is calculated, using Equation (26) as
is calculated, using Equation (26) as
 (26)
(26)
If the force vector, i.e.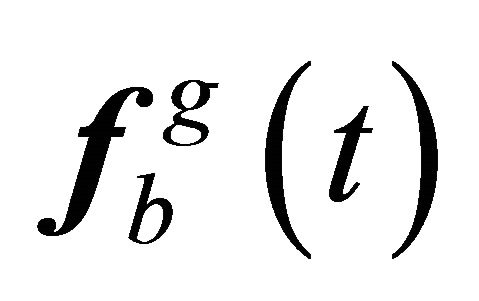 , at moment
, at moment  is known, i.e.
is known, i.e.
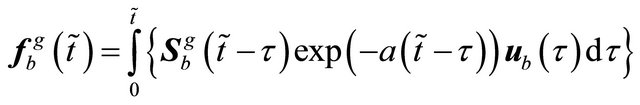 (27)
(27)
at moment , the force vector
, the force vector 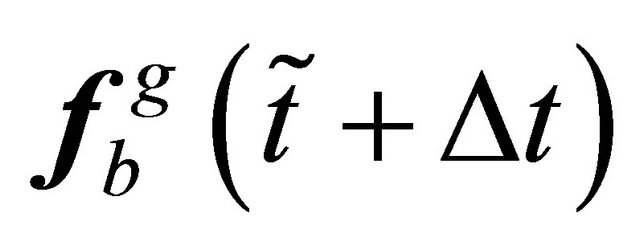 can be obtained using
can be obtained using
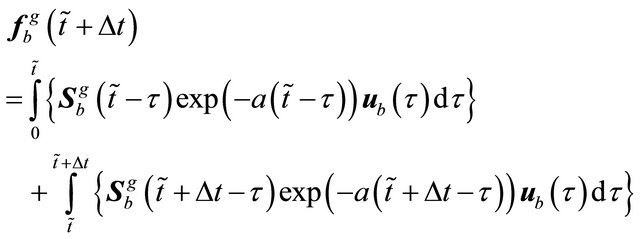 (28)
(28)
or if 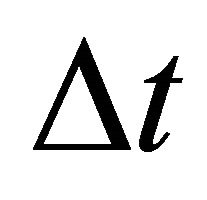 is small time interval using the approximation
is small time interval using the approximation
 (29)
(29)
If Equation (23) is expressed as
 (30)
(30)
then the trigonometric identity
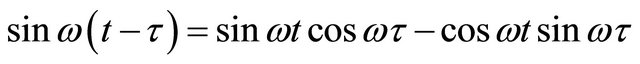
can be used and finally
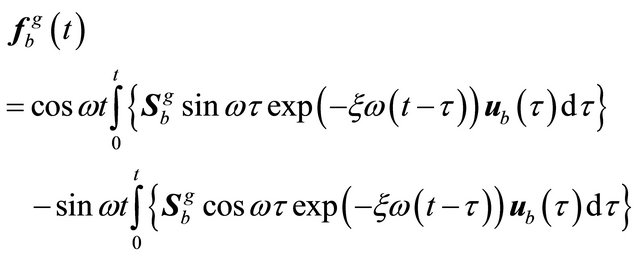 (31)
(31)
Using the proposed infinite elements, the resulting element stiffness matrices related to the far field are inexpensive to calculate and the global stiffness matrix has relatively small bandwidth. It is reasonable to expect similar results in SSI simulations, based on EIEUSF infinite elements with modified Bessel shape functions to those when EIEUSF infinite elements are used.
The nodal displacement vector at moment t can be calculated using step-by-step method, applied to Equation (23), given in time domain. Such a computational technology is demonstrated in the next Section.
4. Numerical Example
Structure with rigid strip foundation resting on a homogeneous half-space is modeled as shown in Figure 3, and the far field is descretized by elastic springs with stiffness  (model 1), by elastic springs with stiffness
(model 1), by elastic springs with stiffness 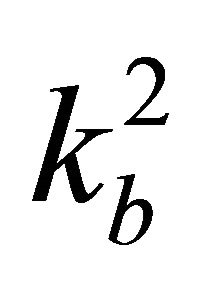 (model 2), by massless EIEUSF infinite elements with one wave frequency [20] (model 3) and by massless infinite elements with Bessel shape functions [20] (model 4).
(model 2), by massless EIEUSF infinite elements with one wave frequency [20] (model 3) and by massless infinite elements with Bessel shape functions [20] (model 4).
Horizontal harmonic displacements with period 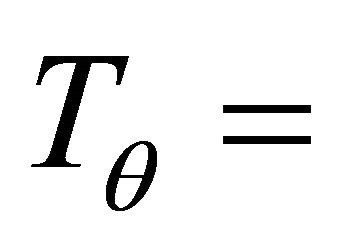
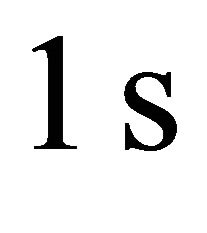 and amplitude
and amplitude 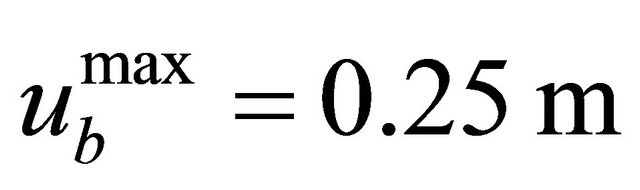 are applied on the nodes as shown in Figure 3. The geometry of the model and the material parameters are given in [6].
are applied on the nodes as shown in Figure 3. The geometry of the model and the material parameters are given in [6].
The results for the first 4 natural periods, corresponding to the models and max displacement of node S, are given in Table 1. The time history of the displacements of node S, see Figure 3, between 9.1 s and 9.5 s are illustrated in Figure 4.
The numerical example shows that, if EIEUSF infinite elements or infinite elements with Bessel shape functions are used, the position of  can be translated starting from
can be translated starting from 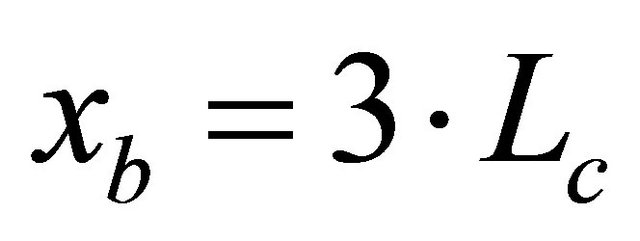 (see
(see  in Figure 3) to
in Figure 3) to  without significant influence on the results. However, if elastic springs are used, the results are significantly affected. Such a reduction of the near field demonstrates the effectiveness of the proposed infinite elements.
without significant influence on the results. However, if elastic springs are used, the results are significantly affected. Such a reduction of the near field demonstrates the effectiveness of the proposed infinite elements.
5. Conclusions
In this paper a formulation of elastodynamical infinite element, based on scaled Bessel shape functions, is appropriate for Soil-Structure Interaction problem, and the computational concept and the corresponding equations
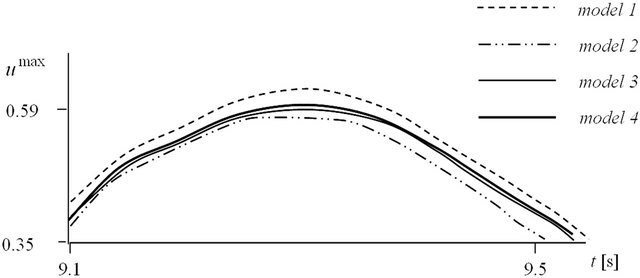
Figure 4. Time history of the displacements of node S.
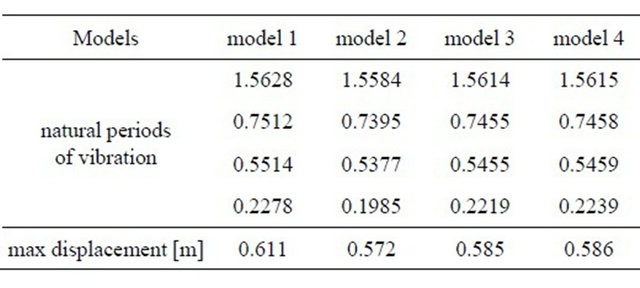
Table 1. Natural periods, corresponding to the models and max displacements of node S.
of motion of the entire SSI system are presented. This element is a new form of the infinite element, given in [6,21]. The base of the development is new shape functions, obtained by modification of the standard Bessel functions of first kind 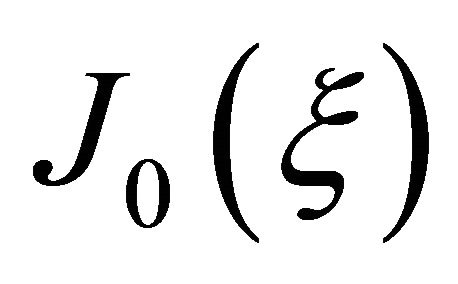 by appropriately chosen scale factor. The stiffness matrices of these infinite elements are calculated by EIEUSF matrix module, and developed by the same author.
by appropriately chosen scale factor. The stiffness matrices of these infinite elements are calculated by EIEUSF matrix module, and developed by the same author.
The numerical example shows the computational efficiency and accuracy of the proposed infinite elements. Such elements can be directly used in the FEM code. The results are in a good agreement with the results, obtained by EIEUSF infinite elements. Moreover, the use of scaling modified Bessel functions in the construction of the shape functions leads to computational efficiency in the stage of the calculation of the stiffness and mass infinite element coefficients.
The formulation of 2D horizontal type infinite elements (HIE) is demonstrated, but by similar techniques 2D vertical (VIE) and 2D corner (CIE) infinite elements can also be formulated. It was demonstrated that the application of the elastodynamical infinite elements is the easier and appropriate way to achieve an adequate simulation (2D elastic media) including basic aspects of SoilStructure Interaction. Continuity along the artificial boundary (the line between finite and infinite elements) is discussed as well and the application of the proposed elastodynamical infinite elements in the Finite element method is explained in brief.
REFERENCES
- D. Aubry, D. Clouteau and P. D’Azemar, “A Dynamic Substructure Approach to Soil-Structure Interaction,” Computational Mechanics Publications, Vol. 3, Springer Verlag, Berlin, 2002.
- K. J. Bathe, “Finite Element Procedures in Engineeringanalysis,” Prentice-Hill, Upper Saddle River, 1982.
- U. Basu and A. K. Chopra, “Numerical Evaluation of the Damping-Solvent Extraction Method in the Frequency Domain,” Earthquake Engineering and Structural Dynamics, Vol. 31, No. 6, 2002, pp. 1231-1250. doi:10.1002/eqe.156
- P. Bettess, “Infinite Elements,” International Journal for Numerical Methods in Engineering, Vol. 11, No. 1, 1978, pp. 54-64.
- K. Fang and R. Brown, “Numerical Simulation of Wave Propagation in Anisotropic Media,” CREWES Research Report, Vol. 7, 1995.
- K. S. Kazakov, “Elastodynamic Infinite Elements with United Shape Function for Soil-Structure Interaction,” Finite Elements in Analysis and Design, Vol. 46, No. 10, 2010, pp. 936-942. doi:10.1016/j.finel.2010.06.008
- J. E. Luco and R. A. Westmann, “Dynamic Response of a Rigid Footing Bonded to an Elastic Half Space,” Journal of Applied Mechanics, Vol. 39, No. 2, 1972, pp. 93-99. doi:10.1115/1.3422711
- S. P. G. Madabhushi, “Modeling of Deformations in Dynamic Soil-Structure Interaction Problems,” VELACS, Technical Report TR277, Cambridge University, Cambridge, 1996.
- H. S. Oh and Y. Ch. Jou, “The Weighted Riesz-Galerkin Method for Elliptic Boundary Value Problems on Unbounded Domain,” NC 28223-0001.
- K. S. Kazakov, “Infinite Elements in the Finite Element Method,” 3rd Edition, VSU Publishing House, Sofia, 2010.
- R. F. Ungless, “Infinite Elements,” M.Sc. Dissertation, University of British Columbia, Vancouver, 1973.
- J. P. Wolf and C. Song, “Finite-Element Modeling of Unbounded Media,” Wiley, London, 1996.
- M. C. Genes and S. Kocak, “A Combined Finite Element Based Soil-Structure Interaction Model for Large-Scale System and Applications on Parallel Platforms,” Engineering Structures, Vol. 24, No. 9, 2002, pp. 1119-1131. doi:10.1016/S0141-0296(02)00042-1
- K. S. Kazakov, “The Finite Element Method for Structural Modelling,” 2nd Edition, Bulgarian Academy of Science (BAS) Publishing House, Sofia, 2009.
- J. P. Wolf, “Soil-Structure Interaction Analysis in a Time Domain,” Prentice-Hill, Englewood Cliffs, 1988.
- Ch. B. Yan, D. K. Kim and J. N. Kim, “Analytical Frequency-Dependent Infinite Elements for Soil-Structure Interaction Analysis in a Two-Dimensional Medium,” Engineering Structures, Vol. 22, No. 3, 2000, pp. 258- 271. doi:10.1016/S0141-0296(98)00070-4
- Ch. Zhao and S. Valliappan, “A Dynamic Infinite Element for Three-Dimensional Infinite Domain Wave Problems,” International Journal for Numerical Methods in Engineering, Vol. 36, No. 15, 1993, pp. 2567-2580. doi:10.1002/nme.1620361505
- K. S. Kazakov, “Formulation of Elastodynamic Infinite Elements for Dynamic Soil-Structure Interaction,” WSEAS Transactions on Applied and Theoretical Mechanics, Vol. 6, No. 1, 2011, pp. 91-96.
- K. S. Kazakov, “Mapping Functions for 2D Elastodynamic Infinite Element with United Shape Function,” Slovak Journal of Civil Engineering, Vol. 16, 2008, pp. 17- 25.
- K. S. Kazakov, “On an Elastodynamic Infinite Element, Appropriate for an Soil-Structure Interaction Models,” Proceedings of 10th Jubilee National Congress on Theoretical and Applied Mechanics, Varna, Vol. 1, 2005, pp. 230-236.
- K. S. Kazakov, “Stiffness and Mass Matrices of FEMApplicable Dynamic Infinite Element with Unified Shape Basis,” AIP Conference Proceedings, Vol. 1138, No. 1, 2009, p. 95. doi:10.1063/1.3155133
- P. K. Pradhan, D. K. Baidya and D. P. Ghosh, “Impedance Functions of Circular Foundation Resting on Soil Using Cone Model,” ASME Report 12, 2003.
- F. E. Relton, “Applied Bessel Functions,” Blackie and Son, London, 1946.

